基于改進NSGA2算法的航空燃油泵葉輪優化設計

白永明，陶 藝，吳迎春，張小波，王宏建

(1.無錫工藝職業技術學院， 江蘇 宜興 214206; 2.中航工業金城南京機電液壓工程研究中心，南京 211102)

航空燃油泵是飛機燃油系統的重要附件，為發動機供、輸燃油，保障飛機安全運行。目前，我國飛機燃油系統的供、輸油所用的燃油泵大部分是離心式電動燃油泵。燃油泵的優化設計一直是個難題，因為它是一個多目標優化問題，涉及揚程、汽蝕余量和揚程駝峰等目標，這些目標是相互制約的，某個子目標性能的改善可能引起其他子目標性能的降低，不可能使所有子目標均達到最優的效果，如泵葉輪的優化設計中增大葉輪出口直徑能提高揚程但容易出現揚程駝峰。傳統設計方法在面臨如何確定取值范圍較大的各種參數的問題時，主要是基于大量的設計經驗，因此燃油泵性能的優劣很大程度上就取決于設計者的經驗和水平，而且需要經過多次“設計-試驗-改進-試驗”的循環，導致設計周期長，效率低，效果差。燃油泵的快速優化設計成為一個值得研究的課題，從以往的一些研究成果來看，優化變量一般只有2～3個，其他的參數仍由設計者根據經驗賦值，而且多為單目標優化或將多目標轉化為單目標后再進行優化求解的[1-2]。為了突破經驗約束并實現多目標同時優化，提高燃油泵的設計效率和性能，將多目標遺傳算法用于航空燃油泵的優化設計。

1 改進NSGA2算法

遺傳算法作為一種有效的尋優方法，為多目標優化問題的求解提供了一個新思路。遺傳算法是對整個群體進行進化運算操作，它著眼于個體的集合，而多目標優化問題的最優解也是一個集合，因而可以說遺傳算法是求解多目標優化問題的有效手段。目前比較典型的多目標遺傳算法有：向量評估遺傳算法(VEGA)、小生境Pareto遺傳算法(NPGA)、強度Pareto進化算法(SPEA)、非支配排序的遺傳算法(NSGA)和帶精英策略的非支配排序的遺傳算法(NSGA2)。

NSGA2算法操作簡單，具有較好的收斂速度和魯棒性好，已成為多目標優化領域的基準算法，在工程上有著良好的應用[3-5]。圖1為NSGA2算法優化流程，首先進行適值分配，然后按照適值分配得到的適應度選擇父代個體，對父代個體進行交義、變異操作，構成新一代子群。產生新一代種群后，重新計算種群中每個個體對應的目標函數值，判斷其是否滿足終止條件。如此循環往復，直至滿足終止條件。

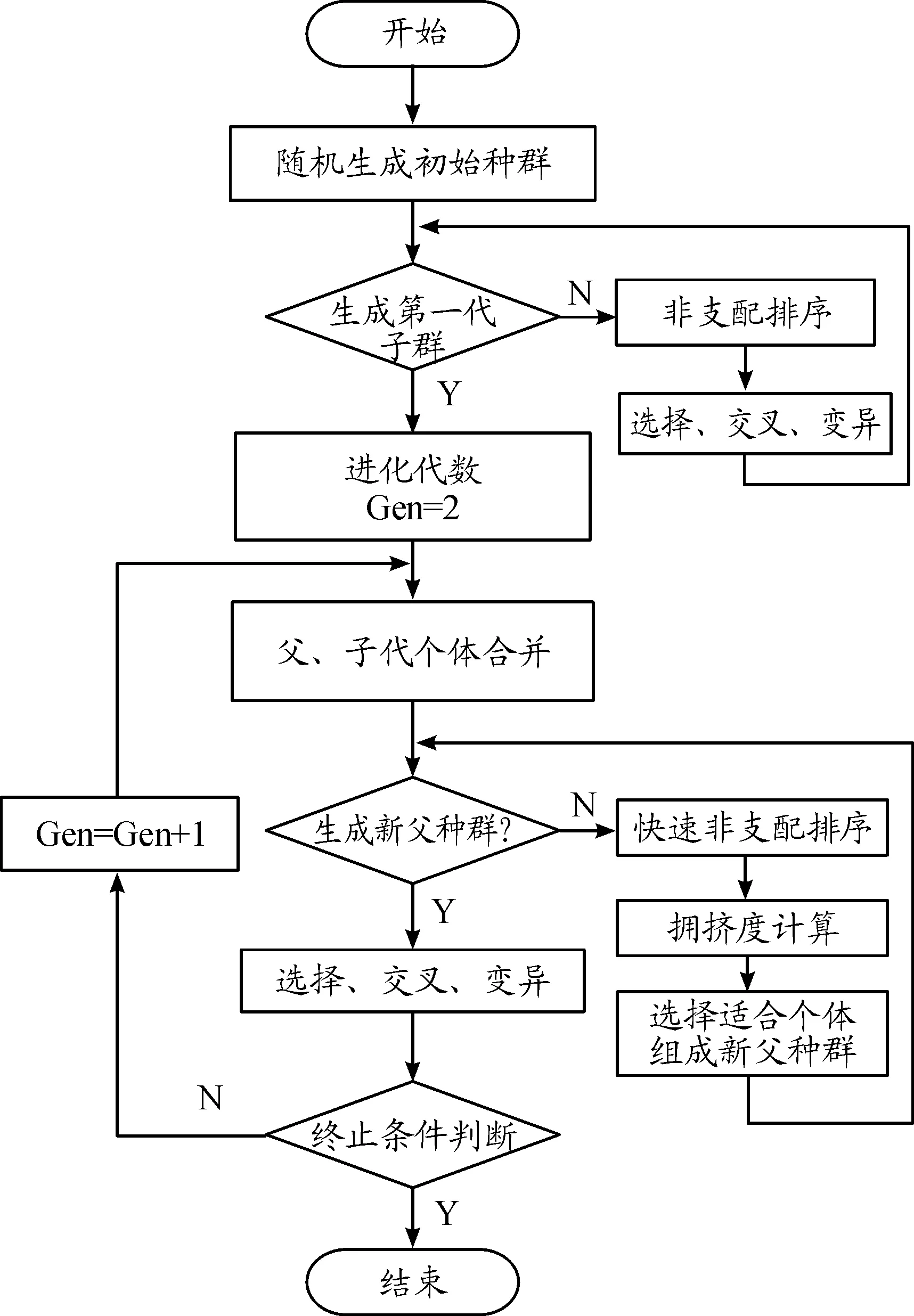
圖1 NSGA2算法優化流程框圖

但NSGA2算法在計算中也存在無法有效識別偽非支配解、計算效率低、解集收斂性和分布性較差等設計缺陷。針對前述的缺陷，對NSGA2算法進行相應改進[6-8]。

1.1 精英策略改進

NSGA2算法采用的精英保存策略和錦標賽選擇法，會使Pareto最優解層個體迅速繁殖，并使非支配層數目和其他非優支配層中的個體數目減少，使得側向多樣性損失嚴重，會導致局部收斂。因此將NSGA2算法的精英保存策略改為精英控制策略

(1)

式(1)中：Nj為第j個非支配層的最大個體數；N為種群大小；r∈[0，1]，為衰減率。

改進后，可對每一個非支配層中的最大個體數目進行約束，來控制Pareto最優解層個數，消除局部收斂。

1.2 擁擠度改進

NSGA2算法采用擁擠距離dc，i來評價個體的分布，并根據個體的dc，i來決定個體的優劣，但沒有考慮每一非支配層上個體分布的均勻性，在一定情況下，會破壞個體分布的均勻性。

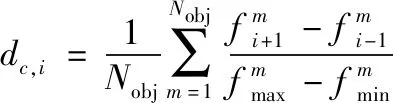
(2)

為了改善個體分布的均勻性，在擁擠距離計算的基礎上采用動態的擁擠度評價方法。

(3)

式(3)中，Vi表示相鄰的兩個體之間的差異。

1.3 交叉算子改進

NSGA2算法一般采用SBX交叉算子，其機理是模擬二進制交叉算子，對實數編碼的父個體進行交叉操作，即隨機得到交叉點位置，交換兩個父個體交叉點兩側的基因代碼。為了使算法具有更好的全局搜索能力，更好地保持種群的多樣性，采用算術交叉算子對NSGA2的交叉操作進行如下的改進。

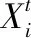
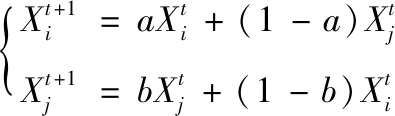
(4)

式(4)中，a、b為[0，1]上均勻分布的隨機數。

1.4 算法終止改進

NSGA2算法采用最大進化代數作為終止條件。最大進化代數設置的太小可能得不到優化效果，設置太大會增加許多不必要的計算量。為了解決此問題，提出一種改進終止判斷準則，在設置的最大進化代數下，如達到一定的條件即可終止計算，以保證獲得最優解的同時減少計算量，提高運算效率。

算法終止條件：在算法進行中，如果出現相鄰GAP代的種群距離小于設定閾值時，并能連續T(T表示能提高結果分布性參數)次保持這種穩定性，則計算終止，輸出結果。

相鄰GAP代的種群的距離計算方法為：如P，Q分別為兩個Pareto優解集，求出P中的每一個個體到對應Q中每一個個體的歐氏距離，以其中的最小值作為P中的該個體到Q的距離，求出P中的所有個體到Q的距離后，再求所有距離的平均值，即為相鄰GAP代的種群的距離。

閾值的設置方法為：如多目標優化有M個目標函數，首先根據初始種群確定各目標中絕對值總體相對較小的目標為fi，i∈[1，2，…，M]；然后再根據已得目標函數值確定|fi|的最大值為Δ，以Δ的某一比例值定為閾值。

2 優化模型的建立

葉輪是泵的主要關鍵部件，本研究主要是對燃油泵的葉輪進行優化設計。葉輪的設計包括很多參數，選擇對泵性能會產生綜合影響的關鍵幾何參數作為優化變量。主要包括葉輪的進口直徑D1，葉輪出口直徑D2，葉輪進口處寬度b1，葉輪出口處寬度b2，葉片進口安放角β1，葉片出口安放角β2和葉片數z，其他參數對泵性能影響較小，可使用既有的經驗值。優化變量集為：

X=[x1,x2,x3,x4,x5,x6,x7]T=

[D1,b1,β1,D2,b2,β2,z]T

優化設計的目的是使優化對象達到所需的性能指標。因此在優化設計中，正確地確定目標函數是非常關鍵的，目標函數的確定與優化結果和計算量有著密切關系。在確定目標函數時，應該注意到工程實際要求，并能客觀反映設計變量與優化目標的關系。同時為使優化結果更具真實性和可靠性，建立的優化目標數學模型應能客觀反映出優化對象的本質。航空燃油泵是一款航空產品，要求質量輕，效率高；對于泵，要避免出現空化和揚程駝峰，輸送液體性能滿足預定要求。因此建立燃油泵總損失、汽蝕余量和揚程-流量曲線斜率三個目標函數。

2.1 泵總損失目標函數

泵總損失主要包括機械損失、容積損失和水力損失三部分，泵內部功率總損失的表達式：

ΔP=Pm+Pv+Ph

(5)

其中：

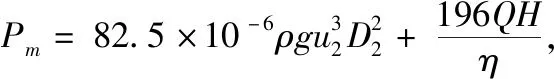
Pv=ρgqHt，容積損失(W)；

Ph=ρgQ(Ht-H)，水力損失(W)；

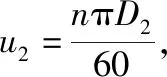
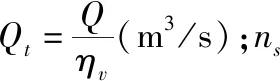
泵壓力損失值表達式為：

Δp=ΔP/Q

(6)

綜上，第一目標函數表達式為：

f1(x)=min(Δp)

(7)

2.2 汽蝕余量目標函數

(8)

式中，λ取值0.4～1.78，以提高泵的效率為首要目標，此處取大值。

第二目標函數表達式：

f2(x)=min[(NPSH)r]

(9)

2.3 揚程-流量曲線斜率目標函數

泵揚程-流量特性曲線的斜率為

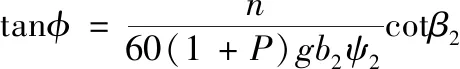
(10)

斜率數值越大，越不容易出現揚程駝峰。算法中目標函數統一以最小值計，可將此式改寫為倒數形式。

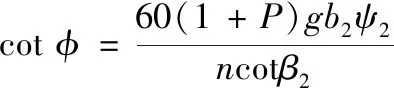
(11)

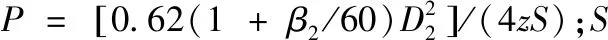
第三目標函數表達式：

f3(x)=min(cotφ)

(12)

3 優化實例

以某型離心式燃油泵為優化原型，其設計性能參數如表1所示。

表1 燃油離心泵性能參數

根據速度系數法[9]以及大量離心泵優化經驗，并結合原型泵的相關參數，給出本設計各優化變量的約束條件。

葉輪輪轂直徑dh直接影響葉輪流道幾何尺寸，葉輪輪轂直徑又由泵軸最小直徑d確定。根據泵的性能參數可以估算出泵功率，再根據選用的材料得到泵軸最小直徑。因航空產品要求質量盡量輕，減少能耗，所以泵軸選用剪切強度高的合金材料，計算取葉輪輪轂直徑為30 mm。

前述的各優化變量的取值范圍如下：

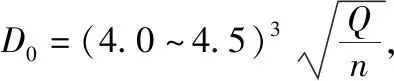
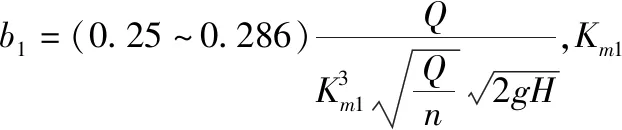
相關研究表明當葉片數和出口安放角滿足條件z0.773β2<90，可消除揚程駝峰。因此根據上述葉片數，可得到葉片出口安放角的取值范圍。

葉片進口安放角要根據液流角和沖角計算，本優化變量參照泵原有的進口安放角設置。

由上述，根據約束條件，得到優化變量的取值范圍如表2所示。

表2 優化變量取值范圍

采用Matlab的遺傳算法工具箱進行離心泵葉輪的優化設計計算[10-11]。種群規模N：100；最大進化代數MAXGEN：250；交叉概率Pc：0.85；變異概率Pm：0.01；算法終止條件的閾值：Δ的千分之一；相鄰兩個種群間隔代數GAP：5；提高結果分布性參數T：10。

使用改進NSGA2算法進行葉輪優化計算，優化結果的目標空間分布如圖2所示。

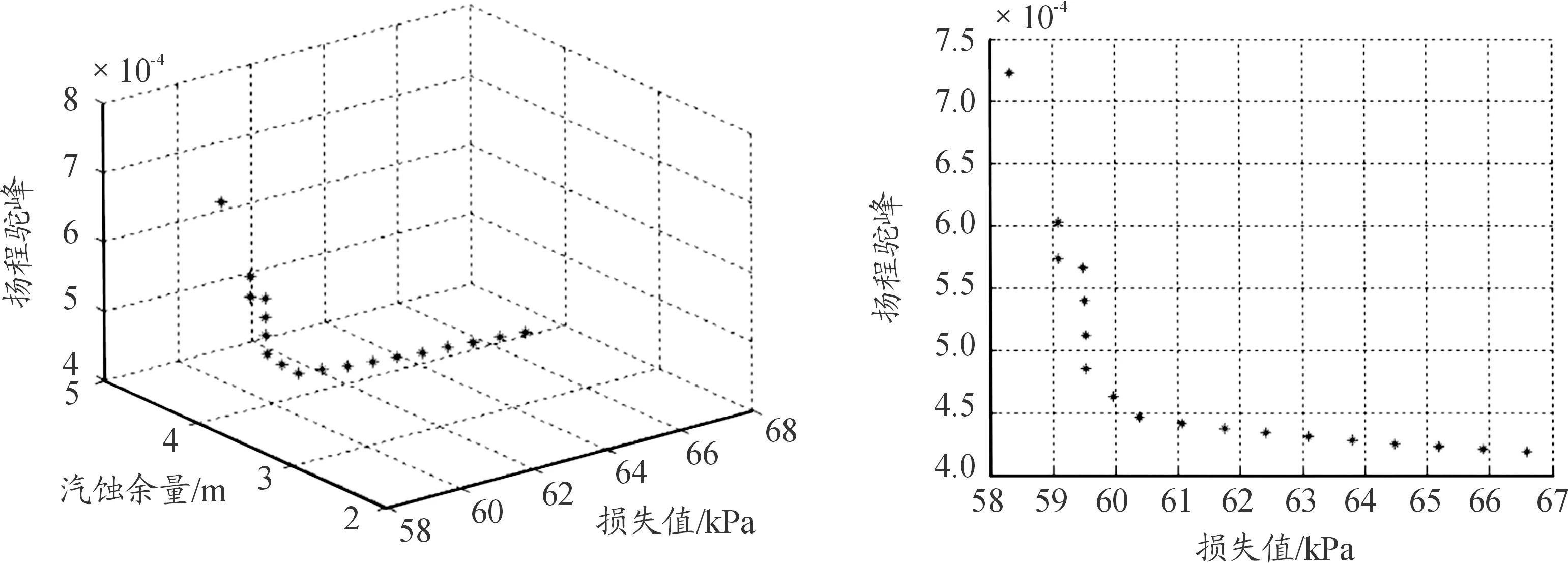
圖2 最優解分布(優化1)

為進一步驗證改進NSGA2算法在燃油泵優化設計中的優越性，將泵轉速也增加為優化變量(取值范圍5 000～6 000 r/min)，其他優化變量取值范圍不變，目標函數和算法參數都不變，優化結果的目標空間分布如圖3所示。

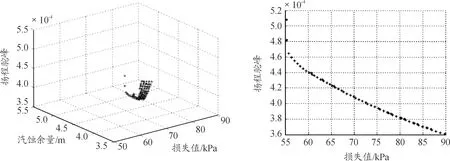
圖3 增加轉速優化解分布(優化2)

根據前述的優化目標，從兩次優化結果中分別選取優化解，選取的原則是泵損失值盡量小，不出現空化和揚程駝峰，還要能使泵總尺寸減小。最終選取的優化解如表3所示，其中優化1損失值61 kPa左右，優化2損失值70 kPa左右。與傳統設計的變量相比，可以看出優化后葉輪的出口直徑減小6 mm，蝸殼基圓也可相應減小，使泵的總尺寸也減小，重量減輕，契合航空產品設計要求。

表3 優化解

為驗證優化后泵的性能，根據表3中的優化變量，分別建立3種設計方案的三維模型(蝸殼泵)，利用流體仿真軟件(CFX)對3種方案泵的性能進行仿真分析[12]。

圖4為3種設計方案的壓力-流量性能曲線，從圖中可以看出，優化設計方案得到的性能曲線在設計工況點(Q=0.003 3 m3/s)的增壓值能滿足泵工作要求。與傳統方法相比，曲線變平坦，壓力變化較小，沒有出現揚程駝峰。

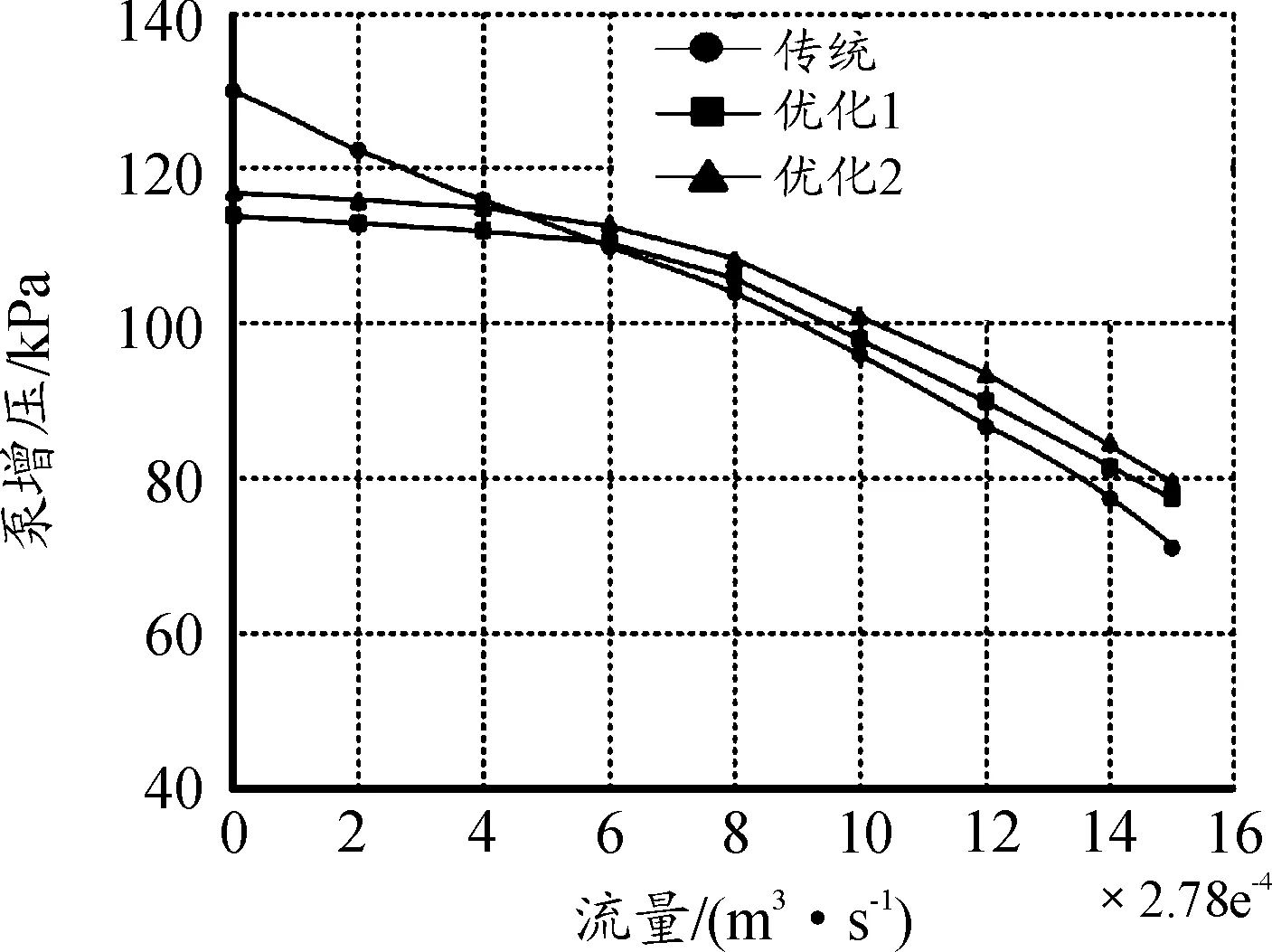
圖4 三種方案壓力-流量性能曲線

影響泵壓力-流量曲線的相關因數有葉輪出口直徑、出口寬度和出口安放角。優化后，D2減小導致兩次優化的關死點揚程減小，但優化2的轉速比優化1略高，因此關死點揚程也略大；b2、β2增大使揚程-流量曲線斜率變小，因此優化后曲線變平坦。這說明采用改進NSGA2算法的優化設計方案是可行的。

圖5為三種設計方案在各工況點的效率-流量曲線，從圖中可以看出，在設計的工況點，優化設計方案的效率比傳統設計方案的效率有所提高，最高可提升3.5%。

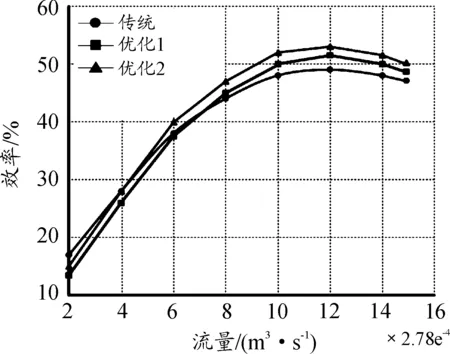
圖5 三種方案效率-流量對比曲線

影響泵效率的相關因數有葉輪出口有效過流面積、進口直徑和出口安放角，其中出口有效過流面積與D2和b2乘積相關。優化后，進口直徑和出口安放角變化不大，但葉輪出口有效過流面積明顯增加，這對提高泵效率有益。這說明采用改進NSGA2算法的優化設計對提高泵的效率是有幫助的。

由圖5可以看出，不管哪種方案，泵的最高效率僅在50%左右，這是因為流體仿真中燃油泵葉輪均采用的單圓弧直立形式葉片，這種形式葉片流道中將會出現漩渦與回流(如圖6)，影響泵的效率。如要再進一步提升效率，需要改用扭曲葉輪，因為高比轉速泵需要采用扭曲葉輪更合適。但扭曲葉輪制造困難成本高，從經濟角度考慮，如直立葉輪可滿足使用要求亦可采用。

圖6 流體仿真

采用改進NSGA2遺傳算法，在滿足泵的設計性能下可使泵的尺寸減小7.7%左右，泵的效率提升2.5%左右。進一步再將泵轉速也增加為優化變量，優化后泵尺寸與優化1基本不變，效率可再提升1%。

根據優化2結果制作樣機與傳統設計的原型泵相比，效率提升2%左右。

4 結論

以燃油泵的損失最小、氣蝕余量最小和消除駝峰曲線為設計目標，將改進NSGA2遺傳算法應用到航空燃油泵的優化設計中，在滿足泵的設計性能條件的情況下，可有效減少泵尺寸，提高泵效率。

改進NSGA2遺傳算法在泵的優化設計上有著傳統方法所無法比擬的優越性，一次性完成優化設計，避免反復設計試驗，有效縮短了設計周期，降低設計成本。

本研究為泵的設計提供了一種新方法，具有理論意義和工程應用價值。