基于LSTM-SVM的卷對卷系統預測性維護模型

黃冠澤

（廣東工業大學，廣州 510006）

0 引言

隨著柔性材料加工技術的快速發展，柔性薄膜材料的制備工藝也不斷得到完善。新型柔性薄膜材料制品，如柔性電路板、太陽能電池薄膜等在各個行業的使用日益增多。柔性材料卷對卷設備（Roll to Roll，R2R）作為薄膜材料的主要生產設備之一，被廣泛應用到柔性電路板（FPC）、有機發光二極管（OLED）、太陽能電池薄膜、干粘合劑等柔性薄膜材料的制備生產當中[1-3]。卷對卷設備加工過程具有高速、高精度、持續生產的特點。當其核心零部件發生性能衰退，加工精度將大幅度下降，引起柔性薄膜產品的變形，使得良品率降低，造成經濟損失。非常有必要對卷對卷設備進行預測性維護。

近年來，有學者進行了LSTM（Long Short-Term Memory）在預測性維護領域的應用研究[4-7]，取得了一定進展，證明了LSTM 網絡在預測性維護領域應用的可行性。但是LSTM網絡的預測結果仍存在誤差疊加及預測結果滯后[8]、學習速率低[9]等問題。Funa[10]中提到，建立RUL 預測模型時，傳統的LSTM模型不能合理利用在線數據和非生命周期數據。

金樑[11]中提出一種SVM 算法加權融合LSTM 算法的模型，在短期電力負荷預測實驗中得到不錯的結果，預測誤差小且速度快，表明SVM 對于LSTM 神經網絡具有降低預測滯后率的效果。因此，本文提出了LSTM-SVM 算法融合預測模型，將完整且經過訓練的LSTM 模型的softmax 輸出層更換為SVM分類器，再進行SVM分類器的訓練，最后得到LSTM-SVM算法融合模型。又由于自身算法的抗擬合特性，SVM 常被用于解決神經網絡過擬合的問題[7]，提升算法融合網絡的抗過擬合特性。SVM 在處理低維數據分類問題時，速度更快，精度更高，作為網絡的輸出層時，能很好地對LSTM網絡所提取的特征數據進行分類。最后經過實驗證明，本文提出的LSTM-SVM 算法融合預測模型得到的健康狀態層級多，預測精度高，能很好地進行卷對卷設備預測性維護。

1 LSTM-SVM神經網絡模型框架

本文提出了一種基于LSTM 神經網絡和SVM 神經網絡的性能衰退預測模型——LSTM-SVM模型。圖1所示為性能衰退預測模型的結構。該模型由兩部分組成，第一部分是深度遞歸循環神經網絡，采用LSTM神經網絡從原始輸入向量中提取數據特征；第二部分是用來進行特征分類的SVM神經網絡輸出層。LSTM神經網絡最后一層的隱含層表示作為設備健康狀態概括的表示輸入到SVM神經網絡層中。

該融合模型的訓練方式為：首先訓練LSTM模型，將軸承振動加速度數據經過標準化后輸入到網絡中，然后獲得經過調整的神經元參數，輸出隱含層信息。將隱含層信息輸入到SVM分類器中，進行特征數據的分類，從而獲得健康狀態。

圖1 LSTM-SVM性能衰退預測模型

2 基于LSTM-SVM 的卷對卷設備性能衰退預測模型建模

2.1 LSTM（Long Short-Term Memory）

LSTM 是RNN（Recurrent Neural Network）的改進模型之一，即LSTM 也是遞歸神經網絡，具有遞歸神經網絡的特性，常常被用于處理時間序列數據。當LSTM處理分類問題時，其輸出層一般為softmax 邏輯回歸網絡[12]。該模型的基本單元是記憶模塊，包含記憶單元和3個控制記憶單元狀態的門結構，分別是遺忘門、輸入門和輸出門。遺忘門決定從記憶狀態信息中遺忘相關度低的歷史信息，而輸入門決定記憶單元狀態對輸入數據對的敏感程度，輸出門決定輸出該時刻的信息。圖2 所示為t時刻的LSTM 記憶模塊狀態。ft、it、ot分別為t時刻遺忘門的狀態值、輸入門的輸入和輸出門的輸出；ht-1為記憶模塊輸入的隱含信息；ht為記憶模塊輸出的隱含信息；xt為t時刻的輸入向量；gt和kt為計算過程為了方便計算而設定的中間量；Ct-1為t-1時刻的記憶單元狀態；Ct為t時刻的記憶單元狀態；C~t為記憶單元的中間狀態。

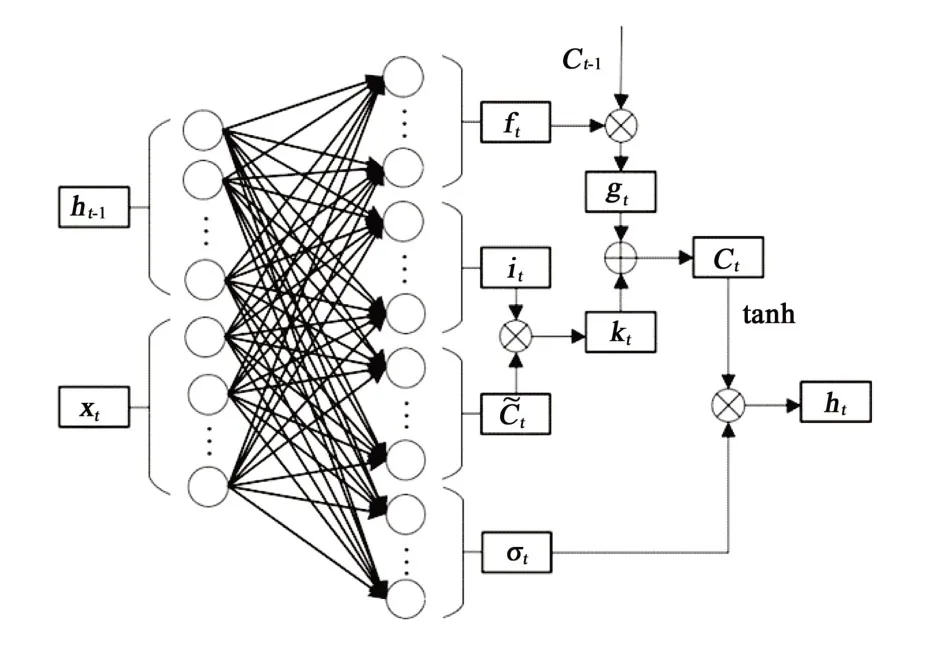
圖2 LSTM記憶模塊

LSTM記憶單元狀態更新和輸出信息的過程如下。首先，通過遺忘門刪除相關度低的歷史信息：

然后，輸入門根據輸入信息和歷史信息來更新序列信息：

設gt=ft×Ct-1，kt=it×C~t，則有Ct=gt+kt。最后，輸出t時刻的信息為：

式中：U為隱含狀態h的權重矩陣；W為輸入狀態x的權重矩陣；Uf、Ui、UC、UO、Wf、Wi、WC、Wo分別為對應門的權重矩陣；bf、bi、bC、bO分別為對應門的偏置向量；σ為sigmoid激活函數；tanh為雙曲正切激活函數。

LSTM 網絡需要設置的超參數Input time step、Input Dimension、Output Units、Batch Size、Epoch、Optimizer、Learning Rate、Decay、Dropout rate 等。Input time step 為時間步，即每次輸入數據的長度；Input Dimension為輸入維度，即輸入數據的維度；Output Units 為輸出類，即輸出層輸出類別的數目；Batch Size 為單次訓練樣本數；Epoch 為模型訓練次數；Optimizer為優化算法，即將模型梯度下降的算法；Learning Rate為模型的學習率，可直觀表示模型的學習性能；Decay為衰減率，是正則項的一個系數，控制權值衰減的速率，用于防止過擬合；Dropout rate 為丟失率，用于在模型訓練途中，去掉冗余的神經元，留下貢獻更高的神經元，以提高模型性能。

2.2 支持向量機

支持向量機（support vector machines, SVM）是一種用于解決二分類問題的模型，通過求解數據簇在特征空間上的最大間隔來進行線性分類。添加核函數后，SVM 轉變為非線性分類器。間隔最大化是SVM的學習策略，具體為求解凸二次規劃。其基本過程是求解劃分訓練數據簇并且幾何間隔最大的超平面，用w·x+b=0 表示。在平面上，w 可視為直線的斜率，b為直線的截距。

對于給定的數據集T={(x1,y1),(x2,y2),…,(xN,yN)}和分離超平面w·x+b=0，超平面關于樣本點的幾何間隔定義如下式所示：

具體地，K(x,z)是一個函數，或正定核，存在一個映射φ(x)，對任意輸入空間中的x，z，都滿足下式條件：

K(x,z)=φ(x)·φ(z) （8）

用核函數K( x, z )代替內積，求解得到非線性支持向量機。參數α*為拉格朗日乘子，且α*>0。

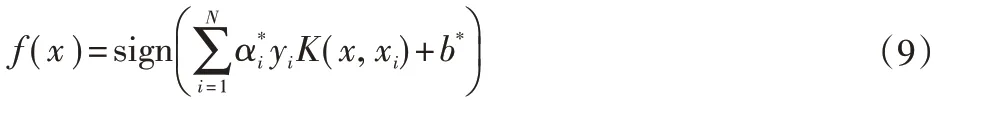
非線性支持向量機的學習算法如下。

輸入：訓練數據集T={( x1, y1), ( x2, y2), …, ( xN, yN)}。其中，xi∈?n，yi∈{+1,-1}，i=1,2,…N。

輸出：分離超平面和分類決策函數。選取適當的核函數K(x,z)和懲罰參數C>0，構造并求解凸二次規劃問題。其中，0 ≤αi≤C，i=1,2,…N。

選擇α*的一個分量滿足條件

得到最優解分類決策函數如下式所示：

高斯核函數是SVM處理非線性問題的常用核函數，如下式所示：

將上式代入分類決策函數，得到下式：

根據以上理論不難看出，SVM 算法在處理低維數據分類問題時，由于其算法復雜程度低，可以同時進行大量數據的計算，計算效率極高，且精度較高。結合SVM自身的抗擬合特性，其常被用于解決神經網絡過擬合的問題，提升了算法融合網絡的抗過擬合特性。作為網絡的輸出層時，能很好地對LSTM網絡所提取的特征數據進行分類。

構建SVM分類器，需要設置懲罰參數C和幾何間隔γ，C用來約束α*i的范圍，防止模型出現過擬合和欠擬合的現象。為了簡化計算，可將γ設置為1。

2.3 LSTM-SVM神經網絡模型參數

根據上述原理，構建LSTM-SVM 神經網絡模型，表1 所示為LSTM網絡的參數設置情況。時間步與輸入數據的長度相同，設置為1000。由于數據的維度對本實驗的影響不大，不對數據進行壓縮，故輸入維度為1維。輸出類與數據標記類相同，即為健康狀態的個數，定為100類。由于訓練模型的計算機顯卡并行計算的特性，單次訓練樣本數需要定為2 的冪次方，即2、4、8、16、32、64 等。根據實驗數據量，取32 為單次訓練樣本數，有助于模型的訓練。將模型訓練次數設置為15 次，觀察模型損失值的變化。RMSProp 優化算法是AdaGrad算法的一種改進，加了一個衰減系數來控制歷史信息的獲取多少，所以在優化用于處理時序問題的模型時，更具有優勢。學習率根據經驗默認為0.001；衰減率定為0.9，防止因樣本數量小而導致過擬合；丟失率定為0.5，即在每次訓練過程中，將模型中一半的神經元清零，以提高貢獻度高的神經元的權重。

表1 LSTM網絡參數設置

表2 所示為SVM 層的參數設置情況。懲罰參數C用來約束的范圍，防止模型出現過擬合和欠擬合的現象，取中值，設為0.5。在低維問題中，幾何間隔的值對SVM分類器的性能影響不大，為了簡化計算，可將γ設置為1。以此，訓練SVM分類器100 個，作為LSTM-SVM 的輸出層，劃分卷對卷設備的健康狀態。

表2 SVM層參數設置

3 LSTM-SVM性能衰退預測模型試驗研究

3.1 搭建實驗平臺

圖3 為搭建LSTM-SVM 性能衰退預測模型實驗平臺，用于驗證LSTM-SVM 性能衰退預測模型的性能。該平臺為安捷利FPC 產線的收卷裝置，是FPC 產線制備柔性電路板的關鍵裝備之一。在其輥軸上安裝振動加速度傳感器，將傳感器連接采集卡以采集數據。在完整的壽命周期中，采集軸承的振動信號。實驗條件參數如表3所示。數據的采集頻率為20 kHz，每10 min采集1次，每次采集20480個數據點。

圖3 LSTM-SVM 性能衰退預測模型實驗平臺

表3 實驗條件參數

為了訓練網絡模型，需要在計算機上搭建虛擬環境，其配置如表4所示。采用了Pycharm作為網絡模型程序運行的編譯器，并在其環境中調用常見的AI 模型框架Tensorflow 作為LSTM-SVM模型的框架。

表4 虛擬環境搭建配置

3.2 實驗測試及結果分析

LSTM-SVM 性能衰退預測模型針對卷對卷設備輥軸出現的性能衰退問題，對其進行性能衰退預測，為設備維護提供決策依據。卷對卷設備高速運行，重要組成部分即將失效，將導致設備整體報廢，造成嚴重損失。現在對其進行性能衰退預測實驗。

實驗分為兩部分。首先，使用訓練集訓練神經網絡模型。然后，使用驗證集驗證已訓練模型的性能。對數據情況進行分析。

R2R 設備性能衰退有4 個狀態，分別為性能良好狀態、前期衰退狀態、中期衰退、輥軸失效等。可以用相應的原始軸承信號表示，在不同性能狀況下軸承振動信號如圖4所示。

從良好狀態的振動信號數據中隨機取10組數據，標記為最高健康狀態（即滿分100，分值為0～100，0 為衰退失效），再從前期衰退狀態到輥軸失效狀態間的振動信號數據中，按比例取100 組數據作為訓練集，依次標記為99、98、97、…、1、0分。同理，另取110 組數據作為驗證集。每組數據含數據點1000 個，采樣時間為0.05 s。對應網絡模型結構為1000-100-100-100，即輸入層含1000 個神經元，輸出層含100個SVM分類器，即輸出100類。另外，兩個隱含層的含100個神經元。

圖4 原始軸承振動信號

為了評估LSTM-SVM 模型在性能衰退預測上的性能，采用損失值和準確度來量化LSTM-SVM 模型的性能。損失值是預測值和真實值之間概率分布差異的量化，損失值越小則表明預測值越接近真實值，損失值的計算公式下式所示。

式中：y為真實值；y^為預測值；w為模型參數。

準確度為模型輸出結果的總結，能直觀表現模型的預測性能。準確度越高表明模型性能越好。

訓練模型得到其損失函數曲線如圖5 所示。可以看出，當LSTM-SVM 模型訓練第7 次時，訓練集的損失值基本收斂到0.47，繼續訓練模型得到的收益較低。而驗證集在模型訓練第8次時，這是由訓練集和驗證集的數據差異性導致的，所以驗證集的損失值收斂在0.38，優于訓練集的結果。

圖5 LSTM-SVM模型的損失函數曲線

圖6 LSTM-SVM模型的預測準確度曲線

模型訓練過程中準確度曲線如圖6 所示。實驗結果最終得到，訓練集的準確度為0.620，驗證集的準確度為0.535。因為模型采用訓練集來訓練，對訓練集的擬合程度更高，故準確度比驗證集高。

表5 模型訓練效果對比

為了驗證LSTM-SVM模型的預測性能，本研究建立了LSTM-SVM模型與LSTM 模型的對比實驗。LSTM 模型使用相同的訓練集和驗證集。經過驗證，兩種模型的效果對比如表5所示。

通過兩種預測模型的對比實驗，可以發現LSTM-SVM 的訓練速度比LSTM模型快很多，而且精度也有所提升。

4 結束語

本文針對柔性材料卷對卷設備的性能衰退問題，提出了一種LSTM-SVM 性能衰退模型。通過實驗發現LSTM-SVM 模型有效預測了卷對卷設備的性能衰退情況，成功劃分了設備的健康狀態且模型擬合情況良好，表明該模型在卷對卷設備性能衰退預測方面具有可行性。最后進行了對比實驗，發現LSTM-SVM的訓練速度比LSTM模型快很多，而且預測精度也有所提升。該結果表明SVM 能很好地對LSTM 網絡所提取的特征數據進行分類。這是因為模型很好地融合了SVM在處理低維數據分類問題時的優越性。而更快的學習速率意味著，當算力一定時，用于訓練的數據規模可以更大，這對于工業大數據而言十分具有應用前景。綜上，本文提出的LSTM-SVM 性能衰退預測模型得到的健康狀態層級多、訓練時間短、預測精度高，能很好地進行卷對卷設備預測性維護，為后續的柔性材料卷對卷加工決策系統提供重要決策依據。