球形輪組結構及其控制系統設計*

翟建麗，莫浩明，曾德勝，周 杰，王可涵，陸厚霖，胡恰鋒，王作桓

（廣東工業大學華立學院，廣州 511300）

0 引言

輪式移動作為運輸工具的主要形式，其制造簡便和價值成本低，而球形輪組具有靈活性、占地面積小、易于搬動，可以運用在代步工具、機器人和危險地帶運輸等。國內外為此做了大量研究，球形輪組結構最早應用在機器人中。2006年美國卡內基梅隆大學將球形輪組結構運用在BBR機器人[1]；2008年日本東北學（TGU）采用3 個全向輪結構驅動技術和2010年蘇黎世理工聯邦理工學院開發了類似于TGU 的原型，具有較高的魯棒性[2]；2019年加州大學圣地亞哥大學對BBR機器人的機械設計、動態分析等[3]；2012年同濟大學的單球機器人建模和控制[4]；2014年以阮曉鋼為首對獨輪機器人進行自抗擾研究[5]。

本文根據球形輪組的工作原理和自身存在的非線性、強耦合和欠驅動等問題進行研究。利用三維建模軟件建立物理模型進行動力學分析，設計控制算法與ROS 系統建立的上位機聯合，利用注模技術建立樣機對球形輪組進行研究。

1 球形輪組設計

1.1 機械結構設計

球形輪組由3 個全向輪、球輪和車身組成，車身上搭載電源、監測系統、控制系統和執行系統等部分構成，如圖1所示。全向輪通過聯軸器直接與電機連接，控制電機的力矩間接控制全向輪在球輪上的轉速和方向，機身由兩層構成，在頂層用于固定電源和主控板，主控板包括控制模塊和監測模塊；底層用于固定與全向輪直接連接的電機。

圖1 物理模型設計圖

當全向輪組受到外界干擾時，3個全向輪通過驅動球輪朝傾斜方向運動來維持自身平衡，俯視圖下與電機相連的3個全向輪兩兩相互成120°，因此通過控制電機的力矩調整全向輪的轉速和方向，俯視圖下全向輪分布簡圖如圖2所示。

圖中，vr1,vr2,vr3分別為3個全向輪的速度，v為某一時刻的速度，根據公式推導出3個全向輪的速度和某一時刻的速度關系式如下所示：

式中：vr1～vr3為全向輪1～3的速度；v為某一時刻的速度。

球形輪組通過利用MPU6050陀螺儀傳感器監視機身的姿態變化，并進行處理后傳入給控制模塊，及時做出反應去調整電機的轉速和方向。球形輪組在平面上的運動速度與全向輪速度的關系，在xy平面內的運動簡圖如圖3所示。

圖2 全向輪分布簡圖

圖3 運動簡圖

根據簡圖和公式推導出如下的速度關系式：

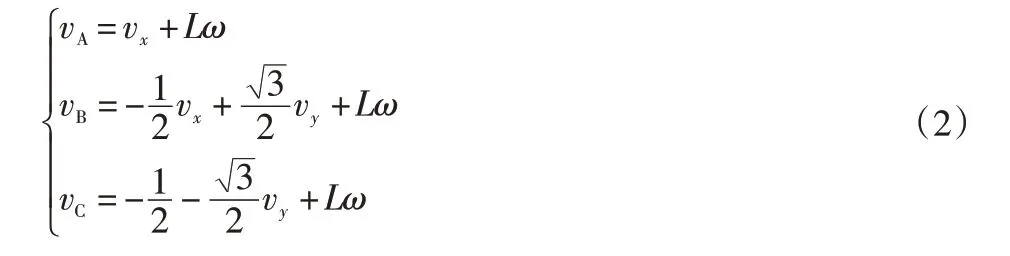
式中：ω為輪組的角速度；L為全向輪的中心與底盤的中心距離；vA、vB、vC為3個全向輪的轉速；vx、vy為球形輪組在x、y方向的運動速度。

1.2 電氣設計

球形輪組為了保證自身姿態平衡的同時，保證在平面內任意方向移動，其電氣部分需要包括電源、監測、控制和執行部分——電機。電源是為各設備提供穩定的電壓，另外需要考慮到整體的重量和體積，因此需要選擇重量輕和體積小的電源。因此采用12 V的鋰電池作為總電源，分別通過電機驅動和電壓轉換器提供相應電壓給電機、控制系統和MPU6050陀螺儀傳感器等。

監測系統采用陀螺儀傳感器可以實時監測球形輪組的姿態變化和速度變化；控制系統中采用STM32 芯片，可以根據監測系統采集的數據進行計算處理獲得直流電機的控制變量；執行系統根據控制部分的控制變量去控制電機的扭矩。

根據球形輪組的機械結構與電氣部分的設計，利用注模技術建立試樣機的機身，根據圖1 的設計圖設計的試樣機如圖4所示。

圖4 實物圖

圖5 物理模型簡圖

2 動力學分析

球形輪組是一個多剛體機械結構，非線性、強耦合和欠驅動，為適應自身的自平衡，需要設計一套控制算法。在設計控制算法前需要先進行動力學分析，因為與外部環境接觸受到干擾，需要根據控制部分的控制變量來控制電機的力矩，所以需要考慮球形輪組的電機驅動扭矩與驅動輪的力和力矩。球形輪組屬于多剛體結構，因此采用拉格朗日方程對球形輪組的動力學分析，可以不考慮剛體內部的關系，同時把球形輪組分成全向輪、球輪和機身三部分。如圖5 的物理模型簡圖所示，由于球形輪組是一個質心高于支點的特征，在自身重力作用下無法保證球形輪組的自身平衡。根據全向輪與球輪和電機的電機關系，有利于非線性控制算法的設計，其拉格朗日方程[6]為：

式中：T為系統總動能，W為系統總勢能。則：

通過拉格朗日方程建模和分析，得到電機在球輪上的力矩為：

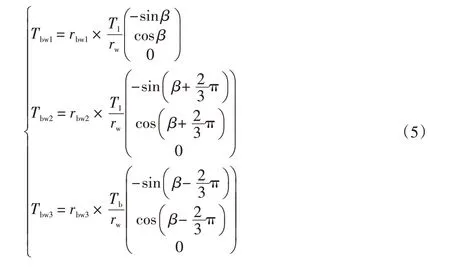
3個電機的實際力矩為：

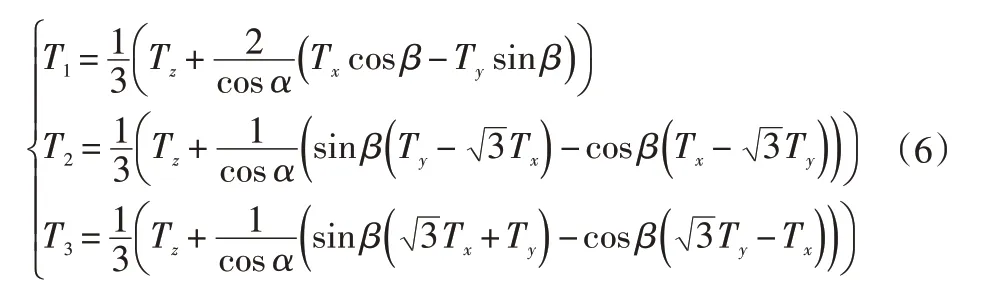
式（3）～（6）中：T為總動能；W為總勢能；下標b、w、a分別為球輪、全向輪、機身；Tb為電機在球輪上的力矩；rw為全向輪半徑；T1、T2、T3分別為3個電機的實際力矩。

依據剛體力學分析，部分零件不受到力的影響或者可以在球輪組內實現力系平衡，可以不考慮到整體運動中去，所以機械結構簡化后得到如圖5所示的物理結構簡圖。

3 控制系統

3.1 控制算法

球形輪組的控制主要包括自平衡控制與位置控制，采用兩個相同的LQR狀態反饋控制器分別對單球自平衡移動機器人等效的兩個一級倒立擺進行自平衡控制與位置跟蹤控制[7-8]。

理想情況如下：

（1）全向輪不與球面打滑，同時球面有足夠摩擦力；

（2）電機軸線中心正是底盤重心；

（3）各輪之間是絕對的互成120°安裝；

（4）電機軸線中心正是底盤重心。

軟件控制流程如圖6 所示，小車上電后，系統模塊進入初始化，系統進入當前狀態平衡點采集，采集完后進入系統5 ms 中斷服務函數，進行姿態數據采集和逆運動學計算，從而控制直流電機讓球形輪組處于動態平衡，系統不斷地進行5 ms 中斷從而進行小車姿態識別。其中姿態采集需要用到濾波算法才可得到穩定的姿態數據。濾波部分分別通過低通和均值濾波處理加速度計和陀螺儀的原始數據，然后通過互補濾波實現兩個數據的融合，從而獲得俯仰角和側傾角數據。

部分控制算法如圖7所示。

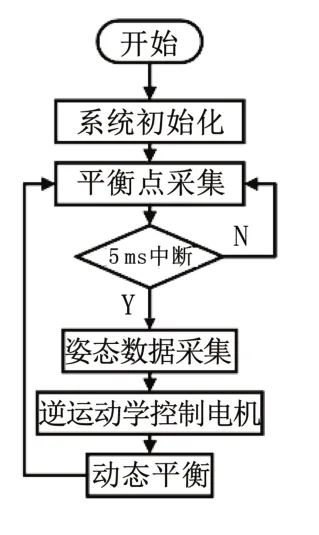
圖6 控制算法流程圖

圖7 部分核心代碼

3.2 控制系統

球形輪組的控制系統用來接收MPU6050陀螺儀傳感器獲取的姿態信息以及上位機發送的控制信息，最后根據所編寫的控制算法求出在某一時刻的狀態所對應的電機控制量。球形輪組的研究采用ARM公司的STM32F103ZET6芯片，其最高工作頻率為72 MHz，FLASH 為512 k 和32 位的CPU，具有豐富的I/O接口、庫函數和開源代碼，因此開發容易，并滿足球形輪組底層平衡控制的要求。

根據圖8 的硬件框圖所示，MPU6050 陀螺儀傳感器采集輪組姿態數據并經過卡爾曼濾波處理后輸入到控制系統ROS，然后與姿態平衡點的條件進行比較，MCU 根據姿態偏離程度向電機驅動發出糾正信號，驅動步進電機進行動態平衡調節。

圖8 硬件框圖

如圖9 所示，在MCU 上搭載好ROS 系統，在ROS 中輸入ifconfig命令查詢小車的IP地址，確保上位機控制端與小車是處于同一局域網下。接著修改控制端的bashrc 配置文件，把小車IP地址填入。因為小車是作為ROS的主節點，所以需要修改export ROS_MASTER_URI的地址為小車IP地址。完成上述步驟后，通過SSH 連接ROS 小車。可以用命令rosrun rviz rviz查看小車的rviz運動方向。用上位機控制小車運動和實時PID調參，如圖10所示。

圖9 rviz運動狀態查看

圖10 控制系統界面

4 仿真結構

結合上述對球形輪組軟、硬件的設計和分析，需要驗證其自平衡和控制系統的可實驗性。首先將建立的物理模型導入仿真軟件MATLAB 中，并結合串級PID控制的對應參數設置進行仿真性試驗，得出如圖11 所示的仿真對比實驗結果。由圖可知，球形輪組的姿態角與平衡值發生偏離時，控制模塊能夠及時接收到傳感器傳送過來的姿態數據與串級PID 控制算法結合計算出電機的控制變量，迅速改變電機的扭矩來調整相應全向輪轉動速度和方向，保證自身的平衡，但是不能保證與理想條件的平衡點相重合，因為研究過程中屬于一個理想條件下，沒有考慮到能量方面的損失。

圖11 仿真實驗

5 結束語

針對輪式移動運輸工具的不靈活性、占地面積大、不易于搬動的問題，本文提出了球形輪組結構和控制系統的設計，實現球形輪組無轉彎半徑并且靈活地運動。采用拉格朗日方程進行動力學分析，設計出結構最佳的球形輪組，推出電機扭矩與3個全向輪在球輪上的運動關系，據此設計出擁有傾角環、速度環、轉向環的串級PID算法，同時設定好PID參數的初始值。本文提出運用ROS 系統建立上位機實現人機交互，讓用戶時時刻刻能監控輪組的姿態并做出調整，同時進一步完善PID參數設置。仿真試驗驗證了串級PID對球形輪組自平衡控制的可行性。

最后針對球形輪組自平衡的實驗與實地測試，證明了拉格朗日力學分析的方法能更直觀地分析球形輪組物理結構與剛體力系劃分；ROS上位機在調試PID的方面具有快速反應、實時監控、簡化調試的優點。兩種方法互補，把抽象的物理力學平衡用程序實現，為此類復雜繁瑣的調試做出了系統的實施方案。