基于GIOWA算子的社會消費品零售額組合預測

余 凡，吳禮斌

（安徽財經大學，安徽 蚌埠 233000）

0 引言

社會消費品零售總額能夠反映出一個國家或者地區人們的物質文化生活水平，同時也是衡量社會商品購買力和零售業規模大小的重要參考指標。2019年的統計數據顯示，我國居民收入增速超過經濟增速，城鄉居民收入差在繼續減少，這些表現也直觀地反映在了居民消費數據上，近些年增長的消費數據可以從一定程度上說明政府相關政策實施的效果。但是2020年的社會消費狀況受到“新冠肺炎”疫情的影響，數據顯示，2020年上半年我國的社會消費品零售額較上年同比增長了-1.8%。消費、投資和出口是拉動經濟進步的三大驅動力，消費的不足必然影響經濟增長。

關于組合預測的研究，最早在20 世紀中葉，Schmitt就利用組合預測方法對人口進行預測，1969年，J.M.Bates 和C.W.J.Granger 進一步對組合預測的模型和其應用進行了深入的探究［1］，進入21世紀以后，又有學者把算子理論和決策理論進行結合，引入誘導有序加權平均（IOWA）算子和廣義誘導有序加權平均（GIOWA）算子，以預測精度作為誘導值，對基于IOWA 算子的組合預測模型以及基于GIOWA 算子的組合預測模型等進行了研究。陳華友（2005）引進IOWA 算子的概念，建立誘導有序加權平均組合預測模型，用數學規劃方法給出了組合預測模型的IOWA 權系數，并通過預測企業所得稅證明該方法能有效提高組合預測精度［2］。到目前為止已經有大量學者將組合預測模型應用到宏觀和微觀經濟等各個方面。劉青、楊桂元（2013）建立誘導有序加權調和平均（IOWHA）算子組合預測模型預測出安徽省2012-2015 年城鎮化水平［3］，與現有的安徽省2012-2015 年實際城鎮化水平相比，預測精度達到0.99以上，說明該組合預測模型預測效果非常好。鐘梅、楊桂元、袁宏俊（2015）在ARIMA、Logistic模型和多元線性回歸模型的基礎上，引入GIOWA 算子建立組合預測模型對2015-2017 年我國FDI 進行預測［4］，與現有的2015-2017年我國FDI 的數據相比較，預測精度在0.96以上。

而關于社會消費品零售總額的預測研究，國內學者主要利用ARIMA 模型、GM（1，N）等模型對其進行單項預測，例如張華初、林洪（2006）通過對1978-2005 年中國社會消費品月度零售總額的分析，建立了ARIMA模型，預測我國2006年和2007年的社會消費品零售額數據，提出應提高農村消費水平［5］。本文在多元線性回歸模型、Holt-Winters非季節指數平滑和多項式擬合三種單項預測模型的基礎上引入廣義誘導因子，利用變權重的組合預測方法，給出預測精度更高的社會消費品零售額預測。

1 社會消費品零售額單項預測

1.1 多元線性回歸預測模型

1.1.1 數據的來源及選取

分析影響社會消費品零售額的因素，選取與社會消費品零售額關系密切的影響因素：固定資產投資和全國居民人均可支配收入。本文選取1989-2019年的數據為研究對象，分別以1989年為基期的商品零售價格指數、固定資產投資價格指數以及消費價格指數對社會消費品零售總額、固定資產投資額以及全國居民人均可支配收入消除價格因素，研究消除價格因素后的實際社會消費品零售總額。其中，由于數據缺失，1989-2012 年全國居民人均可支配收入由城鎮居民人均可支配收入和與農村居民人均純收入按照城鎮與農村人口比重計算得出，本文所使用的數據均來自國家統計局網站。

1.1.2 多元線性回歸模型建立

將去除價格因素后的固定資產投資額（FAI）、全國居民人均可支配收入（PDI）作為自變量，將我國社會消費品零售額（TRSC）作為因變量，建立多元線性回歸模型。建模結果顯示其可決系數R2=0.9956，說明模型具有很高的擬合優度，且自變量固定資產投資額（FAI）和全國居民人均可支配收入（PDI）都能通過t檢驗，但是通過對模型進行拉格朗日乘數（LM）檢驗，模型存在一階序列相關，用廣義差分法對模型進行了序列相關性的修正，最終得到的預測模型如下：

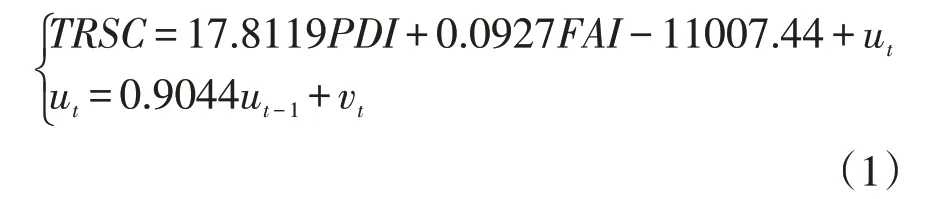
其中，ut為回歸方程的誤差項。

此時，R2=0.9989，，DW=2.03，模型擬合較好，可用于預測。預測結果見表4，記xt為各期的真實值，為預測值，用αt作為預測精度，表達式如下：

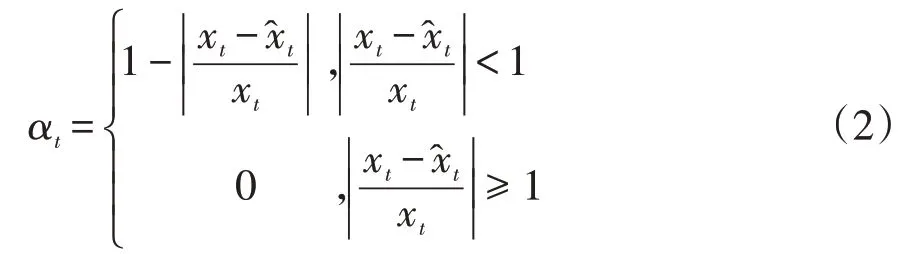
由多元線性回歸預測方法預測的樣本期（1990-2019 年）社會消費品零售額數據的精度較高，平均精度為0.9741，可用于后5 年數據的預測。因此，再分別預測出自變量，將2020-2024年的自變量的預測數據帶入（1）式的線性回歸方程，最終可得到2020-2024年的我國消除價格因素后實際社會消費品零售額的預測值。所以，利用多元線性回歸模型預測到我國2020-2024年的實際社會消費品零售總額分別為：184324.9 億元、190989.3 億元、197665.2億元、204350.9億元和211045億元。

1.2 Holt-Winters非季節指數平滑預測模型

不考慮其他影響因素，只考慮社會消費品零售額自身，可運用Holt-Winters 非季節指數平滑方法進行預測。考慮到數據的平穩性，將我國1989-2019年的社會消費品總額取對數，將對數化處理后的社會消費品零售額數據導入Eviews軟件，得到各項結果如表1所示。

表1 Holt-Winters指數平滑結果

由Holt-Winters 非季節指數平滑結果可知，趨勢項為0.06，觀測值截距為12.0867。由表4的預測結果可以看出，Holt-Winters 非季節指數平滑預測模型預測效果很好，在1989-2019 年的預測數據中平均精度達到0.9779。從而Holt-Winters 非季節指數平滑方法的預測公式為:

其中，t為時間，k為向后預測期數。當t=2019,k=1 時，則可得出2020 年社會消費品零售額的預測值。

所以，可由Holt-Winters 非季節指數平滑預測模型預測后5 年的社會消費品零售額，預測結果如表2所示。

表2 2020-2024年社會消費品零售額預測結果（億元）

1.3 多項式擬合預測模型

選取時間為影響因素，社會消費品零售額為因變量，建立關于時間的多項式擬合模型，通過建模分析，建立四次多項式的擬合優度最高，且預測精度很高，通過多項式擬合模型預測的我國社會消費品零售總額歷年的數據可以看出其預測精度很好，在1990-2019 年的預測數據中平均精度為0.9581，最終得到的預測模型為：

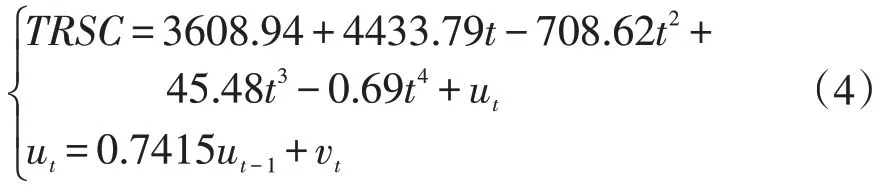
此時，R2=0.9991，=0.9989 ，模型擬合較好，因此，可以建立多項式擬合預測模型對我國2020-2024 年的社會消費品零售額進行預測，表3為利用多項式擬合模型得到的2020-2024年社會消費品零售額的單項預測結果。

表3 2020-2024年社會消費品零售額預測結果（億元）

表4是由三種單項模型得到的1989-2019年我國社會消費品零售總額的預測值，預測結果顯示多元線性回歸方程模型的平均預測精度最高，Holt-Winters指數平滑方法的預測精度次之，四次多項式擬合的預測精度最低。

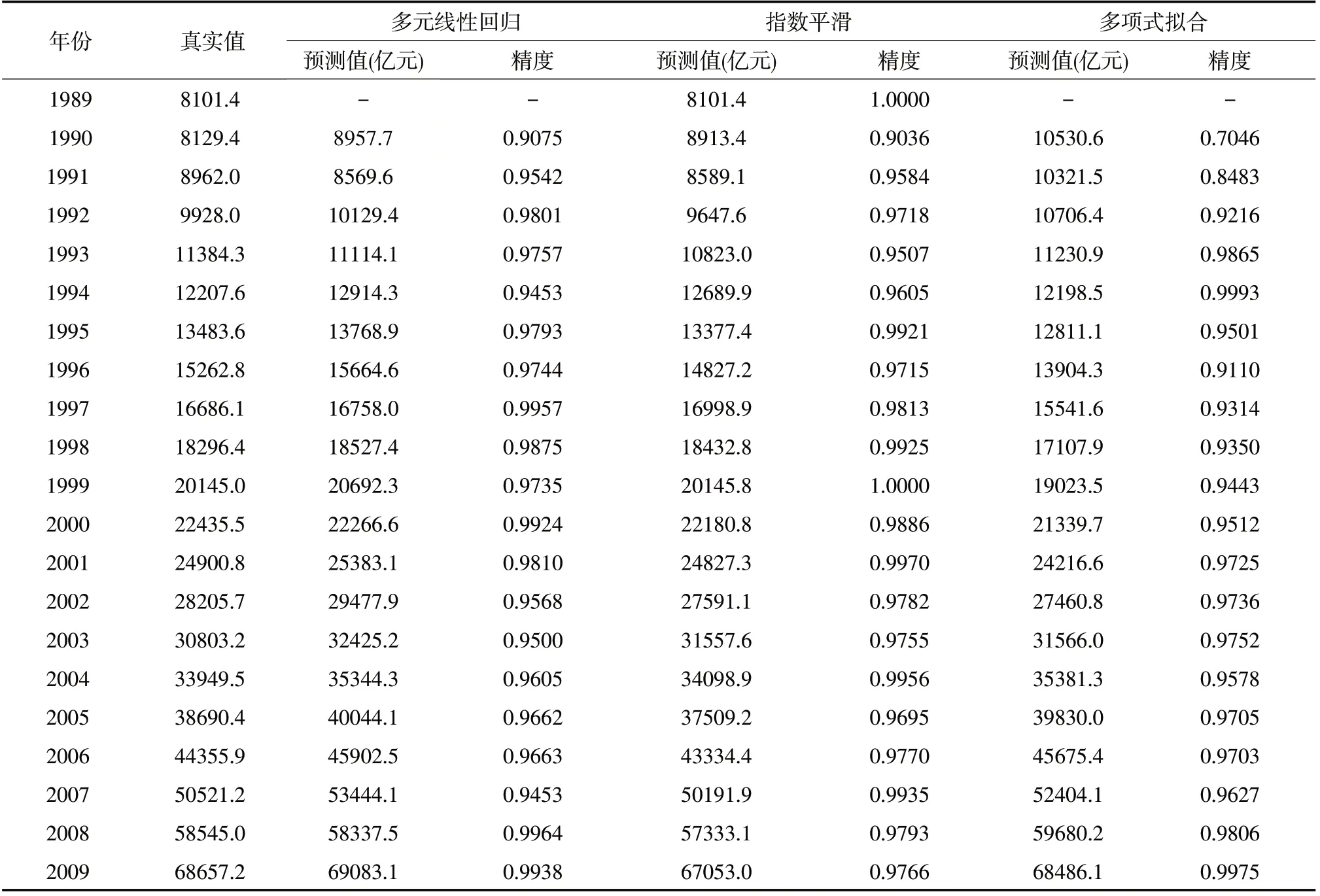
表4 三種單項預測結果

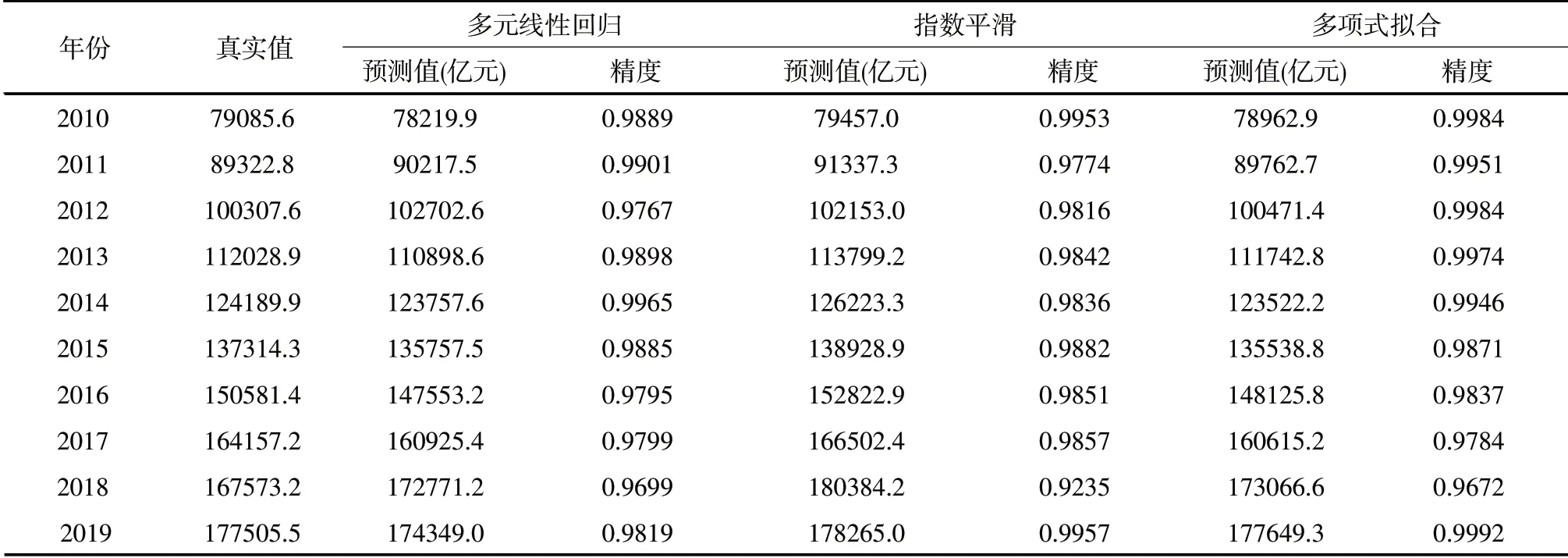
表4 三種單項預測結果（續表）

2 社會消費品零售額組合預測

為進行更高精度的預測，以預測精度作為誘導值，建立基于不同參數值的GIOWA 算子的組合預測模型，依次將樣本期（1990-2019 年）各個年份下的三種單項預測模型的預測值按照預測精度由大到小的順序重新排列，可得預測精度最高、預測精度次高和預測精度最差的誘導預測值和預測精度。

2.1 GIOWA組合預測模型相關概念

根據m種單項預測模型，建立廣義誘導有序加權平均（GIOWA）組合預測模型：

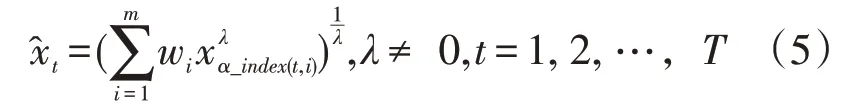
其中w1≥0,w2≥0,…,wm≥0,w1+w2+…+wm=1，α_index(t,i)是第t期中按精度從大到小順序排列的第i個大的數所對應預測值的下標，xa_index(t,i)是誘導有序第i種預測模型第t期的預測值。

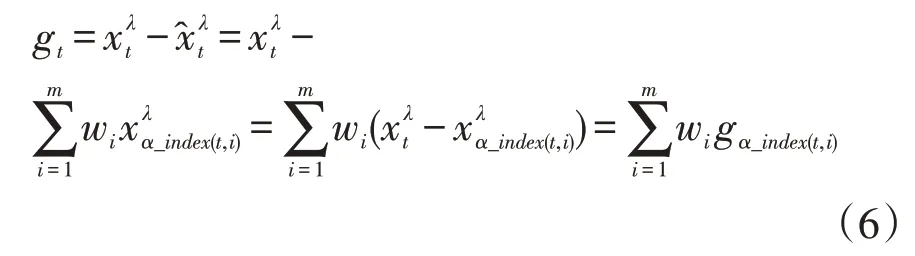
樣本期內基于GIOWA 算子的組合預測λ次冪誤差平方和為：

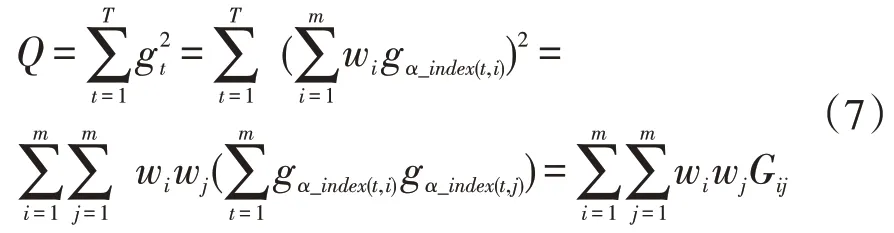
Gm=(Gij)m×m為GIOWA 組合預測λ次冪誤差信息矩陣，表示為：

所以，使得GIOWA組合預測模型的λ次冪誤差平方和達到最小值來確定最優權重w1,w2,…,wm，可建立的組合預測優化模型為：

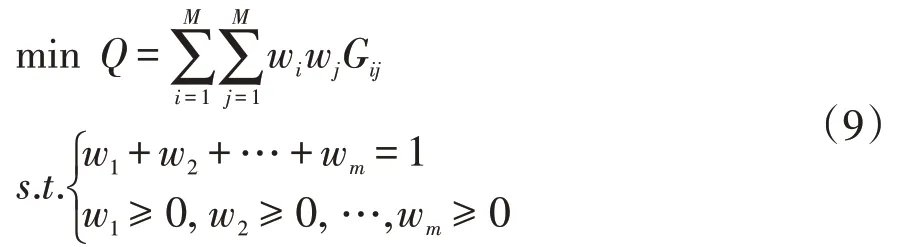
最后，在誤差平方和最小為最優性準則之下建立λ=1，λ=-1，λ→0，λ=0.5 和λ=0.25 的不同參數值的誘導有序加權組合預測模型。

2.2 GIOWA組合預測模型

（1）當λ=1 時的廣義誘導有序加權平均（GIOWA）組合預測模型

當λ=1 時，廣義誘導有序加權平均（GIOWA）組合預測模型就是誘導有序加權算術平均（IOWA）組合預測模型。

取m=3,T=30，則對應的（8）式的誘導有序誤差信息矩陣為：

使預測誤差平方和最小的IOWA 組合預測模型：

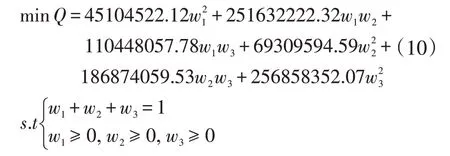
可以利用LINGO.10 軟件求得權重為w1=0.6356,w2=0.3644,w3=0，得到IOWA 組合預測模型為：

求得目標函數值即此模型的誤差平方和：Q=33253220。

（2）當λ= -1 時廣義誘導有序加權平均（GIOWA）組合預測模型

當λ= -1時，廣義誘導有序加權平均（GIOWA）組合預測模型就是誘導有序加權調和平均（IOWHA）組合預測模型，對誘導有序預測數據取倒數誤差，最終通過求解權重，建立的IOWHA組合預測模型為：

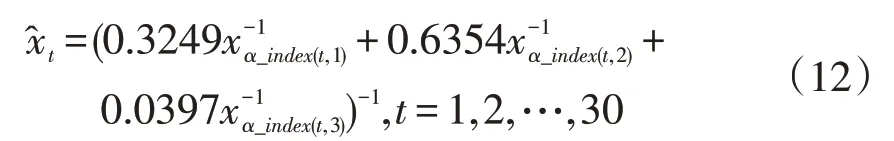
求得目標函數值即此模型的倒數誤差平方和：Q=1.688335×10-10。

（3）當λ→0 時廣義誘導有序加權平均（GIOWA）組合預測模型

當λ→0 時，廣義誘導有序加權平均（GIOWA）組合預測模型就是誘導有序加權幾何平均（IOWGA）組合預測模型，對誘導有序預測數據取對數誤差，最終建立誤差平方和最小的IOWGA組合預測模型為：

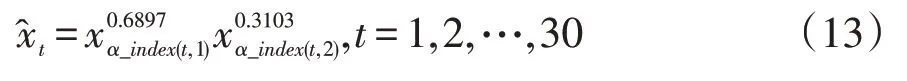
求得目標函數值即此模型的對數誤差平方和為Q=1.457986×10-2。

（4）當λ=0.5 和λ=0.25 時廣義誘導有序加權平均（GIOWA）組合預測模型

分別對誘導有序預測數據取其0.5次冪誤差和0.25 次冪誤差，最終所建立的GIOWA（λ=0.5）、GIOWA（λ=0.25）組合預測模型分別為：

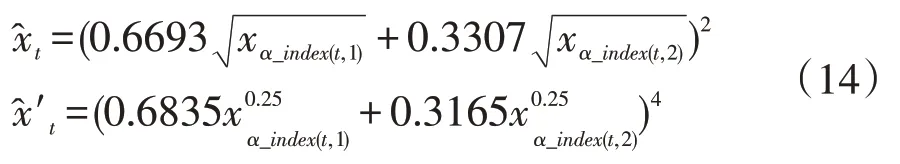
所對應的誤差平方和分別為86.233和0.1168。

λ取不同值時，廣義誘導有序加權平均組合預測模型的預測值見表5。

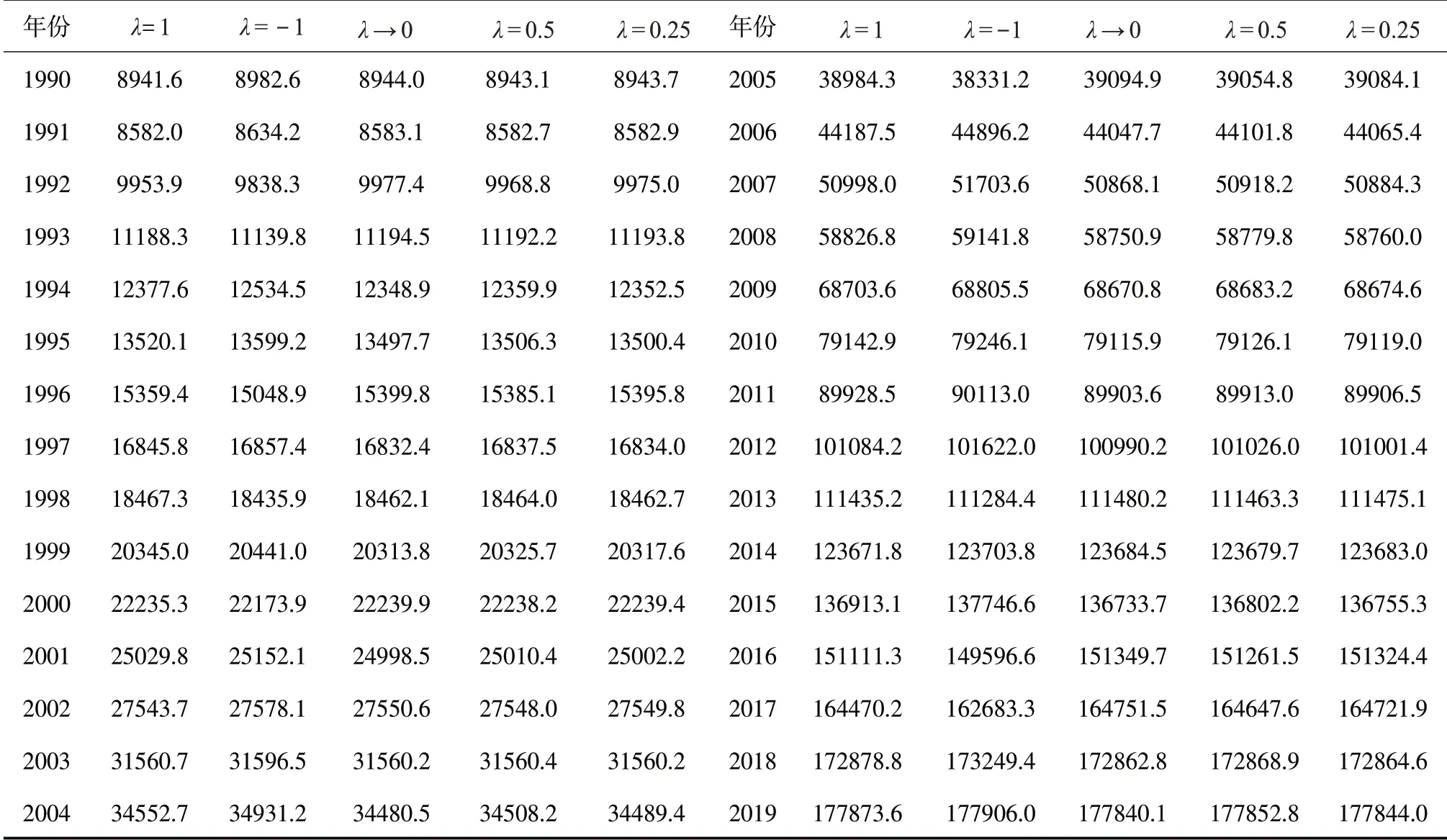
表5 不同λ 時的GIOWA組合預測值（億元）

將表5 的組合預測結果進行可視化，為了對不同λ取值的組合預測數據進行更加直觀地比較，將λ=1，λ= -1，λ→0，λ=0.5 和λ=0.25 的不同參數值的誘導有序加權組合預測值分別在前者的基礎上向上平移1×104個單位，觀察其預測趨勢。由圖1可以看出當λ取不同值時各個組合預測趨勢相近，預測值非常接近，各個組合預測結果沒有明顯差異，且都與真實值有相同的趨勢。

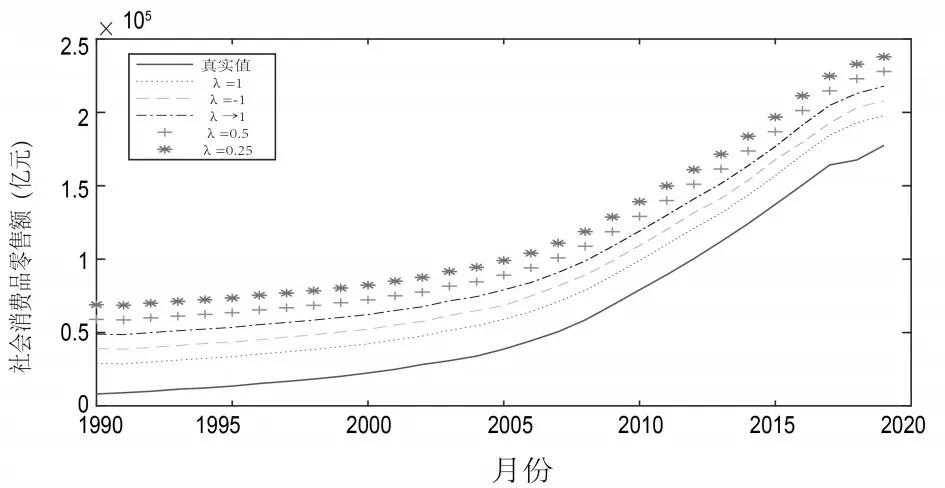
圖1 不同λ值時組合預測結果

2.3 預測模型評價

選擇平方和誤差（SSE）、均方根誤差（RMSE）和平均絕對誤差（MAE）作為預測模型誤差的評價指標，并對評價指標進行歸一化處理，再分別對各個預測方法在1990-2019年的預測值的平均精度進行比較。

由表6 可知，當λ=1，λ= -1，λ→0 ，λ=0.5和λ=0.25 時的GIOWA 組合預測模型的平方和誤差（SSE）、均方根誤差（RMSE）以及平均絕對誤差（MAE）均小于各個單項預測的誤差，平均精度也都在0.98 以上，均大于各個單項預測的平均精度，說明本文建立的組合預測模型在單項預測模型的基礎上進一步提高了預測精度，具有較好的預測效果。因此，可以運用λ取不同參數值的GIOWA組合預測模型對我國2020-2024年的社會消費品零售額進行預測。

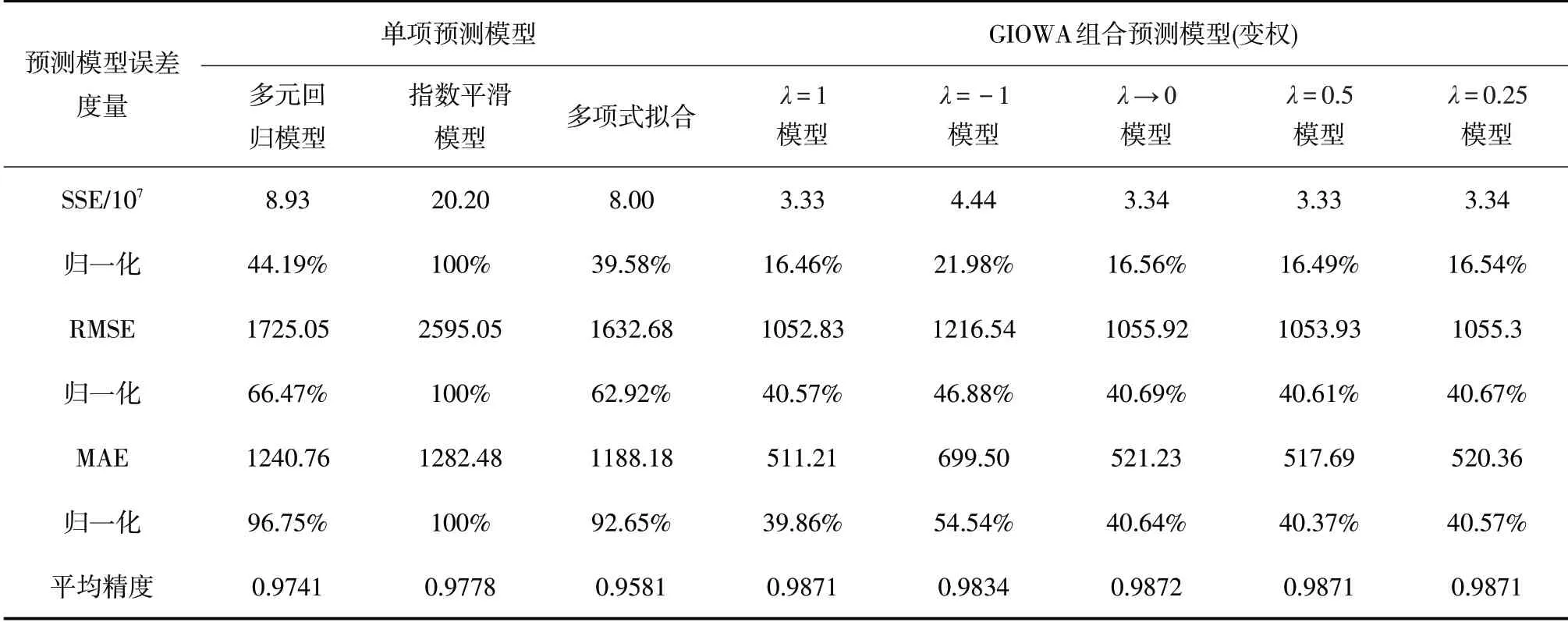
表6 預測模型評價體系（基于1990-2019年預測數據）

2.4 λ 取不同值的GIOWA組合預測模型的預測

組合預測模型以精度作為誘導值，得出不同精度對應預測值的組合權重，本文再利用簡單平均法得到多元線性回歸、Holt-Winters 非季節指數平滑以及多項式擬合3 種單項預測方法在預測期的權重，如表7所示。

表7 三種單項預測方法的組合權重

因此，通過對三種單項預測方法的2020-2024年的預測值賦予權重，可對我國2020-2024 年的社會消費品零售額進行更高精度的預測，預測結果見表8。由表8可以看出，五種組合預測的預測值非常接近，未來五年我國社會消費品零售總額整體呈現上升趨勢，消除價格因素后的實際同比增長率會有所下降，五種組合預測模型預測出的2020-2024 年社會消費品零售總額的增長率分別為：5.1%，4.7%，4.5%，4.2%和3.9%。

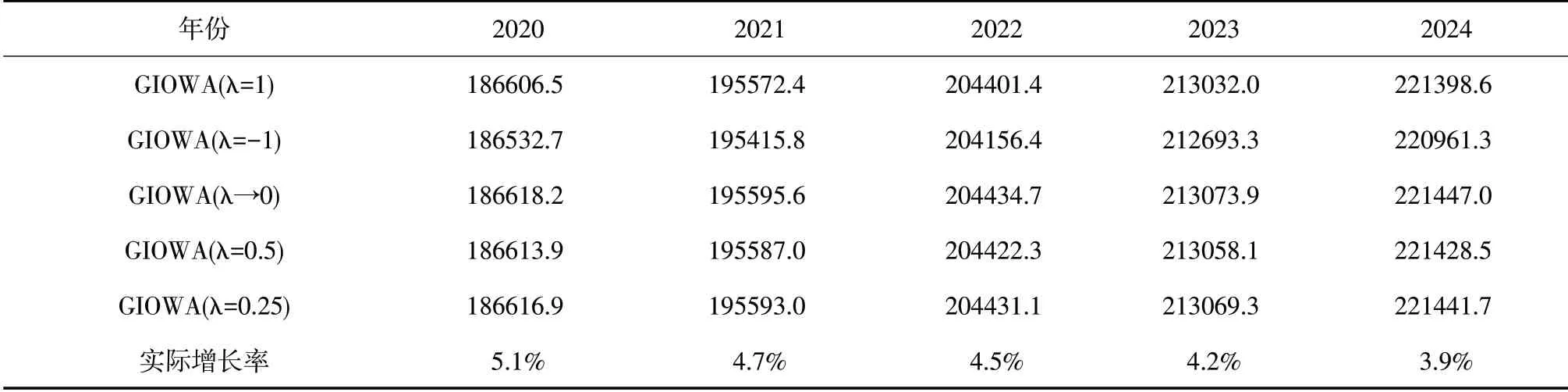
表8 2020—2024年我國實際社會消費品零售總額組合預測結果（億元）

3 總結

首先分別采用多元線性回歸模型、Holt-Winters非季節指數平滑模型以及多項式擬合對我國2020-2024年的社會消費品零售總額進行單項預測，然后分別建立以單項預測精度為誘導值，以誤差平方和最小為最優模型準則的λ取不同參數值的GIOWA組合預測模型，并構建了誤差評價體系，結果表明基于GIOWA 算子的組合預測精度高于各個單項預測精度，從而提高了我國社會消費品零售額預測的精度。

通過對我國社會消費品零售額的組合預測建模分析，預測未來5 年我國社會消費品零售額有明顯增長趨勢，2020-2024 年的實際同比增長率分別為：5.1%，4.7%，4.5%，4.2%和3.9%。扣除價格因素后通過對我國社會消費品零售總額的預測，可以一定程度上反映我國未來5年的居民消費狀況。社會消費品零售總額的持續增長，說明未來我國居民的消費潛力將持續釋放，雖然2020年上半年疫情的爆發為居民帶來收入和消費的不穩定因素，但是疫情的有效防控為接下來幾年的居民消費質量和消費數量的增加提供了發展條件。目前消費已經成為我國經濟走上高質量發展的重要引擎力量之一，應積極優化消費環境，大力發展消費經濟，發展更多利民便民、促進居民消費的新模式，創造更多發展動能，促進我國經濟的高質量發展。