基于HRRP序列的空間進動目標參數估計方法

查 林，陳大慶，吳 鵬

(1．中國電子科技集團公司第三十八研究所，安徽合肥 230088；2．太原衛星發射中心技術部，山西太原 036301；3.中國人民解放軍32086部隊，北京 100000)

0 引言

中段防御是導彈防御的關鍵階段，因為它具有防御面積大、攔截時間長、彈道相對固定[1]的優點。然而當導彈在中段釋放誘餌后，由于彈頭、誘餌、殘骸、假目標等組成包含真假目標的威脅目標群，并且以大致相同的速度和軌跡在大氣層外做慣性飛行，很難用軌跡和速度上的差別來區分各目標；此外，其他各種先進突防手段的采用，也使得中段攔截導彈在目標識別上面臨極大的挑戰，這已經成為彈道導彈防御系統發展的一個瓶頸。但是由于彈頭目標的特殊結構在特定的受力作用下會產生微動，所謂微動是指目標或目標的組成部分除了質心平動以外的振動、轉動、翻滾和加速運動等微小運動。因為此運動狀態常常是獨一無二的，反映了目標的精細特征，所以可以用來作為目標識別的重要依據。因此，很多學者提出利用中段目標的微動特征來區分真假彈頭[2-13]，微動參數估計的主要途徑[2]有基于時頻圖[3]、ISAR(Inverse Synthetic Aperture Radar)圖像[4-5]、RCS(Radar Cross Section)[6-7]、高分辨距離像[8-14]等。

雷達高分辨距離像包含了目標徑向的空間結構信息[15]，在雷達光學區內能夠較好地描述目標的散射特性，在彈道中段，因受彈頭進動的影響[16-17]，由多幅連續高分辨距離像構成的一維距離像序列上的散射中心位置將會發生周期性走動，其包含著目標的進動調制信息，因此可利用目標的一維距離像序列來估計目標的進動參數和形狀參數。文獻[8-13]以錐體目標為研究對象，其中文獻[8]在利用目標一維距離像序列變化估計進動參數過程中需要已知目標的一些結構參數，而這些參數實際中是很難獲取的；文獻[9-10]利用散射中心在雷達視線上投影距離之間的相關性實現目標進動特征的提取；文獻[11]對目標散射中心的一維投影距離進行建模，采用非線性擬合的方法估計進動和結構參數；文獻[12-13]通過雷達視角的變化來實現目標進動特征的提取，其中文獻[12]從時間-距離像數據實現錐體彈頭散射點三維空間位置的重構，并在此基礎上進行目標進動特征的提取，文獻[13]利用多視角觀測一維距離像序列聯合獲得彈道目標各個散射中心的絕對坐標；文獻[14]以旋轉對稱錐柱體目標為研究對象，基于靜態電磁散射數據，利用雷達觀測視角內錐柱體各散射中心的一維距離像序列中各散射中心間的相對位置變化的極值與目標參數之間的關系來進行目標進動和結構參數的估計，不過僅從區域Ⅱ(α<β<π/2)進行考慮，且在參數估計過程中未考慮參數耦合問題。

本文從寬帶雷達體制出發，以錐體目標為研究對象，針對缺少目標結構參數等先驗信息及估計過程中參數耦合問題，基于高分辨距離測量提出了一種能同時估計出空間錐體目標進動參數和形狀參數的方法，仿真表明該方法可行、有效。文中第二部分對錐體目標的進動模型進行分析，得出目標姿態角隨時間變化的關系式，進而得出目標徑向長度序列與姿態角關系式；第三部分對如何從回波信號中提取徑向長度序列作了詳細介紹；第四部分給出了本方法的具體實現步驟及推導過程；第五部分通過仿真計算驗證了該方法的可行性和有效性。

1 錐體目標進動模型

彈道導彈的彈頭外形一般較常見的有平底錐彈頭、球底錐彈頭、平底錐柱彈頭及球底錐柱彈頭4種，本文主要對平底錐彈頭進行分析，其結構如圖1所示，其中α為目標半錐角，b為目標斜邊長度，R為底面半徑，1、2、3表示彈頭目標的3個散射中心。

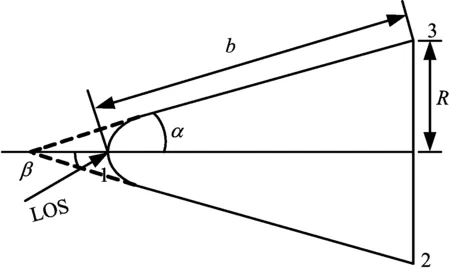
圖1 錐體目標結構圖

在彈道導彈飛行過程中，為了保證飛行的平穩性和命中的精度，彈頭目標會采用自旋的方式定向，而在誘餌釋放、彈箭分離時，彈頭目標不可避免地會受到橫向擾動，進而產生進動，稱為微動。由于誘餌、假目標、殘骸等其他空間目標無姿態控制系統，故不會具有規律的微動特性。彈頭目標的規律微動特性導致姿態角，即雷達視線與目標自旋軸的夾角，呈現周期變化。姿態角的變化規律同目標的進動參數有關，但是姿態角一般不易直接測量得到。另一方面，如果不考慮目標的平動，姿態角的周期變化會導致空間進動錐體目標的徑向長度序列呈現規律變化，其變化規律同錐體目標的形狀參數和進動參數有關，其中，某次觀測中錐體目標的徑向長度序列，是指通過該次觀測中的各次回波計算出的錐頂散射中心和錐底散射中心的徑向距離的差值，并由這些差值組成的序列。因此可以利用彈頭目標特有的微動特性來提取彈頭目標的進動參數和形狀參數。

根據以上分析，可建立彈道中段錐體目標進動模型[9]如圖2所示，Oxcyczc坐標系為平動坐標系，Oxsyszs坐標系為隨體坐標系，彈頭繞其對稱軸Ozs以角速度Ω作自旋運動，同時軸Ozs繞軸Ozc以角速度ω進動，進動角為θ，故zs為自旋軸，zc為進動軸，γ為雷達視線與進動軸夾角，即俯仰角，ω為進動角頻率，β為雷達視線與自旋軸夾角，即姿態角，LOS是指雷達視線方向。根據圖2所示的錐體目標的進動模型，可以得到第k次觀測錐體目標的姿態角隨時間t變化的表達式為

βk(t)=arccos[cosθkcosγk+

sinθksinγkcos(ωt+φk)]

(1)

式中，γk為第k次觀測的俯仰角，θk為第k次觀測的進動角，φk為第k次觀測的進動初相角，k=1,2。

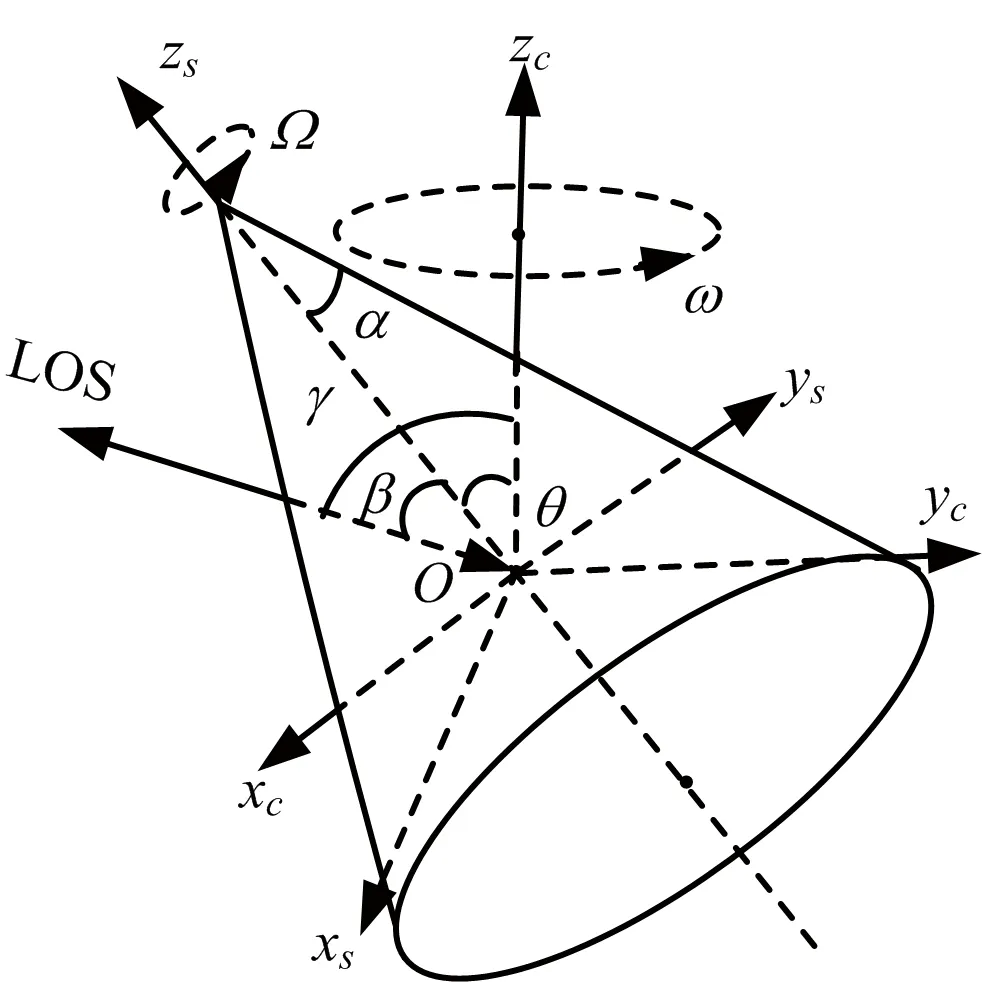
圖2 錐體目標進動模型

實際雷達探測目標時一般迎著錐頂照射錐體目標，且錐形彈頭和誘餌的半錐角較小，一般取 5°～15°，此時可認為錐體目標進動時姿態角β< π-α，在這一角度范圍內，鈍頭錐對應散射中心1與2均一直可見[9]。根據上述姿態角隨時間變化的表達式，可以求出第k次觀測中錐體目標的徑向長度序列的表達式為

Lk(n)=bcos(βk(tkn)+α)

(2)

式中，tkn表示第k次觀測第n個回波的時刻，n=1,2,…,N，N為每次觀測的回波數目。

2 徑向長度序列提取

當目標運動速度不高時，可以認為在一個脈沖持續時間內，目標到雷達站的距離不變，即所謂的“停-跳”假設；但對于高速機動目標，如導彈目標，上述假設不再成立，此時應當首先估計每次觀測時目標的軌道運動信息。令第k次觀測中第i個回波時，目標到雷達站距離的表達式為

Rki(t)=Rki0+fki(t)

(3)

式中，Rki0為參考時刻目標距雷達站的距離，fki(t)為第k次觀測第i個回波中目標的軌道運動表達式。下面對所獲得的寬帶回波信號進行平動補償，具體方法如下：

令第k次觀測中第i個回波對應的雷達發射信號的表達式為

ski(t)=pki(t)ej2πf0t=|pki(t)|ejφki(t)ej2πf0t

(4)

式中，k=1,2，i=1,2,…,N，f0為載頻，c為電磁波的傳播速度，pki(t)為發射信號的復包絡，|pki(t)|為pki(t)的幅度，φki(t)為pki(t)的相位，|·|表示求模運算。則該次回波信號解調后的表達式為

srki(t)=Apki(t-τki(t))e-j2πf0τki(t)=

A|pki(t-τki(t))|ejφki(t-τki(t))e-j2πf0τki(t)

(5)

式中，τki(t)=2Rki(t)/c，A為該次回波信號的幅度。將目標到雷達站的距離表達式代入式(5)，則該次回波的表達式可以寫作：

srki(t)=Apki(t-τki(t))e-j2πf0τki(t)=

A|pki(t-τki(t))|ejφki(t-τki(t))·

e-j2πf0τki(t)=

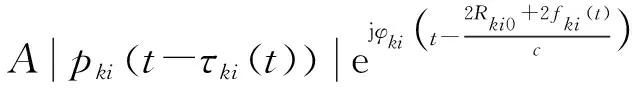
A|pki(t-τki(t))|ejφki1(t)·

(6)

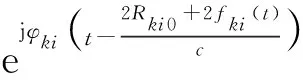
(7)

至此，完成了對寬帶回波信號的平動補償，下面依次對各信號用MUSIC算法[16]作參數估計，提取強散射中心的距離，并形成散射中心距離歷程圖(一維距離像序列)，其中，散射中心距離歷程圖是指橫坐標為各次回波的時刻，縱坐標為各次回波中強散射中心的距離的圖像。然后運用圖像邊緣檢測方法[17]，從散射中心距離歷程圖提取各次回波時刻錐頂散射中心和錐底散射中心的徑向距離的差值，這些差值組成的序列即為錐體目標的徑向長度序列，并將第一次觀測的徑向長度序列記為L1(n)，第二次觀測的徑向長度序列記為L2(n)，其中，n=1,2,…,N。

3 參數估計

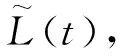
l1max=bcos[(γ1+α)-θ]=

bcos(γ1+α)cosθ+bsin(γ1+α)sinθ

(8)

l1min=bcos[(γ1+α)+θ]=

bcos(γ1+α)cosθ-bsin(γ1+α)sinθ

(9)

l2max=bcos[(γ2+α)-θ]=

bcos(γ2+α)cosθ+bsin(γ2+α)sinθ

(10)

l2min=bcos[(γ2+α)+θ]=

bcos(γ2+α)cosθ-bsin(γ2+α)sinθ

(11)

進一步有以下關系成立：

l1max+l1min=2bcos(γ1+α)cosθ

(12)

l1max-l1min=2bsin(γ1+α)sinθ

(13)

l2max+l2min=2bcos(γ2+α)cosθ

(14)

l2max-l2min=2bsin(γ2+α)sinθ

(15)

為進一步推導方便，令a11=l1max+l1min，a12=l1max-l1min，a21=l2max+l2min，a22=l2max-l2min。所以有

(a11sinθ)2+(a12cosθ)2=4b2sin2θcos2θ

(16)

(a21sinθ)2+(a22cosθ)2=4b2sin2θcos2θ

(17)

因此可以解得

(18)

(19)

(20)

l1max=bcos[(θ+α)-γ1]=

bcos(θ+α)cosγ1+bsin(θ+α)sinγ1

(21)

l1min=bcos[(γ1+α)+θ]=

bcos(θ+α)cosγ1-bsin(θ+α)sinγ1

(22)

l2max=bcos[(θ+α)-γ2]=

bcos(θ+α)cosγ2+bsin(θ+α)sinγ2

(23)

l2min=bcos[(θ+α)+γ2]=

bcos(θ+α)cosγ2-bsin(θ+α)sinγ2

(24)

進一步有以下關系成立：

l1max+l1min=2bcos(θ+α)cosγ1

(25)

l1max-l1min=2bsin(θ+α)sinγ1

(26)

l2max+l2min=2bcos(θ+α)cosγ2

(27)

l2max-l2min=2bsin(θ+α)sinγ2

(28)

為進一步推導方便，令a11=l1max+l1min，a12=l1max-l1min，a21=l2max+l2min，a22=l2max-l2min。所以有

[a11sin(θ+α)]2+[a12cos(θ+α)]2=

4b2sin2(θ+α)cos2(θ+α)

(29)

[a21sin(θ+α)]2+[a22cos(θ+α)]2=

4b2sin2(θ+α)cos2(θ+α)

(30)

因此可以解得

(31)

(32)

(33)

(34)

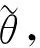
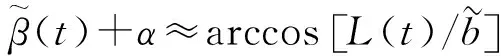
(35)

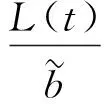
(36)

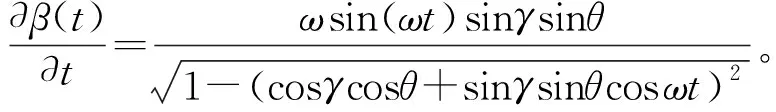
(37)

令x=cosωt，則有

(38)

以下來分析h的變化規律：

1) 當x=±1，即ωt=kπ時，h取最小值0。

2) 下面分析h何時取得極大值。根據求極值原理可知當h對x的一階偏導為0時h可以取得極大值。

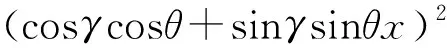
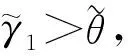
(39)

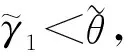
(40)

至此，我們完成了對目標進動角、半錐角及斜邊長度的估計，其計算流程如圖3所示。

4 仿真與分析

實驗所觀測的錐體目標如圖1所示，其形狀參數為：目標半錐角α=14°，目標斜邊長度b=1 m，底面半徑R=0.25 m；進動參數為：進動角θ=10°，進動角頻率ω=31.4 rad/s。第一次觀測的俯仰角γ1=37°，第二次觀測的俯仰角γ2=37.2°。實驗所用數據為空間進動錐體目標電磁仿真數據，測量頻帶為9～11 GHz，頻點間隔為0.02 GHz。假定目標回波中的觀測噪聲為高斯白噪聲，觀測信噪比SNR的定義為

(41)

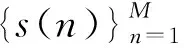
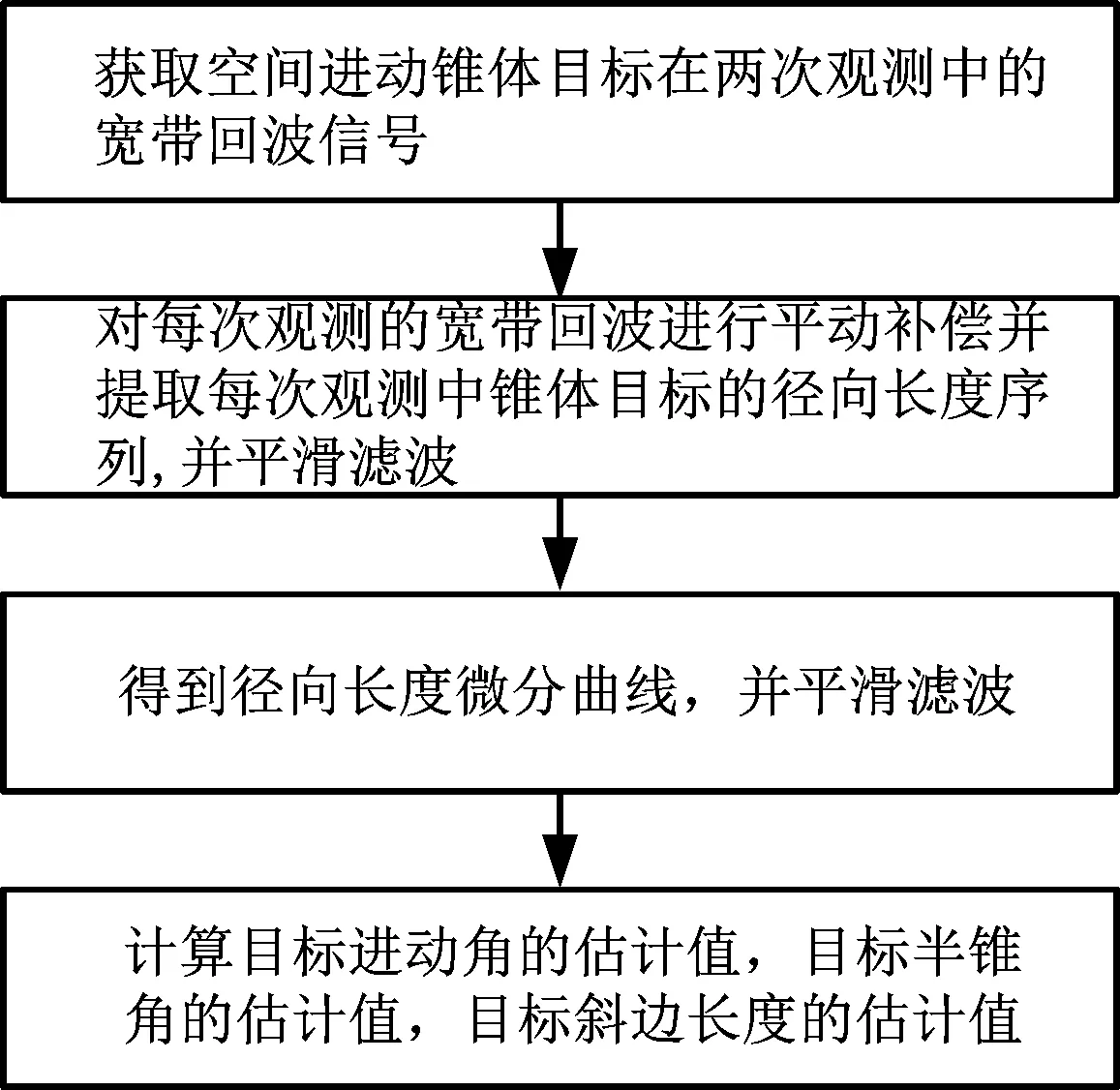
圖3 方法流程圖

首先在觀測信噪比20 dB條件下進行仿真實驗，得如下結果：圖4(a)為第一次觀測所得的目標錐頂、錐底散射中心的一維距離像序列，圖4(b)為第二次觀測所得的目標錐頂、錐底散射中心的一維距離像序列，圖4(c)、(d)分別為第一、二次觀測所得的錐體目標徑向長度序列。從圖中可以看出，散射點對應的一維距離像序列與徑向長度序列均呈正弦規律變化，且頻率一致，這與前述分析一致，故可通過這種規律性變化來進行目標形狀和進動參數估計；另外，從圖中還可以看出此時所得的徑向長度序列曲線有毛刺，并且信噪比越低，毛刺越多，即抖動越大，這是因為信噪比較低時，距離估計精度比較差。圖5以第一次觀測為例，給出了不同信噪比條件下目標徑向長度序列曲線。

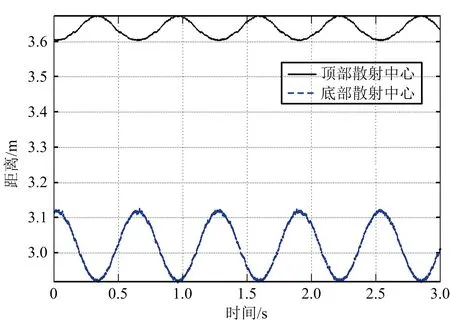
(a) 第一次觀測得到的散射中心一維距離像序列

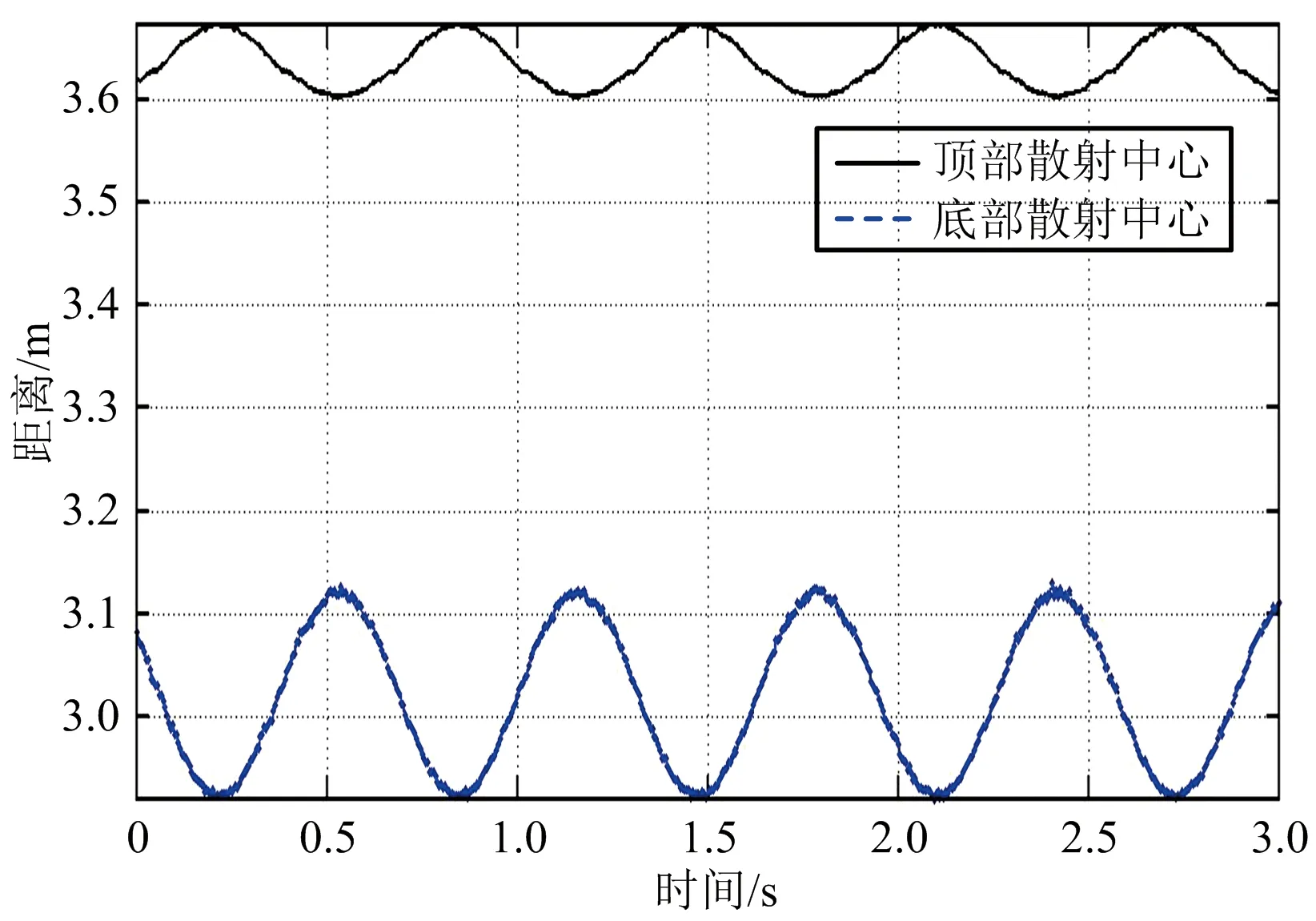
(b) 第二次觀測得到的散射中心一維距離像序列

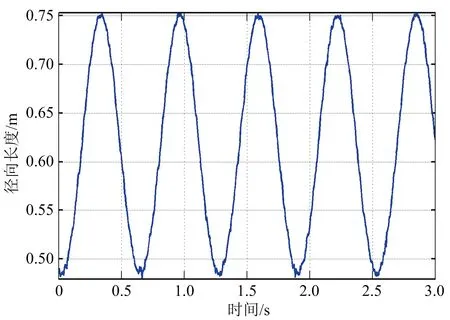
(c) 第一次觀測得到的徑向長度序列

(d) 第二次觀測得到的徑向長度序列圖4 錐體目標一維距離像及徑向長度序列

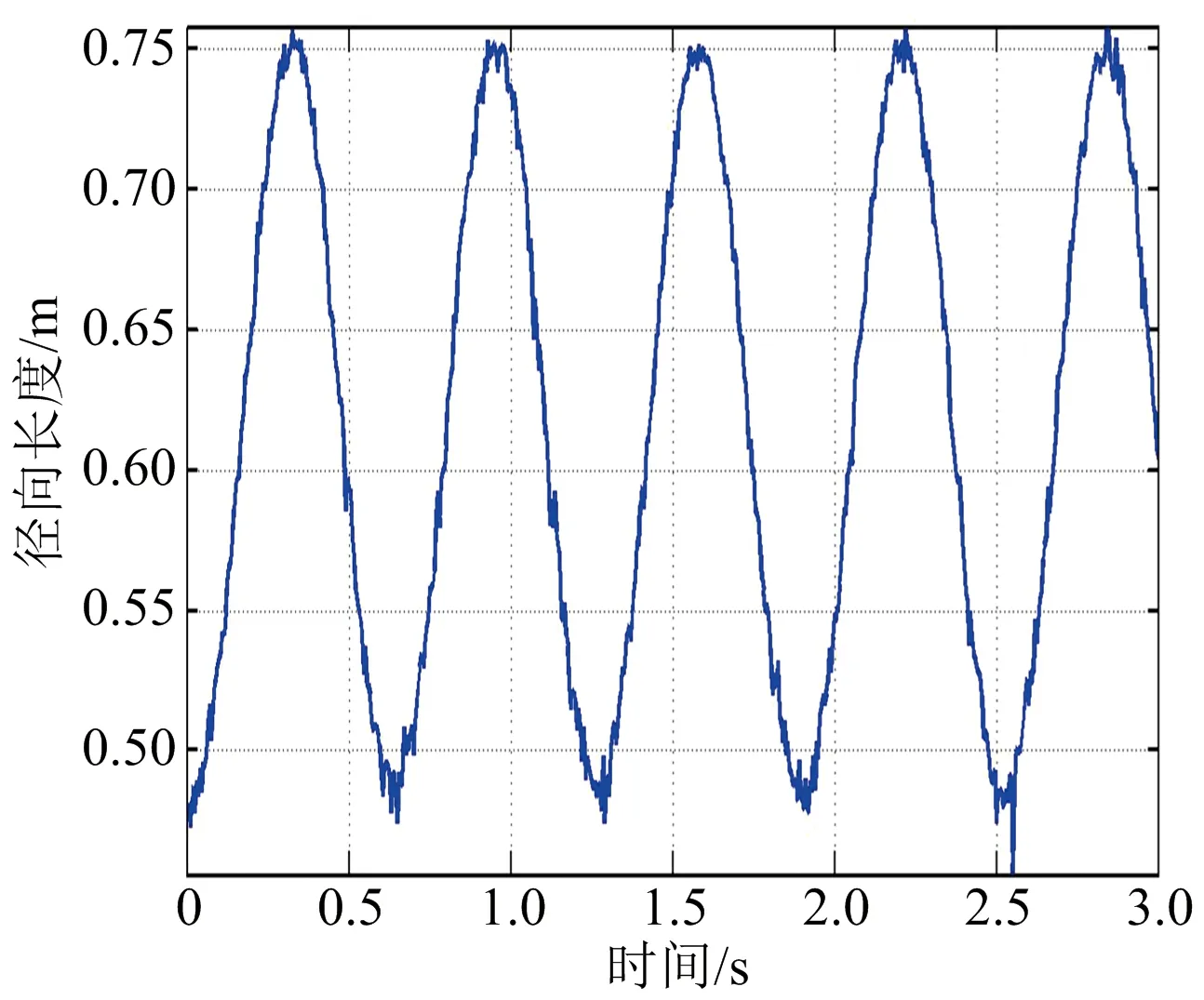
(a) SNR=15 dB

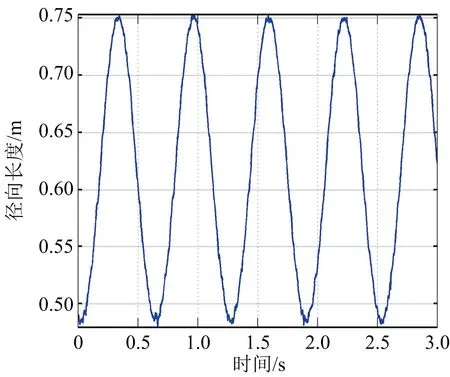
(b) SNR=20 dB

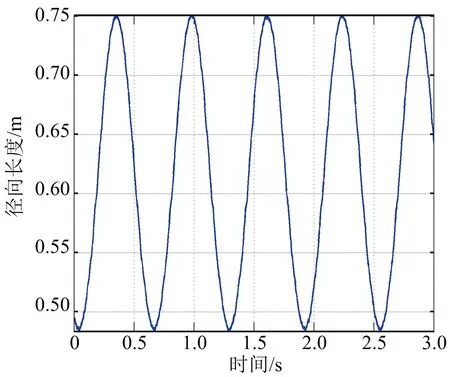
(c) SNR=25 dB圖5 不同信噪比下的徑向長度序列曲線

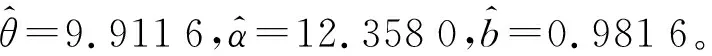
(a) 第一次觀測得到的平滑濾波后的徑向長度距離曲線

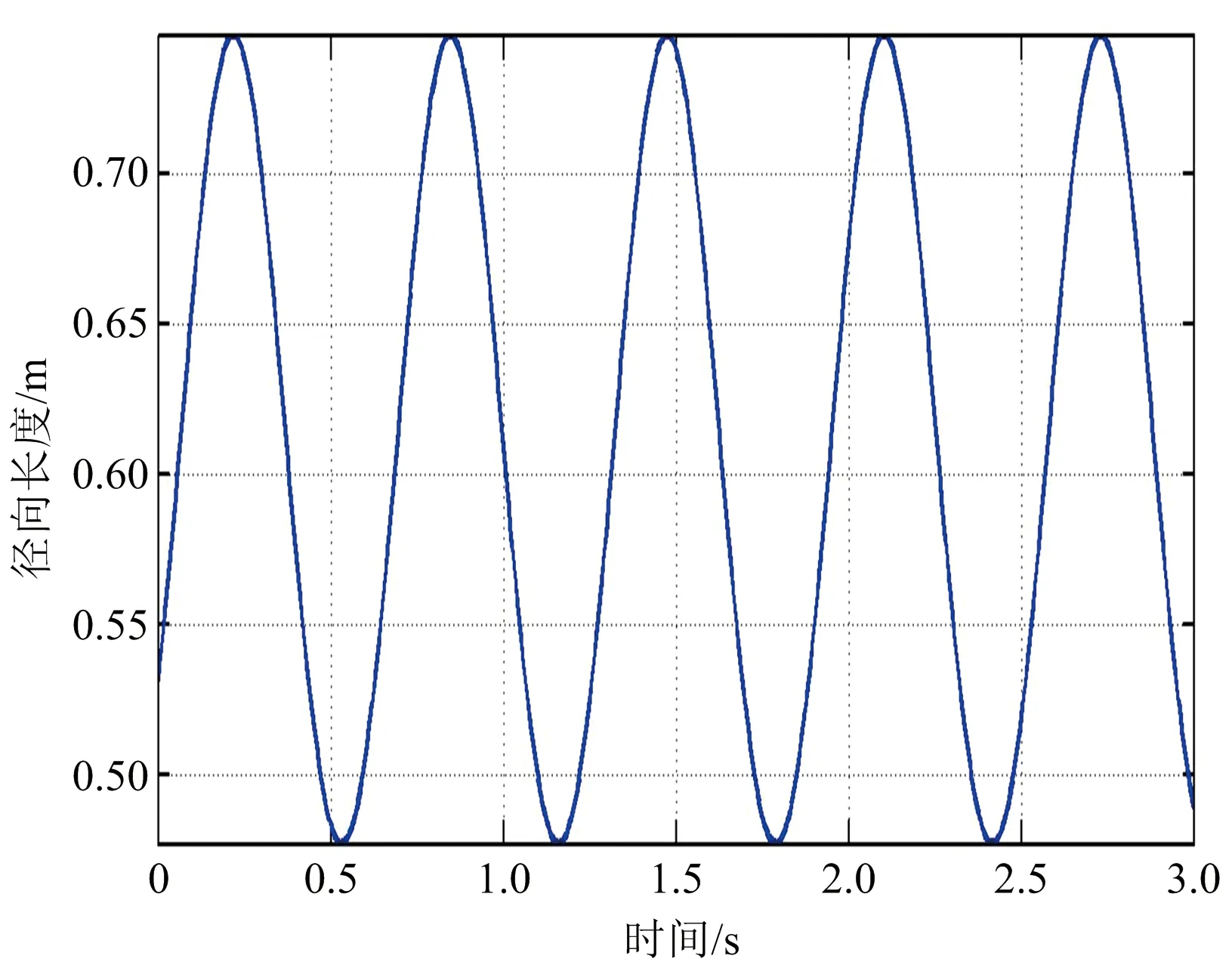
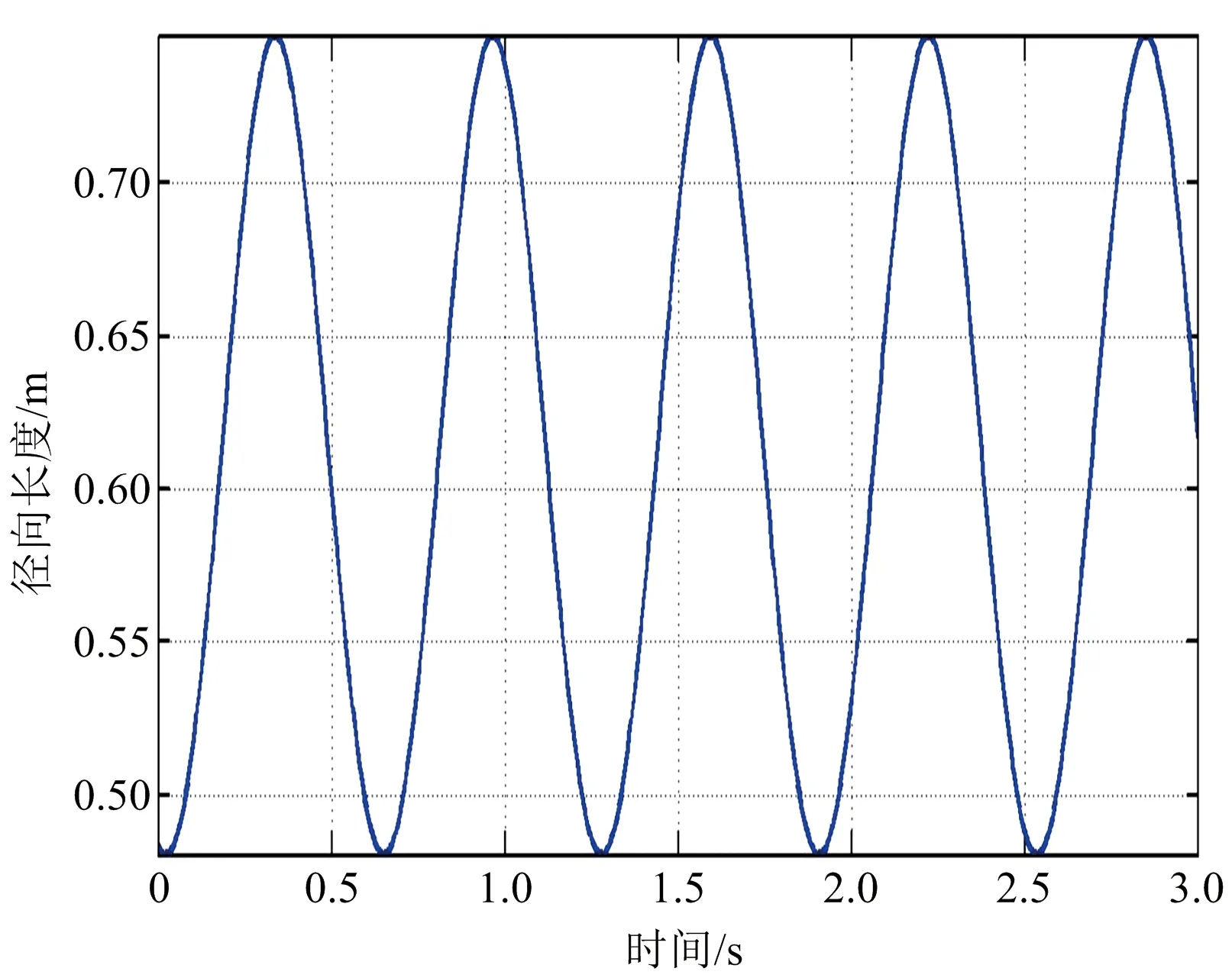
(b) 第二次觀測得到的平滑濾波后的徑向長度距離曲線圖6 平滑濾波后的徑向長度序列曲線

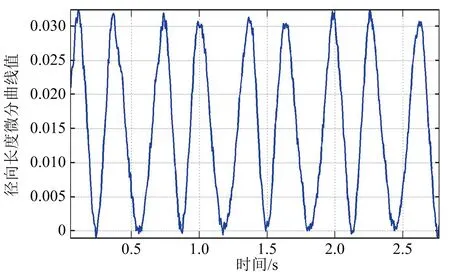
(a) 錐體目標徑向長度微分曲線

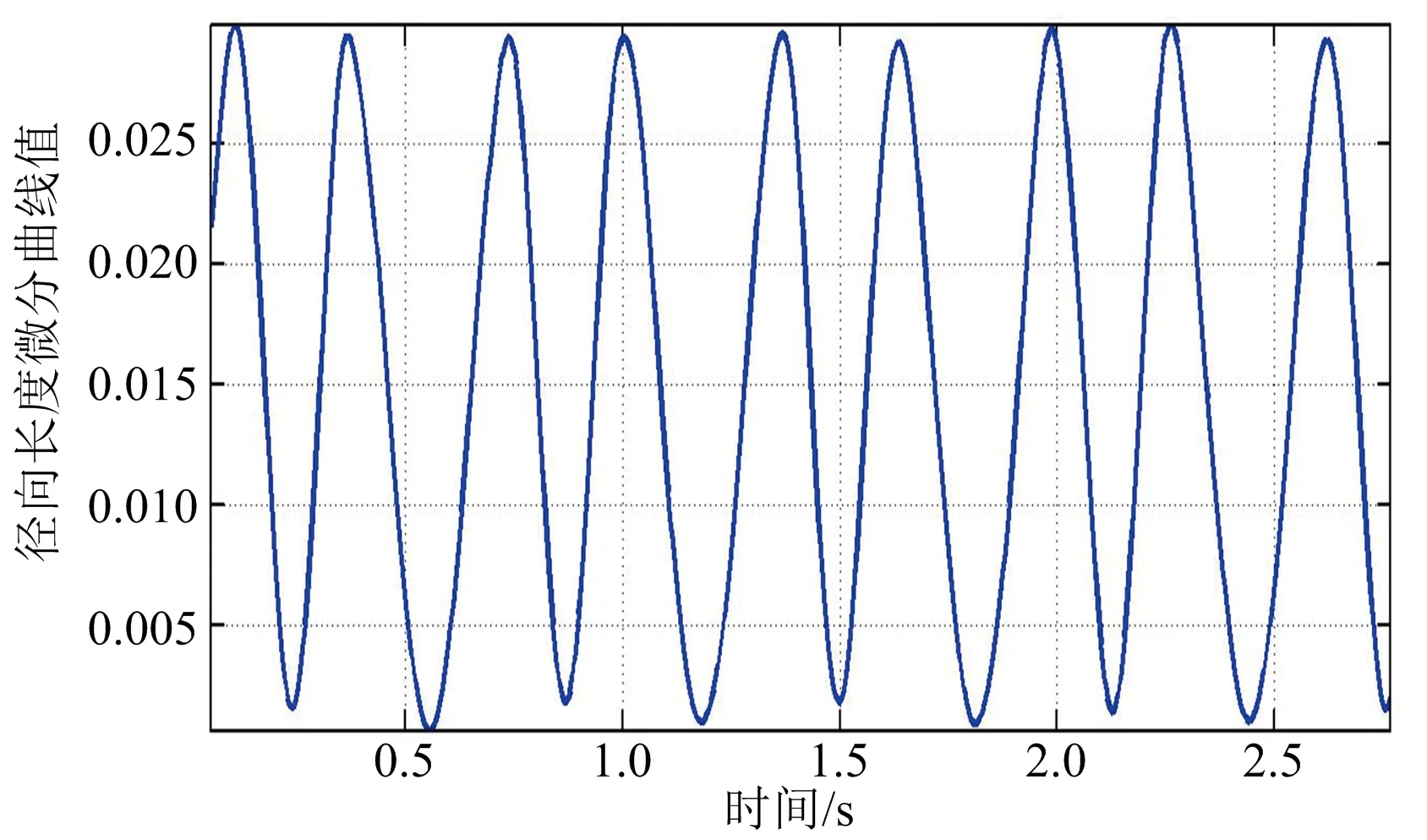
(b) 平滑濾波后的錐體目標徑向長度微分曲線圖7 錐體目標徑向長度微分曲線

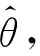
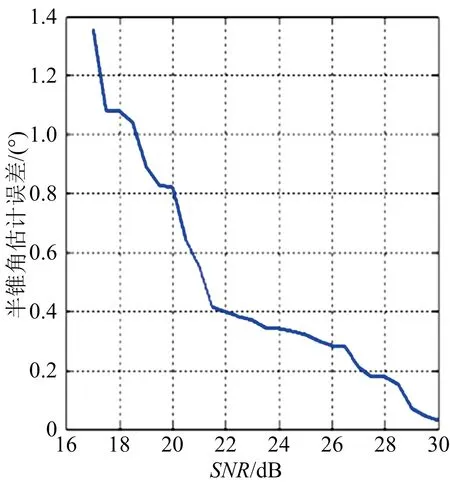
圖9 半錐角估計誤差

圖10 斜邊長度的估計誤差

5 結束語

本文從寬帶雷達體制出發，以空間錐體目標為研究對象，針對缺少目標結構參數等先驗信息及估計過程中參數耦合問題，通過對其進動模型的分析，根據錐頂和錐底散射中心徑向距離變化曲線，利用點散射中心間相對位置的極值變化信息，提出一種基于高分辨距離測量的中段彈道導彈目標進動參數和形狀參數估計方法，并給出了詳細推導步驟，仿真結果表明此方法可以同時估計出空間進動錐體目標的形狀參數和進動參數；另外，該方法充分利用了空間進動錐體目標的徑向長度序列、進動參數和形狀參數的關系，且不使用非線性曲線擬合的方法估計目標的進動參數，從而提高了參數估計方法的可實施性，改善了參數估計過程的穩定性。