La摻雜ZnO的電子結(jié)構(gòu)和光學性質(zhì)的第一性原理

張 蕾,王海芳,劉曉慶,安 寧,王星星

(中北大學環(huán)境與安全工程學院,太原 030051)

ZnO是一種新型的Ⅱ-VI族直接禁帶半導體材料,在常溫常壓下的禁帶寬度為3.37 eV,激子束縛能為60 meV[1-3],具有介電常數(shù)低、光學耦合系數(shù)大、化學穩(wěn)定性高、光電性能優(yōu)良等優(yōu)點[4-5]。稀土元素具有獨特的電子結(jié)構(gòu)和豐富的分離能級,摻雜后能使ZnO材料的s-p態(tài)與摻雜元素的d態(tài)之間發(fā)生交換耦合,導致材料的電子、光學和磁性能的劇烈變化[6-8]。因此,稀土元素通過有效摻雜使得ZnO的電子結(jié)構(gòu)和光學性質(zhì)得到一定程度上的改善,從而使材料在光電器件中具有良好的應用前景。

在理論計算方面,Li等[9]研究了有無空位的La摻雜對ZnO(0001)-Zn極性表面磁性的影響,發(fā)現(xiàn)La摻雜容易在ZnO表面上產(chǎn)生Zn空位,其誘導兩個未配對的O-2p電子在同一方向旋轉(zhuǎn)產(chǎn)生凈磁矩。Li等[10]研究了La摻雜和Zn空位共存于ZnO體系時,體系具有鐵磁性。最接近Zn空位中的Zn-4s、Zn-3p、O-2p和La-5s軌道間存在強雜化耦合電子交換效應。Li等[11]研究了稀土元素(RE=La,Er,Nd)摻雜的ZnO納米粉末,發(fā)現(xiàn)在La摻雜后費米能級向上移動進入導帶呈現(xiàn)n型半導體。摻雜體系的光電性質(zhì)主要受La-6s軌道電子的影響。Peng等[12]研究了La摻雜對ZnO光電性質(zhì)的影響,發(fā)現(xiàn)隨著La摻雜量的增加,ZnO的帶隙變寬,吸收系數(shù)降低,可見光范圍反射率降低,吸收邊緣發(fā)生藍移。

對于La摻雜ZnO的第一性原理計算主要在電子結(jié)構(gòu)和磁性研究,光學性質(zhì)研究較少。現(xiàn)應用第一性原理對不同La摻雜量的ZnO電子結(jié)構(gòu)和光學性質(zhì)進行系統(tǒng)地計算研究,以期為提高La摻雜ZnO的光電性能和相關(guān)光學器件的設計提供理論依據(jù)。

1 理論模型和計算方法

1.1 理論模型

理想的ZnO晶體是六方纖鋅礦結(jié)構(gòu),屬于P63/mc空間群,具有C6v-4對稱性[13]。晶格常數(shù)a=b=3.249 ?,c=5.206 ?,α=β=90°,γ=120°。所有計算均基于2×2×2 ZnO超胞,共包含16個Zn原子和16個O原子。設計兩種摻雜超胞模型:Zn0.937 5La0.062 5O和Zn0.875La0.125O。Gou等[14]采用了5種不同的摻雜位置研究Fe-In共摻雜ZnO。因此,對Zn0.875La0.125O的超胞模型設計5種摻雜配置。兩個La原子分別取代0和1、0和2、0和3、0和4、0和5處的兩個Zn原子。超胞模型如圖1所示。

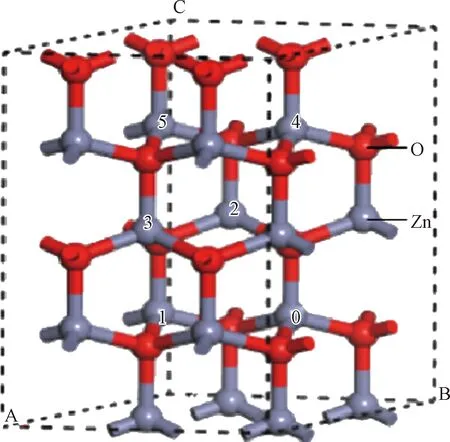
灰色球體代表Zn原子,紅色球體代表O原子圖1 ZnO(2×2×2)超胞模型Fig.1 Supercell model of ZnO (2×2×2)

1.2 計算方法

采用CASTEP(Materials Studio2017)中的密度泛函理論框架下的廣義梯度近似平面波超軟贗勢[15]方法,用Perdew-Burke-Ernzerhof泛函描述電子間的交換-關(guān)聯(lián)能[16]。不考慮自旋極化效應,在倒易空間中對所有超胞模型進行幾何結(jié)構(gòu)優(yōu)化和能量計算。優(yōu)化時,平面波截斷能設為430 eV,能量的收斂精度設為1×10-5eV/atom,作用在每個原子上的力不大于0.03 eV/?,內(nèi)應力不大于0.05 GPa,公差偏移設為0.001 ?。采用4×4×4的k點網(wǎng)格對布里淵區(qū)求和。用于構(gòu)建贗勢的價電子組態(tài)分別為Zn 3d104s2、O2s22p4、La5s25p65d16s2。在幾何結(jié)構(gòu)優(yōu)化基礎上,對所有模型的電子結(jié)構(gòu)和光學性質(zhì)進行計算,最后對結(jié)果進行分析和討論。

2 結(jié)果與討論

2.1 晶體結(jié)構(gòu)和穩(wěn)定性分析

Zn1-xLaxO (x=0,0.062 5,0.125) 模型進行幾何結(jié)構(gòu)優(yōu)化后的晶格參數(shù)a、c,晶胞體積V,形成能Ef和La-La原子間距R如表1所示。計算結(jié)果表明,與未摻雜ZnO相比,由于La(1.06 ?)[17]的離子半徑比Zn(0.74 ?)[18]大,且因替位摻雜使La3+離子多余正電荷之間相互排斥作用增大,上述兩者的共同作用使得摻雜體系的晶胞體積隨著La摻雜量的增加而增大。與此同時,晶胞體積隨著La-La原子間距的增加而增大。

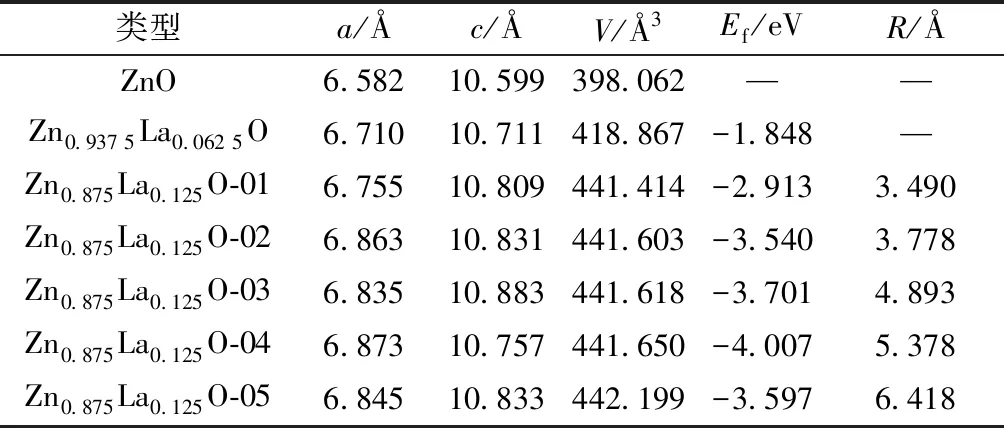
表1 Zn1-xLaxO(x=0,0.062 5,0.125)優(yōu)化后的晶格參數(shù)Table 1 The optimized lattice parameters of Zn1-xLaxO (x=0,0.062 5,0.125)

形成能是表征摻雜體系穩(wěn)定性和原子摻入體系難易程度的物理變量。基于La-La原子間距優(yōu)化后的體系總能量和不同原子的化學勢計算的形成能表明,隨著La摻雜量增加,體系形成能減小,摻雜更容易,結(jié)構(gòu)更穩(wěn)定。此外,與其他摻雜結(jié)構(gòu)相比,Zn0.875La0.125O-04的形成能是最小的,說明相應的結(jié)構(gòu)在能量上是最穩(wěn)定的,在實驗中更容易獲得。因此在以下分析中,對于12.5%的摻雜結(jié)構(gòu),僅考慮Zn0.875La0.125O-04模型。

2.2 態(tài)密度分析

Zn1-xLaxO(x=0,0.062 5,0.125)模型的態(tài)密度分布如圖2(a)～圖2(c)所示。圖2(a)顯示未摻雜ZnO的價帶分為3個區(qū)域:上價帶主要來自 O-2p 態(tài)的貢獻,下價帶主要來自Zn-3d態(tài)的貢獻。在-6.6～0 eV范圍內(nèi),Zn-3d和O-2p態(tài)之間具有較強的雜化作用,形成了較強的鋅氧鍵。在-18.5～-15.9 eV范圍內(nèi),來自O-2s態(tài)的貢獻。導帶部分主要由Zn-3p、Zn-4s和O-2p態(tài)組成。圖2(b)、圖2(c)所示La摻雜后費米能級向上移動進入導帶,轉(zhuǎn)化為n型半導體。價帶由4個區(qū)域組成:第1個峰位于-33.4 eV附近,來自La-5s和La-6s態(tài)的貢獻；第2個峰位于-21.2～-18.5 eV,來自La-5p和O-2s態(tài)的貢獻,表明這兩種態(tài)具有強雜化作用；第3個峰位于-16.8 eV附近,來自La-5p和O-2s態(tài)的貢獻；第4個峰位于-8.6～-2.1 eV,來自Zn-3d和O-2p態(tài)的貢獻。La-5d態(tài)主要貢獻于 2.4 eV 左右的導帶,使得導體中出現(xiàn)了一個強局域態(tài)。因此增加了導帶的電子態(tài)密度,使得電子態(tài)發(fā)生簡并,費米能級上移進入導帶。此外,隨著La摻雜量的增加,價帶中的峰值稍有減小,表明陽離子和陰離子的雜化程度降低,說明La摻雜ZnO體系的共價性質(zhì)隨著La摻雜量的增加而降低。

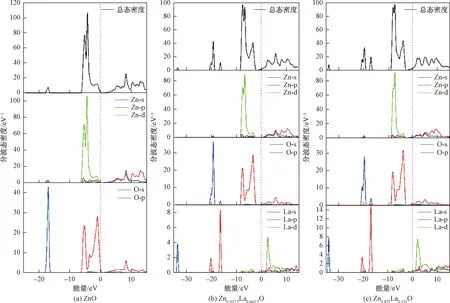
圖2 Zn1-xLaxO(x=0,0.062 5,0.125)態(tài)密度分布Fig.2 The density of states of Zn1-xLaxO(x=0,0.062 5,0.125)

2.3 布居值和鍵長分析

布居值用于分析成鍵后的鍵型變化,反映原子周圍的電子群分布[19]。Zn1-xLaxO(x=0,0.062 5,0.125)模型的布居值和鍵長如表2所示。由表2可知,比較摻雜過程中其他未與摻雜原子直接連接的Zn、O原子間的Zn—O鍵發(fā)現(xiàn),各摻雜體系的最長Zn—O鍵的布居值呈逐漸減小的趨勢,鍵長逐漸增加,說明其共價性逐漸減弱。摻雜體系中最短 Zn—O 鍵的布居值和鍵長變化都不明顯。同一摻雜體系的最長Zn—O鍵的布居值都比最短Zn—O鍵的布居值小,最長Zn—O鍵與最短Zn—O鍵的布居值比例隨La摻雜量的增加而減小,說明La摻入對體系的晶格畸變有很大的影響,這個趨勢與體積的變化類同。摻雜后,La—O鍵的布居值低于Zn—O鍵,原因是La(1.10)的電負性低于Zn(1.65),導致在成鍵時O原子更容易從La原子中獲得電子,因此La—O鍵的極性較強。通過鍵能計算可知,La—O鍵的鍵能比Zn—O鍵大,離子鍵更強。此外,隨著La摻雜量的增加,平行于和垂直于c軸方向的 La—O 鍵布居值減少且鍵長增加,這是由于La3+替換Zn2+使多余正電荷之間相互排斥作用增大,導致La3+和O2-離子的雜化作用減小。結(jié)果表明,隨著La摻雜量的增加,La—O原子周圍電子云重疊減少,共價性減弱,離子性增強。

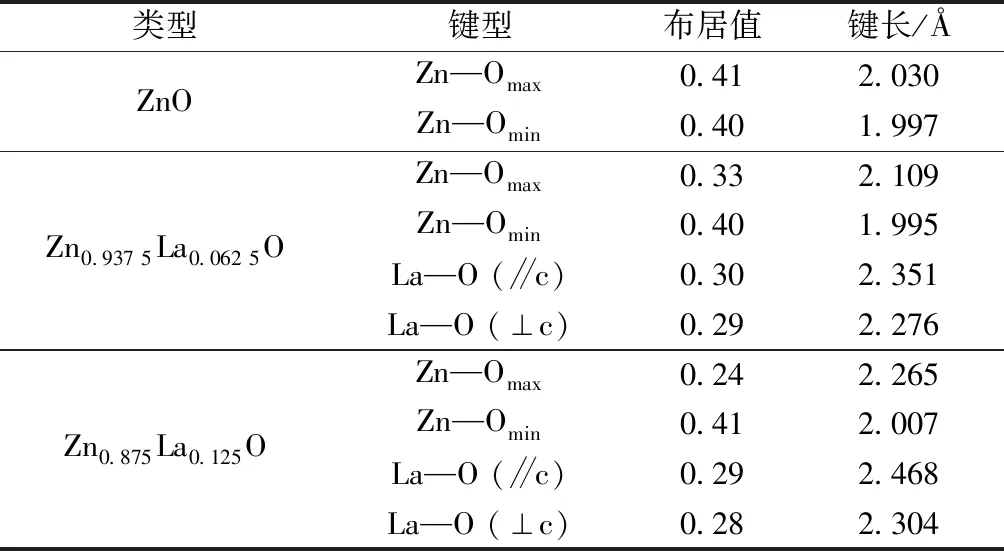
表2 Zn1-xLaxO的布居值與鍵長(x=0,0.062 5,0.125)Table 2 Mulliken bond population and bond length of Zn1-xLaxO (x=0,0.062 5,0.125)

2.4 光學性質(zhì)分析

材料的介電函數(shù)反映了能帶結(jié)構(gòu)和光躍遷之間的信息。Zn1-xLaxO(x=0,0.062 5,0.125)模型的介電函數(shù)虛部如圖3所示。未摻雜ZnO的虛部主要有3個峰:第1個峰位于1.76 eV,由價帶最高處的O-2p態(tài)和導帶最低處的Zn-4s態(tài)之間的光學躍遷引起；第2個峰位于6.46 eV,由Zn-3d和O-2p態(tài)之間的光學躍遷引起；第3個峰位于10.09 eV,由O-2s和Zn-3d態(tài)之間的光學躍遷引起。摻La后的兩個虛部曲線,在19.11 eV附近出現(xiàn)了一個新峰,這主要是由價帶中La-5p態(tài)電子躍遷到導帶底所致。同時,Zn0.875La0.125O在0.71 eV附近出現(xiàn)新峰,這是由位于-8.68～-2.89 eV的La-5d態(tài)的電子帶內(nèi)躍遷所得,而在Zn0.937 5La0.062 5O體系中沒有觀察到這個峰值。此外,由于La的摻入影響了位于16.51 eV、19.43 eV附近的O-2s態(tài)電子,使得隨著La摻雜量的增加,在6.48 eV附近的峰略微向高能量方向移動且峰值強度增強,而在10.07 eV附近的峰向低能量方向移動且峰值強度減弱。

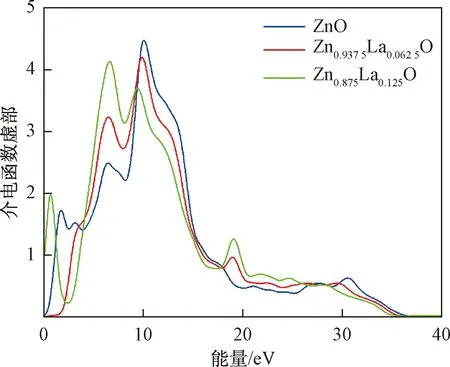
圖3 介電函數(shù)虛部Fig.3 Imaginary part of the dielectric function

吸收系數(shù)反映了體系的光吸收能力。Zn1-xLaxO(x=0,0.062 5,0.125)模型的吸收系數(shù)如圖4所示。通過分析1.3～4.0 eV范圍內(nèi)的吸收系數(shù),發(fā)現(xiàn)La的摻入引起光學吸收邊的藍移,其原因是La摻入后作為施主原子引入高濃度的載流子(電子),使費米能級移入導帶而產(chǎn)生Burstein-Moss效應引起的。同時,Zn0.875La0.125O體系在1.08 eV出現(xiàn)新峰,原因是由La原子d-d軌道的電子帶內(nèi)躍遷所致。3條曲線的主要吸收峰出現(xiàn)在13.73 eV附近,處于真空紫外區(qū),且隨著La摻雜量的增加,吸收峰出現(xiàn)紅移和峰值強度減弱的現(xiàn)象。此外,位于30.94 eV附近的峰出現(xiàn)紅移且強度弱于未摻雜ZnO,原因是由位于19.37 eV的La-5p軌道中的電子躍遷所致。

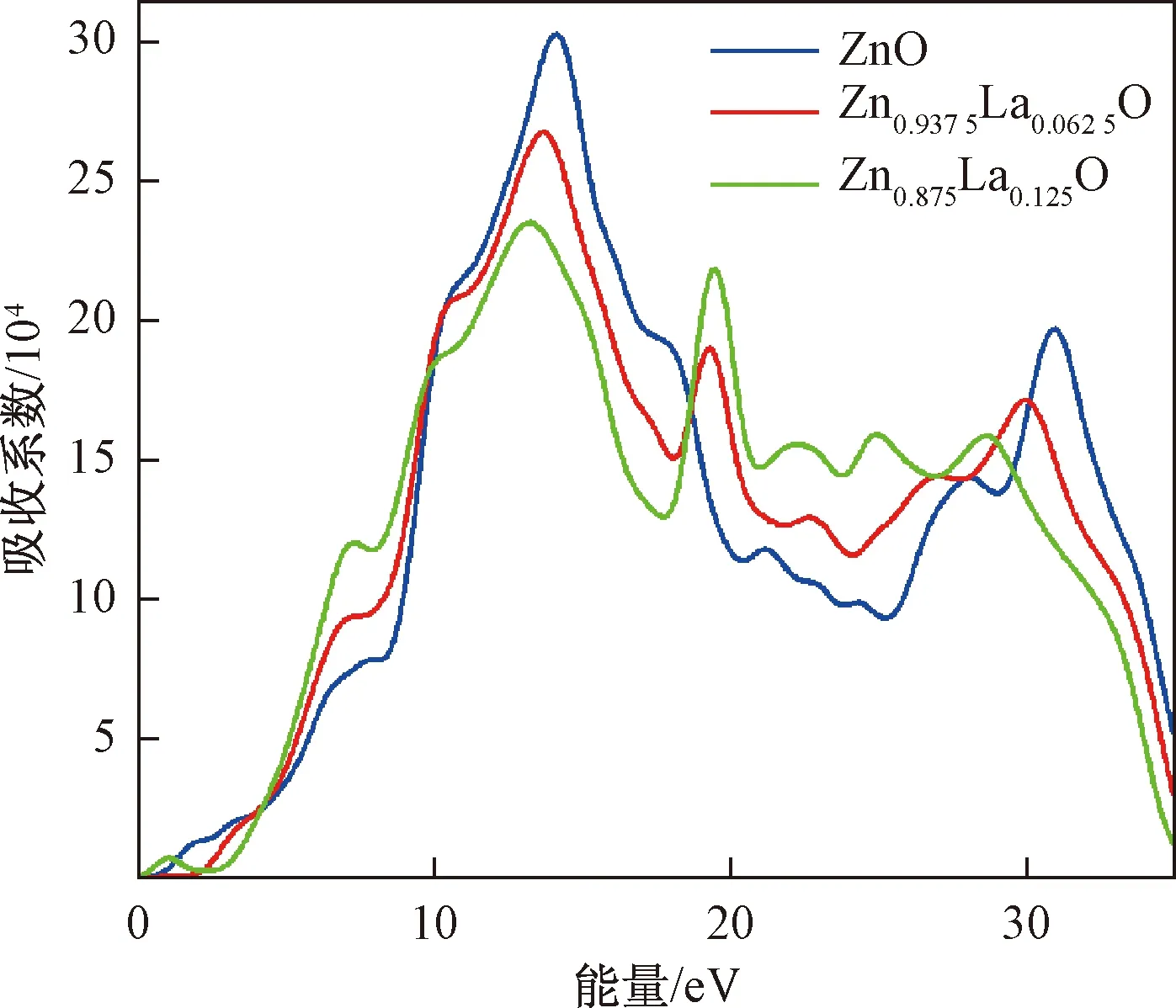
圖4 吸收系數(shù)Fig.4 Absorption coefficient

能量損失函數(shù)反映了光子穿過晶體時的能量損失。Zn1-xLaxO(x=0,0.062 5,0.125)模型的能量損失函數(shù)如圖5所示。未摻雜ZnO的主峰位于19.23 eV,這與理論計算值一致。對于La摻雜ZnO結(jié)構(gòu),在16.32 eV附近存在峰,且強度較弱于未摻雜ZnO體系。此外,隨著La摻雜量的增加,位于32.11 eV附近的峰發(fā)生明顯的紅移且峰值強度減弱。

3 結(jié)論

采用第一性原理密度泛函理論,研究了La(0,0.062 5,0.125)摻雜ZnO的電子結(jié)構(gòu)和光學性質(zhì)的影響。計算后得到以下結(jié)論。

(1)隨著La摻雜量和La-La原子間距的增加,摻雜體系的晶胞體積增大,形成能減少。La—O鍵的布居值減少,鍵長增加,La3+和O2-離子的雜化作用減弱,共價性減弱,離子性增強,鍵能增加,體系的穩(wěn)定性增強。

(2)電子結(jié)構(gòu)計算表明,La摻雜后費米能級向上移動進入導帶,呈現(xiàn)為n型半導體。

(3)光學性質(zhì)計算表明,La摻雜引起位于可見光區(qū)的吸收邊發(fā)生藍移,是由于產(chǎn)生Burstein-Moss效應所致。在低能區(qū)出現(xiàn)新的吸收峰,其源自La原子的d-d軌道的帶內(nèi)電子躍遷。在真空紫外區(qū),由于La-5p軌道上的電子躍遷,使高能區(qū)的峰發(fā)生紅移且隨著La摻雜量的增加峰值強度減弱。能量損失峰向低能方向移動,能量損失峰值強度明顯減少。