算術平均的正弦與正切平均確界的改進*
楊 月 英
(湖州職業(yè)技術學院 機電與汽車工程學院, 浙江 湖州 313000)
一、研究背景
2015年,Witkowski介紹了正弦平均Msin(a,b)和正切平均Mtan(a,b):
(1)
并證明了不等式
Mtan(a,b) 對所有a,b>0且a≠b成立,其中A(a,b)=(a+b)/2是兩個正數(shù)a和b的算術平均[1]1 071-1 092. 最近,許多學者研究了正弦平均Msin(a,b) 和正切平均Mtan(a,b) ,發(fā)現(xiàn)了許多重要的不等式[1]1 071-1 092 [2]1-11 [3]23-32 [4]383-392. Nowicka和Witkowski證明了不等式 (2) α2Msin(a,b)+(1-α2)Mtan(a,b) (3) 對所有a,b>0且a≠b,當且僅當α1≤2/3,β1≥0.719 6L,α2≤0.655 1L和β2≥2/3成立[4]383-392. 根據(jù)不等式(2)和(3)可推得 (4) 對所有a,b>0且a≠b成立. 本文的研究目的是加細不等式(4),得到最佳參數(shù)λ和μ使得雙向不等式 對所有a,b>0且a≠b成立. 為證明本文的主要結果,需要以下2個引理: 也在(a,b)內單調上升(下降);如果f′(x)/g′(x)的單調性是嚴格的,則結論中的單調性也是嚴格的[5]10. 引理2函數(shù) 在區(qū)間(0,1)內是嚴格單調上升的且值域為: 證明對函數(shù)φ(x)求導,可得: (5) 其中, φ1(x)=-x2[2cos3(x)+4cos2(x)+5cos(x)+1]+ (6) 應用冪級數(shù)展開式 可得: (7) (8) 從等式(6)和不等式(7)(8)使得 (9) 對所有x∈(0,1)成立. 根據(jù)等式(5)和不等式(9)可得函數(shù)φ(x)在區(qū)間(0,1)內單調上升.注意到: (10) 所以引理2容易從等式(10)和函數(shù)φ(x)的單調性得到. 下面證明本文的主要結果. 定理1雙向不等式 對所有a,b>0且a≠b成立,當且僅當λ≤4/5,μ≥0.838 6L. 證明由于正弦平均Msin(a,b)、正切平均Mtan(a,b)和算術平均A(a,b)都是對稱且一階齊次的,不失一般性,假設a>b>0.設x=(a-b)/(a+b)∈(0,1),則從等式(1)可得: (11) 從等式(11)可得: (12) (13) 簡單計算可得: f1(0+)=f2(0)=0,f(x)=f1(x)/f2(x), (14) (15) (16) 作為定理1的應用,可以得到如下推論1(Jordan不等式): 推論1設λ≤4/5和μ≥0.838 6L,則雙向不等式 對所有x∈(0,1)成立.二、主要結果
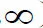
xsin(x)[3cos2(x)+4cos(x)+2]+sin2(x)cos(x)[cos(x)+2].


