FIR濾波器設(shè)計(jì)的最小二乘方法研究
張壽安 張靜雅
(1.六安職業(yè)技術(shù)學(xué)院信息與電子工程學(xué)院 安徽六安 237000;2.皖西學(xué)院電子與信息工程學(xué)院 安徽六安 237000)
一、引言
伴隨著計(jì)算機(jī)電子技術(shù)與集成電路技術(shù)的不斷更新,采用數(shù)字濾波器處理數(shù)字信號(hào)已經(jīng)成為現(xiàn)代電子數(shù)字系統(tǒng)的發(fā)展主流[1]。其中FIR(有限長(zhǎng)單位沖激響應(yīng))濾波器是備受企業(yè)與科研人員關(guān)注的熱點(diǎn),其設(shè)計(jì)方法有很多,例如窗函數(shù)法、頻率選擇法、最優(yōu)設(shè)計(jì)法等。屈召貴利用窗函數(shù)法對(duì)離散信號(hào)的數(shù)字代碼進(jìn)行運(yùn)算處理,實(shí)現(xiàn)改變信號(hào)頻譜的技術(shù)應(yīng)用[2]。夏利霞等人采用了粒子群優(yōu)化算法實(shí)現(xiàn)了濾波器頻率特性的優(yōu)化,與遺傳算法相比具有更快的收斂速度[3]。為實(shí)現(xiàn)FIR濾波器參數(shù)的優(yōu)化通常采用MATLAB工具進(jìn)行仿真模擬。例如蔣夢(mèng)影等人比較了程序設(shè)計(jì)法、FDATool設(shè)計(jì)法與SPTool設(shè)計(jì)法的性能,具有較強(qiáng)的實(shí)用性[4]。但是不能精確的控制濾波器通帶阻帶的頻率,導(dǎo)致設(shè)計(jì)出來的濾波器在實(shí)際應(yīng)用中存在很大的阻礙。然而,杜林等人采用約束最小二乘法進(jìn)行FIR數(shù)字濾波器設(shè)計(jì),在MATLAB仿真結(jié)果表明最小二乘法顯示更強(qiáng)大的生命力與實(shí)用性[5]。本文利用MATLAB工具箱設(shè)計(jì)濾波器,根據(jù)對(duì)比設(shè)計(jì)要求和理想的濾波器性能,不斷調(diào)整參數(shù)使得濾波器的設(shè)計(jì)變得更加直觀簡(jiǎn)便,工作量較小,也有利于達(dá)到濾波器設(shè)計(jì)的最優(yōu)解。
二、基于最小二乘法的FIR濾波器設(shè)計(jì)原理
(一)FIR濾波器的基本結(jié)構(gòu)。FIR濾波器的頻率響應(yīng)在時(shí)域上為有限長(zhǎng)度,結(jié)構(gòu)主要包括橫截型和級(jí)聯(lián)型。
1.FIR濾波器的橫截型結(jié)構(gòu)。FIR濾波器系統(tǒng)的輸入輸出的方程為:
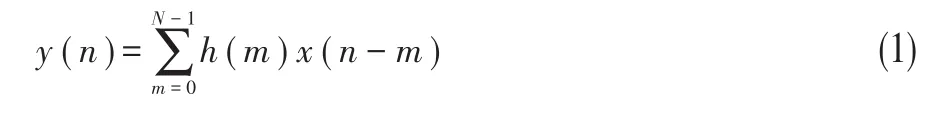
由以上方程直接實(shí)現(xiàn)得到的濾波器如圖1:
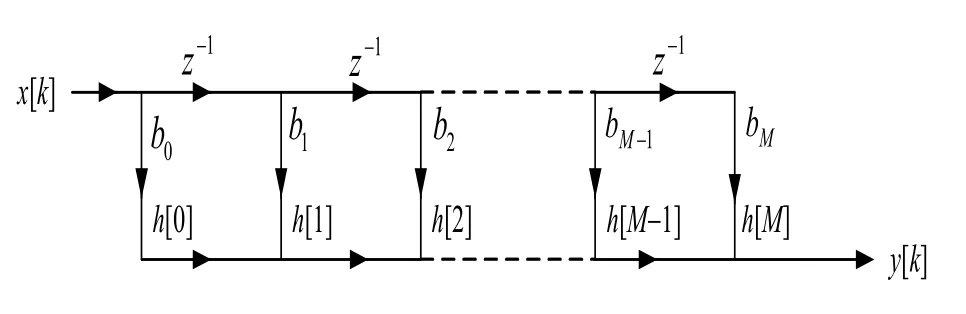
圖1 FIR濾波器的橫截型結(jié)構(gòu)
2、FIR濾波器的級(jí)聯(lián)型結(jié)構(gòu)。將H(z)分解成實(shí)系數(shù)二階因子的乘積形式:
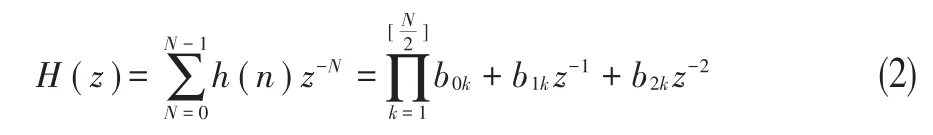
濾波器用二階節(jié)的級(jí)聯(lián)結(jié)構(gòu)來實(shí)現(xiàn),每個(gè)二階節(jié)采用橫截型結(jié)構(gòu),如圖2所示[6]:
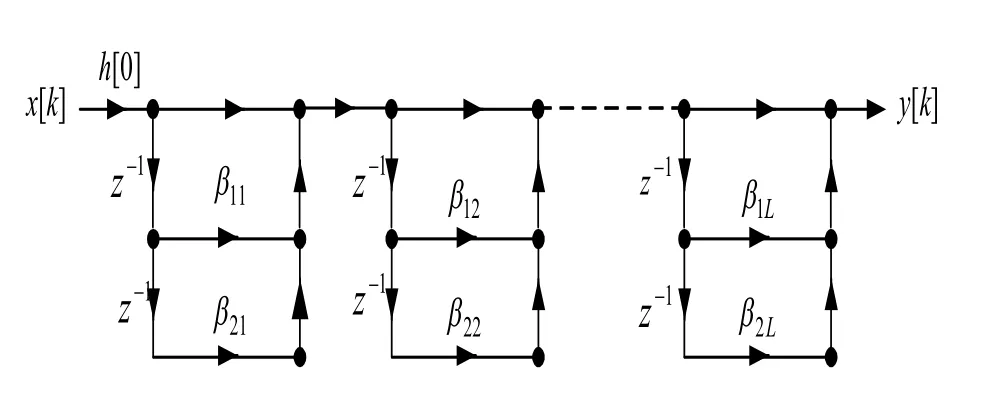
圖2 FIR濾波器級(jí)聯(lián)型結(jié)構(gòu)
(二)利用約束最小二乘法求濾波器系數(shù)方法。約束最小二乘法主要是采用最小二乘法與拉格朗日乘子法結(jié)合,即可以解決優(yōu)化問題,又能考慮帶約束的情況。
設(shè)一組超定矛盾方程為:

式中r≥e,rank(A)=e。最小二乘解為:χLS=(ATA)-1ATf
式中的解χLS只是所有r個(gè)方程的近似解,并不是精確解,如果需要精確滿足其中的rm個(gè)方程,就需要在某些頻率點(diǎn)上被精確控制,而剩下的點(diǎn),即余下的rs=r-rm個(gè)方程只要近似滿足就可以。所以,式(3)可以分解為rm個(gè)重要方程和rs個(gè)次要方程:

其中rm≤e和rs≥e。式(3)的約束最小二乘解χCLS的解:

使得Amχ=fm。為了求出拉格朗日乘子法求解式(3)描述的條件極值,首先建立拉格朗日函數(shù):
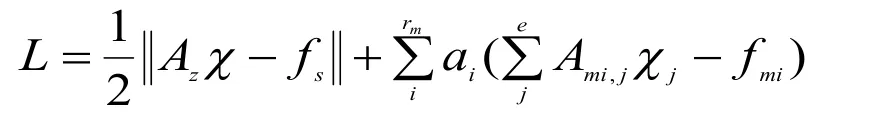
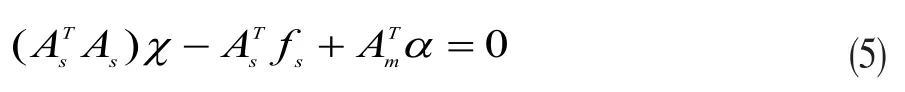
由上式知
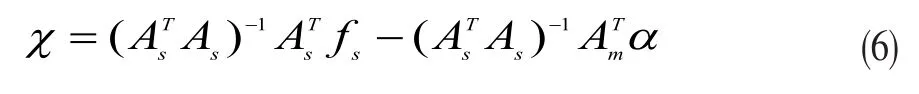
將式(5)代入約束條件(3),則得:
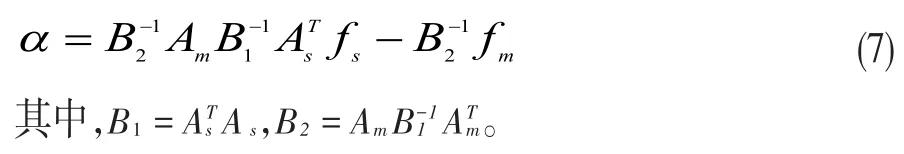
最后將式(7)代回式(5)就導(dǎo)出約束最小二乘法(CLS)的解為:
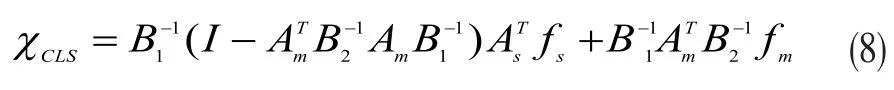
那么只要As和Am分別為列滿秩和行滿秩矩陣就存在,式(8)表達(dá)的約束最小二乘解也就存在。
為了確定FIR濾波器的階數(shù)N,在頻率[0,π]的取值范圍內(nèi),用H(ω)逼近Hd(ω),得到逼近曲線,也就是得先求出系數(shù)組:Φ(n)=[α(0,α(1),……α(r-1))]。
式(3)中的系數(shù)矩陣寫為:
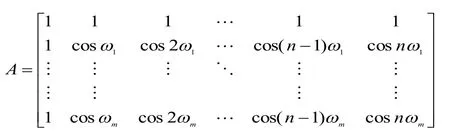
其中,ωi(i=1.2.…m)頻率在[ 0 ,π]的取值范圍內(nèi)分為稠密柵格,在某些需要特殊滿足的點(diǎn)上對(duì)幅值約束,例如在ω1=0或是過渡帶的一半處,得到方程,根據(jù)式(8)解出濾波器的系數(shù)Φ(n)。
三、FIR濾波器的仿真結(jié)果
(一)FI濾波器的仿真設(shè)計(jì)。利用MATLAB工具進(jìn)行仿真設(shè)計(jì),其幅度滿足下式:
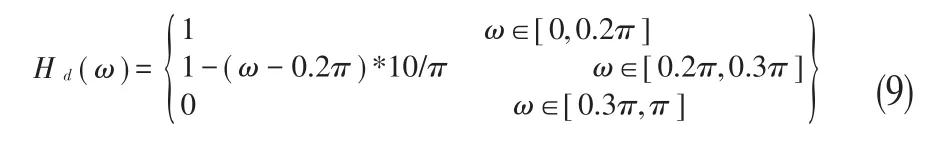
其中,截止頻率ωc=0.3π,要求H(0)=1,過渡帶的一半ω=0.25π處,H(ωc)=0.5。為設(shè)計(jì)出最優(yōu)的濾波器,需要:(1)濾波器階數(shù)N的選擇,以及N對(duì)濾波器性能的影響;(2)選擇精確方程的個(gè)數(shù),以及點(diǎn)的位置。
以階數(shù)N=12為例進(jìn)行了設(shè)計(jì),其中精確方程個(gè)數(shù)rm分別等于2、3、5即要求其中分別有2、3、5個(gè)重要方程被要求精確滿足,而其余rs=r-rm個(gè)次要方程近似滿足。
1、首先分別選擇的兩個(gè)點(diǎn)為ω=0,ω=0.25π,即
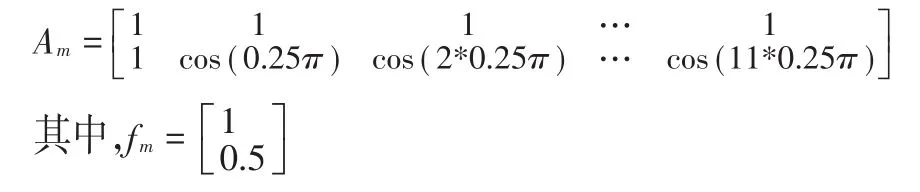
2、其次選擇三個(gè)重要方程的點(diǎn)分別是ω=0,w=0.25π,ω=0.3π,即
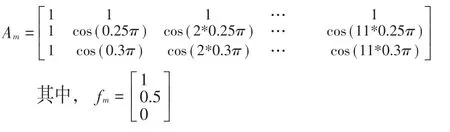
3、此外,再次分別選擇五個(gè)點(diǎn),ω=0,ω=0.2π,ω=0.25π,ω=0.3π,ω=0.35π,同時(shí)另選23個(gè)點(diǎn),作為次要方程點(diǎn)分別為,

即23個(gè)次要方程,其系數(shù)矩陣為:

(二)精確方程個(gè)數(shù)和濾波器階數(shù)對(duì)濾波器性能的影響
1.精確方程個(gè)數(shù)對(duì)濾波器性能影響分析。為了明確不同精確方程個(gè)數(shù)對(duì)濾波器性能的影響,分別設(shè)置精確方程個(gè)數(shù)的參數(shù)為rm=2,3,5進(jìn)行仿真模擬。
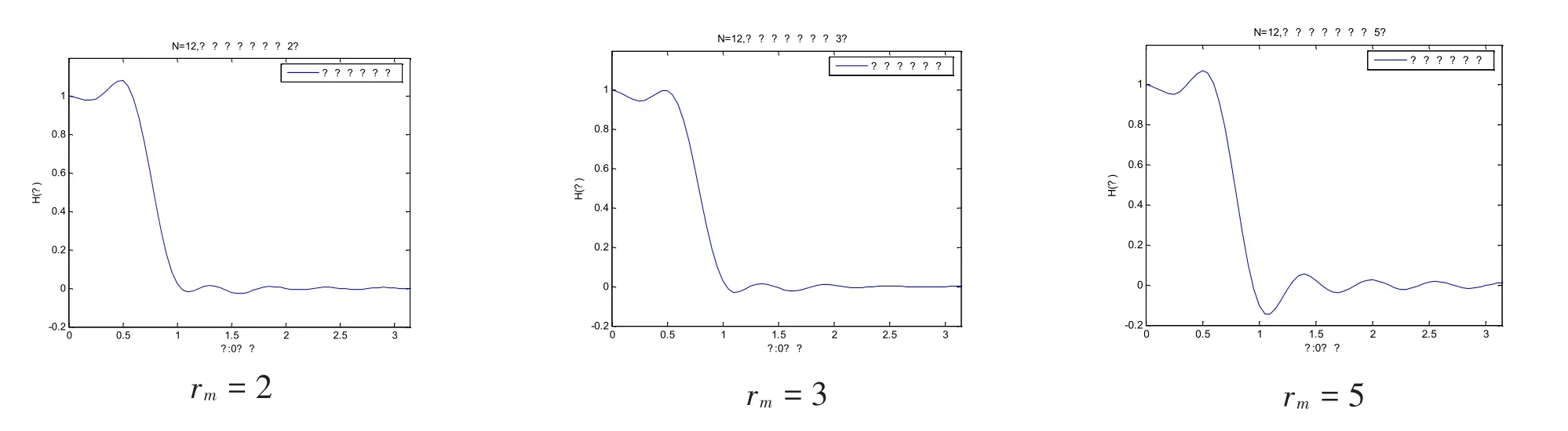
圖3 不同方程個(gè)數(shù)對(duì)濾波器性能的影響
從圖3可以看出當(dāng)rm=3時(shí),仿真出的濾波器和要求的濾波器的性能最接近。即當(dāng)精確方程的個(gè)數(shù)為3,且在點(diǎn)ω=0,ω=0.25π,ω=0.3π處對(duì)幅值約束,此時(shí)仿真得到的濾波器性能最好,最符合要求。
2.不同濾波器階數(shù)對(duì)濾波器性能的影響分析。對(duì)于濾波器階數(shù)N的選擇,經(jīng)過多次試驗(yàn),仿真結(jié)果如圖4所示:當(dāng)N=8時(shí),此時(shí)的濾波器阻帶最平穩(wěn);當(dāng)N=10時(shí),此時(shí)濾波器通帶最平穩(wěn),但是阻帶波動(dòng)較大;N=14時(shí),濾波器的通帶和阻帶都相對(duì)平穩(wěn).隨著N的增大,過渡帶也逐漸變窄。綜合上述結(jié)果,可以得到當(dāng)N=14時(shí)濾波器的性能最好,最符合要求.但無論N等于多少,仿真出的濾波器在約束的點(diǎn),即H(0)=1.00,H(ωc)=0.50,嚴(yán)格滿足設(shè)計(jì)要求。
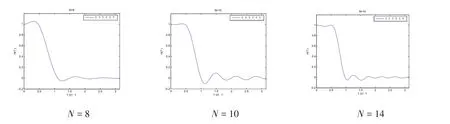
圖4 不同階數(shù)對(duì)濾波器性能的影響
(三)不同函數(shù)對(duì)濾波器性能的影響。然而考慮到在MATLAB進(jìn)行設(shè)計(jì)過程中,函數(shù)參數(shù)方法對(duì)于濾波器設(shè)計(jì)時(shí)振幅響應(yīng)有明顯的差異性。為了更好的了解約束最小二乘的優(yōu)缺點(diǎn),分別利用firls函數(shù)和remez函數(shù)設(shè)計(jì)相同參數(shù)的低通濾波器來進(jìn)行對(duì)比,其中濾波器階數(shù)N=14,rm=3,并運(yùn)行20次,濾波器參數(shù)如圖5所示。
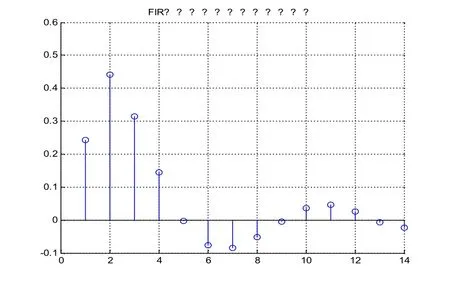
圖5 FIR濾波器系數(shù)分布圖
如圖6所示,與firls函數(shù)和remez函數(shù)相比約束最小二乘法執(zhí)行速度快且結(jié)果穩(wěn)定,在約束點(diǎn)可以被嚴(yán)格控制,更接近于理想約束點(diǎn)即H(0)=1.00,H(ωc)=0.50。同時(shí),在過渡帶上約束最小二乘法設(shè)計(jì)的濾波器相對(duì)較窄,設(shè)計(jì)通帶相對(duì)于其余兩種方法更平穩(wěn),但是阻帶有波紋,波紋相對(duì)不是很平穩(wěn),較比其余兩種方法幅度更大。
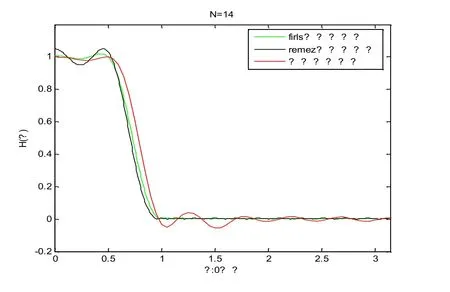
圖6 三種方法設(shè)計(jì)的濾波器的比較
綜上所述,運(yùn)用最小二乘法,結(jié)合拉格朗日法解決帶等式約束的FIR濾波器設(shè)計(jì),實(shí)驗(yàn)結(jié)果證明了其有效性。這種方法計(jì)算簡(jiǎn)便,易于實(shí)現(xiàn),具有通用性,可以根據(jù)需要通過調(diào)整參數(shù),設(shè)計(jì)所需的濾波器,具有較強(qiáng)的靈活性。
四、結(jié)論
本文介紹基于MATLAB的FIR數(shù)字濾波器設(shè)計(jì),使用最小二乘法處理所得的數(shù)據(jù),得到最優(yōu)擬合曲線,得到優(yōu)化曲線最小的階數(shù)與理想濾波器的關(guān)系曲線。主要得到以下結(jié)論:
(一)采用約束最小二乘法較firls函數(shù)和remez函數(shù)方法計(jì)算簡(jiǎn)便,易于實(shí)現(xiàn),更具有通用性。
(二)當(dāng)濾波器階數(shù)N=14,精確方程個(gè)數(shù)rm=3時(shí),濾波器性能最佳,通帶和阻帶都相對(duì)平穩(wěn)。
(三)約束最小二乘法在FIR濾波器設(shè)計(jì)中,對(duì)于濾波器幅頻響應(yīng)上更加接近理想約束點(diǎn)。
(四)采用MATLAB工具能夠很直觀地分析最小二乘法設(shè)計(jì)的優(yōu)缺點(diǎn)。

