考慮設備可用性約束的單機調度問題
王金鳳,陳 璐,楊雯慧
(上海交通大學 工業工程與管理系,上海 200240)
傳統調度方法假設設備總是可用的,但在實際生產過程中,許多因素會導致設備不可用,如更換刀具、設備檢修、設備突然故障等情況.當這些情況發生時,設備的不可用約束較容易量化,可以通過定義周期性不可用時段[1-2],或通過定義設備失效函數定義不可用約束[3].而當設備中的關鍵部件發生可靠性退化而影響工件的加工質量、加工速度或加工能耗時,設備同樣具有不可用性[4-5].因此,考慮設備狀態對可用性約束的影響對于生產調度具有重要的現實意義.然而,如何量化此類設備的可用性約束是一個很大的挑戰.在現有文獻中,沒有統一的方法來量化設備狀態對可用性的影響,應用最廣泛的是利用可靠性來衡量設備狀態,進而對設備的可用性進行量化[6-7].
在現有文獻中,設備不可用性通常分為單周期不可用、多周期不可用、柔性不可用3類,多數是以維護為代表的操作造成的設備不可用.Lee[8]作為開創者,首次在生產調度問題中考慮設備不可用,考慮單次已知開始時間和持續時間的不可用間隔.Kubzin等[9]在考慮設備單周期不可用時,假設其持續時間依賴于啟動時間,具有可控長度.但實際上,單周期不可用是對實際生產情況過分簡化的結果,與現實情況存在較大差異.Yu等[1]在此類問題中引入開始時間和持續時間都已知的多周期不可用間隔.蔣凱麗等[2]在模型中考慮具有時間窗的多周期不可用間隔.但由于影響間隔周期長短的因素較多,難以準確計算.當周期過短時會造成資源浪費,而周期過長又會導致設備失效率增加[10].Ahmadi等[11]引入基于狀態的不可用間隔,并通過對比實驗得出采用基于狀態的不可用間隔更具有現實應用意義的結論.Yildirim等[12]在研究中提出,當可靠性低于臨界閾值時,需引入單一級別的不可用間隔.Chen等[13]在此基礎上引入柔性不可用間隔,按照其效果分為3個級別:① 將設備恢復如新;② 改善部分設備狀態;③ 僅將設備恢復到失效前的工作狀態.但在上述研究中,設備失效并沒有被考慮在模型中.丁珮雯等[14]和Salmasnia等[3]在考慮設備狀態的單機調度問題研究中,也引入了柔性不可用.但以上研究均未考慮由可靠性過低而引發的設備不可用問題[15].
本文對單機調度問題進行了研究,同時考慮設備失效和設備可靠性對可用性的影響,選用不同類型的維護作業對設備狀態進行恢復,建立以最小化總拖期時間為優化目標的數學規劃模型,并設計開發了遺傳算法(GA)對問題進行求解,最后利用算例分析對算法的有效性及效率進行驗證.
1 設備可用性的定義
在可靠性、維修性術語中,將可用性定義為在要求的外部資源得到保證的前提下,設備在規定的條件下和規定的時間區間內處于可執行規定功能狀態的能力.利用設備可靠性對“可執行規定功能狀態的能力”進行量化.假設設備故障函數服從Weibull分布,可以表示為[16]
ρ(u)=λβuβ-1
(1)
式中:λ和β分別為Weibull分布的比例參數和形狀參數;u為設備役齡.當β>1時,該過程為非齊次泊松分布過程(NHPP),設備故障率隨時間的增長而逐漸增大.在此過程中,設備可靠性R可表示為
(2)
本文提出兩種等級的預防性維護策略:不完全維護 (IPM) 和完全維護 (PPM).IPM僅改善部分設備狀態,而PPM將設備狀態恢復如新.設備可靠性隨加工時間的演化過程如圖1所示.可靠性閾值δ作為衡量設備是否可用的標準,假設當設備可靠性介于[δ,1]時,設備可用;而介于[0,δ)時,設備不可用.由圖1可知,工件4和工件7的加工將導致設備可靠性超過臨界閾值,因此,必須在這兩個工件開始加工之前進行維護.此時,需要在維護時間和維護效果兩者之間進行權衡,確定維護級別(IPM或PPM),即選擇IPM所需維護時間較短,但可靠性改善程度有限,而選擇PPM可以使設備修復如新,但是所需維護時間較長.
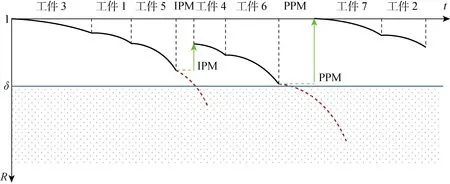
圖1 設備可靠性和可用性的關系Fig.1 Machine reliability versus availability
2 模型的建立
在考慮設備狀態的單機調度問題中,需要對工件集合N中的工件進行排序,目標是最小化總拖期時間.兩個相鄰工件中可以插入一次IPM或PPM以改善設備狀態.模型假設包括:① 在0時刻,所有工件均可加工;② 在加工前,設備役齡為0;③ 設備在同一位置只能加工一個工件,且一個工件只需加工一次;④ 忽略設備在加工不同工件之間的準備時間;⑤ 在加工過程中,設備發生故障修復后,被中斷的工件可以繼續加工,不需要額外的加工時間.
基于可靠性理論中的最優維護間隔(T*),設備可靠性的臨界閾值可表示為
(3)
基于NHPP假設,工位j上的累積故障次數可表示為
λ[(ufj)β-(ub1)β]
(4)
式中:ub1=0.
模型的決策變量為
由此建立數學模型如下:
(5)
s.t.
(6)
(7)
(8)
tPPMzj+tF(Mj-Mj-1)
(9)
?i∈N,?j∈N
ubj=uf(j-1)(1-θyj-zj),?j∈N
(10)
ufj≥ubj+xijpi,?j∈N
(11)
e-λ[(ufj)β-(ubj)β]≥δ,j∈N
(12)
yj+zj≤1,?j∈N
(13)
(14)
?i∈N,?j∈N
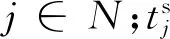

3 算法設計
考慮設備狀態的單機調度問題已被學者證明是NP難問題[17],引入計算可靠性的非線性約束(約束12),增加了求解難度.Lingo等商業求解器只能對有限規模的問題進行計算.因此,研究采用更為高效的遺傳算法進行求解,并通過C++語言實現.
3.1 編碼與解碼
染色體對工件加工序列進行編碼,圖1中算例的編碼染色體如圖2所示.

圖2 染色體編碼方式Fig.2 Chromosome coding
通過對染色體進行解碼,確定維護位置和維護方式,獲得一個完整的調度策略,其解碼算法如算法1所示.

算法1解碼
1.已知各工位j上的待加工工件的序號、加工時間以及δ.
2.根據式(2),計算工位j在完成工件加工后的設備可靠性R.
3.若R≥δ,則yj=zj=0,即表示不需要任何類型的維護.
4.否則,令yj=1,即假設在工位j上進行IPM,并計算該工位在完成工件加工后的設備可靠性R′.
5.若R′≥δ,則yj=1,zj=0,即在工位j上進行IPM.
6.否則,yj=0,zj=1,即在工位j上進行PPM.
7.j++,若j≤|N|,則返回步驟2;否則,繼續步驟8.
8.將各工位上的維護操作和工件序列結合,獲得完整的調度方案.
利用上述算法對圖2中的染色體編碼進行解碼,獲得一個完整調度方案,如圖3所示.

圖3 完整調度方案Fig.3 A complete schedule for sample problem
3.2 種群初始化
種群規模的大小會影響算法的性能及效率,所提算法中,種群規模Npop=50.首先,采用完全隨機的方式生成45個不同的個體作為初始解,繼而利用最早交貨期啟發式(EDD)規則生成5個較好的初始解,這樣既保證了初始種群的多樣性,同時能提高算法的收斂速度.
3.3 評價與選擇
3.4 交叉與變異
考慮到染色體代表個體的可行性,故對實數編碼的工序染色體采用兩點式交叉方法.交叉概率范圍一般為0.4~0.9.同樣,為保證染色體的可行性,對工序染色體采用換位變異方式.在變異過程中,引入Emmons規則[18]確定工件的優先關系,縮小搜索空間[19].
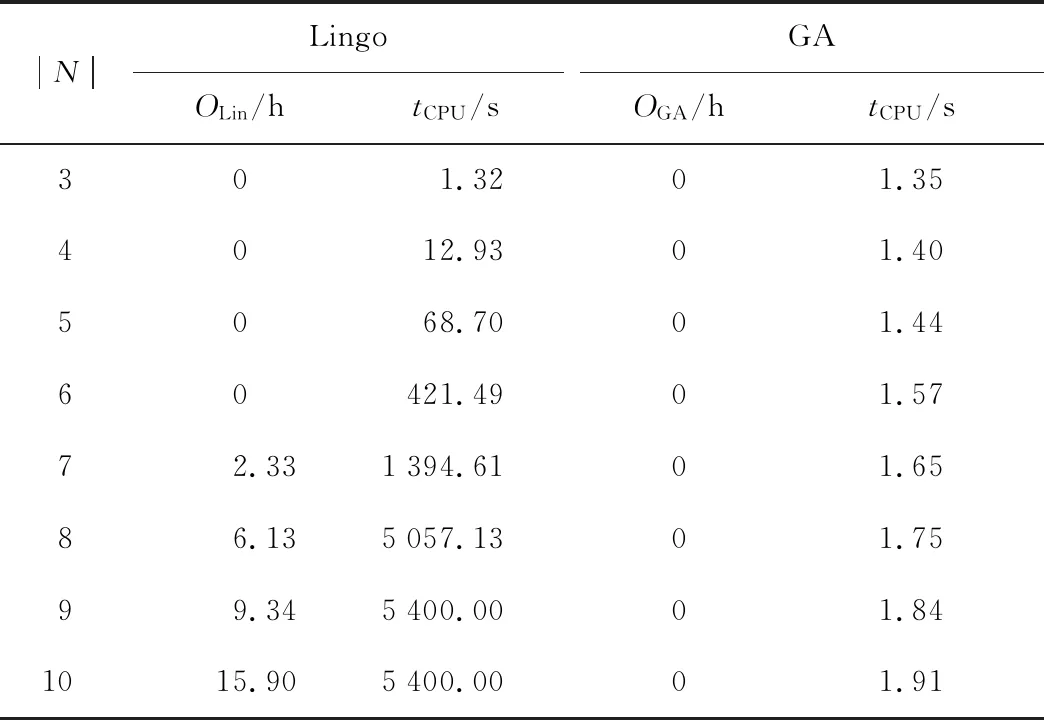
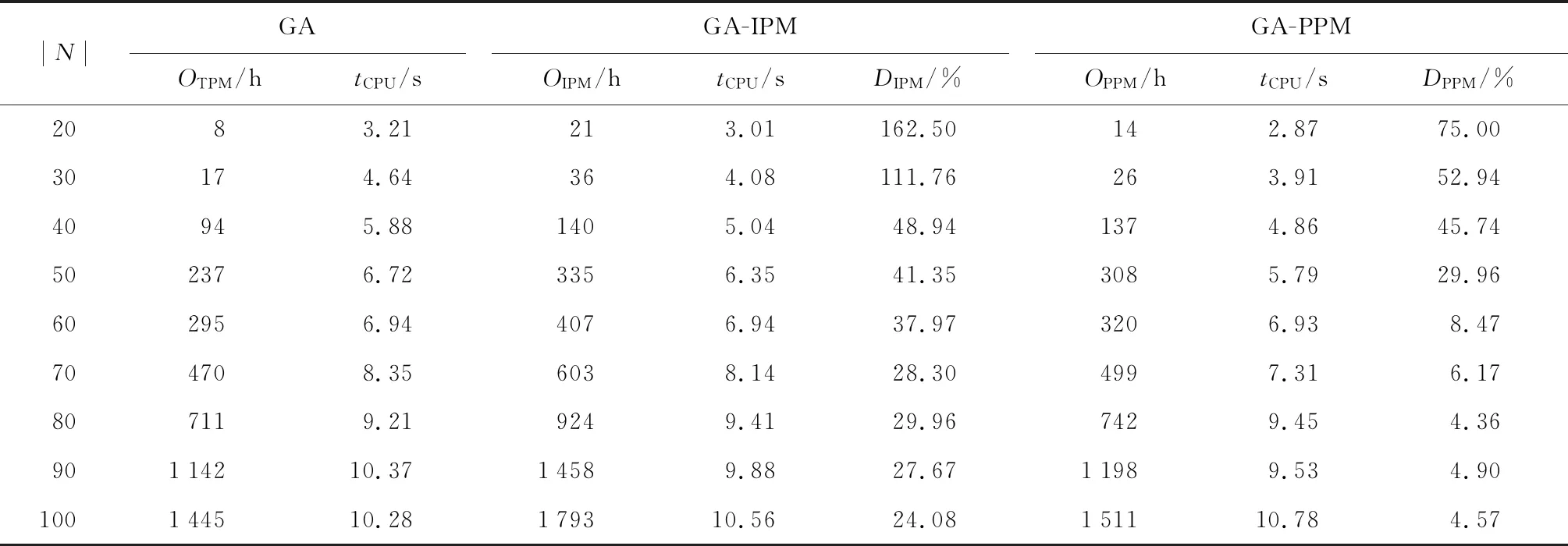
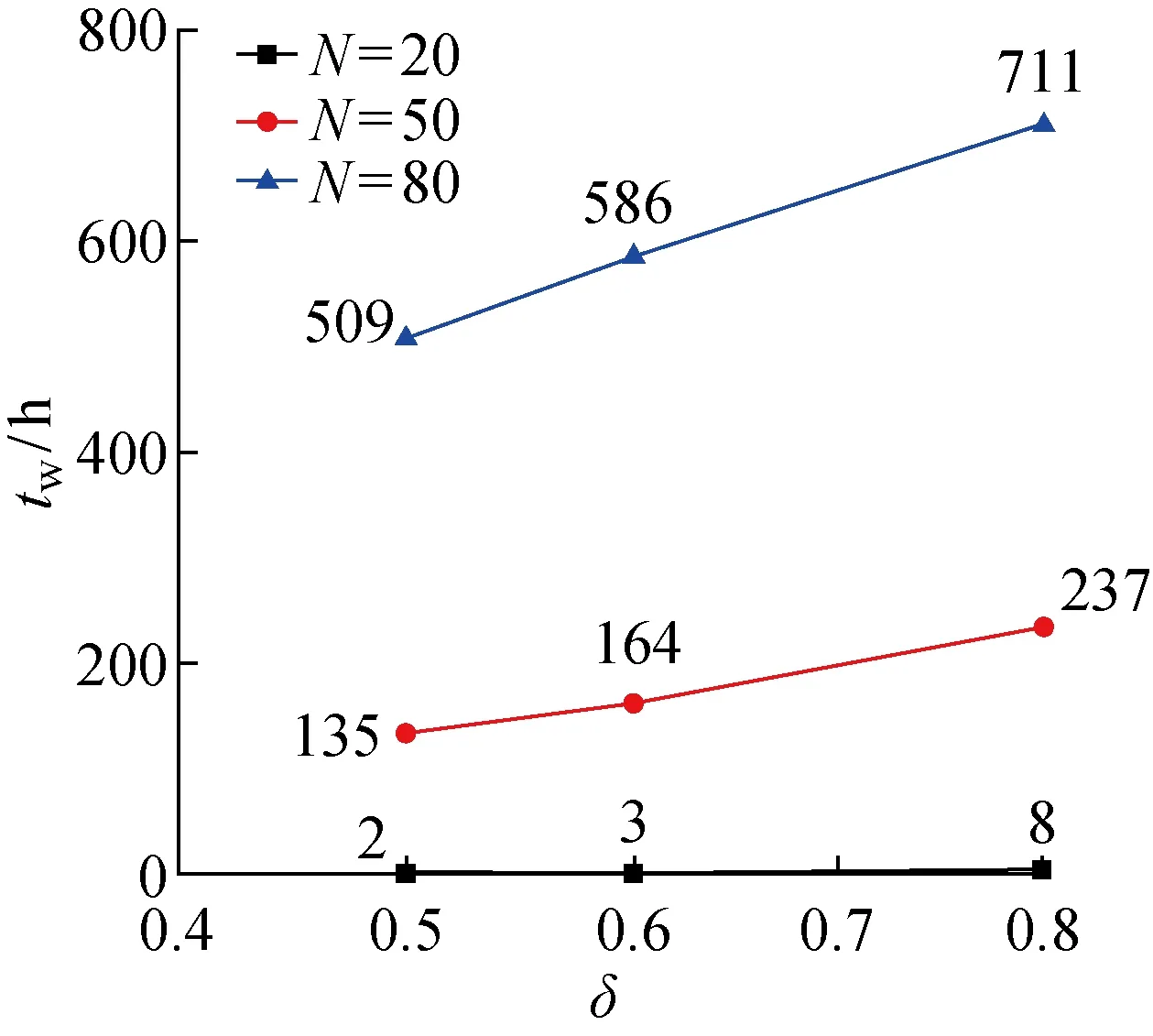
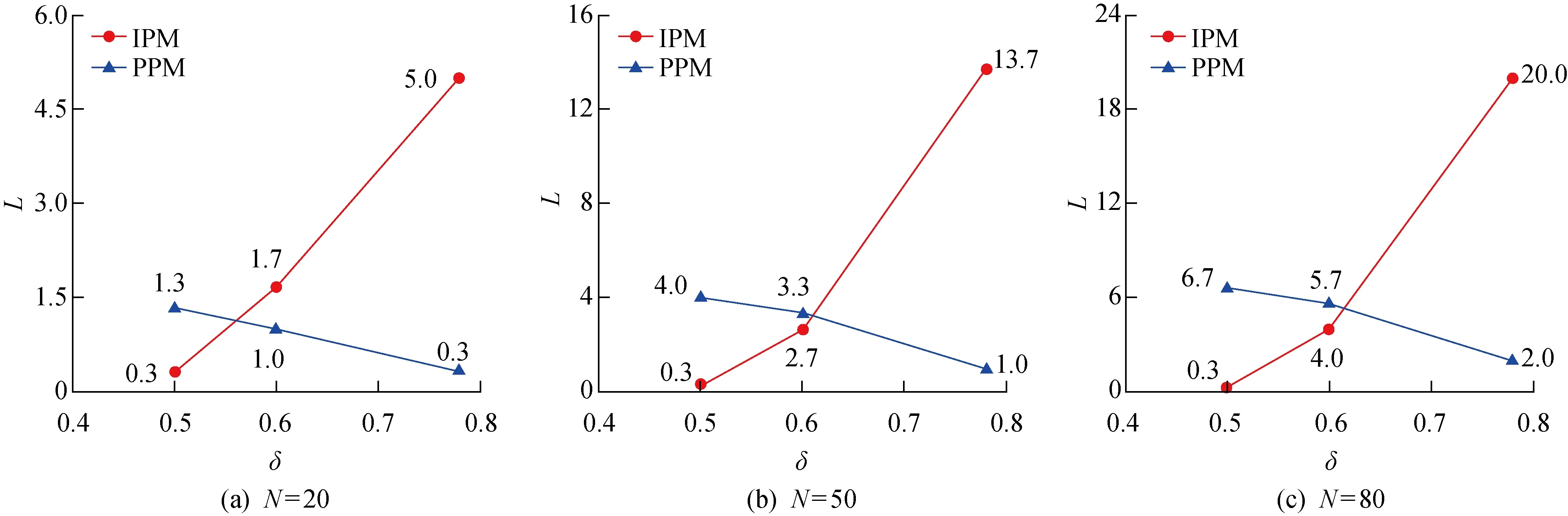
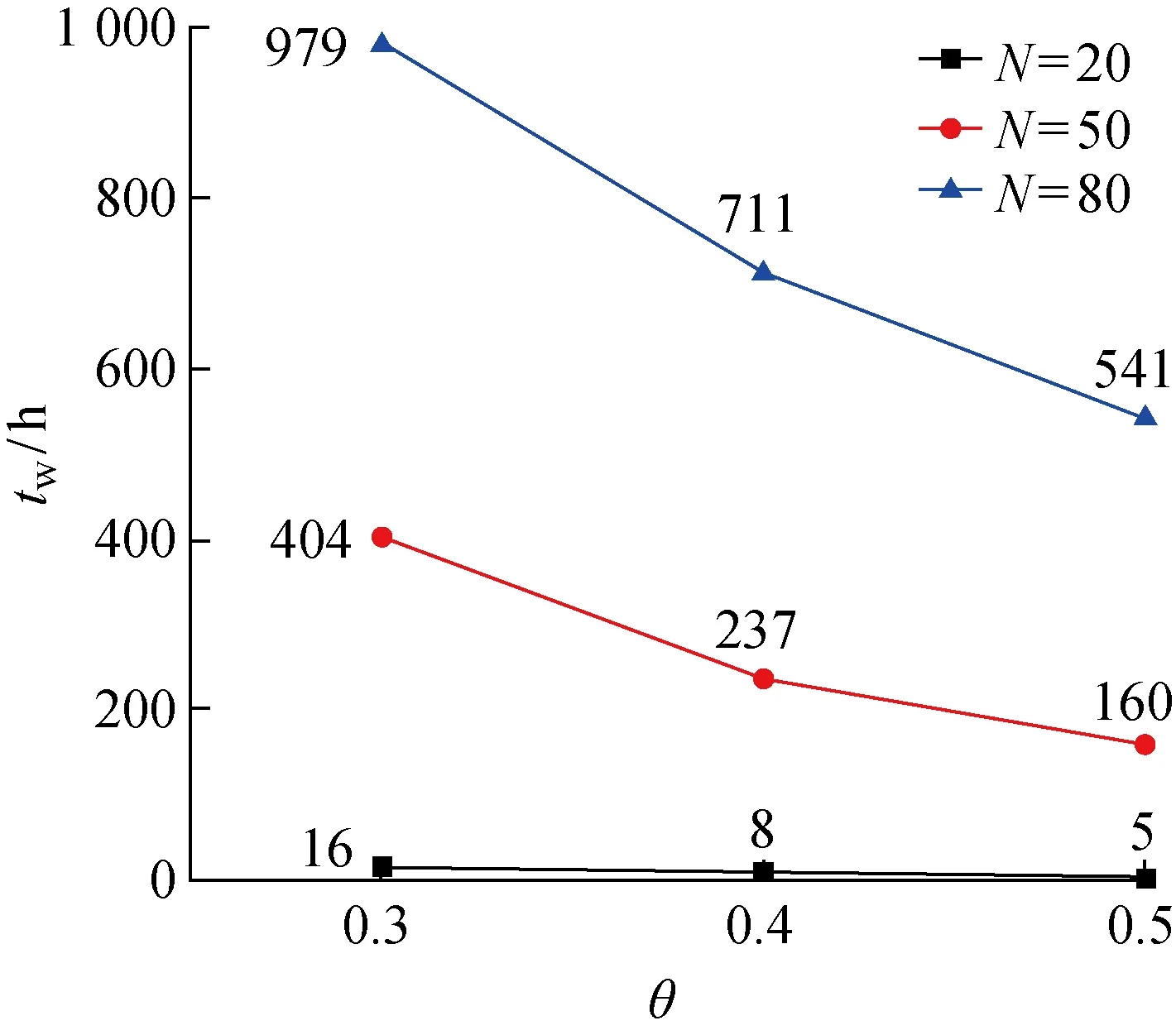
設Bi和Ai分別為在工件i加工前和加工后的工件集合,記為Bi→i和i→Ai.j 變異的發生需滿足上述優先規則,定義pm為變異概率.算法2詳細描述了變異過程. 算法2變異 1.已知各工位j上待加工工件的序號i、加工時間pi和交貨期di; 2.對于任意染色體,隨機生成(0,1)之間的數a; 3.若a>pm,則該染色體不進行變異,i++,返回2; 4.否則,隨機生成兩個滿足條件j 完整算法流程可見算法3. 算法3遺傳算法 1.已知算法參數Npop,Gmax,pc和pm. 2.初始化第1代種群,解碼后計算適應度值,得到最優個體π*和最差個體ω,并將π*的染色體序列復制給ω. 3.基于輪盤賭選擇法在種群中選取兩條染色體作為父代. 4.對父代進行交叉操作,得到子代. 5.對子代進行突變操作,得到新的子代. 6.對新的子代染色體解碼后,計算其適應度值,得到當前代最優個體π,最差個體ω,將 π的染色體序列復制給ω,并更新全局最優個體π*. 7.g++,若g≤Gmax,則返回3;否則,繼續8. 8.返回最優個體π*. 其中:g為當前代數;Gmax為最大迭代次數;pc為交叉概率;π*為最優個體;π為當前代最優個體;ω為當前代最差個體. 為證明遺傳算法的有效性,將遺傳算法所求的解與商業求解器Lingo所求的最優解進行比較.考慮8種不同規模的問題,分別在每種規模下生成10個算例.設置Lingo求解時限為 5 400 s.兩種解的比較如表1所示.其中,OLin和OGA分別為Lingo求解器和GA所求解的目標值;tCPU為運算時間. 由表1可知,在小于8個工件的算例中,GA不僅得到了最優解,而且在求解時間上明顯優于Lingo.當工件數量增加時,Lingo求解器無法在限定的時間內得到最優解,此時GA得到的最優解優于Lingo在規定時間內得到的最優解.因此,遺傳算法的有效性得以驗證. 表1 小規模算例實驗結果Tab.1 Results of small-scale instants 為了評估不同類型的維護作業對調度策略的影響,首先對GA進行修改,得到以下兩種算法: (1) GA-IPM:對任意一個工位j,令zj=0,此時算法只考慮IPM. (2) GA-PPM:對任意一個工位j,令yj=0,此時算法只考慮PPM. 將第3節中提出的GA所求的解作為基準解,分別計算GA-IPM和GA-PPM所求解的偏差: (15) (16) 式中:OTPM,OIPM和OPPM分別為GA、GA-IPM和GA-PPM所求解的目標值,其結果如表2所示. 表2 不同GA在中、大規模算例中的表現Tab.2 Performance of different GAs on medium and large scales 由表2可知,同時考慮兩種維護作業對減少總拖期時間具有一定的優越性,這種優越性隨問題規模的增大而減小,最終趨于穩定,相比于GA-IPM和GA-PPM的改善分別維持在25%和5%左右.另外,與GA-IPM相比,GA-PPM表現更優.由此可見,雖然PPM耗時長,但能更顯著降低設備的失效風險,從而達到縮短總拖期時間的效果. 下文將分別針對可靠性閾值和設備狀態改善因子進行敏感性分析. 4.3.1可靠性閾值對調度決策的影響 考慮3個級別的可靠性閾值,分別為δ=0.5,δ=0.6,δ=0.78.其中,δ=0.78是通過式(3)計算出來的臨界閾值.在其他參數設置保持不變的情況下,對比不同可靠性閾值對調度決策的影響,如圖4和5所示.其中:tW為總拖期時間;L為維護次數. 由圖4可知,隨著可靠性閾值的增加,總拖期時間增大.問題規模越大,這種變化趨勢變得更加明顯.造成這種現象的原因為,隨著可靠性閾值的增加,設備需要更頻繁的維護作業,使得設備可靠性能夠保持在閾值之上.而當維護作業時間增加時,總拖期時間也增加.然而,當設備可靠性閾值降低時,設備在加工時的狀態較差,將會導致加工工件的質量降低. 圖4 不同可靠性閾值下的總拖期時間Fig.4 Total tardiness at different reliability thresholds 由圖5可知,當可靠性閾值增加時,采用IPM的次數增加,采用PPM的次數減少.原因是IPM能夠以較短的耗時將設備可靠性恢復到閾值之上,而PPM則在恢復效率(改善效果與維護時長的比值)上稍顯劣勢.由此可見,在可靠性閾值增加時,調度決策更加側重維護的效率. 圖5 不同可靠性閾值下的維護次數Fig.5 Times of maintenance at different reliability thresholds 4.3.2狀態改善因子對調度決策的影響 考慮3種不同程度的狀態改善因子,分別是θ=0.3,θ=0.4,和θ=0.5.在其他參數設置保持不變的情況下,對比不同狀態改善因子對調度決策的影響,如圖6和7所示. 由圖6可知,當改善因子增加時,總拖期時間相應降低,這種變化趨勢隨著問題規模的增大而變得更加明顯.這是由于在IPM耗時不變的前提下,隨著改善因子的增加,IPM的效率提高,節省了維護時間,從而減少了總拖期時間. 圖6 不同改善因子下總拖期時間的變化曲線Fig.6 Total tardiness with different improvement factors 由圖7可知,當改善因子增加時,采用IPM的次數增加,PPM的次數減少至0. 圖7 不同改善因子下的維護次數Fig.7 Times of maintenance with different improvement factors 以上結果表明,在實際生產調度決策時,可以通過提高維護效率,提高可靠性改善效果來降低生產交付的壓力. 本文研究了某轉子車間內單臺設備的生產調度問題,考慮設備可用性約束,以及不同級別的維護作業,優化目標為最小化總拖期時間.優化模型中通過可靠性來表征設備的可用性約束,減少當設備可靠性下降時對加工質量的影響.設計開發了遺傳算法對模型進行優化求解.實驗結果表明,所提方法能夠有效量化設備可用性對生產調度的影響,并能夠合理地選擇不同類型的維護作業,以減少總拖期時間.靈敏度分析為車間內實際生產調度提供決策支持,具有實際應用價值.后續研究將把該方法應用于更復雜的生產環境中,如并行機、流水線生產等.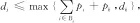
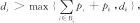

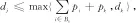
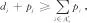
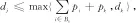
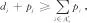
3.5 算法流程

4 算例驗證與分析
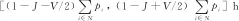
4.1 小規模算例驗證
4.2 中、大規模算例驗證
4.3 敏感性分析

5 結語

