高速鐵路列車運行速度提高對車體加速度的影響分析

楊 飛,趙文博,孫加林,龍亦語

(中國鐵道科學研究院集團有限公司基礎設施檢測研究所,北京 100081)

建設更高速度等級的高速鐵路及提高既有線路的運行速度是當今世界鐵路發展的主流趨勢。隨著列車運行速度的提高，列車與軌道之間的相互作用將會更加顯著，線路狀態對軌道系統及車輛系統的影響更加明顯[1-2]。

馮青松[3]研究列車速度對軌道振動的影響，得出隨著速度的提高，動態輪軌力及最大鋼軌、軌枕和道床振動加速度不斷增大。左玉良[4]通過對同一線路不同檢測速度得到的檢測數據進行對比，得出不同速度下軌道幾何波形相近，僅幅值有一定的差異。趙國堂[5]指出輪軌垂向力、輪重減載率等隨著列車速度的提高明顯增大。羅林[6]研究車體加速度與軌道不平順波長的關系時，簡單認為普速列車車體加速度近似是軌道不平順的二階導數。日本根據多年運行經驗推斷出列車搖晃加速度正比于列車速度，但是我國和日本兩國在車輛類型、線路條件、軌道不平順特征等方面存在著差別，不能完全直接照搬照用[7]。總體而言，目前研究局限于列車運行速度對高速鐵路系統動力響應影響的定性分析階段，對于列車運行速度與車體振動影響之間的定量關系國內并未見相關研究。

近年來，既有高速鐵路已大面積地恢復到設計速度運營，甚至將來有可能會提高到更高速度運行。根據高鐵線路聯調聯試以及日常檢測數據顯示，目前既有高速鐵路安全性冗余空間較大，提速面臨的最主要問題是乘車舒適性得到保持[8]。因此有必要開展高速列車車體振動加速度與運行速度之間的關聯性分析，以便掌握在相同線路工況下隨著運行速度的提高，車體振動響應等指標的舒適性余量范圍。

綜上所述，為了準確掌握高速鐵路恢復設計速度或既有線路提速等對運行舒適性的影響規律，通過對大量實車試驗數據的統計及回歸分析[9]，同時結合車輛動力學仿真計算結果，研究運行速度與車體振動加速度等舒適性指標之間的關聯性規律，定量地給出了車體振動加速度與運營速度之間的關聯性數學模型，為將來既有鐵路提速提供理論支撐。

1 數據采集及處理

為了研究列車運行速度提高與車體加速度的關系，需要采集相同區段不同行車速度時車體加速度數據，因此宜選用線路開通前動態驗收逐級提速期間的實測數據[10]。軌道高低不平順主要影響車體垂向振動，軌向不平順主要影響車體橫向振動[11]，由于車體橫向振動除受到軌向不平順影響外，在曲線、緩和曲線區段還受到預設超高的影響，因此不能直接分析橫向加速度與運行速度的關系，后續主要針對車體垂向振動進行分析。

本文選擇設計時速350 km的8條高速鐵路作為研究對象，各線路選取里程區段及對應的綜合檢測列車車型見表1。分別對速度等級200，250，300，350 km/h的檢測數據進行統計分析。由于高速鐵路平順性較好，車體振動加速度普遍較小，因此測點多選用引起較大車體振動加速度的長波不平順區段。此外綜合檢測車按照某一時速進行檢測時，在線路兩端有加/減速過程，分析時將剔除未達到計劃檢測速度級的區段。

表1 實測數據測點

選取實測數據共計413組，分析得出以上區段不同檢測速度與車體振動加速度的對應關系，如圖1所示。其中200 km/h檢測速度所對應的車體加速度集中在(0.02～0.043)g，250 km/h檢測速度所對應的車體加速度集中在(0.022～0.061)g，300 km/h檢測速度所對應的車體加速度集中在(0.026～0.082)g，350 km/h檢測速度所對應的車體加速度集中在(0.028～0.10)g，g為重力加速度，9.81 m/s2。

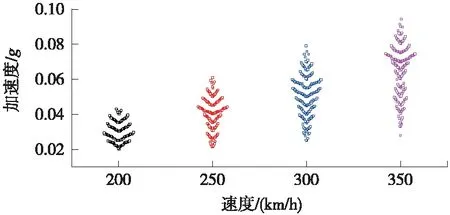
圖1 不同速度檢測下車體振動加速度分布

2 實測數據分析

由圖1可以看出：隨著運行速度的提高，車體振動加速度有整體增大趨勢。為了定量地得到車體振動加速度與運行速度的關聯關系，需要從車輛系統多體振動原理進行定量分析。

以余弦型軌道不平順激勵為例[12]，軌道不平順形式為

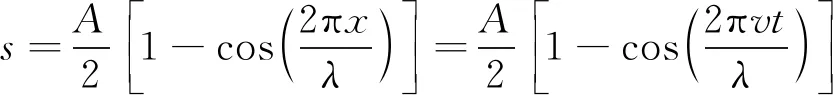
(1)

式中，s為軌道不平順幅值，mm，同時也為輪對位移；A為軌道不平順峰值，mm；x為到起點的距離，m；λ為不平順波長，m；v為速度，m/s；t為時間，s。

由微積分及動力學[13]知識可知，加速度為位移的二階導數，因此可以得出加速度計算公式為

(2)

式中，amax為加速度最大值，m/s2。

可以看出，理想無阻尼自由振動條件下的車體振動加速度與列車運行速度關系如下

(3)

式中，v1為提速前列車運行速度；v2為提速后列車運行速度，m/s；a1為提速前列車車體振動加速度；a2為提速后列車車體振動加速度，m/s2。

式(3)表明：理想無阻尼自由振動條件下，車體加速度比與運行速度比的平方呈正比，然而實際列車運行中由于懸掛系統的阻尼耗散會衰減車體振動[14]，因此公式(3)需要根據實際的高速列車振動加速度與速度關系進行修正。

根據收集到的4個運行速度級檢測數據，得到6個運行速度比及相應的車體加速度比，加速度比箱線圖按照速度比大小排列如圖2所示。由圖2中的加速度比下四分位數、中位數、上四分位數、平均數及最值可以看出：運行速度比越大，車體加速度比也越大；同一速度比下，加速度中位數與均值近似，且除350/200 km/h運行速度比下加速度離散性偏大外，其他速度比下加速度比離散性較小，一半以上區段的加速度比集中在均值左右0.3數值范圍以內，具體見表2所示。

圖2 不同速度比下加速度比箱線圖

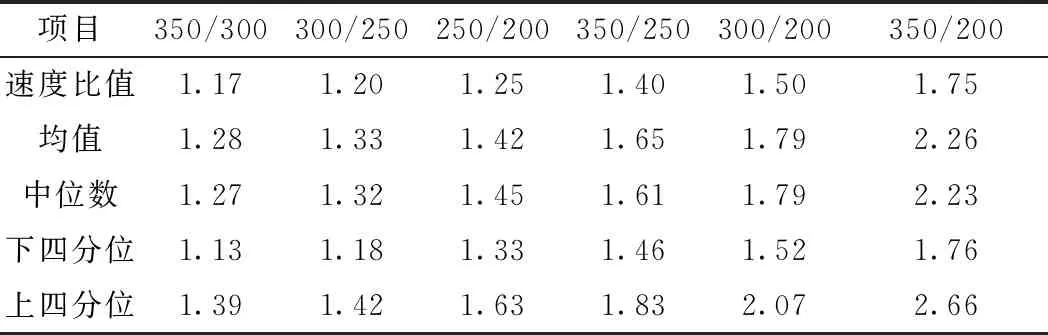
表2 不同速度比下加速度比統計結果

以加速度均值為參考，可以得出加速度比與速度比的大致對應關系，根據式(3)加速度比與速度比呈冪函數形式，因此對不同速度比下加速度比進行冪函數擬合，數值擬合結果如圖3所示。擬合誤差為0.02，得出擬合公式為

y=x1.46

(4)

式中，y為車體加速度比；x為運行速度比。

圖3 加速度比均值與速度比關系

3 動力學仿真模型

3.1 模型介紹

采用UM多體動力學仿真軟件[15]建立典型高速動車組車輛動力學模型，車輛包含車體、構架、軸箱、輪對等共15個剛體，其中除軸箱只有繞輪軸的1個轉動自由度外，其余剛體均有6個自由度，分別是縱移、橫移、沉浮、側滾、點頭、搖頭，總計50個自由度，車輛動力學模型如圖4所示，建模中所用的部分動力學參數見表3。

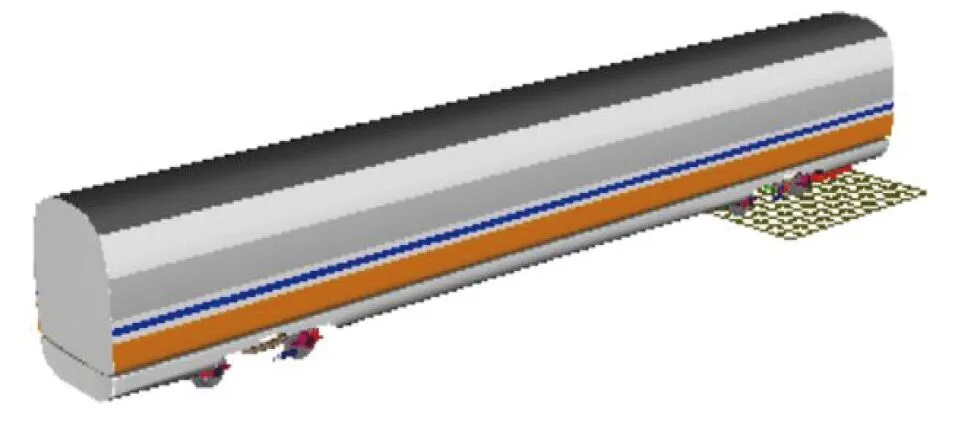
圖4 高速車輛動力學模型

表3 CRH2型列車部分參數

3.2 模型驗證

為了驗證所建立的動力學模型有效性，結合綜合檢測列車[16]在現場得到的檢測數據，與仿真結果進行對比分析。仿真中輸入的軌道不平順為綜合檢測列車實測的高低和軌向不平順，動力學仿真模型車輛運行速度與實際檢測中速度保持一致，得到仿真結果中車體垂向加速度和實車檢測得到的垂向加速度，如圖5所示。可以看出列車垂向加速度仿真結果與實測結果波形重復性較好。

圖5 仿真結果與實測結果對比

利用平均絕對誤差MAE[17]、均方根誤差RMSE[18]、希爾不等系數TIC與相關系數ρ[19]等指標定量評價仿真模型計算結果的可靠性，各指標計算方法如下

(5)

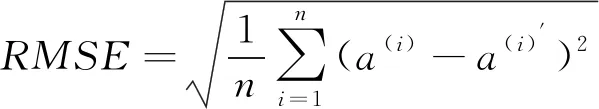
(6)

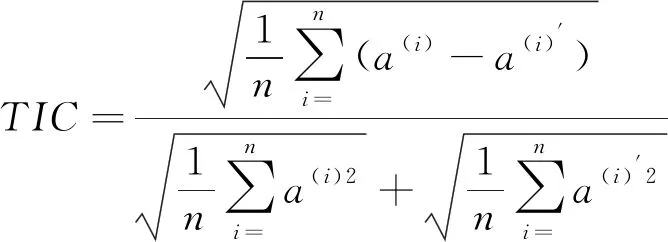
(7)

(8)

式中：a(i)和a(i)′分別為實測加速度數據a和仿真加速度數據a′的第i個值，i=1，2，…，n，n為測試數據容量；Cov(·)為協方差，Var(·)為方差。

MAE和RMSE反映了預測的絕對準確度；TIC和ρ為相對準確度指標，TIC介于0和1之間，越接近0預測準確度越高；ρ介于-1和1之間，越接近1預測準確度越高，具體結果如表4所示。結果表明：仿真計算的誤差范圍完全可以滿足實際工程的需要，充分驗證了仿真模型的準確性。

表4 準確度指標統計

4 仿真計算及結果分析

4.1 諧波軌道不平順工況

由于軌道不平順包含著不同的波長成分，其中中短波不平順主要影響輪軌安全性指標，長波不平順則主要影響車體振動加速度等舒適性指標[20]。仿真分析不同波長范圍軌道不平順作用下，列車運行速度與車體振動加速度的關聯關系，軌道不平順采用公式(1)描述的余弦波形式，如圖6所示。

圖6 余弦型不平順

軌道不平順波長選用對車體加速度影響較大的40～120 m波長，以5 m為步長，幅值選用15 mm，得到不同速度條件下的車體加速度與軌道不平順波長關聯關系，結果如圖7所示。

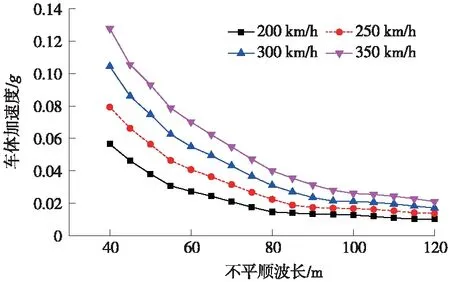
圖7 不同波長軌道不平順激勵，車體加速度與運行速度的關系

同樣，統計4個速度等級數據，得出了6個速度比及加速度比的關系如圖8所示。結果表明，相同速度比下加速度比離散性較小，50%以上區段的加速度比集中在均值左右0.3范圍以內，具體數值見表5。

圖8 不同運行速度比下車體加速度比箱線圖

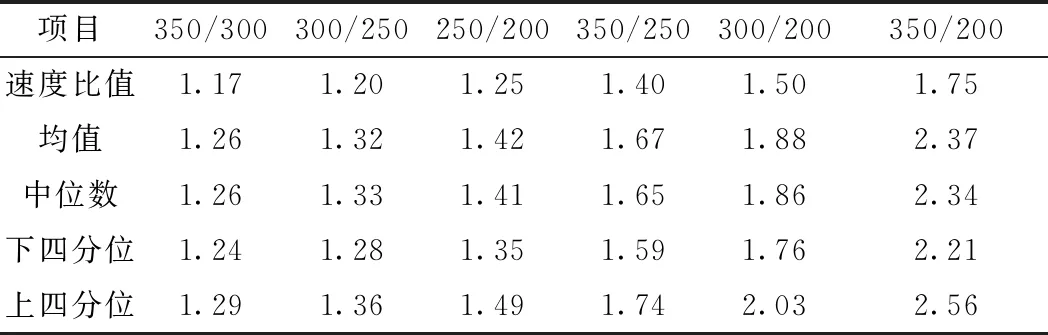
表5 不同運行速度比下車體加速度統計

以加速度均值為參考，得出加速度比與速度比的大致對應關系，對不同速度比下加速度比進行冪函數擬合，結果如圖9所示。擬合誤差為0.009，得出公式為

y=x1.54

(9)

圖9 車體加速度比均值與運行速度比關系

4.2 隨機軌道不平順工況

實際線路軌道不平順為隨機不平順，然而實測數據只有一種速度等級，因此為研究隨機不平順激勵下車體加速度與速度的關系，需要以實測軌道隨機不平順為輸入進行仿真計算，輸入的實測軌道不平順形式如圖10所示。

圖10 實測軌道隨機不平順

列車加速度不僅與速度有關，還與軌道不平順波長、幅值和形式等相關，因此需要選用多組數據進行統計分析。本文選取實測軌道不平順區段100處，作為激勵，分別計算不同運行速度時的車體加速度響應，得到不同速度比下加速度比如圖11所示，具體數值見表6。

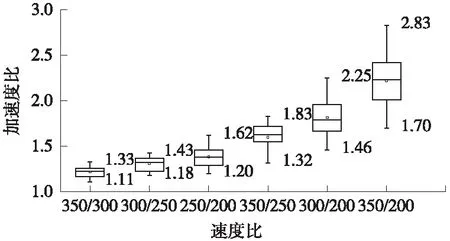
圖11 不同運行速度比下車體加速度比箱線圖

表6 不同運行速度比下車體加速度統計

同樣以加速度均值為參考，得出車體加速度比與運行速度比的大致對應關系，對不同速度比下加速度比進行冪函數擬合，結果如圖12所示。擬合誤差為0.02，得出擬合公式為

y=x1.43

(10)

圖12 車體加速度比均值與運行速度比關系

5 結論

通過大量實測數據統計分析及動力學仿真計算，研究既有高鐵線路速度提升對乘坐舒適性的影響規律，提出車輛運營速度與車體振動加速度之間的定量關聯關系。研究結論如下。

(1)結合高速鐵路聯調聯試逐級提速實測數據，統計分析得出車體振動加速度比與運行速度比呈冪函數關系，且擬合得出加速度比與速度比的1.46次方呈正比。

(2)諧波不平順動力仿真結果表明，加速度比與速度比的1.54次方呈正比；隨機不平順動力仿真結果表明，加速度比與速度比的1.43次方呈正比。

(3)根據綜合實測數據和動力學仿真分析結果，提出車體振動加速度比與運行速度比的1.5次方近似呈正比。研究成果可以為鐵路提速滿足舒適性、軌道狀態間接評判以及現場養護維修工作提供理論指導。