數學模型在傳染病建模中的應用

上海健康醫學院 醫療器械學院 上海 213038

數學建模對于激發大學生的學習興趣、增強數學創新實踐能力、提升競爭意識和創新意愿等方面的積極作用已經成為教育界的共識[1]。然而,學生們在遇到實際問題時常常感到無從下手,課堂上學到的相關知識不能進行有效的轉化和應用。如何學以致用,提高解決實際問題的能力一直是學者們關注的問題。在傳染病建模中,長期占據主導地位的是倉室模型,這一思想是由Robert和May提出的,目前仍在不斷的沿用和發展,所謂的倉室模型是指針對某類傳染病的傳播特點把人群分為相應的類群,然后根據疾病的傳播規律,構建相應的數學模型[2]。本文將采用倉室模型的基本思想,著重介紹四類常見傳染病的建模思路。

1 艾滋病傳播模型(SI模型)

因此,該疾病的數學模型可以表示為:

2 流感模型(SIS)

SIS模型與SI模型的主要差異在于SIS模型中被感染者可以被治愈,比如季節性流感等。但是由于流感病毒容易變異,所以痊愈的病人仍然有被感染的可能性,因此該模型需要在SI模型的基礎上考慮病愈后的個體重新回到易感者人群中,也即需要用SIS模型來描述。假設病人從感染者轉變為易感者的概率為α,其他參數和上面相同,我們可以用以下常微分方程組來描述該模型:

3 急性傳染病模型(SIR)及其拓展模型(SIRS)

SIR模型刻畫的傳染病為發病迅遠,康復后體內含有終身免疫的抗體,不會再被感染的疾病,如:天花、麻疹、腮腺炎等。由于痊愈后個體具有免疫力,不會被再次感染,所以對于這類疾病而言,應將人群劃分為易感者(S)、感染者(I)和移出者(R)三類,γ,則單位時間會有γI個感染者進入移出者倉室,模型的具體形式如下:

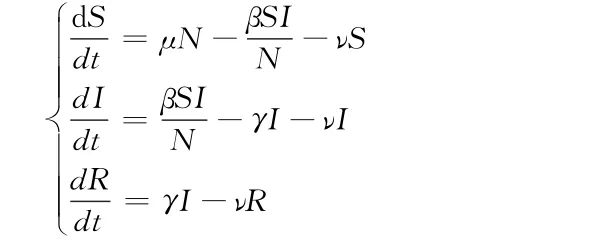
SIRS模型與SIR模型的區別在于,后者具有終身免疫期,康復的病人不會再次被感染;而前者有暫時的免疫期,病人康復后先進入移出者倉室,然后再以一定的比例進入易感者倉室。

4 帶潛伏期的傳染病模型(SEIR)

SEIR模型刻畫的是具有感染潛伏期,在潛伏期內不表現出感染癥狀,但是能夠感染易感者個體,并且治療康復后將產生抗體不會再被感染的疾病,如SARS疾病,所以對于這類疾病而言,應將人群劃分為易感者(S)、潛伏者(E)、感染者(I)和移出者(R)四類,假設潛伏者確診感染的概率為σ,疾病的康復率為γ,其他參數與前面相同,那么模型的具體形式如下:

綜上,本文只是從疾病傳播機理的角度介紹了四類傳染病最基本的數學建模方法,而在實際問題中疾病的傳播是非常復雜的過程,例如疾病的垂直傳染性、時滯因素和參數的確定等,需要我們綜合考慮各種因素,制定出最能反映實際情況的模型,只有這樣才能真正做到理論聯系實際。