研究生入學考試《高等數學II》積分知識統計分析

保山學院 數學學院 云南 保山 678000

1 引言

《高等數學》是教育部指定的理工科專業、經濟類、管理類及農林類等相關專業學專業核心課程之一,也是專業后繼課程的學習的理論基礎。如物理學,水利水電工程、信息與計算科學、網絡工程、通信工程、土木工程等相關專業的基礎課程,大學生只有掌握好高等數學的知識后,才能比較順利地學習其他的專業課程[1-3]。《高等數學》是學生必須掌握但又比較難掌握的專業基礎課程之一,它的數學思想、數學思維、數學方法、基本理論知識不僅是理工科、經濟類、管理類及農林類等相關專業后繼課程的學習的必要工具和理論基礎,也是考研數學中涉及內容最多,占比例最大,考點最靈活的一門課程[2-5]。因此,理工科、經濟類、管理類及農林類等相關專業的大學生必須學好《高等數學》這門課程,為以后的升學、學習、工作打下良好的基礎。本文從2005—2019年考研高等數學II入手,對考研《高等數學II》中積分知識的題型、分值、主要考點進行統計,結合多年《高等數學》考研指導經驗,提出相關復習建議。

2 研究生入學考試《高等數學II》中積分知識的題型、分值、知識點分布情況

2.1 關于積分的題型、分值分布情況 對2005-2019考研《高等數學II》中有關積分知識的題型、分值進行統計見表2-1,得出有關積分知識主要考核的題型是選擇題、填空題和計算題、分值主要在32分到56分之間,其中2015年的分值為32分,2010年的分值為56分,其他幾年的分值在39—50分之間波動。

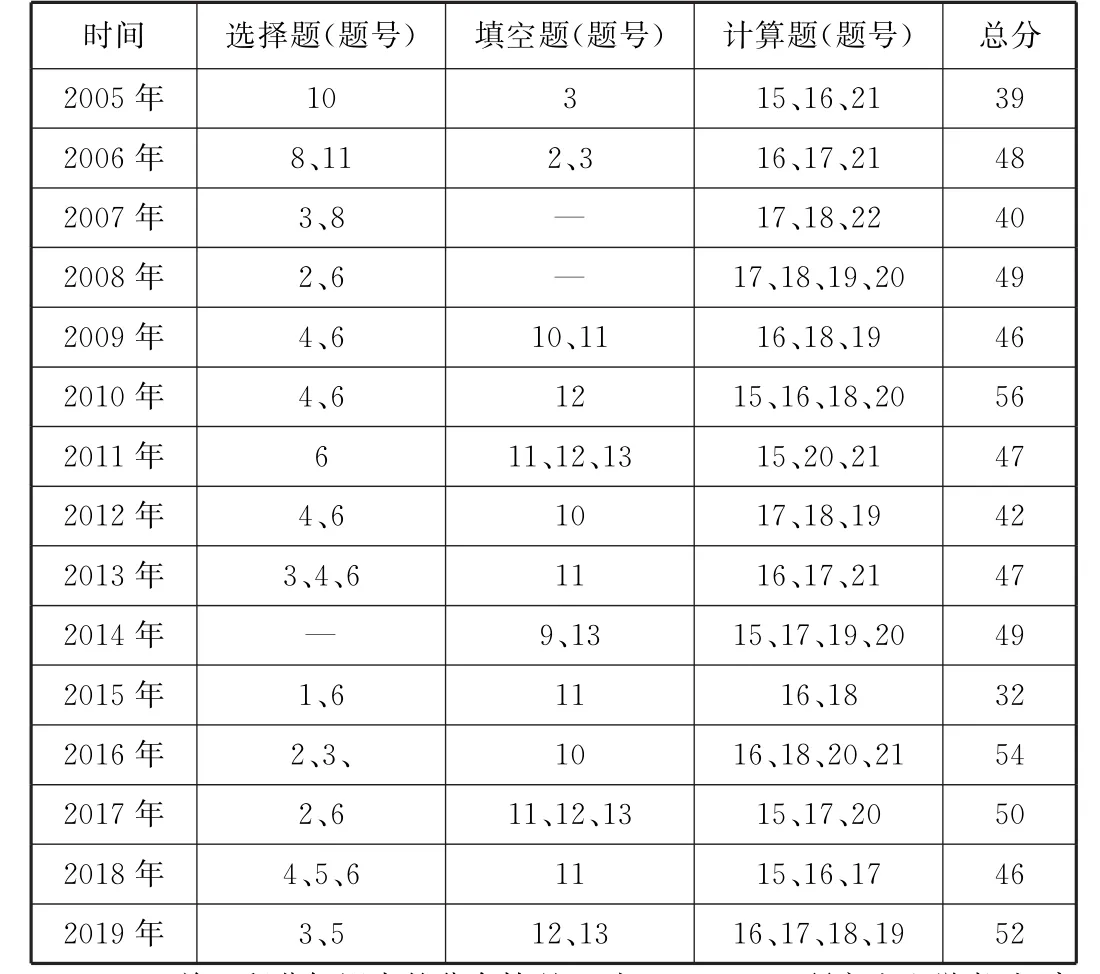
表2-1 2005—2019年研究生入學考試《高等數學II》中積分的題型和分值統計

2.2 關于積分知識點的分布情況 對2005-2019研究生入學考試《高等數學II》中有關積分的知識點進行統計見表3-2,得出如下兩個結論:(1)一元函數積分學主要考查不定積分的計算、不定積分的性質;利用定積分的定義求極限、定積分的計算、變上限積分的求導求極限、判斷變上限函數的單調性及其極值、積分中值定理和積分性質的證明及其應用、定積分的應用(如計算曲線的弧長、旋轉體的體積、平面薄片的重心坐標、轉動慣量、變力沿直線所作的功、水壓力的計算等);廣義積分的斂散性判別法及其計算;(2)多元函數的積分學主要包括利用二重積分的定義計算極限;二重積分在直角坐標系和極坐標下的計算;交換積分次序、累次積分等知識。

表2-3 2005—2019年研究生入學考試《高等數學II》中積分知識點分布情況

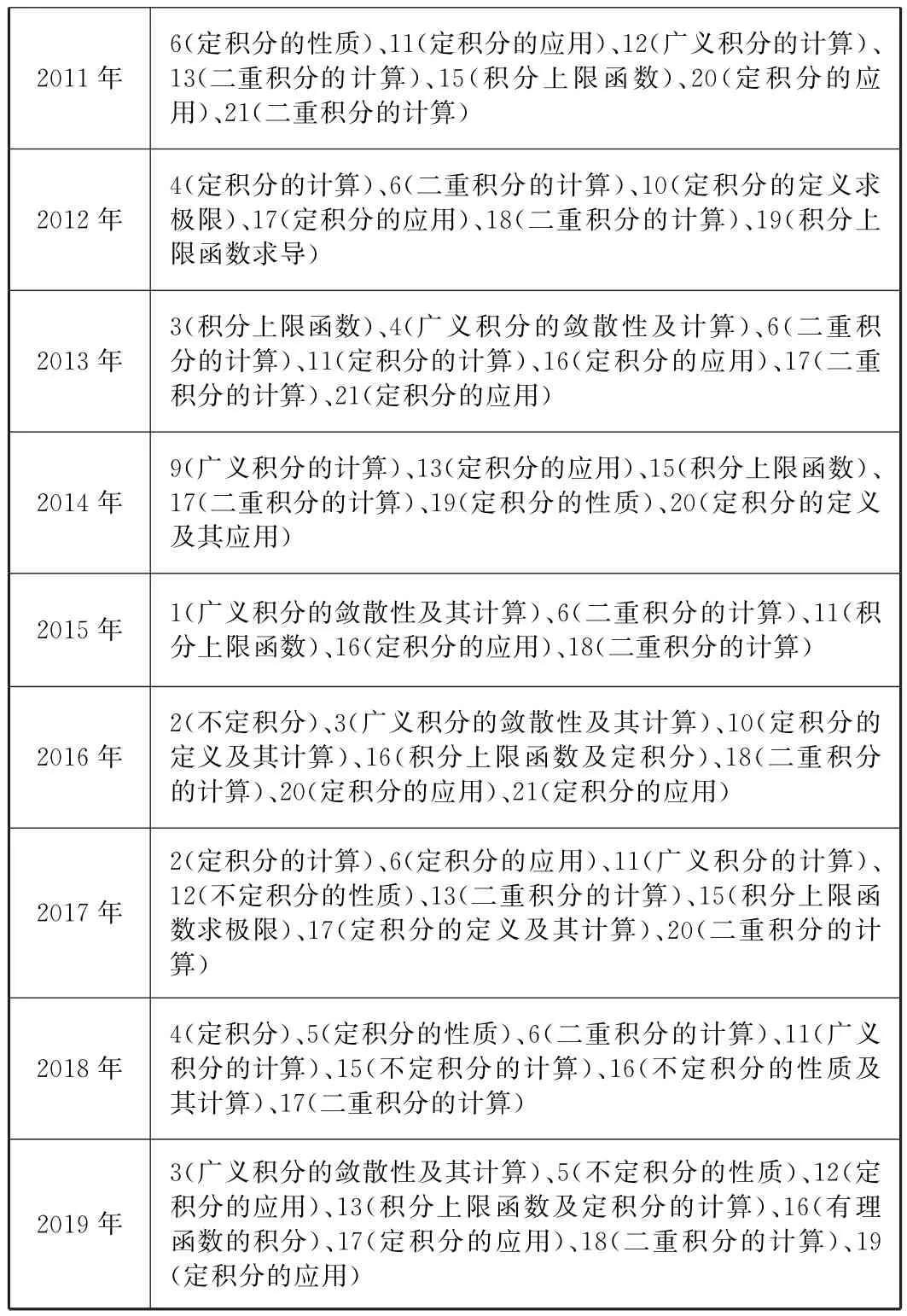
2011年6(定積分的性質)、11(定積分的應用)、12(廣義積分的計算)、13(二重積分的計算)、15(積分上限函數)、20(定積分的應用)、21(二重積分的計算)2012年4(定積分的計算)、6(二重積分的計算)、10(定積分的定義求極限)、17(定積分的應用)、18(二重積分的計算)、19(積分上限函數求導)2013年3(積分上限函數)、4(廣義積分的斂散性及計算)、6(二重積分的計算)、11(定積分的計算)、16(定積分的應用)、17(二重積分的計算)、21(定積分的應用)2014年9(廣義積分的計算)、13(定積分的應用)、15(積分上限函數)、17(二重積分的計算)、19(定積分的性質)、20(定積分的定義及其應用)2015年 1(廣義積分的斂散性及其計算)、6(二重積分的計算)、11(積分上限函數)、16(定積分的應用)、18(二重積分的計算)2016年2(不定積分)、3(廣義積分的斂散性及其計算)、10(定積分的定義及其計算)、16(積分上限函數及定積分)、18(二重積分的計算)、20(定積分的應用)、21(定積分的應用)2017年2(定積分的計算)、6(定積分的應用)、11(廣義積分的計算)、12(不定積分的性質)、13(二重積分的計算)、15(積分上限函數求極限)、17(定積分的定義及其計算)、20(二重積分的計算)2018年4(定積分)、5(定積分的性質)、6(二重積分的計算)、11(廣義積分的計算)、15(不定積分的計算)、16(不定積分的性質及其計算)、17(二重積分的計算)2019年3(廣義積分的斂散性及其計算)、5(不定積分的性質)、12(定積分的應用)、13(積分上限函數及定積分的計算)、16(有理函數的積分)、17(定積分的應用)、18(二重積分的計算)、19(定積分的應用)

3 復習建議

由于高等數學課程的特點,教師在課堂的講解非常重要,學生課后的學習也同樣重要。結合多年教學經驗和考研輔導經驗,提出《高等數學II》考研復習建議:

第一階段(2—3個月):基礎訓練。注重基本概念、基本理論、基本方法的復習與整理:這一個階段以課本為主,理解《高等數學》每一個概念、每一個定理、例題和習題全部都會做,同時歸納總結每一種題型的解題方法。這一階段關鍵理清楚《高等數學》知識脈絡和基礎內容知識,同時還需要掌握《高等數學》的基礎內容和典型例題推導出來的一些解題的關鍵結論,這些關鍵結論通常會在一些典型例題、習題和考題上出現,如果能熟練掌握這些關鍵結論,就能快速、正確的解題。

第二階段(2-3個月):提高訓練練習。這個階段必須建立在熟練掌握和理解《高等數學》基礎知識和方法的基礎上開展“做題式”訓練,可以購買一些《高等數學》考研相關的資料進行重復訓練,鞏固知識和方法。

第三階段(1-2個月):真題分析與方法總結。這一個階段可以選擇10—15年的真題進行分析與總結。首先選擇與正式考試相同的時間段做真題(注意中途不能休息不可以查閱相關材料,按照考試的要求進行,每天一份),考試結束后查閱參考答案對自己的考卷進行評閱,記錄自己的得分;其次對照參考答案分析自己的答卷,查找自己失分點;最后對查找出來的失分點,對照課本進行復習,再找相應題型進行訓練;注重歸納和總結真題考查知識的方式,反復歸納總結以提高《高等數學》成績。