旋轉分數階Fourier域構建SAR方位向成像算法的研究

王振力，王群，陳先意，馬如坡，劉曉遷

(1.江蘇警官學院 計算機信息與網絡安全系，南京 210031；2.南京信息工程大學 計算機與軟件學院，南京 210044)

0 引言

合成孔徑雷達(synthetic aperture radar，SAR)具有不受光照和氣候條件等限制實現全天時、全天候對地觀測的特點，可穿透地表或植被獲取其掩蓋的信息，在民用和軍事領域具有廣闊的應用前景。SAR通過把小孔徑天線雷達裝載在運動的載體上，利用雷達與地面測繪帶內各種目標的相對運動進而利用相干處理實現距離向和方位向成像[1]。常見的SAR成像算法[2]主要有距離多普勒(range Doppler，RD)算法、波數域(ωK)算法和CS(chirp scaling)算法等，其中距離多普勒算法[3-4]是SAR成像處理中最常見、最經典的方法。目前距離多普勒算法雖然在許多模式的SAR尤其是正側視SAR成像處理中仍然廣為使用，但是其較低質量的圖像越來越不能滿足實際應用需求[5-6]。

眾所周知，Fourier變換在傳統距離多普勒算法成像處理中起著至關重要的作用，而同時Fourier變換也是分數階Fourier變換(fractional Fourier transform，FrFT)階數為1時的特例。分數階Fourier變換是一種廣義的Fourier變換，它是一種統一的時頻變換，隨著變換階數從0連續增長到1而展示出信號從時域逐步變化到頻域的所有特征。將分數階Fourier變換應用于SAR成像處理是近年來的研究熱點[7-14]。文獻[7-8]針對線性調頻(linear frequency modulation，LFM)信號的參數估計問題,提出在分數階Fourier域進行二維譜峰搜索來確定分數階Fourier變換的最佳變換階數，該方法穩定性較好但搜索分數階譜峰計算量大，同時有限數據樣本會導致參數估計精度的降低。Capus 等[9]利用幾何變換關系得到適用于線性調頻信號的分數階Fourier變換[10]最優變換階數，但相應的分數階Fourier變換無法代替傳統距離多普勒算法中的Fourier變換進而實現信號重構。Mashed等[11]將分數階Fourier變換應用于傳統的RD算法，雖然可獲得SAR成像性能的提高，但同時計算復雜度也相應增加。陳勇等[12]通過局部最優處理來測量SAR回波信號的調頻率并以此計算FrFT的最優階數，所研究算法在提高彈載SAR成像性能方面是有效的但不具有適用的普遍性。為獲得地面運動目標清晰的SAR圖像，Tan等[13]提出分數階Fourier變換與自適應迭代模糊數算法相結合的多普勒參數估計方法；Wang等[14]提出聯合利用Wigner-Ville 分布和分數階Fourier變換實時估計多普勒參數的方法，并且觀測信號的WVD處理決定分數階Fourier變換的旋轉角；Huang等[15]利用距離-頻率變量的等間隔采樣，研究了基于RFRT-FrFT的合成孔徑雷達地面運動目標成像新算法。

本文針對傳統距離多普勒算法方位向成像質量低的問題，首先對SAR方位向信號進行變換分析得到其階數表達式；接著構建旋轉分數階Fourier變換域和方位向高分辨率成像算法；最后給出模擬數據和實測數據實驗結果與分析。

1 SAR方位向信號變換分析

在SAR成像系統中，理想的點目標回波在方位向近似為線性調頻信號的形式，如式(1)所示。

sa(t)=Wa(t)exp(j2πfdct+jπκat2)

(1)

式中：fdc為多普勒中心頻率；κa為方位向調頻率；Wa(t)=rect(t/Ta)；Ta為合成孔徑時間。連續信號f(x)的分數階Fourier變換定義式如式(2)所示。

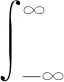
(2)

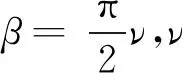
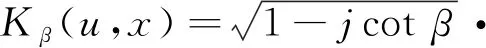
(3)

將式(1)代入式(2)，得到式(4)。

(4)

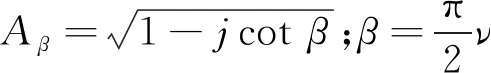
經簡化計算并利用駐定相位定理(principal of stationary phase)[16]，可得SAR回波方位向信號進行分數階Fourier變換時的最優階數，如式(5)所示。

(5)

式中：arctan(·)為反正切函數；Na為抽樣序列長度；Fa為抽樣頻率。對于實際SAR數據成像，Na長度既不可過大，也不可過小，否則會影響方位向成像質量，即方位向分辨率、方位向峰值旁瓣比(peak side lobe ratio，PSLR)和方位向積分旁瓣比(integrated side lobe ratio，ISLR)會受到相應的影響。

2 旋轉分數階Fourier變換域的構建

對于給定的SAR回波抽樣信號，方位向調頻率κa、抽樣序列長度Na和抽樣頻率Fa均是已知的，因此根據式(5)可直接計算出相應的最優階數νopt，相對應的時頻域旋轉角為β=-νopt×π/2。如圖1所示，其中負號表示逆時針旋轉，tν和fν分別表示方位向時間域和方位向頻率域。圖1中，yβ表示對方位向時域信號作旋轉角為β時的FrFT相對應的分數階Fourier變換域；yβ ′表示對分數階Fourier變換域yβ中信號作旋轉角為β′(β′=π/2，對應階數為1)時的FrFT相對應的分數階Fourier變換域;t′ν表示tν的平行軸，顯然tν⊥fν，yβ⊥yβ ′，方位向回波信號在時頻域(tν，fν)中分解形式與其在分數階Fourier變換域(yβ，yβ ′)中的分解形式是等價的，且后者更利于方位向回波信號能量的聚焦。若yβ域中分解信號等同于fν域中的頻率信號，則yβ ′域中分解信號等同于tν域中的時間信號。

圖1 方位向信號時頻域旋轉圖

3 方位向高分辨率成像算法的構建

無論機載或星載SAR成像，為提高方位向信號在分數階Fourier變換域中的成像聚焦效果，可將相應的時頻角旋轉π/2變換至(yβ ′，yβ ″)，此時方位向最優階數變為ν′opt=1-νopt，如圖2所示。圖2給出了以傳統距離多普勒算法為基礎的方位向成像算法的構建流程圖。由于多普勒中心頻率fdc在SAR正側成像模式下其值為0，式(5)是在此條件下得出的結論，因此依據此結論構建的算法與傳統距離多普勒算法的適用條件是一致的，即適用正側模式成像。

圖2 方位向高分辨率成像算法的構建流程圖

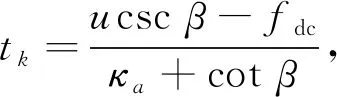
無論fdc是否等于0即正側模式還是斜側模式(小斜視角)成像，其對SAR成像精度均無影響，前提是fdc估計數值不能存在誤差。如果其數值存在誤差，方位匹配濾波器的中心頻率會偏離頻譜能量峰值，這會導致多普勒頻譜混疊最終出現圖像模糊。因此，本文算法也可適用于小斜視角條件下成像模式，這與傳統距離多普勒算法也是一致的。

4 數據成像實驗及分析

機載SAR正側視點目標成像仿真參數為：載波頻率為4 GHz，信號帶寬為120 MHz，信號脈寬為5 μs，信號抽樣頻率為192 MHz，脈沖重復頻率(PRF)為154 Hz，方位向天線尺寸為3 m，載機飛行速度為154 m/s，中心點斜距為5 000 m。仿真實驗中所選PRF的方位向過抽樣率系數為1.5，3個點目標幅度系數分別為0.8、1和1.2。對于采用傳統的RD算法、本文算法的3個點目標成像，由表1數據可知，在PSLR和ISLR相當的情況下，本文算法獲得的方位向分辨率絕對值降低0.42，相應的分辨率提高比值為31.3%。本文算法的方位向高分辨率成像在圖3和圖4中也能得到明顯體現。圖3所示的插值后點目標成像輪廓圖表明，經本文算法成像得到的點目標其方位向主瓣能量聚焦性能更優，相應的旁瓣能量明顯減弱。圖4 所示的插值后峰值點目標成像剖面圖表明，經本文算法成像的點目標其方位向波形主瓣寬度明顯變窄，旁(副)瓣電平也相應降低，因而其成像的清晰度得到顯著提高。

表1 方位向成像性能對比

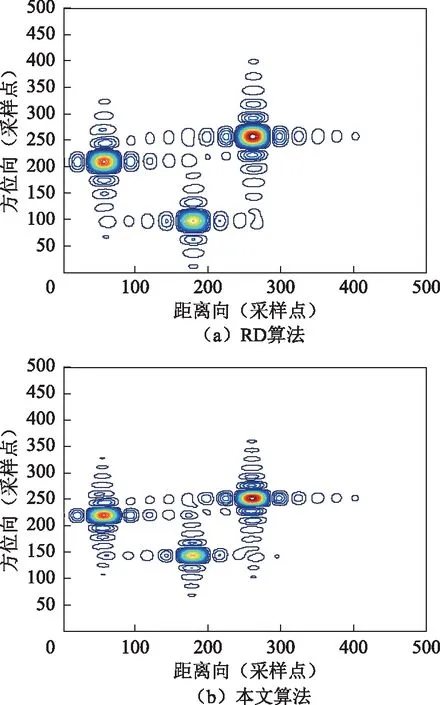
圖3 插值后點目標的輪廓圖

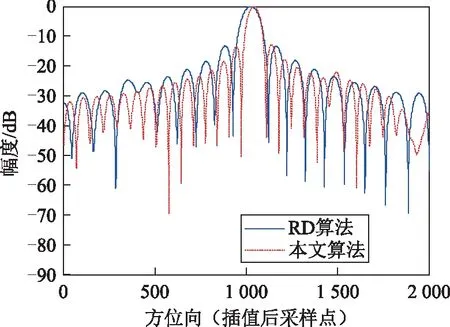
圖4 插值后峰值點目標成像方位向剖面圖

圖5給出了星載SAR實測數據成像結果，其原始數據來自于加拿大Radarsat-1精細模式下溫哥華場景(截取)。圖5成像結果表明：與傳統RD算法相比，經本文算法得到的SAR圖像分辨率高，所獲得的圖像中自然景觀公園、馬路和高速公路等清晰可見，斑點噪聲小，紋理和邊界線明顯，強點目標突出，強弱目標對比度高。圖6和圖7分別給出了與圖5相對應插值后的峰值點目標成像輪廓圖、峰值點目標成像方位向剖面圖，表2給出了方位向成像性能對比。由圖6和圖7可知，由本文算法成像的峰值點目標方位向主瓣寬度明顯變窄，旁瓣電平明顯降低，尤其是第一旁瓣能量顯著降低。由表2中實驗結果可知，在PSLR和ISLR相當的情況下，本文算法成像方位向分辨率絕對值比傳統RD算法降低12.12，相應的方位向分辨率提高比值為41.8%。

圖5 SAR實測數據成像

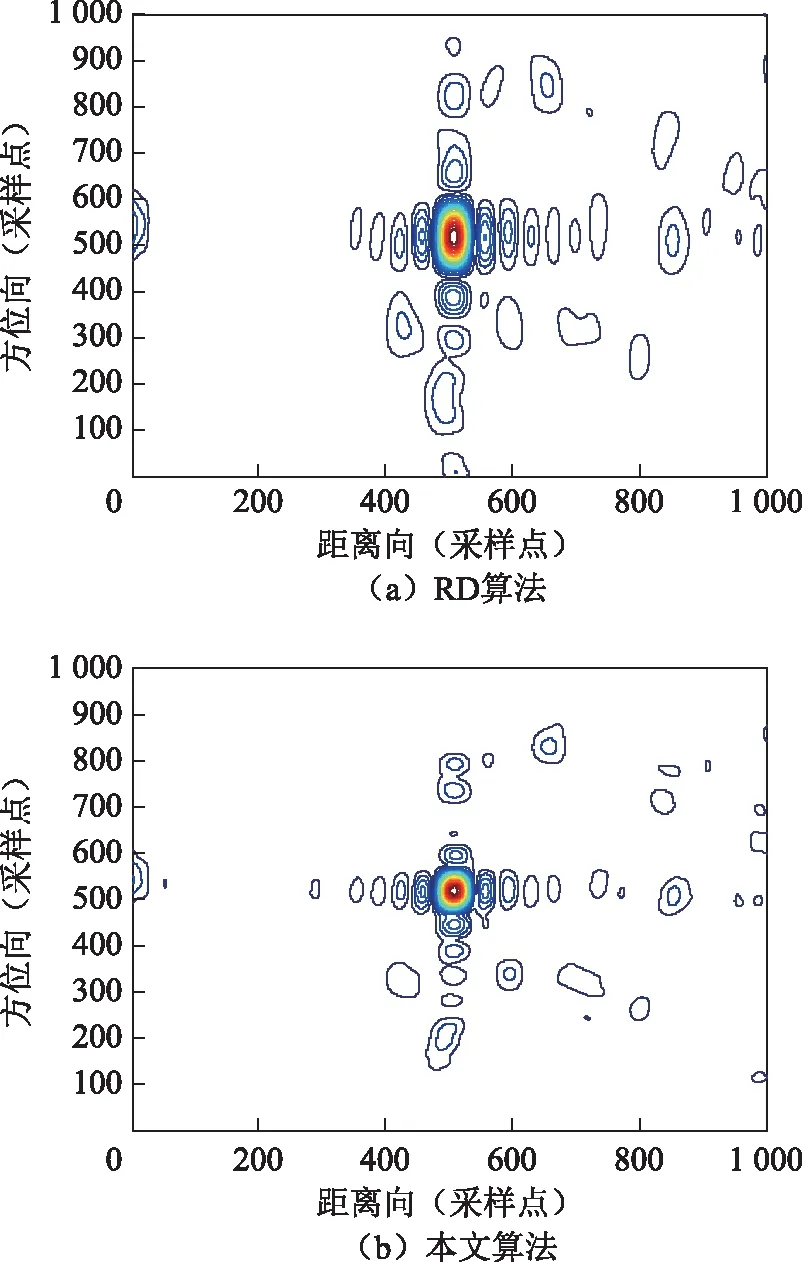
圖6 插值后峰值點目標成像輪廓圖

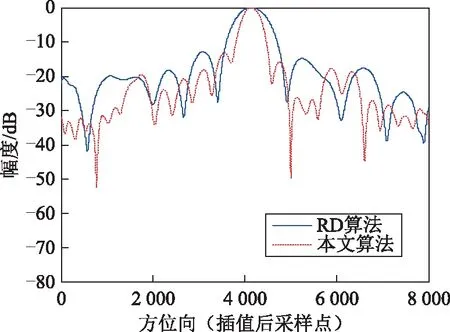
圖7 插值后峰值點目標成像方位向剖面圖

表2 方位向成像性能對比

以上機載SAR仿真數據和星載SAR實測數據成像實驗表明，由本文算法得到的SAR圖像均可獲得比傳統RD算法更優異的成像性能，這主要是因為本文算法在方位向依據最優階數獲得的旋轉分數階Fourier變換域(y′β1，yβ2)具有比傳統Fourier域更好的目標成像聚焦效果。

5 結束語

本文通過分數階Fourier變換的階數分析，建立SAR成像方位向最優階數計算表達式；以傳統的距離多普勒算法為原型，基于方位向最優階數獲得旋轉分數階Fourier變換域并提出方位向高分辨率SAR成像算法。機載SAR模擬數據和星載SAR實測數據成像結果表明，在峰值旁瓣比和積分旁瓣比相當的情況下，與傳統距離多普勒算法相比，本文算法得到的SAR圖像在方位向上的分辨率得到顯著提高，同時本文算法具有圖像斑點噪聲小、圖像紋理清晰和強弱目標對比度高等優點，因此更有利于SAR圖像目標的特征提取、目標識別、判讀與解譯。傳統的距離多普勒算法在方位向可看作本文算法的特例，二者計算量相當。本文算法的執行無需額外增加SAR載體平臺的任何硬件成本，具有良好的推廣應用價值。