基于模型預測的無人車路徑跟蹤優化控制

吳施鵬，劉冉冉，顏海彬，臧傳濤

（江蘇理工學院 汽車與交通工程學院，江蘇 常州 213000）

路徑跟隨是實現汽車自動駕駛的關鍵技術，其目的是控制汽車準確地跟隨目標路徑［1］。目前已有多種路徑跟蹤算法用于智能車輛的轉向控制［2］。應用較多的有純點追蹤算法［3］、線性二次型調節器跟蹤控制器［4］、嵌套式PID控制算法［5］以及預瞄跟蹤最優控制等［6］。然而，在現實控制中這些算法存在忽略行駛時車輛動力學約束的問題，而模型預測控制以準確的動力學模型作為預測模型，在控制時加入約束條件，具有提高控制器對車輛未來行為的預測能力的優勢［7］。所以，本文中選用模型預測控制方法。

模型預測控制在實現過程中有模型預測、滾動優化和反饋校正3個關鍵步驟［8］。模型預測控制最明顯的優點是能在控制過程中增加多種約束。無人車輛在低速時，車輛平臺運動學約束影響較大，而隨著速度的增加，動力學特性對運動規劃與控制的影響就越明顯，帶來多種模式的約束，這正是模型預測控制在無人車輛運動規劃控制方面的應用優勢［9］。國外的Falcone等［10］在線性車輛模型基礎上設計了MPC控制器并將其用于路徑跟蹤系統，實車上對控制算法進行了驗證。Abbas等［11］在非線性車輛模型的基礎上設計MPC控制器，綜合考慮了路徑跟蹤過程中輪胎的側偏角約束，但是存在實時性較差的問題，且對系統的硬件設備要求較高。Sara Mata等［12］提出了一種基于預測模型和保證穩定性的MPC路徑跟蹤控制器。該方法優化了橫向位移和偏航角，提供了更精確的路徑跟蹤。J Ji等［13］在MPC方法中，以約束條件下的成本最小化為優化問題，輸入側向位置、橫擺角速度、側滑角和方向盤轉角等約束來提高高速下的車輛穩定性。Garcia O等［14］提出了一種利用MPC設計和仿真路徑跟蹤控制的方法，控制器的設計模型基于車輛的單一跟蹤模型和由卡爾曼濾波器觀測狀態變量的轉向模型。Arun等［15］提出了一種基于MPC的自動駕駛控制系統，該系統采用圖形處理單元，提高了計算速度和系統的實時性。武漢理工大學的張嚴等［16］建立了縱向、橫向和橫擺的3自由度汽車動力學模型，確定目標函數并加入約束條件，利用遺傳算法對模型預測控制器的預測時域、控制時域進行優化。但在較高車速和較大道路彎曲曲率的路徑下仍然有較大的偏差量。北京工業大學的段建民等［17］通過改進目標函數、增加輪胎側偏角動力學約束，以車輛動力學模型作為模型預測控制的預測模型，提出了一種改進的智能汽車目標路徑跟蹤方法，但其在高速情況下仍然會出現較大的側滑，導致跟蹤出現偏差。遼寧工業大學的李金良等［18］驗證了線性時變模型預測控制算法在低速下的路徑跟蹤效果，說明這個方法在低速下軌跡跟蹤有較好的實時性以及行駛穩定性，但是沒有驗證這種控制算法在高速下的路徑跟蹤效果。雖然現在模型預測控制有著比較成熟的理論，但是其在低路面附著系數和高速工況下的軌跡跟蹤效果并不理想。

為了解決上述問題，提高模型預測控制器在各種工況下的跟蹤性能和行駛穩定性。通過建立2自由度汽車動力學模型，設置模型預測控制的目標函數，進而對建立的目標函數進行求解，利用遺傳算法優化控制器參數來提高車輛的跟蹤精度，最后在控制器中加入前輪側偏角軟約束，既保證了車輛在高速工況下的跟蹤精度，又保證了車輛的行駛穩定性。

1 車輛動力學建模

1.1 車輛2自由度單軌模型

本文中建立整車動力學模型，研究路徑跟蹤的魯棒性和實時性，重點考慮車輛縱向、橫向以及車輛橫擺動力學特性［19］。為了簡化模型的復雜程度，以減小計算量，假設汽車在平坦的路面上行駛，忽略車輛垂向運動和懸架運動，不考慮車輛載荷左右轉移［20］。據此建立的2自由度車輛動力學單軌模型如圖1所示。

根據圖1可以得到以下的關系：

建立車輛的受力平衡方程：

式中：X、Y為質心橫縱坐標值；x、y為質心縱橫向位移；a、b為前后軸至質心的距離；m為整車質量；Fyf、Fyr、Fxf、Fxr分別為前后輪所受的橫縱向力；φ為車輛航向角；Iz為車輛繞z軸的轉動慣量。

車輛的輪胎在x、y方向所受到的力為：

式中：Fxf、Fxr為輪胎在x方向所受到的力；Fyf、Fyr為輪胎在y方向所受到的力；Flf、Flr為輪胎所受縱向力；Fcf、Fcr為輪胎所受橫向力；δf、δr分別為前后輪轉角。

1.2 輪胎模型

車輛在側偏角和側向滑移率較小的情況下輪胎力可以用線性函數來表示［21］。輪胎的縱側向力通過下式來計算：

式中：F1為輪胎縱向力；Fc為輪胎側向力；C1為輪胎縱向剛度；Cc為輪胎側偏剛度；s為輪胎滑移率；α為輪胎側偏角。

輪胎前后側偏角為：

可以得到車輛的前后側向力和縱向力：

式中：Ccf、Ccr為前、后輪側偏剛度；C1f、C1r為前后輪胎縱向剛度；Sf、Sr分別為前后輪胎縱向滑移率。

可以得到車輛在前輪偏角很小的狀態下的動力學模型：

2 MPC控制算法設計

2.1 預測模型建立

式（7）為建立的非線性動力學模型，但其不能直接用于線性時變模型預測控制，因此需要對非線性系統進行線性化處理。

參考系統在任意時刻的狀態量與其在某一時刻的狀態量及控制量有關，在此將其表示為：

泰勒公式的形式為：

此處忽略泰勒公式的高階項，只保留其一階項，可以得到：

將式（10）和式（8）相減得到：

簡化其線性時變方程為：

上述所建立的線性化模型為：

設模型預測控制中的2個時域參數為Np，Nc，則控制器能夠預測到系統的狀態量為：

2.2 預測模型求解

在車輛高速行駛時易產生控制量突變的情況，使跟蹤軌跡完全偏離目標軌跡，因此，在目標函數中加入松弛系數來解決此問題，故采用如下形式設計模型預測控制器的目標函數［22］：

式中：η（t+i｜t）為系統的實際輸出軌跡；ηr（t+i｜t）為系統的參考輸出軌跡；Δu（t+i｜t）為控制量的變化；Q、R為權重矩陣；Np為預測步長；Nc為控制步長；ρ為權重系數；ε為松弛因子，當跟蹤誤差較小時取較大值，跟蹤誤差較大時取較小值。

式（16）中的第1項表明設置參考路徑后的車輛跟蹤效果，第2項表明控制量的變化平穩性，第3項加入松弛系數，來對約束范圍進行調節，防止該方程無法在硬性約束下求得最優解。

因此，模型預測控制器需要求解目標函數的最小值，以得到最優解，即：

在每個控制步長中，需要對系統的控制量進行約束。

控制量約束：

式中，k＝0，1，…，Nc-1。

控制增量約束：

式中，k＝0，1，…，Nc-1。

綜合考慮目標函數和約束條件后，需要在每個周期內解決以下優化問題：

式中：ΔUmax、ΔUmin為控制增量最大值和最小值。αmax、αmin為軟約束輸出最大值和最小值。

2.3 反饋校正機制

對上述問題進行求解可獲得每個時域內的控制增量。將每個時域內的控制增量表示為：

因此，系統實際接收到的輸入量為：

不斷地循環進行這樣一個過程，就可以讓控制器實時地跟蹤到目標軌跡。其控制原理如圖2所示。

3 控制器優化

3.1 遺傳算法優化

由于模型預測控制器中時域參數Np和Nc的取值能夠大大影響無人駕駛車輛的路徑跟蹤性能，為了能夠獲得最優的時域參數，本文中通過遺傳算法對時域參數進行優化。遺傳算法是一種成熟的優化算法，其利用適應度函數來判斷解的好壞。

采用如下的遺傳算法步驟對時域參數Np和Nc進行優化：① 初始化種群，生成N個個體的初始基因；②選用適應度函數來評估種群個體適應度，計算出個體的適應度值；③選出適應力強的個體進行遺傳和交叉，生成新的個體。遺傳算法會隨機地選擇少數個體進行變異操作，以避免優化結果陷入局部最優［23］。本文中根據文獻［24］，設置遺傳算法的種群大小為50，終止進化次數為20，交叉概率為0.6，變異概率為0.1。設置優化變量為系統的時域參數Np、Nc。時域參數的優化原理如圖3所示。

因為系統的橫縱向偏差屬于不同數量級，因此將其量綱為一化處理：

將橫縱向偏差進行加權組合：

式中：σ為權重系數，取值范圍為（0，1），本文中取σ＝0.7。

時間乘以誤差絕對值積分（ITAE）性能指標是一種具有很好的工程實用性和選擇性的控制系統性能評價指標［25］。因此本文中的適應度函數選用ITAE指標：

由于考慮到模型預測控制器中的預測時域和控制時域必須為整數，因此在遺傳算法中隨機初始化種群時加入round函數讓種群變為整數，避免遺傳算法無法尋找到最優解的情況，再輸入到模型預測控制器中。在Simulink下建立模型，如圖4所示。

3.2 前輪側偏角約束優化

需要將前輪側偏角控制在合適的范圍內，來保證輪胎的側偏角和側偏力呈線性關系。本文中研究在低附著系數和較高行駛車速工況下的路徑跟蹤，側偏角對路徑跟蹤性能有較大的影響，所以將前輪側偏角軟約束的范圍設置為-2.82°≤α≤2.82°。

本文中設置的系統控制量為前輪轉角，其變化范圍對路徑的跟蹤效果有較大影響，因此需要約束前輪轉角及其變化范圍，設置其范圍為：

4 仿真結果

選用文獻［9］中傳統模型預測控制的無人駕駛車輛基本參數，在Carsim車輛動力學仿真軟件中車輛的基本參數見表1。控制器部分仿真參數見表2。

表1 動力學模型基本參數

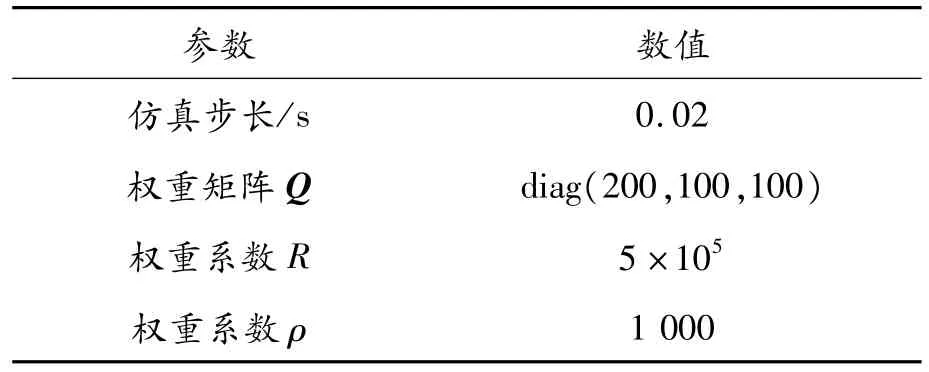
表2 控制器部分仿真參數

采用Carsim和Matlab／Simulink進行聯合仿真，設定的參考軌跡為雙移線路徑，在附著系數為0.4和0.85的路面進行仿真，分別對比50 km／h和100 km／h車速下傳統MPC、經遺傳算法優化后的MPC以及加入前輪側偏角軟約束后的路徑跟蹤效果。

無人駕駛車輛在 μ＝0.85、v＝50 km／h下的仿真結果如圖5所示。

由圖5可知，在附著系數為0.85、車速為50 km／h下的3種控制器均具有較高的控制精度。經過遺傳算法優化后的控制器路徑跟蹤誤差略微低于傳統MPC，其路徑跟蹤精度稍微好于傳統MPC。相比于文獻［16］中僅通過遺傳算法優化的方法，本文中加入前輪側偏角約束，其路徑跟蹤誤差和橫擺角更大一點但差別很小，這說明3種控制器的橫擺角相差不大，在高附著中速情況下3種控制模式的行駛穩定性很接近，路徑跟蹤性能變化不大。

無人駕駛車輛在 μ＝0.4、v＝50 km／h下的仿真結果如圖6所示。

由圖6可知，在附著系數為0.4、車速為50 km／h的情況下，經過遺傳算法優化后的路徑跟蹤精度更高一些，但其在行駛到90 m處車輛出現短暫的波動，隨后可以調整過來繼續跟蹤到路徑。相比于文獻［16］中僅通過遺傳算法優化的方法，本文中加入前輪側偏角約束，其路徑跟蹤誤差與文獻［16］方法下的路徑跟蹤誤差差別不大，但其橫擺角并未產生波動。這也說明后2個控制器的路徑跟蹤誤差要好于傳統的MPC，而加入了前輪側偏角約束后的車輛的行駛穩定性要高于傳統MPC和加入遺傳算法后的MPC。

無人駕駛車輛在 μ＝0.85、v＝100 km／h下的仿真結果如圖7所示。由圖7可以看出，在μ＝0.85、v＝100 km／h的工況下，傳統MPC控制最開始能跟蹤到參考軌跡，但在90 m之后出現了遠離參考軌跡的情況，并在100 m之后出現波動，控制器輕微失穩，可以知道傳統的MPC在高附著高速的路面狀況下的軌跡跟蹤效果并不好。而遺傳算法優化后在一定程度上軌跡跟蹤的誤差減小，在前100 m處能夠較好地跟蹤到軌跡，但在125 m之后出現了控制器失控的現象，無法很好地跟蹤到軌跡。再加入前輪側偏角約束之后可以看出，無人駕駛車輛在前90 m處的運行很平穩，而且對參考軌跡具有一定的跟蹤能力，尤其是在90 m之后，無人駕駛車輛對參考軌跡的跟蹤誤差越來越小，最終可以完全跟蹤到參考軌跡。并且加入了前輪側偏角約束控制下的車輛橫擺角波動要遠遠小于前2個控制器下的車輛橫擺角。相比于文獻［16］中僅通過遺傳算法優化的方法，本文中加入前輪側偏角約束后的路徑跟蹤誤差和橫擺角都要遠遠小于文獻［16］方法下的路徑跟蹤誤差和橫擺角，這說明在高附著系數高速下加入前輪側偏角約束控制器的行駛穩定性要遠遠優于傳統MPC和加入遺傳算法優化后的控制器。

無人駕駛車輛在 μ＝0.4、v＝100 km／h下的仿真結果如圖8所示。

可以看出，μ＝0.4、v＝100 km／h的工況下，傳統MPC無法跟蹤到路徑，控制器完全失控，傳統MPC在低附著和較高速度下對參考軌跡沒有跟蹤能力。經過遺傳算法優化后的無人駕駛車輛在前60 m處對軌跡具備一定的跟蹤性能，但在80 m處出現了無人駕駛車輛無限偏向一方的情況，控制器在前期對參考軌跡還具有一定的跟蹤能力，但在后期已經無法跟蹤到參考軌跡。相比于文獻［16］中僅通過遺傳算法優化的方法，本文中加入前輪側偏角約束，無人駕駛車輛可以較好地跟蹤到軌跡，控制器并沒有出現失穩的情況，橫擺角的變化較為平穩，也說明附著系數較低的路面高速行駛時加入前輪側偏角優化后控制的車輛的行駛穩定性明顯優于傳統MPC算法和加入遺傳算法優化后的車輛。

5 結論

為了解決無人駕駛車輛在低附著系數和高速工況下路徑跟蹤效果和行駛穩定性差的問題，本文中提出了一種基于模型預測的無人車路徑跟蹤優化控制方法。在高附著系數和中速的工況下利用遺傳算法尋找出控制器的最優時域參數來減小無人駕駛車輛的路徑跟蹤誤差，再在低附著系數和高速的工況下利用遺傳算法和加入前輪側偏角軟約束來提升無人駕駛車輛的跟蹤性能，通過Carsim和Matlab／Simulink進行聯合仿真。仿真結果表明：在高路面附著系數和中速的工況下，利用遺傳算法可以減小路徑跟蹤誤差，提高車輛的行駛穩定性。在低路面附著系數或者高速的工況下，聯合應用遺傳算法和前輪側偏角約束能夠大大減小無人駕駛車輛的路徑跟蹤誤差，提高行駛穩定性，控制器具有較高的路徑跟蹤精度。車輛在低附著系數下高速行駛時能夠保持一定的跟蹤精度，并同樣可以保證一定的行駛穩定性。本文中方法可以拓展應用到對無人駕駛系統權重矩陣優化和對后輪轉角控制算法設計方面。但對于實際的車輛系統，其參數是非線性變化的，并且變量信息不一定能夠實時獲取，可以在后續研究中采用非線性模型預測控制系統，并且考慮系統的時滯對跟蹤效果的影響。