面向結腸鏡軟體機器人設計與建模仿真

陳 剛，鄔元富，李 偉，李緣春，王依濤

（1.嘉興學院 機電工程學院，浙江 嘉興 314000；2.廣西財經學院 經濟與貿易學院，南寧 530007）

當今生活節奏越來越快、人們的飲食結構和生活方式發生了較大的變化，癌癥的發病率也不斷增加，其中結直腸癌發病率呈現明顯上升趨勢，在2002—2015年里發病率由7%上升至13%［1］，目前位居我國癌癥發病率第4位。結腸鏡檢查是結腸癌檢測諸多方法中最為可靠、有效的一種，不僅可以進行細胞切片取得病理診斷，而且可以對病灶進行定位、診斷病灶大小。目前的插入技術迫使外科醫生在器械的遠端對結腸鏡末端部進行控制［2］。然而在進行結腸鏡檢查中，由于結腸鏡末端部無法實現自主控制，在結腸鏡推進與取出的過程中，結腸鏡末端部容易與腸壁發生不必要的接觸，導致結腸粘膜的損傷出血甚至腸壁穿孔［3］。

為了減少患者的不適、降低結腸檢查過程中的操作難度，許多研究者選擇了自動結腸鏡檢查的方法。在文獻［4］中，作者基于結腸鏡檢查的2個主要動作，即遠端運動和轉向，提出了自動結腸鏡檢查（也稱為機器人結腸鏡檢查）的概念。目前，關于自動結腸鏡檢查的研究大多集中在利用各種運動機構的自推進機器人上，還有一些研究者們致力于研發無線膠囊結腸鏡檢查，用于圖像診斷或復雜多參數檢測［5-11］。其中，蠕動運動的推進方式研究較為廣泛。然而，目前大多數基于蠕動的機器人系統，存在以下2個問題：①結腸內部是一個受限的三維空間，關于結腸鏡模型的運動規劃方面的研究非常少［12］；② 結腸內壁表面光滑，在探索結腸時常表現出較低的運動效率。

針對這些問題，本文提出了一種新型可彎曲結腸鏡末端結構設計，在相隔120°的方向上各布置一個氣動腔室，以實現各個方向的彎曲；再對該軟體機器人在輸入氣壓作用下的末端部位置進行分析，利用幾何方法建立了其運動學模型，可為軟體機器人控制規律的設計與路徑規劃提供控制模型；最后進行三維仿真模擬結腸鏡軟體機器人彎曲動作，并搭建實驗平臺進行驗證。

1 結腸鏡機器人末端部結構設計

在設計結腸鏡機器人末端時，應著重考慮2個方面。第一個方面，此結構應該有足夠的剛度來支撐機器人的運動；第二個方面，結構應具有良好的抗彎性能［13］。考慮到這些問題，本文提出了一種三腔驅動末端，它是一個可獨立運動的單元，內置3個間隔120°的腔體。頂端橫截面外徑為16 mm，小于結腸的平均直徑。內孔直徑為5 mm，用于放置相機等其他照明工具，橫截面結構如圖1所示。每個氣室的內部壓力可以使用氣動伺服閥獨立控制。

2 結腸鏡機器人末端部的運動學分析

為了控制機器人末端部的形狀，了解機器人頂端的位置與其控制輸入之間的關系是必要的。本文在幾何學分析與常曲率運動學的基礎上建立其運動學模型，常曲率運動學優點在于將運動學轉換分解成2個獨立的映射：一個從執行器空間到配置空間；另一個從配置空間到任務空間。前者依賴于機器人的實際結構設計，后者則適用于所有符合常曲率假設的設計［14］。當結腸鏡機器人受力時，會向某個方向彎曲，可以將其中心線與腔室中心線看作若干段常曲率圓弧［15］，用φ表示其彎曲的角度，Φ表示其彎曲方向。其中，A所在陰影表面為軟體機器人的上表面，A面與XY平面的夾角為φ，機器人彎曲運動參數如圖2、3所示，其參數含義見表1。

表1 參數含義

當負載影響被忽略并且偏轉角度φ處于0＜φ＜π時，處于彎曲狀態的的軟體機器人的形狀可被假定為一個圓弧。鑒于這一假設，顯然

結腸鏡機器人中心線在底面上的投影與Y軸負方向夾角為Φ，底面與上端面A的相交線為l，則底面腔室圓心到相交線l的距離為Ri，如圖2所示。則各腔室中心線相對于彎曲平面的角度為：

利用這些角度，可以將腔室i的曲率半徑描述為：

并結合方程（3）（4）可推導出方向角：

同時，中心線的曲率半徑和彎曲角φ可表示為：

利用上文確定的運動模型，各腔在壓力變化下的對應長度可以表示為：

因此，可將機器人形狀參數與輸入壓力的正運動學方程表示為：

在假定機器人的彎曲形狀為圓弧的前提下，通過圓柱坐標變換，可得到機器人在任務空間中末端與機器人彎曲參數相關的笛卡爾坐標（x，y，z）

由此可給出該模型的狀態空間：

其中X＝（φ，φ，L）T，QP＝（P1，P2，P3）T。

3 三維模型與仿真

3.1 模型選擇

有限元法廣泛地運用于物體的應力、應變分析，模擬物體的物理行為等領域。然而在進行大變形柔性體模擬仿真時，描述應變與位移之間的幾何關系發生了變化，因此有限元法在對軟體機器人建模仿真中存在著諸多不便。

本次仿真選用專門用于模擬大變形柔性材料的軟件包VoxCAD。VoxCAD與傳統有限元軟件的主要區別在于其使用的是質點-彈簧法模型，基于“歐拉-伯努利梁理論”，將對象分解為由梁單元所連接的立方體單元，如圖4所示，每個立方體單元儲存有質量和轉動慣量；梁單元則儲存有平移和轉動剛度［16］，不僅能夠計算拉伸壓縮，還將所有軸的橫向剪切和旋轉考慮進去。

3.2 建立質點-彈簧模型

首先建立一個16×16×110的工作區域，共計28 160個體素。材料模型視作線性材料，具有各向同性，各材料屬性由查詢相關資料填入，有關參數如表2所示。其中，深色體素直接受力，淺色材料不直接受外力，在相鄰體素的彈簧力作用下位置發生相應改變，最終建立一個具有3個腔體的空心圓柱體，如圖5所示。

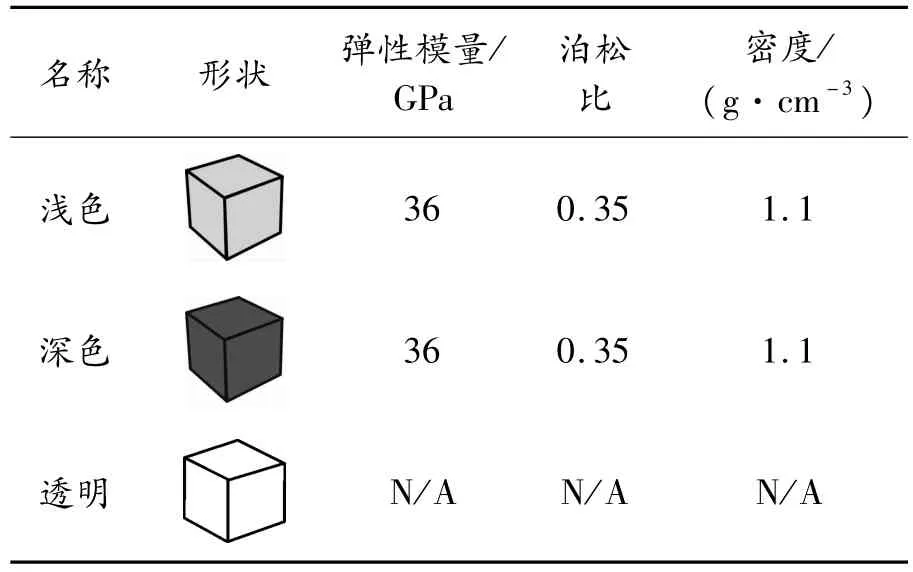
表2 材料參數

3.3 物理仿真

對氣動軟體機器人彎曲的過程進行仿真，為簡化計算，假定軟體機器人只有單側腔體處于充氣狀態，因而軟體機器人會因徑向不平衡力發生彎曲。為此，將三維模型底面固定，即底面所有體素自由度為0。腔體內壁體素（所有深色單元）受到垂直于空腔內表面的壓力，環境設置中引入重力。模型變形的運動如圖5、6所示，在0.7 MPa的壓力下，模型最大伸長量為30.7 mm，伸長量與到底面的距離成正相關。充氣腔室在壓力下向外膨脹，壓力大小與到充氣腔室的距離成負相關，仿真變形結果如圖6、7所示。仿真模型與運動學模型的數據分析將在4.2節中給出。

4 實物驗證

4.1 實驗平臺的搭建

為驗證三維仿真與運動學模型的有效性，需搭建實驗平臺用以測試。本次實驗通過控制氣動回路內部的氣壓來實現軟體機器人的運動，可分為兩大部分：控制回路與氣動回路。實驗平臺系統實物如圖8所示。

控制回路：上位機編寫程序上傳至Arduino板卡，Arduino板卡輸出開關信號至繼電器，由繼電器輸出12 V電壓控制電磁閥開閉，從而控制軟體機器人的3個并聯氣體腔室的通氣與否。Arduino板卡輸出PWM信號，經過電壓轉換模塊轉變為0～12 V的電壓控制電氣比例閥，比例閥可輸出對應氣壓來達到控制軟體機器人運動的效果。

氣動回路：氣體從空氣壓縮機進入氣動三聯件，先經過調速閥以調節流速大小，再經過電氣比例閥調節出口壓力，最終得到滿足實驗所需的氣體接入3個3位五通電磁換向閥，每個電磁閥各自與一個腔室相連，由換向閥控制軟體機器人空腔的進氣與放氣。

4.2 實驗結果的分析

在壓力范圍0～0.12 MPa的條件下進行實驗，每隔0.03 MPa記錄一次氣壓與末端位置，共5個位置。為了更為直觀地對比理論位置與實際位置的差異，可以用5個離散點得到一個連續曲線用以比對，由于實驗采集離散點較少，且目標曲線的部分自變量對應2個應變量，因此無法用初等函數將曲線標書出來，故放棄使用函數來擬合或逼近，選用多項式樣條插值法。本文通過Matlab三次樣條插值得到其樣條曲線［17］。

實驗樣機運動軌跡如圖9所示，各模型末端軌跡如圖10所示。圖中樣條曲線穿過5個離散點經樣條插值法所得，理論曲線為第2節中的運動學模型在0～0.12 MPa下所得機器人末端坐標的樣條曲線，仿真曲線為VoxCAD中模型在壓力范圍0～0.12 MPa下的末端運動軌跡。

如圖10所示，在壓力范圍0～0.03 MPa下，實驗樣機曲線、運動學模型曲線基本相同；在氣壓逐漸增大后，樣機位置漸漸偏離理論位置，但趨勢大致相同。造成上述誤差的主要原因有：軟體機器人材料并非均質材料，液態硅橡膠攪拌過程中難以做到絕對均勻，且在凝固過程中不均勻部分與雜質部分會在重力作用下發生沉淀，進一步導致材料的密度不均。因此，軟體機器人的運動誤差會隨著氣壓的增大而累積。另外，實物模型充氣腔室的位置誤差也會對其運動結果造成影響。

質點-彈簧模型曲線與運動學模型曲線大致吻合，這進一步驗證了理論的正確性。但誤差仍然存在，且有著隨壓力增大而增大的趨勢，主要原因在于等曲率模型僅從運動學層面進行研究，在實驗樣機與三維模型中，會引入重力、彈性變形力等動力學因素，其軸線并不嚴格符合弧線的假設［18］。

5 結論

本文中設計了一種新型的可彎曲結腸鏡機器人，末端的外徑為16 mm，小于結腸的平均直徑（20 mm），建立了運動學模型，利用彈簧-質點法建立了三維模型并進行可視化仿真，驗證了運動學模型的正確性。提出了新的方法對軟體機器人進行可視化仿真，展示了軟體機器人末端在單腔驅動情況下的運動結果，解決了以往大變形柔性體難以仿真的問題。

軟體機器人具有良好的柔性與適應性，十分適用于醫學診斷檢測、勘探偵查等領域。軟體機器人建模與控制方法關乎其形狀控制精度，目前分段常曲率法是軟體機器人運動學建模領域最常用的方法，但此方法僅從運動學層面進行研究，沒有考慮彈性變形力、重力等動力學因素的影響，無法應用到結構形狀更加復雜的軟體機器人建模，還存在較大改進空間。