液壓擺臂履帶可變形機器人的設計*

□ 孫英暖 □ 孟廣耀 □ 王 哲 □ 王維信

青島理工大學 機械與汽車工程學院 山東青島 266520

1 設計背景

機器人能代替人類從事很多危險的工作,如消防救火、爆破排障等。機器人的行走機構一直是眾多科研工作者關注的問題。機器人行走機構主要有輪式、腿式、履帶式三種。其中,輪式行走機構越障能力差,不能在復雜的地形中工作;腿式行走機構行走速度有限,不能實現快速作業;履帶式行走機構能適應復雜的環境,具有較快的移動速度,被廣泛使用。當然,機器人履帶式行走機構也有缺點,履帶長時間過緊會拉長鏈軌節,過松會影響驅動,而且容易掉鏈。

目前,已有學者致力于機器人履帶式行走機構的研究,并對其進行改進。朱巖等[1]利用凸輪機構,研制出履帶能持續張緊且長度保持不變的SARTR機器人。文獻[2]利用橫縱軸雙導軌,實現履帶持續張緊且長度保持不變。筆者將機器人履帶式行走機構的后擺臂設計為由小型液壓系統結合可編程序控制系統控制,代替凸輪及橫縱軸雙導軌,得到液壓擺臂履帶可變形機器人,同樣可以實現履帶持續張緊且長度保持不變,同時具有較高的實時性與穩定性,保證越障時翻越障礙與履帶持續張緊的同步性,極大提高了機器人的越障平順性。

2 后擺臂構形原理

液壓擺臂履帶可變形機器人與不可變形機器人相比,具有更高的穩定性及越障能力,但設計也更為復雜,主要是解決如何在維持履帶張緊力不變的情況下,盡量保持履帶長度不變的問題。針對這一問題,筆者將橢圓定理應用于履帶式行走機構的設計,使后擺臂運行軌跡為橢圓,并使用彈簧作為輔助機構,與液壓系統控制相結合。

后擺臂構形原理如圖1所示。

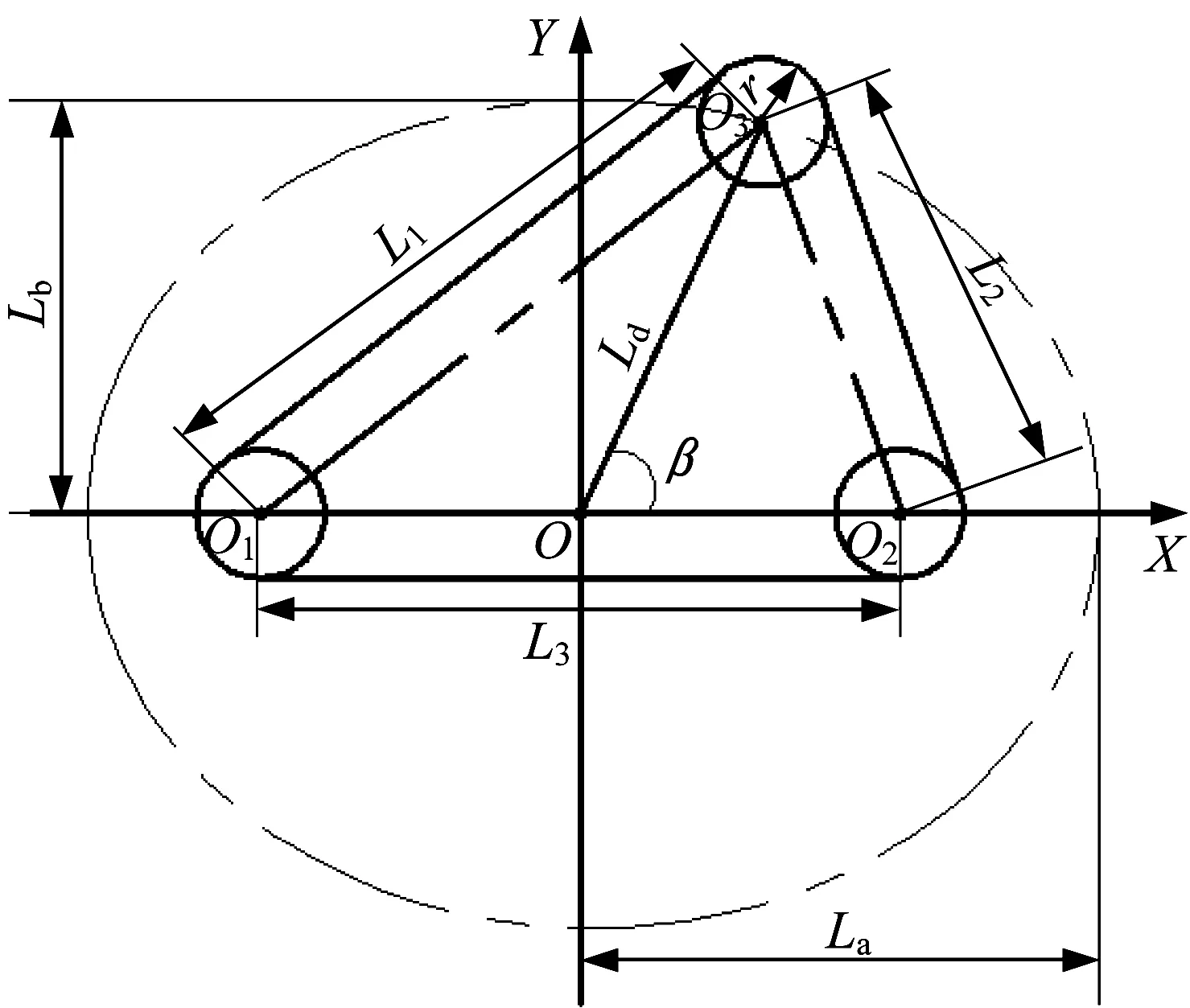
▲圖1 后擺臂構形原理

主動輪圓心O1和被動輪圓心O2相當于橢圓的兩個焦點,后擺臂末端輪圓心O3相當于行星輪,則O3的軌跡為橢圓。假設三個輪的半徑均為r,則履帶總長度L為:

L=L1+L2+L3+2πr

(1)

由橢圓定理可得:

L1+L2=2La

(2)

即:

L=2La+L3+2πr

(3)

已知La和L3為固定量,所以L為一固定值,即履帶長度只與后擺臂軌跡有關,而與機器人形狀處于何種狀態無關。

伺服電機驅動后擺臂旋轉,旋轉停止后采集顯示器上伺服電機的旋轉圈數。設后擺臂與車體鉸點為原點,后擺臂從X軸正半軸開始旋轉,每一個擺臂角度對應一個電機旋轉圈數,并且兩者為線性關系。設電機旋轉圈數為z,則后擺臂轉角β為:

β=kz

(4)

式中:k為修正因數。

后擺臂構形簡化原理如圖2所示。

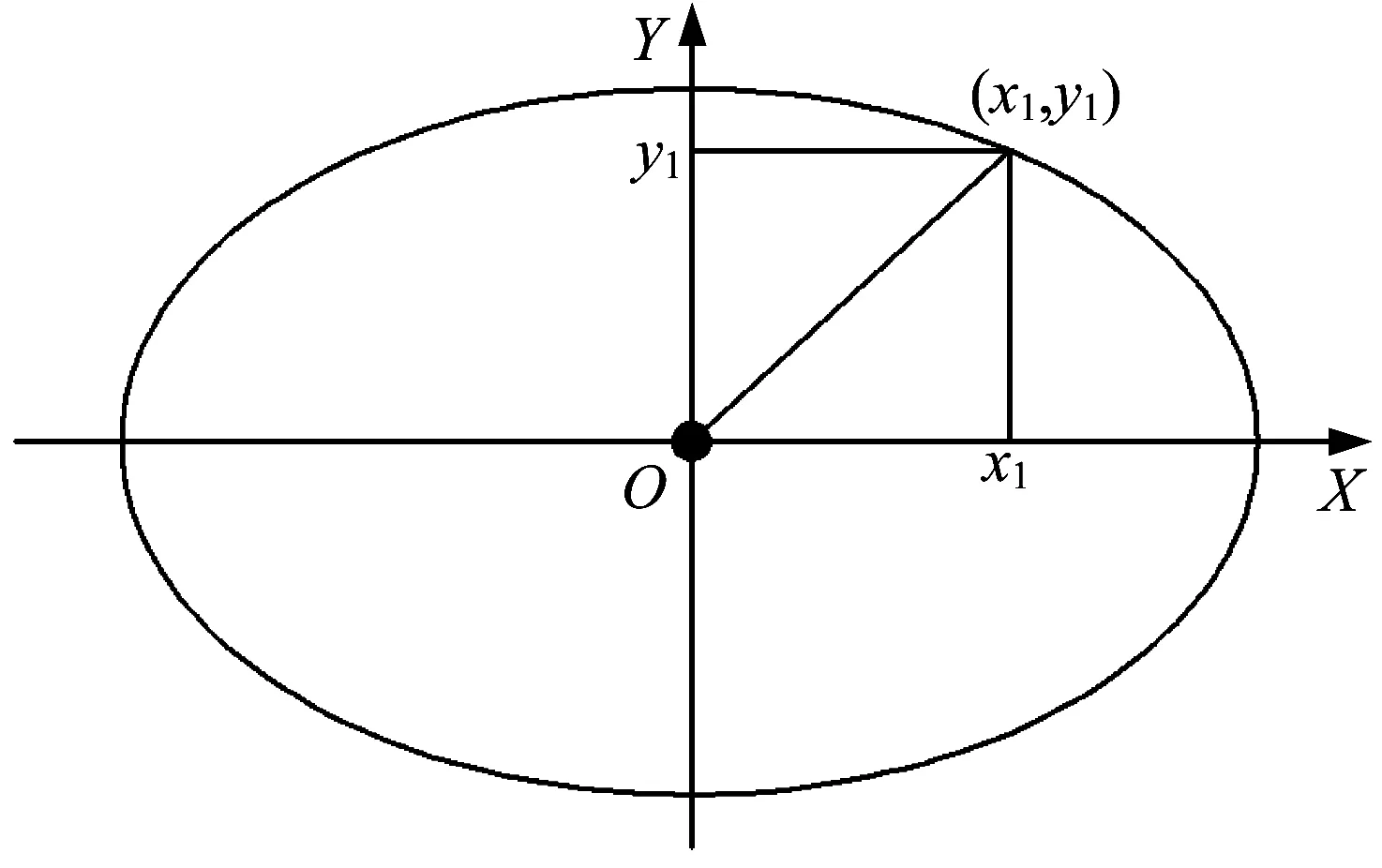
▲圖2 后擺臂構形簡化原理

在橢圓上任取一點(x1,y1),代入橢圓方程,得:

(5)

式中:a為橢圓長半軸,a=La;b為橢圓短半軸,b=Lb。

又有:

y1=x1tanβ

(6)

于是得到任意一點橫坐標x1與后擺臂轉角β的關系為:

(7)

代入式(6),得到任意一點縱坐標y1與后擺臂轉角β的關系為:

(8)

后擺臂長度Ld為:

(9)

由此可見,每一個后擺臂旋轉角度對應一個活塞桿位移。通過擺臂的驅動電機獲取擺臂的旋轉角度,數據傳輸到可編程序控制系統加以運算,可以得到對應的數字脈沖,控制液壓伺服電機使活塞桿達到對應的位移量[3]。

3 結構設計

應用SolidWorks軟件構建行走機構三維模型,如圖3所示。前擺臂水平放置,后擺臂可實現360°旋轉,兩個行星輪分別位于兩個后擺臂的末端。根據越障高度,可以實時調整后擺臂的角度。兩個后擺臂均獨立驅動。后擺臂結構如圖4所示。

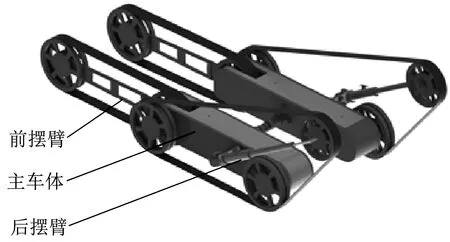
▲圖3 行走機構三維模型

所設計的液壓擺臂履帶可變形機器人參數見表1。為節省空間,減輕行走機構的質量,齒輪泵選用尺寸較小的S-10型微型齒輪泵。

4 越障過程步態規劃

機器人越障面臨復雜地形[4],由此對應豐富的結構特征,這些結構特征由點、線、面組成。對結構特征進行分類,可以歸結為臺階、凸臺、溝壑、坡道、盆地等一種或多種地形的隨機組合。

▲圖4 后擺臂結構

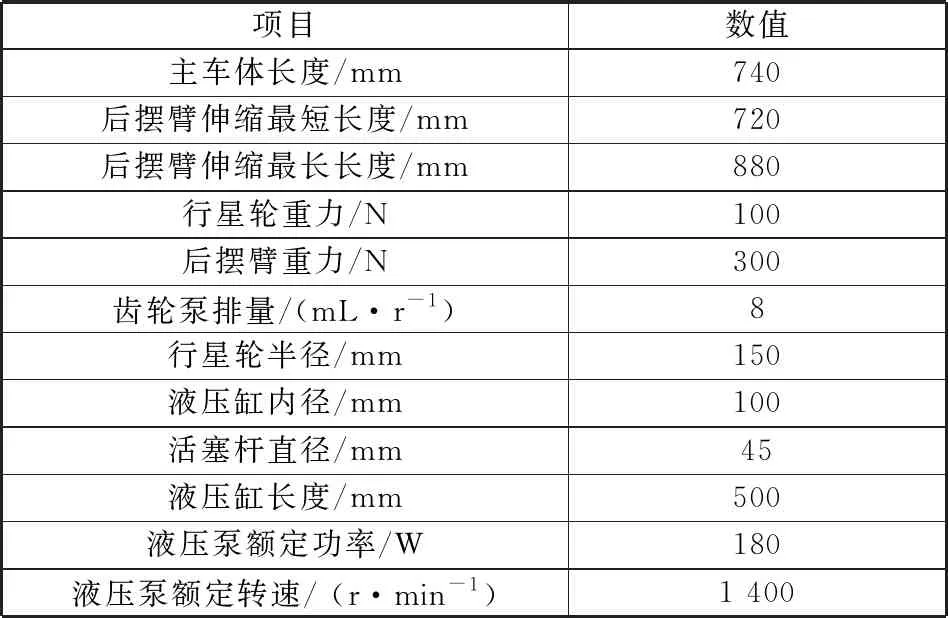
表1 液壓擺臂履帶可變形機器人參數

對液壓擺臂履帶可變形機器人翻越典型地形的過程進行動作分解[5],選取后擺臂活塞桿頂端,即行星輪中心作為關鍵點,對每一關鍵步態的關鍵點進行受力分析,以求得活塞桿所需提供的最大推力。假設液壓擺臂履帶可變形機器人行走時以勻速直線運動完成越障,即加速度為零。

4.1 爬越凸臺

液壓擺臂履帶可變形機器人爬越凸臺過程,關鍵步態分為四步。

(1) 后擺臂抬起45°,如圖5所示。此時關鍵點上的受力有行星輪重力G、擺臂抬高的驅動力F2、活塞桿推力F1,受力平衡方程為:

Gsin 45°=F1

(10)

Gcos 45°=F2

(11)

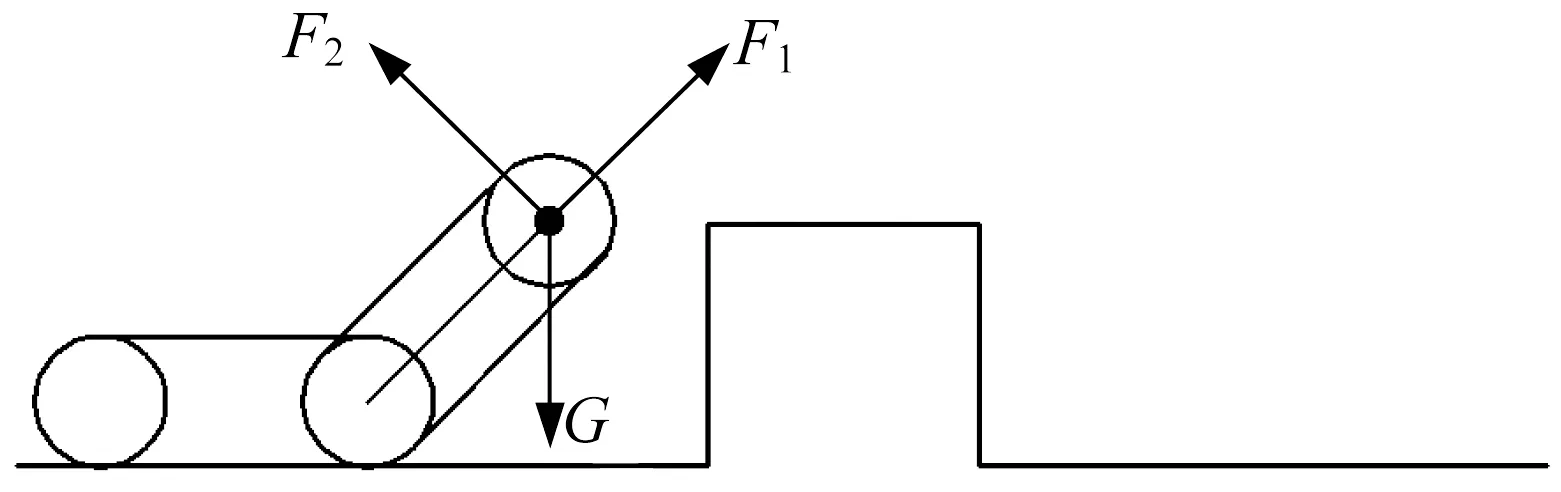
▲圖5 后擺臂抬起45°

行星輪重力G為100 N,計算得到活塞桿所需提供的推力F1為70 N。

(2) 主車體靠近凸臺,后擺臂搭在凸臺外角線上,如圖6所示。此時關鍵點上的受力有行星輪重力G、凸臺外角線對行星輪的支持力FN、活塞桿推力F1,受力平衡方程為:

Gsin 45°=FN

(12)

Gcos 45°=F1

(13)

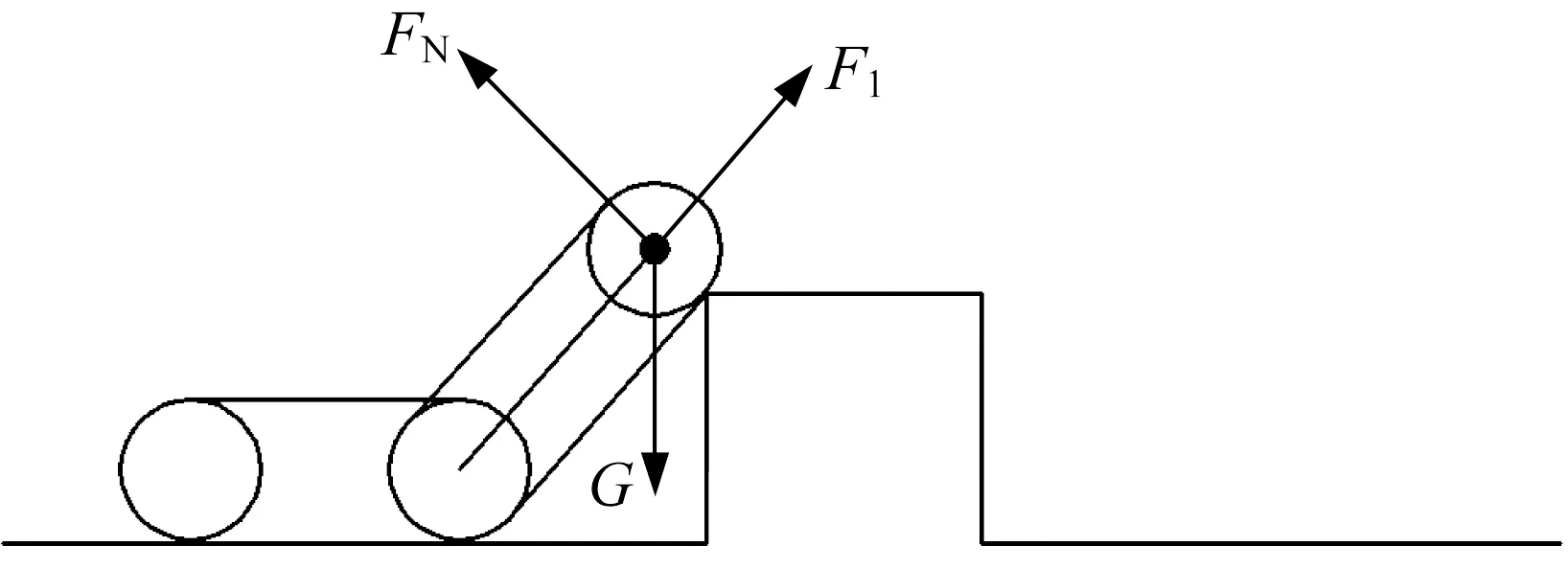
▲圖6 后擺臂搭上凸臺外角線上

行星輪重力G為100 N,計算得到活塞桿所需提供的推力F1為70 N。

(3) 后擺臂完全越過凸臺外角,在凸臺上平面行走,主車體呈45°趨勢翻越,如圖7所示。此時關鍵點上的受力有行星輪重力G、凸臺上平面對行星輪的支持力FN、活塞桿推力F1、行星輪所受摩擦力Ff,受力平衡方程為:

FN=G

(14)

Ff=F1

(15)

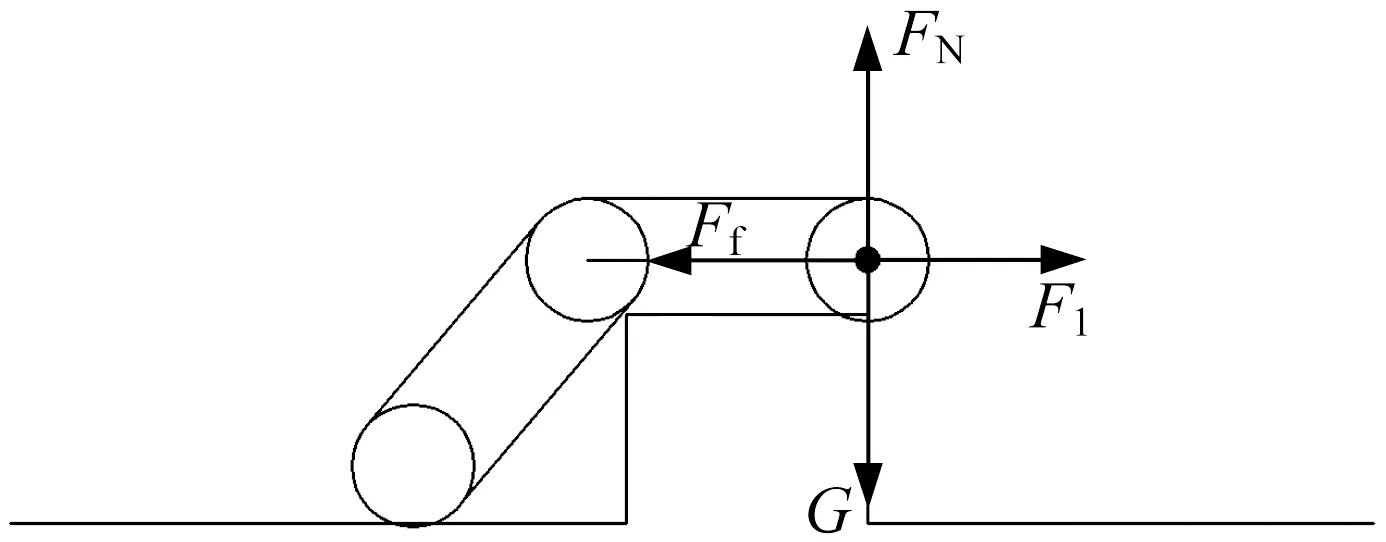
▲圖7 后擺臂越過凸臺外角

行星輪重力G為100 N,摩擦因數取0.2,計算得到摩擦力Ff為20 N,即活塞桿所需提供的推力F1為20 N。

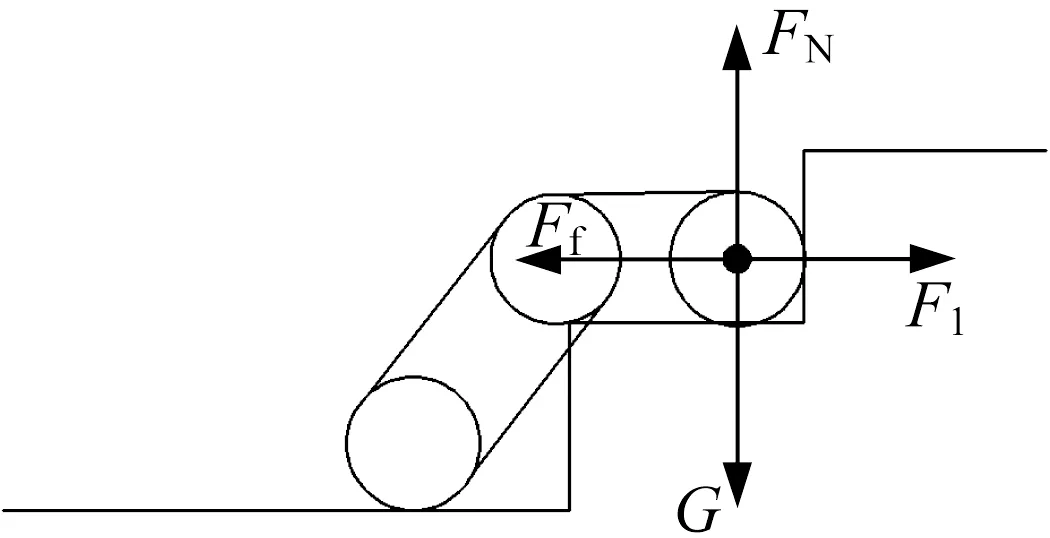
(4) 后擺臂呈45°搭在下平面上,主車體在凸臺上平面行走,如圖8所示。此時關鍵點承受的重力并非只是行星輪的重力,還包含一部分后擺臂的重力。對后擺臂做受力分析,后擺臂的主要受力有凸臺立面對后擺臂水平向右的支持力F′N、后擺臂重力G′、凸臺下平面對行星輪的支持力FN、凸臺下平面對后擺臂的支持力F″N、凸臺下平面對后擺臂的摩擦力F′f,受力平衡方程為:

F″N=G′

(16)

F′f=F′N

(17)

后擺臂重力G′為300 N,摩擦因數取為0.2,可得摩擦力F′f為60 N。再對關鍵點進行受力分析,關鍵點一共受到四個力:凸臺下平面對行星輪的支持力FN、行星輪重力G、凸臺下平面對行星輪的摩擦力Ff、活塞桿對關鍵點的推力F1。假設后擺臂與凸臺下平面的夾角為45°,則受力平衡方程為:

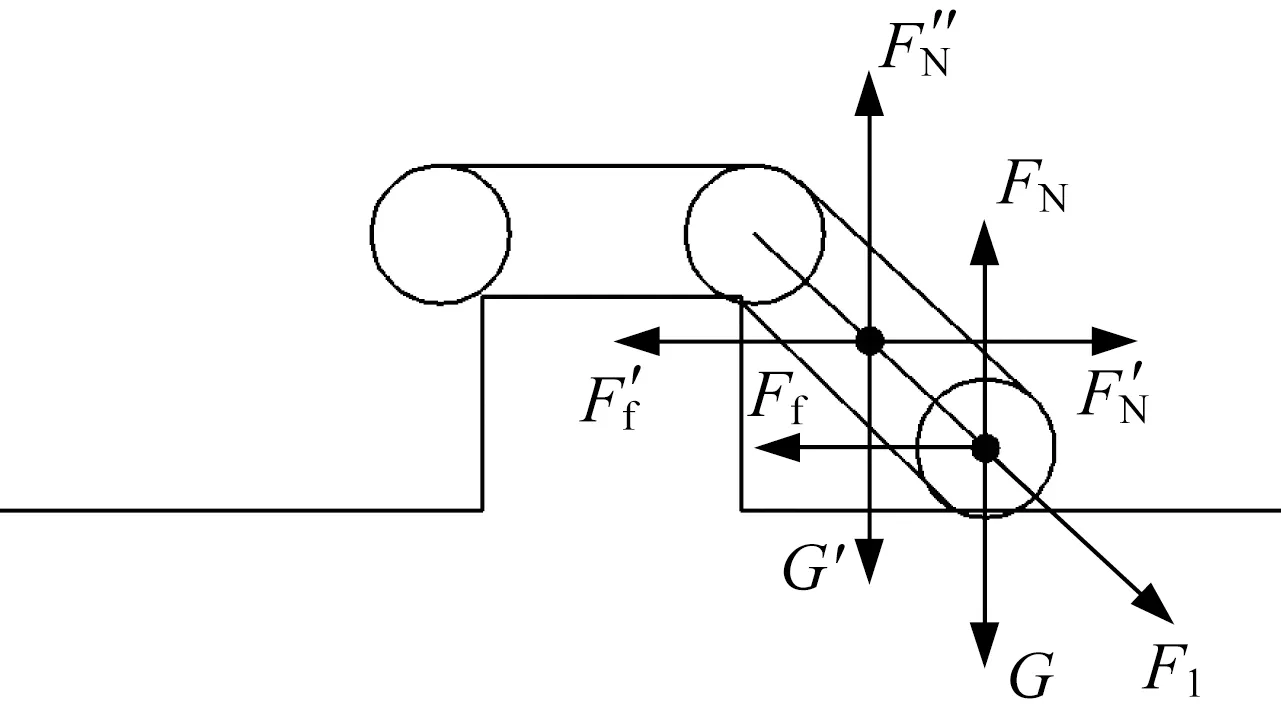
▲圖8 后擺臂呈45°搭在下平面

FN=G+F1sin 45°

(18)

Ff=F1cos 45°

(19)

計算得到活塞桿所需提供的推力F1為84 N。

4.2 爬越坡道

液壓擺臂履帶可變形機器人跨越坡道過程分為兩步關鍵步態[7]。

(1) 后擺臂抬起搭到45°坡面上,主車體仍在坡道下平面,如圖9所示。這一步態與爬越凸臺第(2)步態基本相同,活塞桿所需提供的推力F1為70 N。

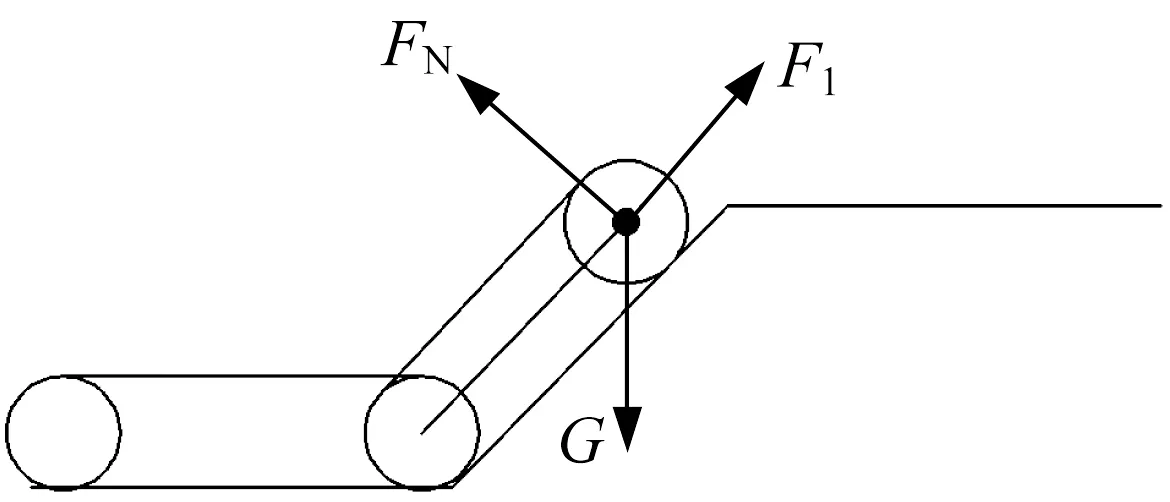
▲圖9 后擺臂搭到坡面

(2) 后擺臂在坡道上平面水平行走,主車體處于坡面上,如圖10所示。這一步態與爬越凸臺第(3)步態基本相同,活塞桿所需提供的推力F1為20 N。

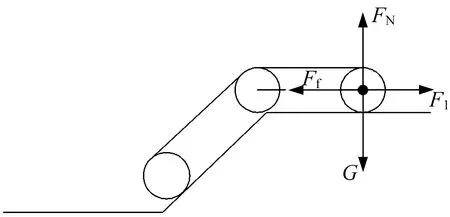
▲圖10 后擺臂在坡道上平面

4.3 跨越溝壑

液壓擺臂履帶可變形機器人跨越溝壑過程分為四步關鍵步態[8]。

(1) 后擺臂落下搭在溝壑下平面上,主車體仍在溝壑上平面水平行走,如圖11所示。后擺臂與溝壑下平面的夾角為45°,這一步態與爬越凸臺第(4)步態基本相同,活塞桿所需提供的推力F1為84 N。

(2) 主車體完全處于溝壑下平面,后擺臂呈45°抬起,如圖12所示。這一步態與爬越凸臺第(1)步態基本相同,活塞桿所需提供的推力F1為70 N。

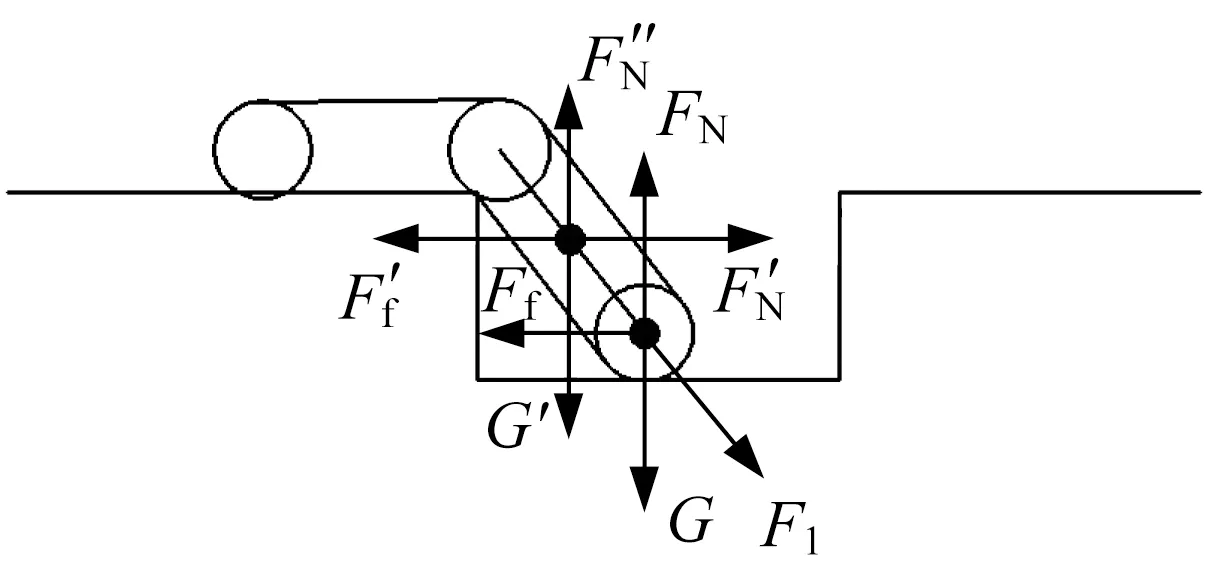
▲圖11 后擺臂搭車溝壑下平臺

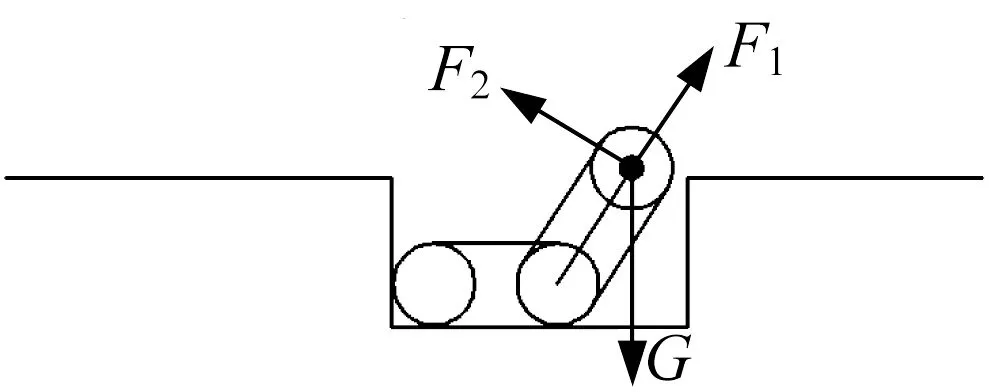
▲圖12 主車體處于溝壑下平面

(3) 主車體仍處于溝壑下平面,后擺臂搭在溝壑外角線上,如圖13所示。這一步態與爬越凸臺第(2)步態基本相同,活塞桿所需提供的推力F1為70 N。

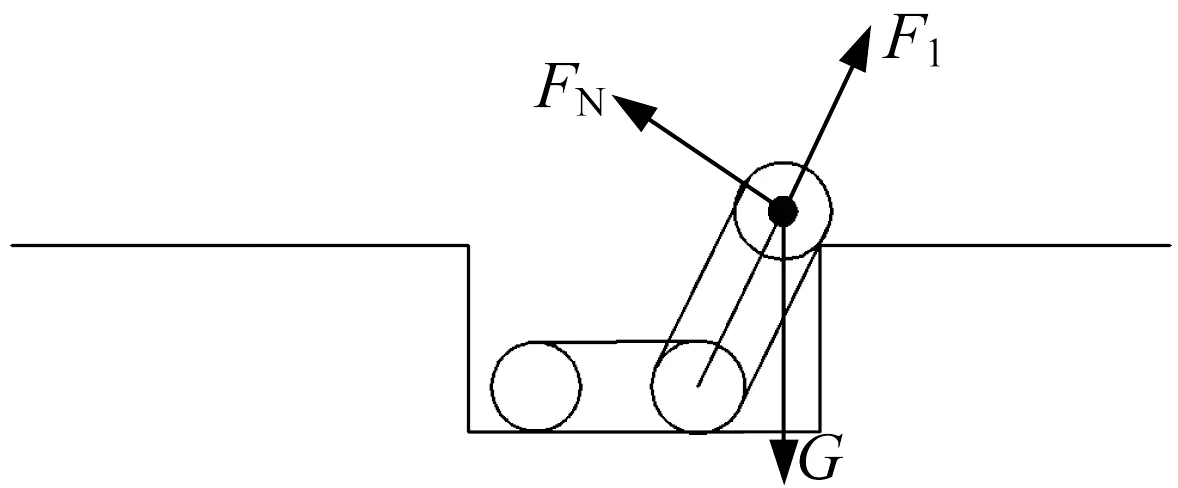
▲圖13 后擺臂搭在溝壑外角線上

(4) 后擺臂完全爬上溝壑上平面,主車體呈45°爬越狀態,如圖14所示。這一步態與爬越凸臺第(3)步態基本相同,活塞桿所需提供的推力F1為20 N。

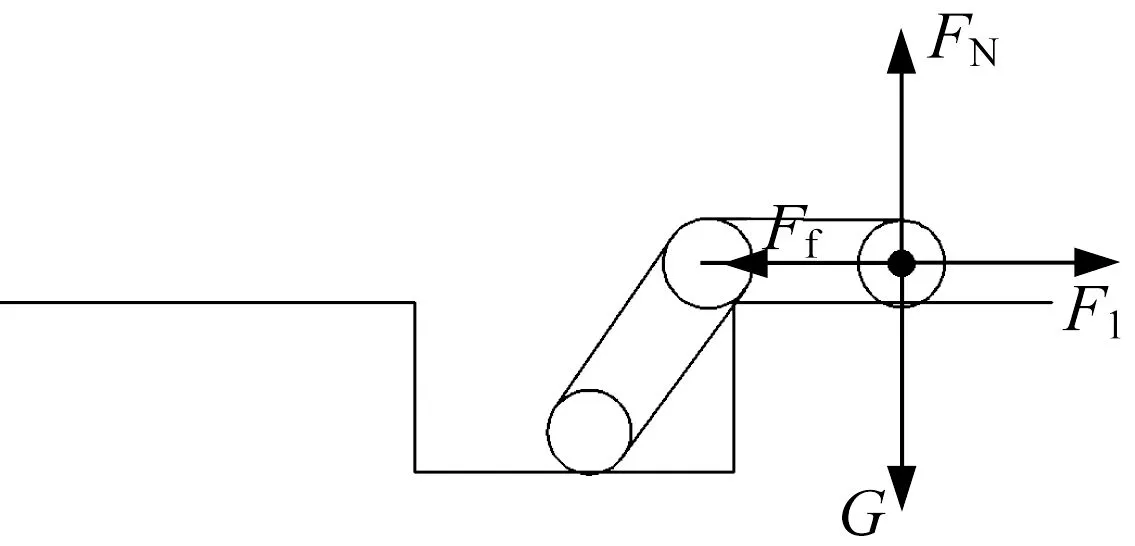
▲圖14 后擺臂爬上溝壑上平臺

4.4 爬越臺階

液壓擺臂履帶可變形機器人爬越臺階過程分為三步關鍵步態[9]。

(1) 后擺臂抬起45°,主車體在臺階下平面水平行走,如圖15所示。這一步態與爬越凸臺第(1)步態基本相同,活塞桿所需提供的推力F1為70 N。

(2) 后擺臂搭在臺階外角線上,主車體仍在臺階下平面,如圖16所示。這一步態與爬越凸臺第(2)步態基本相同,活塞桿所需提供的推力F1為70 N。

(3) 后擺臂完全爬越一級臺階,水平搭在一級臺階的上平面,主車體呈45°爬越狀態,如圖17所示。這一步態與爬越凸臺第(3)步態基本相同,活塞桿所需提供的推力F1為20 N。

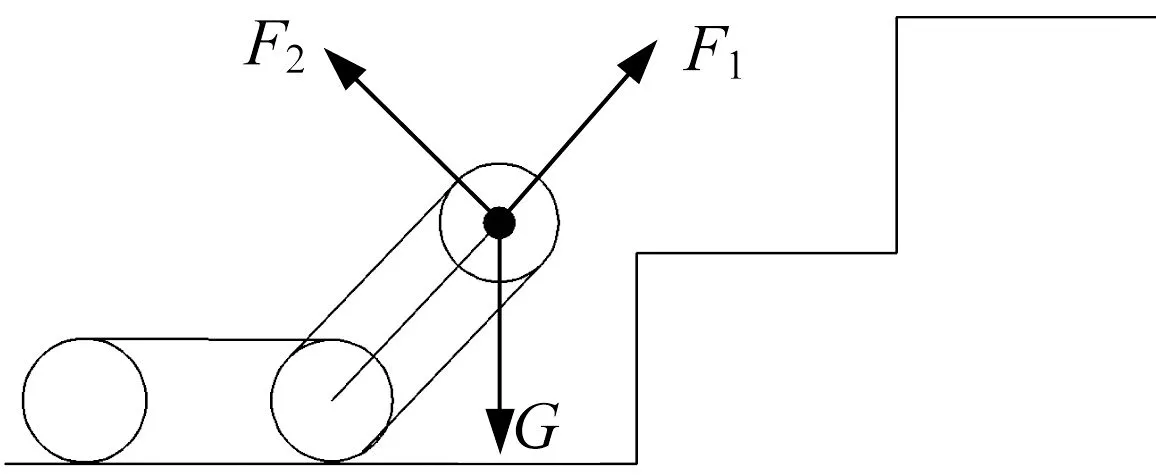
▲圖15 主車體在臺階下平面水平行走

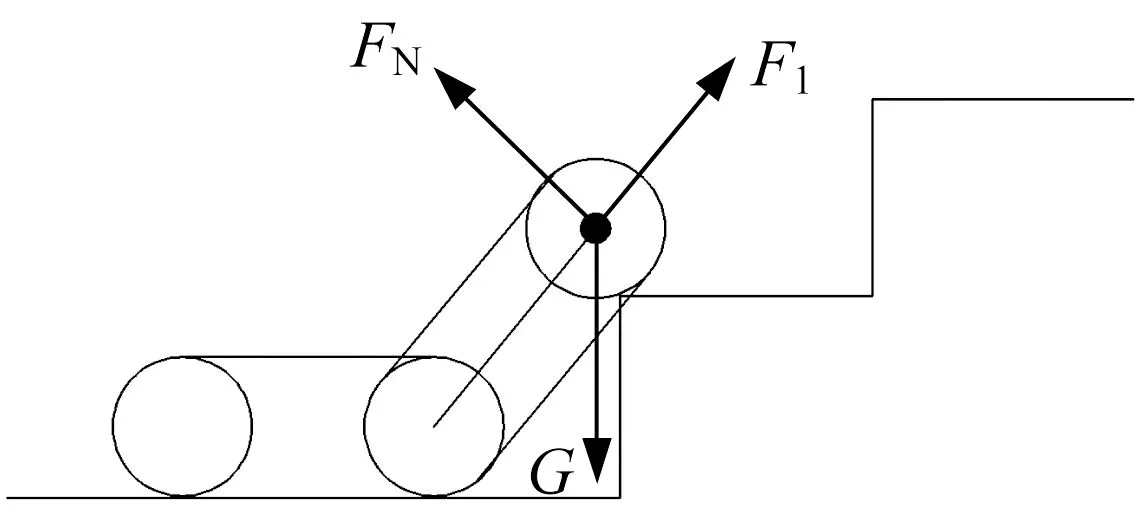
▲圖16 后擺臂搭在臺階外角線上

▲圖17 后擺臂水平搭在一級臺階上平面

4.5 跨越盆地

液壓擺臂履帶可變形機器人跨越盆地過程分為五步關鍵步態[10]。

(1) 后擺臂搭在盆地曲面上,主車體仍在曲面左上平面水平行走,如圖18所示。后擺臂與盆地左上平面的夾角為135°,這一步態與跨越凸臺第(4)步態基本相同,活塞桿所需提供的推力F1為84 N。

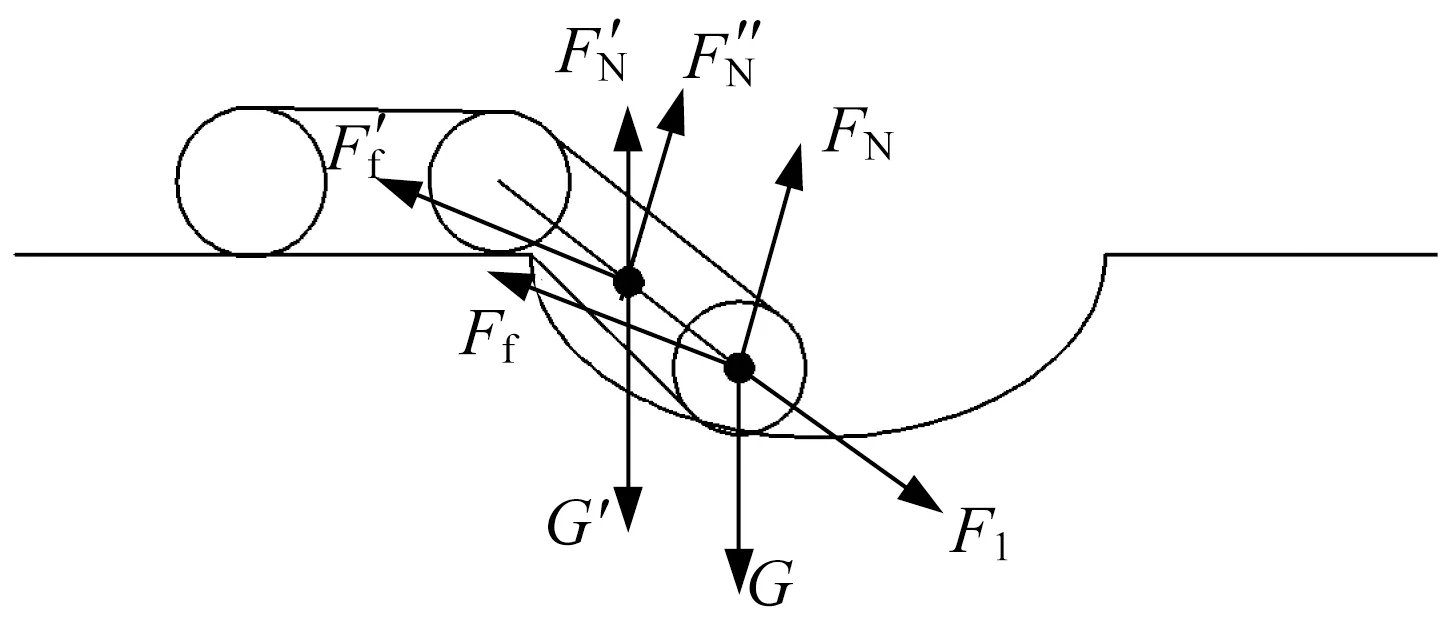
▲圖18 后擺臂搭在盆地曲面上

(2) 主車體和后擺臂完全處于盆地曲面中,如圖19所示。此時關鍵點上的受力由行星輪重力G、活塞桿推力F1、曲面摩擦力Ff、曲面對行星輪的支持力FN組成。主車體和后擺臂與盆地水平面的夾角都為30°,摩擦因數μ為0.2,受力平衡方程為:

μFN+G=F1sin 30°

(20)

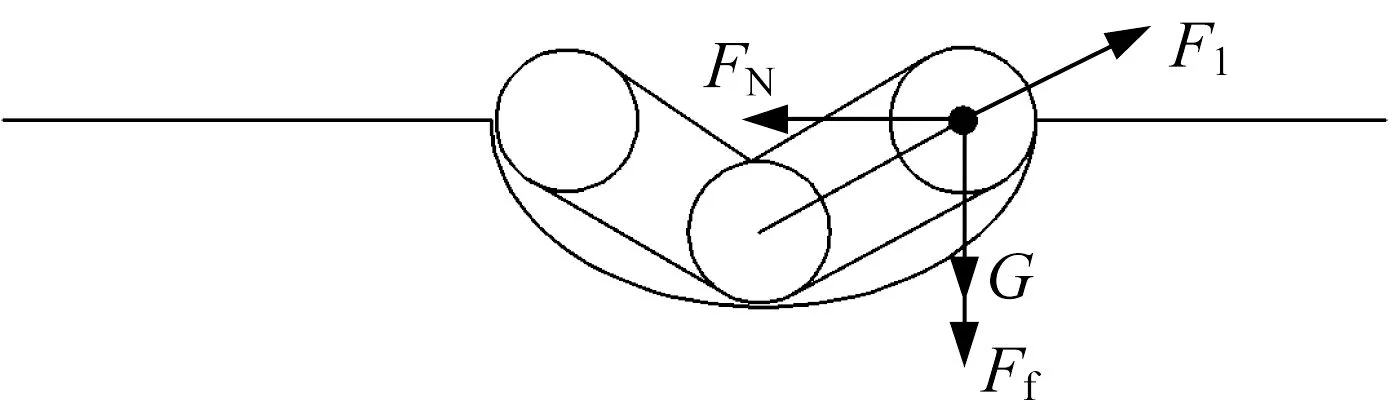
▲圖19 主車體和后擺臂處于盆地曲面中

FN=F1cos 30°

(21)

計算得到支持力FN為265.5 N,活塞桿所需提供的推力F1為306.6 N。

(3) 后擺臂抬起45°,如圖20所示。這一步態與爬越凸臺第(1)步態基本相同,活塞桿所需提供的推力F1為70 N。

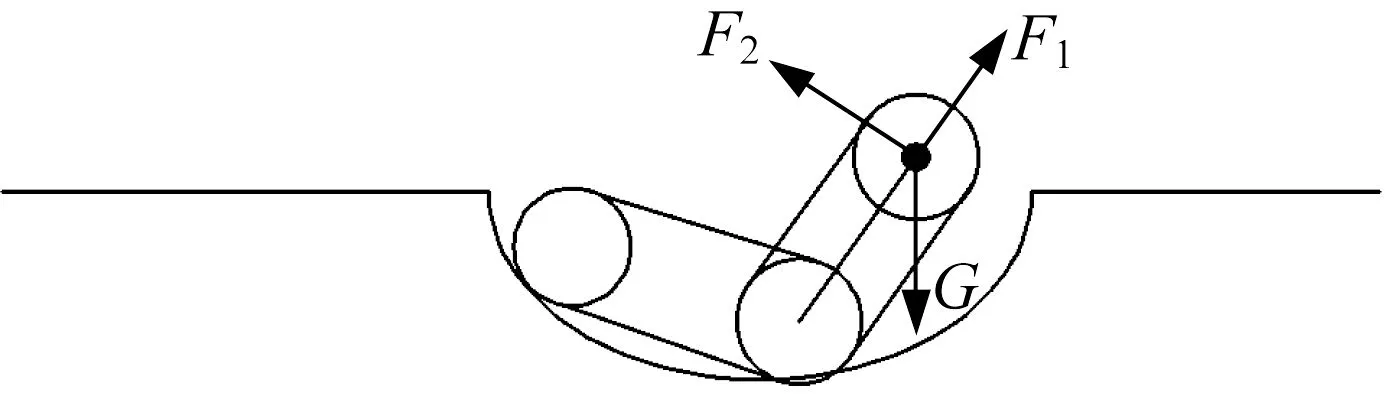
▲圖20 盆地中后擺臂抬起45°

(4) 后擺臂呈45°搭在盆地右上平面與曲面的交線上,如圖21所示。這一步態與爬越凸臺第(2)步態基本相同,活塞桿所需提供的推力F1為70 N。

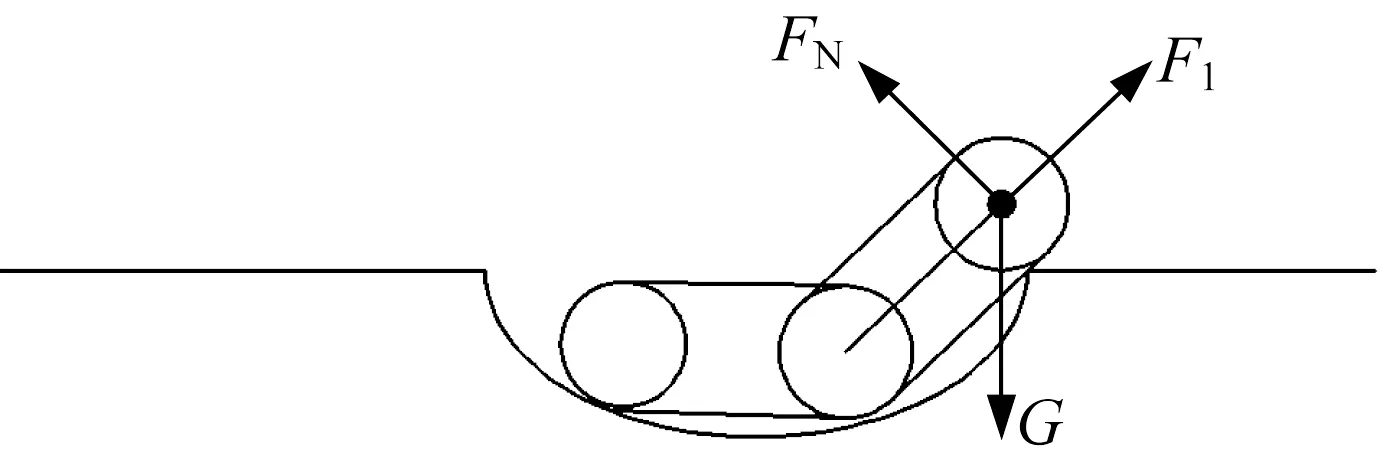
▲圖21 后擺臂搭在盆地上平面與曲面交線上

(5) 后擺臂完全水平搭在盆地右上平面上,主車體仍在盆地中,如圖22所示。主車體呈45°跨越狀態,這一步態與爬越凸臺第(3)步態基本相同,活塞桿所需提供的推力F1為20 N。

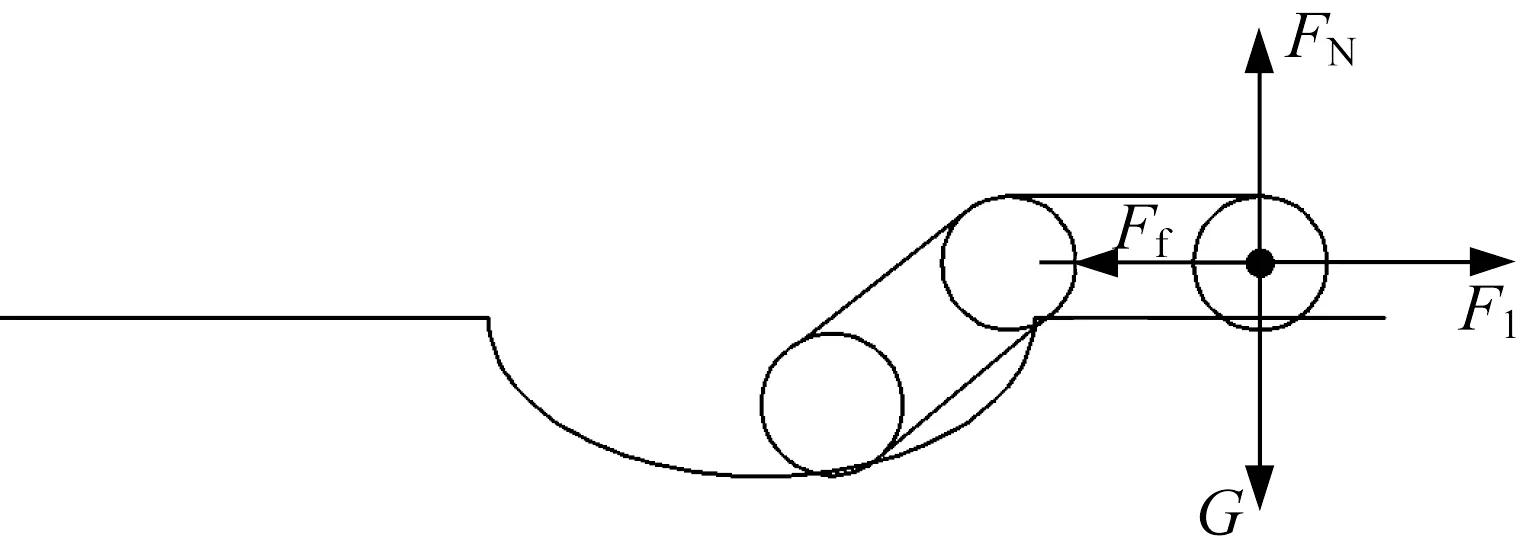
▲圖22 后擺臂水平搭在盆地上平面

對所求得的各種典型地形活塞桿所需提供的推力進行比較,液壓擺臂履帶可變形機器人后擺臂完成越障,活塞桿所需提供的推力最大為306.6 N。

5 擺臂液壓系統計算

齒輪泵流量q為:

q=Vnφv/1 000

(22)

式中:V為齒輪泵排量;n為電機額定轉速;φv為容積效率,一般取0.93。

計算得到齒輪泵流量為10 L/min。

液壓泵工作壓力p為:

p=60P/(qφ1)

(23)

式中：P為液壓泵額定功率;φ1為壓力損失總效率,一般取0.79。

計算得到液壓泵工作壓力為1.37 MPa。

液壓缸工作壓力p1為:

p1=p/K1

(24)

式中:K1為系統壓力損失因數,一般取1.5。

計算得到液壓缸工作壓力為0.91 MPa。

活塞桿額定推力F7為:

F7=p1απD2/4

(25)

式中:D為液壓缸內徑;α為負荷率,一般取0.8。

計算得到活塞桿額定推力為5 715 N。

活塞桿額定拉力F8為:

F8=p1απ(D2/4-d2/4)

(26)

式中:d為活塞桿直徑。

計算得到活塞桿額定拉力為4 558 N。

計算得到的活塞桿額定推拉力遠遠大于液壓擺臂履帶可變形機器人跨越各種典型地形時活塞桿實際所需提供的最大推力306.6 N,設計的液壓擺臂履帶可變形機器人行走機構驅動系統滿足要求。

6 結束語

筆者設計了液壓擺臂履帶可變形機器人。針對機器人行駛過程中履帶不能持續張緊的問題,將機器人行走機構的后擺臂設計為由小型液壓系統結合可編程序控制系統控制代替凸輪及橫縱軸雙導軌[11]。同時結合橢圓定理,對機器人進行了結構設計。

建立多種典型地形的數學模型,對液壓擺臂履帶可變形機器人的越障過程進行步態規劃,對關鍵點進行受力分析,驗證行走機構的越障性能。

所做設計為機器人履帶式行走機構中履帶的持續張緊問題提供了新解決思路,為后擺臂性能的研究提供了參考。