基于圓周拉普拉斯算法的機械零件邊緣檢測方法研究*

戴喬森，何毅斌，陳宇晨，劉 湘，賀蘇遜，吳琳慧，杜 偉，汪 強

(武漢工程大學 機電工程學院，湖北 武漢 430073)

0 引 言

在現代機械制造業中，機械零件是否符合生產要求離不開零件尺寸的精度檢測[1]。而測量機械零件的尺寸首先就要得到其清晰、完整的邊緣輪廓，而通過計算機視覺的方式獲得零件邊緣是近幾年研究的重點。

相較于傳統的測量方法，計算機視覺擁有速度快、精度高、不易受到人為因素影響的優勢，并逐漸被各大機械相關研究機構所采用。

邊緣檢測算法有很多，根據計算邊緣導函數類型的不同，可以將邊緣檢測算法分為一階導函數和二階導函數兩類[2]。通常情況下，一階導函數對邊緣定位速度快且節約檢測時間；二階導函數相對復雜但效果更好[3]。拉普拉斯算法以二階微分算法為基礎，因其各項同性的特點，即將圖像旋轉后濾波與先對圖像濾波再旋轉結果相同而得到更廣泛的應用。對于圖像邊緣的基本特征識別，由于采集到的原始圖像質量會受到環境因素、物體表面等不可控因素的影響[4]，在實際處理時需要人為消除不利因素對圖像的影響。

國內外學者對于應用拉普拉斯算法提高邊緣檢測的精度和效率做了許多研究和改進：文獻[5]在傳統拉普拉斯的基礎上添加了變量sigma用于確定兩個方向上的高斯核以增強圖像邊緣輪廓的清晰度，但計算時間長，導致邊緣線條較為粗糙；文獻[6]提出了改進的log算子與ViBe算法相結合的陰影消除算法，從而提高了陰影消除方法的綜合性能和魯棒性，但算法過于繁瑣，并不具備高效性的特點；文獻[7]提出了基于數學形態學的齒輪邊緣提取方法，但是經過具體實驗可知該方法不具備普遍性。

筆者提出一種圓周拉普拉斯算法，目的是在保證算法高效性的同時，提高邊緣檢測的清晰度和細節的完整性，并加入數學形態學中的頂帽變換和底帽變換，以保證圖像的抗噪性。

1 拉普拉斯算法

一個二維圖像函數的拉普拉斯算法定義為:

(1)

對于離散二維圖像，可以用下式作為對二階偏微分的近似:

(2)

(3)

將上面兩式相加就得到用于圖像銳化的拉普拉斯算法:

▽2f=[f(i+1,j)+f(i-1,j)+f(i,j+1)+f(i,j-1)]-4f(i,j)

(4)

這個公式可以由以下濾波模板來實現:

分析拉普拉斯算法模板的結構可知，這種模板對于90°的旋轉是各向同性的。更進一步，還可以得到如下對于45°旋轉各向同性的拉普拉斯算法模板[8]:

2 圓周拉普拉斯邊緣檢測算法

2.1 圓周拉普拉斯算法

筆者在1節中對傳統的拉普拉斯算法模板生成原理進行了分析，接下來將在此基礎上對其進行改進。

圖像I在經過旋轉、平移、縮放后，可得到圖像I′，即：

I′=k·S·I+β

(5)

式中：k—圖像縮放的比例，是標量；S—旋轉矩陣；β—圖像偏移量。

變換后圖像上各點坐標對應關系為：

(6)

求一階導數可得：

(7)

式中：Iu—圖像在u方向的偏導數；Iv—圖像在v方向的偏導數。

將矩陣窗函數變成一維向量，變換后的公式如下所示：

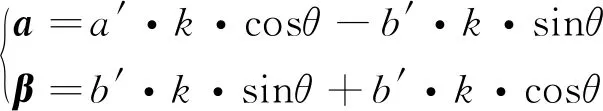
(8)

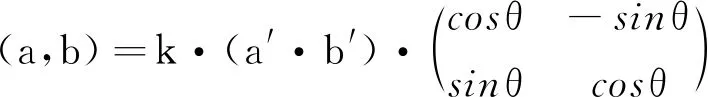
(9)

式中：M—原圖像的相關矩陣；a—Iu加權后的一維向量；b—Iv加權后的一維向量；a′，b′—變換后的a，b向量。

原圖像的相關矩陣為：

(10)

將式(8，9)代入式(10)中可得：

(11)

圖像變換后的灰度相關性為：

(12)

故圖像經變換后的灰度矩陣為：

(13)

當k=1時，圖像僅進行平移和旋轉，變換前后矩陣M是相似的，故平移和旋轉對判別式沒有影響；

當k≠1時，即圖像縮放，M不相似，故傳統的拉普拉斯算法不具有不變性。

傳統的拉普拉斯算法和圓周算法模板的對比如圖1所示。

圖1 傳統拉普拉斯算法模板和圓周拉普拉斯算法模板

由圖1可知：傳統的拉普拉斯算法一般選用3×3的模板進行濾波，在傳統的算法中，由于拉普拉斯算法的模板為矩形；當圖像發生旋轉時，必然會影響邊緣檢測的準確性。

本文提出圓周拉普拉斯算法模板，通過圓周上像素點來確定圖像邊緣；由于圓周上各點到中心點距離相等，當圖像發生旋轉時，圓周上的點不會發生變化，進而邊緣檢測的準確性也不會受到影響。

因此，筆者提出的圓周拉普拉斯算法模板具有旋轉不變性。

2.2 數學形態學去噪法

由于銳化算法的作用是突出圖像的細節，但并不能區分圖像中有效的邊緣和無效的噪聲，在實際應用中通常不單獨使用。由于數學形態學不僅能消除圖像的噪聲，還能做到不破壞圖像邊緣的細節[9]。

筆者算法將結合灰度級形態學中的頂帽變換和底帽變換，對已經提取到的零件邊緣進行優化。

2.2.1 灰度級形態學腐蝕

灰度級形態學腐蝕定義如下:

(14)

式中：b—非平坦結構元；f—原圖像相關矩陣。

2.2.2 灰度級形態學膨脹

灰度級形態學膨脹的定義如下:

(15)

式中：b—非平坦結構元；f—原圖像關矩陣。

2.2.3 灰度級形態學的開操作和閉操作

灰度級形態學腐蝕的定義如下：

f°b=(fΘb)⊕b

(16)

式中：b—非平坦結構元；f—原圖像關矩陣。

具體含義是先用結構元b對圖像f做腐蝕，隨后用結構元b對所得結果進行膨脹。同理，結構元b對圖像f的閉操作表示為f·b，即：

f·b=(f⊕b)Θb

(17)

式中：b—非平坦結構元；f—原圖像關矩陣。

開操作用來平滑物體的輪廓、斷開窄狹頸并消除較細的突出物。比操作用來連接窄間斷和長溝壑，消除小的孔洞，填補輪廓線中斷裂的區域。

2.2.4 灰度級形態學的頂帽變換和底帽變換

由式(14～17)可以組成繪圖形態學的top-hat(頂帽)變換和bottom-hat(底帽)變換[10,11]。灰度級圖像f的頂帽變換指的是f減去其開操作，即：

That(f)=f-(f·b)

(18)

同理，灰度級圖像f的底帽變換指的是f的閉操作減去f，即：

Bhat(f)=(f·b)-f

(19)

在圓模板拉普拉斯算法邊緣檢測圖像上，加上頂帽變換再減去底帽變換，就可以在不增加運算復雜度的情況下有效地抑制噪聲，從而提高圖像的有效信息。

3 實例分析

實驗采集到的齒輪零件圖和手表零件圖如圖2所示。

圖2 實驗零件圖

實驗中，使用了兩種傳統拉普拉斯算法和筆者提出的圓周拉普拉斯算法進行對比，其結果如圖3所示。

圖3 傳統拉普拉斯算法與拉普拉斯圓周算法的實驗效果

圖3(b，f)是使用傳統拉普拉斯算法中90°各項同性的模板對齒輪和零件圖進行銳化的實驗效果圖；

圖3(c，g)是使用傳統拉普拉斯算法中45°各項同性的模板對齒輪和零件圖進行銳化的實驗效果圖；

圖3(d，h)是使用本文提出的圓周拉普拉斯算法模板進行銳化的實驗效果圖。

對零件邊緣提取結果放大的圖如圖4所示。

圖4分別是90°各項同性模板、45°各項同性模板、圓周拉普拉斯算法模板對齒輪零件進行實驗結果的局部放大圖。

對比3種算法的實驗結果可以看出：傳統拉普拉斯算法對于提取的零件邊緣存在不連續、不清晰的缺陷，而使用圓周拉普拉斯算法提取出的零件邊緣則更加連續，細節保留地更加完整。

從圖3(d，h)可以看出：僅使用圓周拉普拉斯算法并不能去除圖像中的噪聲。因此，為了得到更符合實際生產需要的邊緣輪廓圖，還需要對圖像進行去噪。

采用數學形態學中的頂帽變換和底帽變換的結果如圖5所示。

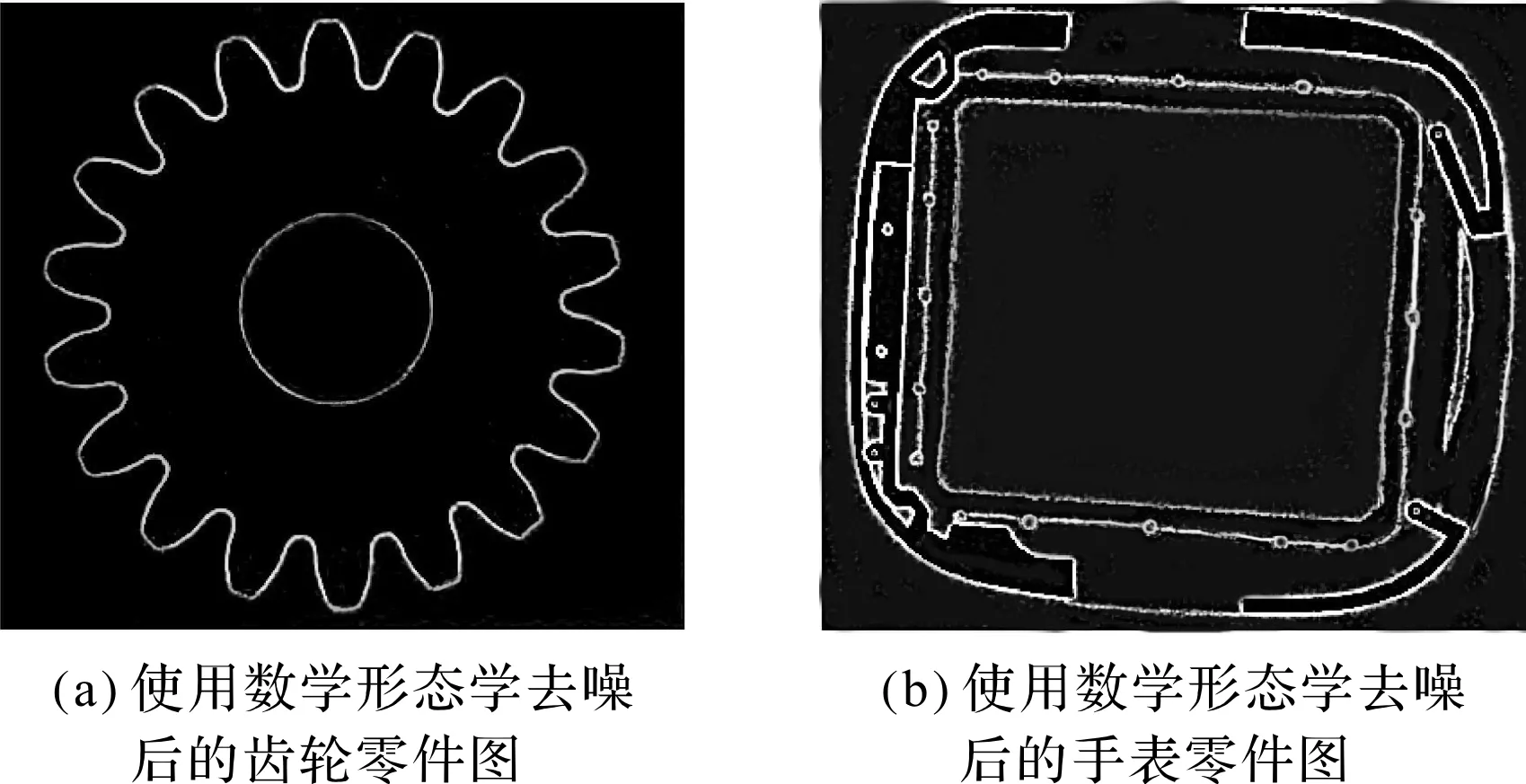
圖5 使用數學形態學去噪的效果最終效果圖

由圖5可以看出，使用數學形態學去噪后，圖像中的噪聲得到了明顯的抑制。

峰值信噪比(PSNR)作為一種評價圖像質量的檢測方法，因其普遍適用的特性而被廣泛運用在各種實驗中；且其值越大，被證明其檢測效果越好，算法越優秀。

筆者分別對齒輪零件和手表零件的3種算法的實驗過程進行了計算，其對應的峰值信噪比得到的結果如表1所示。

表1 圖像邊緣檢測效果評價表

從表1中可以看出：圓周拉普拉斯算法的峰值信噪比比傳統算法更大，說明筆者提出的算法起到了改進的作用。

從該實驗結果可以看出：

(1)傳統拉普拉斯算法在檢測機械零件邊緣上存在清晰度不足、細節失真等問題，且由于其旋轉不變性，圓周拉普拉斯算法可以有效地避免這點；運用圓周拉普拉斯算法檢測出的零件邊緣更接近真實情況；

(2)在應用圓周拉普拉斯算法邊緣檢測的機械零件圖像上，加上數學形態學的頂帽變換和底帽變換，可以在不影響圖像邊緣細節的前提下，有效地抑制噪聲。

4 結束語

通過傳統的邊緣檢測算法得到的圖像往往存在邊緣不連貫和細節缺失的問題，提取的邊緣效果不理想。

針對傳統算法的這類缺陷，筆者提出了一種圓周拉普拉斯算法，并采用了常見的齒輪和手表零件進行了實驗驗證。實驗結果證明，圓周拉普拉斯算法方法能夠完整地保留機械零件圖像中的邊緣信息，能更有效地還原圖像邊緣的有效信息；同時，加入了數學形態學中的頂帽變換和底帽變換進行去噪處理，可以去除圖像中的無效信息，得到噪聲少、邊緣曲線連續、清晰、圖像信息保留完整的零件圖像。

最后，筆者采用峰值信噪比法，對傳統算法與圓周拉普拉斯算法進行了對比，其結果證明，筆者所提出的算法更為優秀。