基于協同進化策略改進的MOEA/D 算法*
王啟翔,許 峰
(安徽理工大學 數學與大數據學院,安徽 淮南 232001)
2007年,Zhang[1]提出了基于多目標分解的MOEA/D,但是隨著目標維數的上升,全局搜索能力下降,容易陷入局部最優。為了改善MOEA/D 算法,許多學者做了大量研究、改進工作。2018年,Ryoji[2]分析了MOEA/D 的控制參數;2020年,Dong[3]提出了自適應權重 MOEA/D;Zhang[4]提出了基于信息反饋的MOEA/D;Wang[5]提出了自適應演化策略MOEA/D;Zhang[6]提出了多階段動態演化MOEA/D;Fan[7]提出了基于角度約束的MOEA/D。
2009年,張敏[8]提出了一種基于正態分布交叉的MOEA算法;2019年,Zhang[9]將差分算子引入 MOEA 算法,提出了一種雙變量控制MOEA/D 算法。本文在上述工作的基礎上,將正態分布交叉算子和差分進化算子引入MOEA/D,構成協同進化,并用標準多目標優化測驗函數對改進算法進行了性能測試,驗證了新算法的有效性。
1 MOEA/D 算法
MOEA/D 通過預先設定的權重向量將復雜的多目標優化問題轉變為一系列的單目標問題,每一個子問題使用與其相鄰的子問題提供的參考信息,相互協同進化,主要用于求解MaOP。該算法采用Tchebycheff 分解法,MOEA/D 的基本步驟如下:
(1)N:子問題的個數;
(2)N 個均勻分布的權重向量:λ1,λ2,...,λN;
(3)T:每個權重向量鄰居的個數。
步驟1 初始化:
(1)設EP=Φ。
(2)計算任意兩個權重向量之間的歐幾里德距離,為每個權重向量選出最近的T 個權向量作為它的鄰域。即 λi1,λi2,...,λiT是離 λi最近的 T 個權重向量,i=1,2,…,N,令 B(i)={i1,i2,…,iT}。
(3) 根據權重向量來產生初始種群 x1,x2,…,xN。
步驟2 更新:
對 i=1,2,…,N:
(1)從 B(i)中隨機選取兩個序號 k,l,對 xk和 xl執行SBX 算子產生一個新的解y。
(4)更新EP:剔除EP 中受y 支配所有的向量,并且在EP 中向量都不支配y 時,令EP=EP∪{f(y)}。
步驟3 終止條件:如果滿足終止條件,則停止并輸出EP,否則轉步驟2。
2 交叉算子
交叉算子是進化算法領域中最為關鍵的存在,交叉算子的優劣往往能夠決定算法的優劣。最經常用的交叉算子就是Deb 提出的模擬二進制交叉算子,其定義為:對兩個父代個體 X1和 X2,如下操作得到子代個體
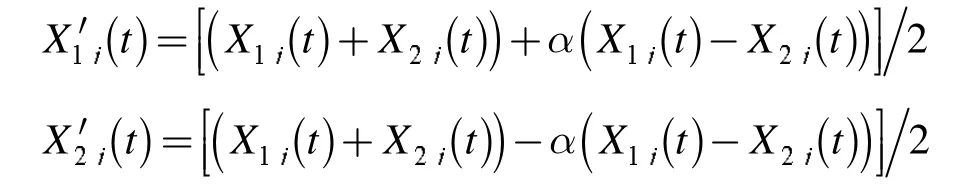
其中,j=1,2,…,n,α 是隨機變量,每一維上都要重新產生,方式如下:
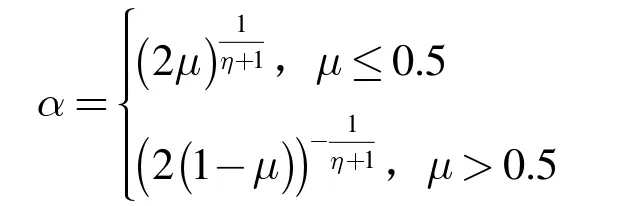
μ 是分布在(0,1)上的隨機數;η 是交叉參數。
正態分布交叉算子(NDX)是張敏[8]等在2009年提出的,就是將正態分布引入SBX 算子中,其定義為:對兩個父代個體 X1和 X2,如下操作得到子代個體
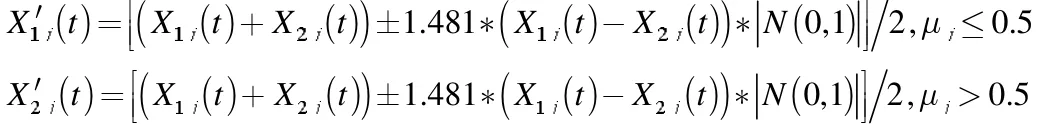
其中,μj是(0,1)區間上的隨機數。
在設計NDX 的時候,引入重組操作,增強了NDX 算子空間搜索能力。NDX 相較SBX 的優勢在于對大量的個體進行重組操作,能夠擴大種群的多樣性,提供更大的搜索范圍。
DE/best/2 引入了最優解個體引導搜索方向,變異個體的生成受到最優解個體的制約,搜索范圍將圍繞最優解展開,因而使得算法的收斂速度大大增加,趨向最優解的能力提高,然而若當前最優解個體為局部極值點,則會因為種群多樣性降低而增大陷入局部最優解的可能性。
3 協同進化策略
在多目標進化算法中,如果一個算法能有一個優秀的產生子種群的策略,那么這個算法的性能必定會大大提高。MOEA/D 利用模擬二進制交叉算子SBX 來生成子代,并且取得比較好的效果,但是該算法的搜索能力較弱,生成的種群多樣性較差,且SBX 算子易產生劣質子代等等。針對這些缺陷,本文利用NDX 正態分布交叉算子和DE/best/2 差分進化算子來構建協同進化策略,替換SBX 算子,讓NDX 算子和DE/best/2 算子共同生成子代。
首先NDX 可以對子問題鄰域內大量的個體進行重組操作,使父代個體更具多樣性,從而能夠產生多樣性的個體,擴大種群多樣性,提供更大的搜索范圍;其次,從NDX 產生的種群中,執行DE/best/2。
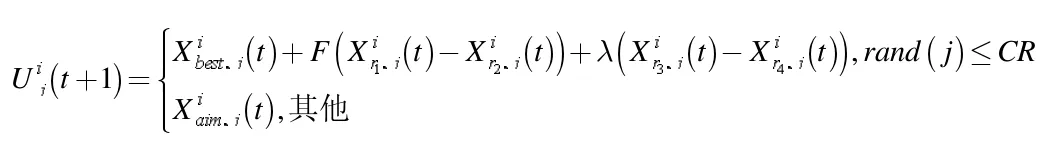
4 協同進化策略改進的MOEA/D 算法
步驟1 初始化參數。生成一組分布均勻的權向量λ1,λ2,……,λN,計算子問題鄰域 B(i)={i1,i2,…,iT},根據權向量生成一個初始隨機種群 P={x1,x2,…,xN},取每一個目標值的最小值作為參考點
步驟2 種群更新。
對 i=1,2,…,N
(1) 對 B(i)中所有個體,兩兩執行 NDX 算子,得到新的子代種群記為Q(i)。
(2) 將 B(i)和 Q(i)合并,記為 Rt。
(3)從Rt選擇合適的個體,執行DE/best/2 算子,生成新個體y。
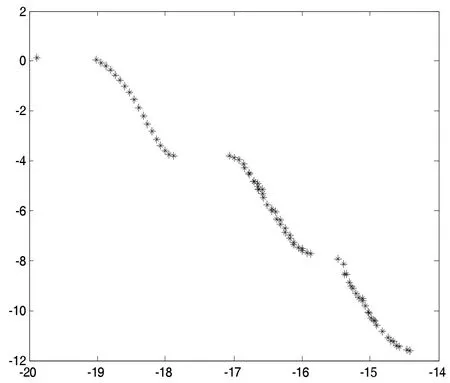
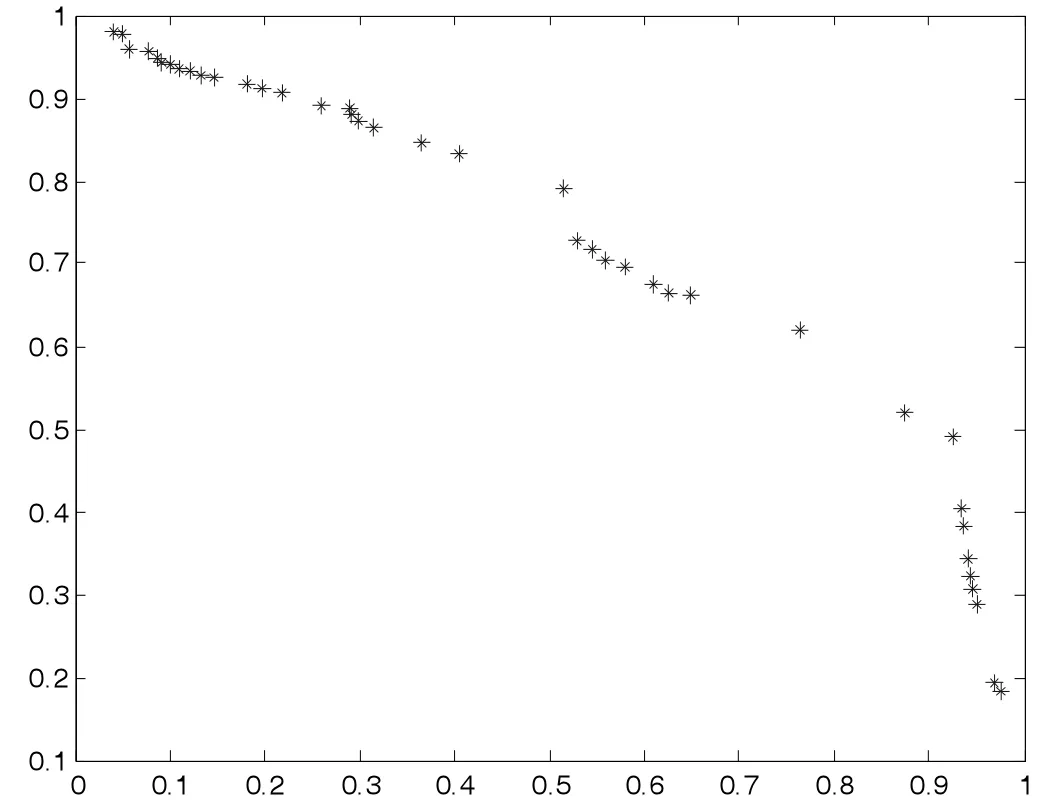
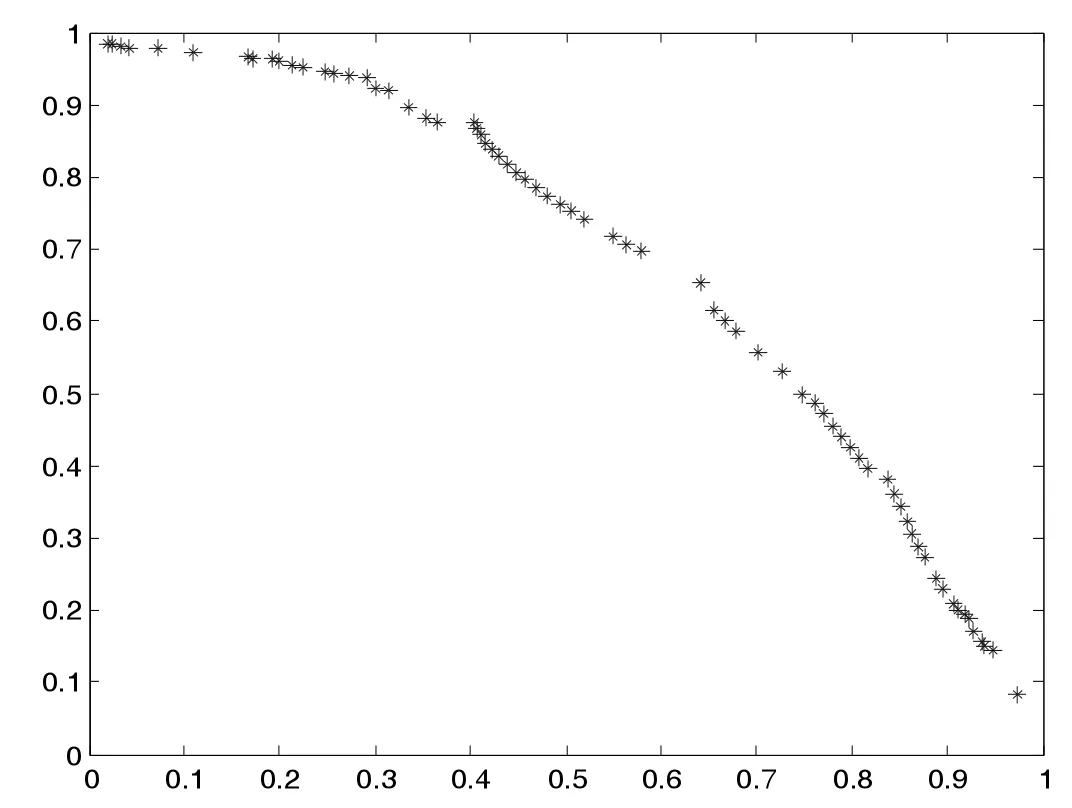
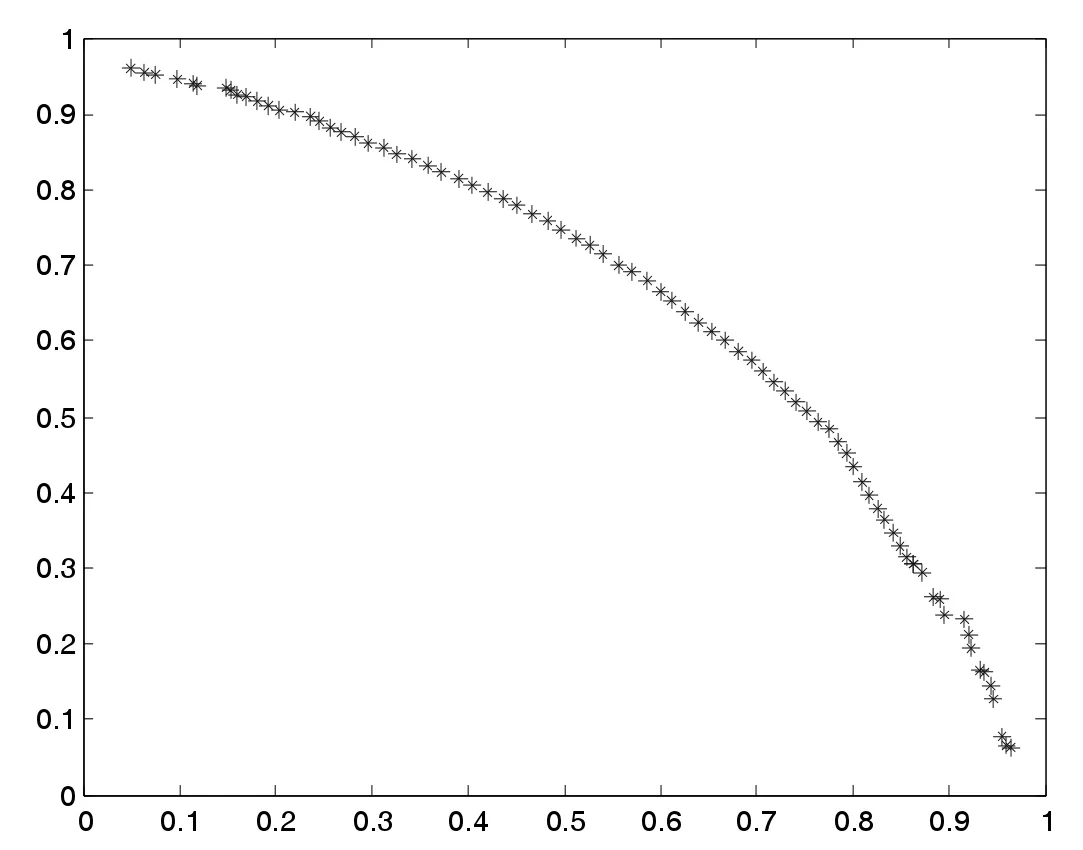
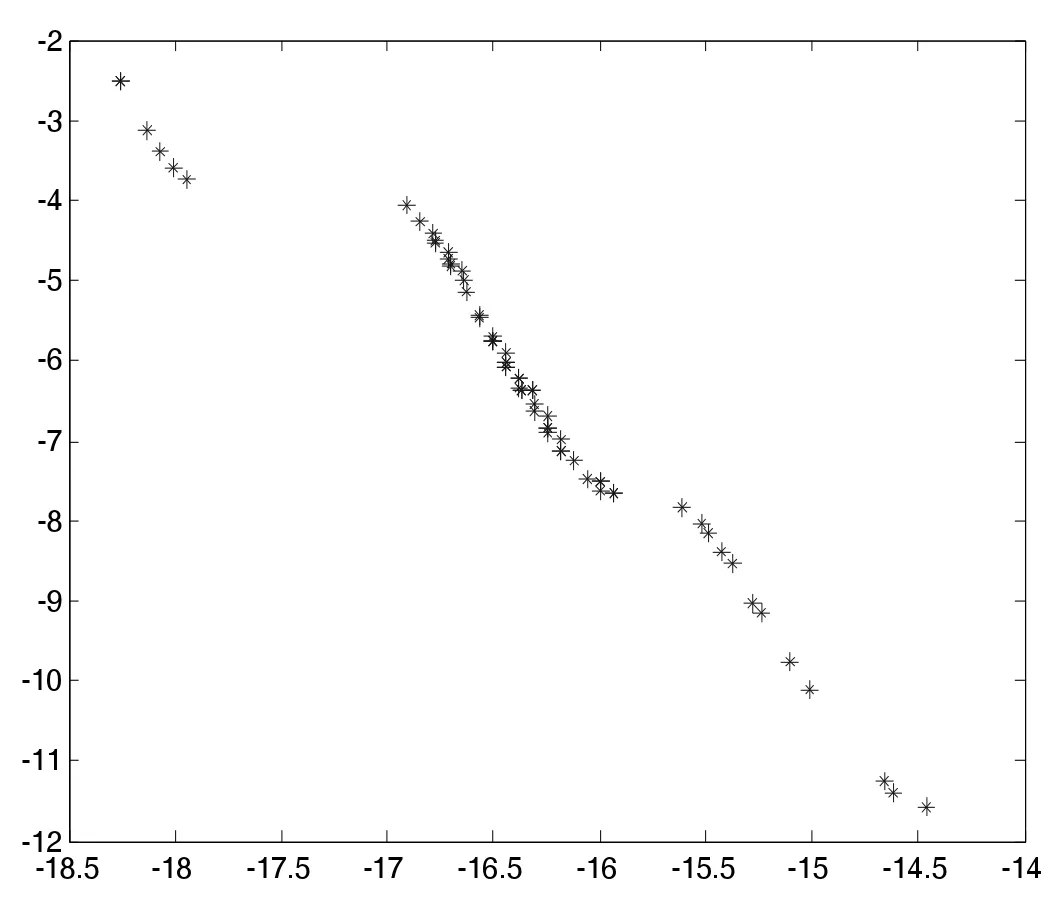
(4)若zj 步驟3 更新EP。如果新生成的解y 不被EP 中的任何解所支配,并刪除由y 主導的解。 步驟4 終止條件:如果滿足終止條件,則停止并輸出EP。否則轉到步驟2。 為了評測改進算法的收斂性和分布性,選取下面兩個標準測試函數進行數值計算: 其中,-4≤x1,x2,x3≤4。 其中,-5≤x1,x2,x3≤5。 首先進行非支配解個數的生成比例實驗,這是評測算法收斂性的一種直觀方法。下面給出了非支配解不同生成比例時F1的Pareto 最優前沿。 圖1 40%非支配個體 圖2 60%非支配個體 上述圖1-圖4 圖形顯示,對于固定的種群規模,隨著非支配解比例的增加,算法較好地逼近了理論上的Pareto 最優前沿。這在一定程度上表明,改進算法具有較好的收斂性。 下面再將改進算法與標準MOEA/D 算法進行比較。下面給出兩種算法的對比Pareto 最優前沿。 從上述圖5-圖6 圖形可以清楚地看出,改進的MOEA/D 與標準的MOEA/D 相比,有較好的分布性和均勻性。 圖3 80%非支配個體 圖4 90%非支配個體 圖5 F2MOEA/D 的Pateto 最優前沿 圖6 F2 改進MOEA/D 的Pateto 最優前沿 受以往工作的啟發,本文將正態分布交叉算子和差分進化算子引入MOEA/D,數值實驗表明,改進后的算法維持了MOEA/D 的良好收斂性,而且較MOEA/D 在分布性和均勻性方面有了一定程度的改進。不過,這不可避免地增加了算法的復雜度。5 數值實驗與性能測試
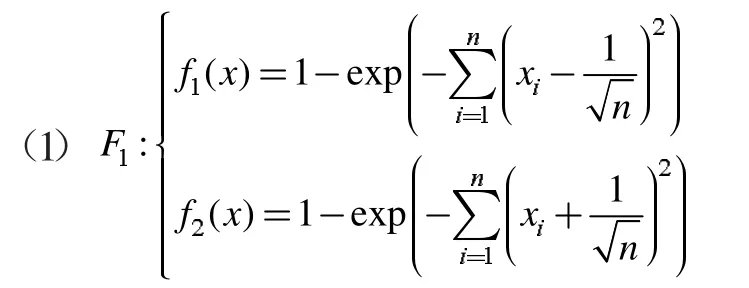
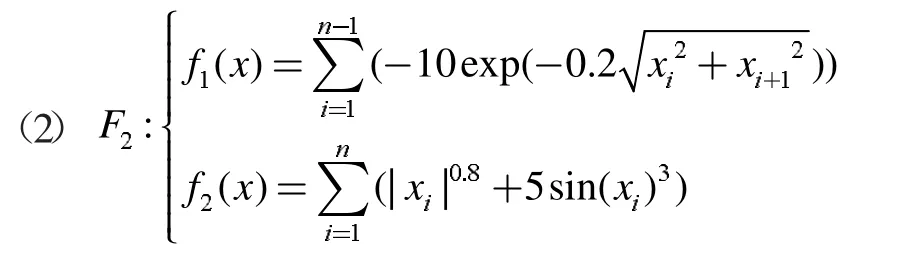

6 結論