吸盤式電磁鐵殘余吸力研究

寧劍建，章 晨，李 雨，李聽斌，周奇慧，鄭文鵬

(中國電子科技集團公司第二十一研究所，上海 200233)

0 引 言

近年，隨著我國航天事業的蓬勃發展，吸盤式電磁鐵由于其結構簡單、吸合力大、可靠性高、控制靈活方便，斷電后自動釋放等優點，廣泛用于衛星載荷的鎖定機構、航天器連接——釋放機構，發揮重要作用[1-2]。但由于材料本身特性，電磁鐵斷電后會存在一定的殘余吸力，影響連接——釋放機構的正常釋放動作。機構必須提供較大的驅動力，才可保證電磁鐵和吸盤的分離，或增加彈簧等裝置將電磁鐵和吸盤分開，這導致了機構設計更加復雜，且降低了系統可靠性。本文結合某型號工程需求，分析了電磁鐵斷電殘余吸力的機理和影響因素，在滿足電磁鐵通電吸力的前提下，提出了一種減小吸盤電磁鐵斷電殘余吸力的方法，滿足了工程應用要求。

1 吸盤式電磁鐵結構原理

吸盤式電磁鐵結構如圖1所示，由電磁鐵和吸盤兩部分組成。其中電磁鐵主要由環形線圈、線圈骨架和鐵心構成，吸盤是由軟磁材料根據接口要求設計加工的零件。

線圈通電產生磁場，吸盤與電磁鐵之間產生吸力作用，吸盤與電磁鐵吸合，斷電后吸盤與電磁鐵在外力作用下脫開。

由于電磁鐵鐵心和吸盤所用軟磁材料并非理想材料，存在剩磁[3-4]，電磁鐵即使斷電，電磁鐵與吸盤之間仍然存在吸力，在此稱之為殘余吸力，殘余吸力大小取決于材料的特性。

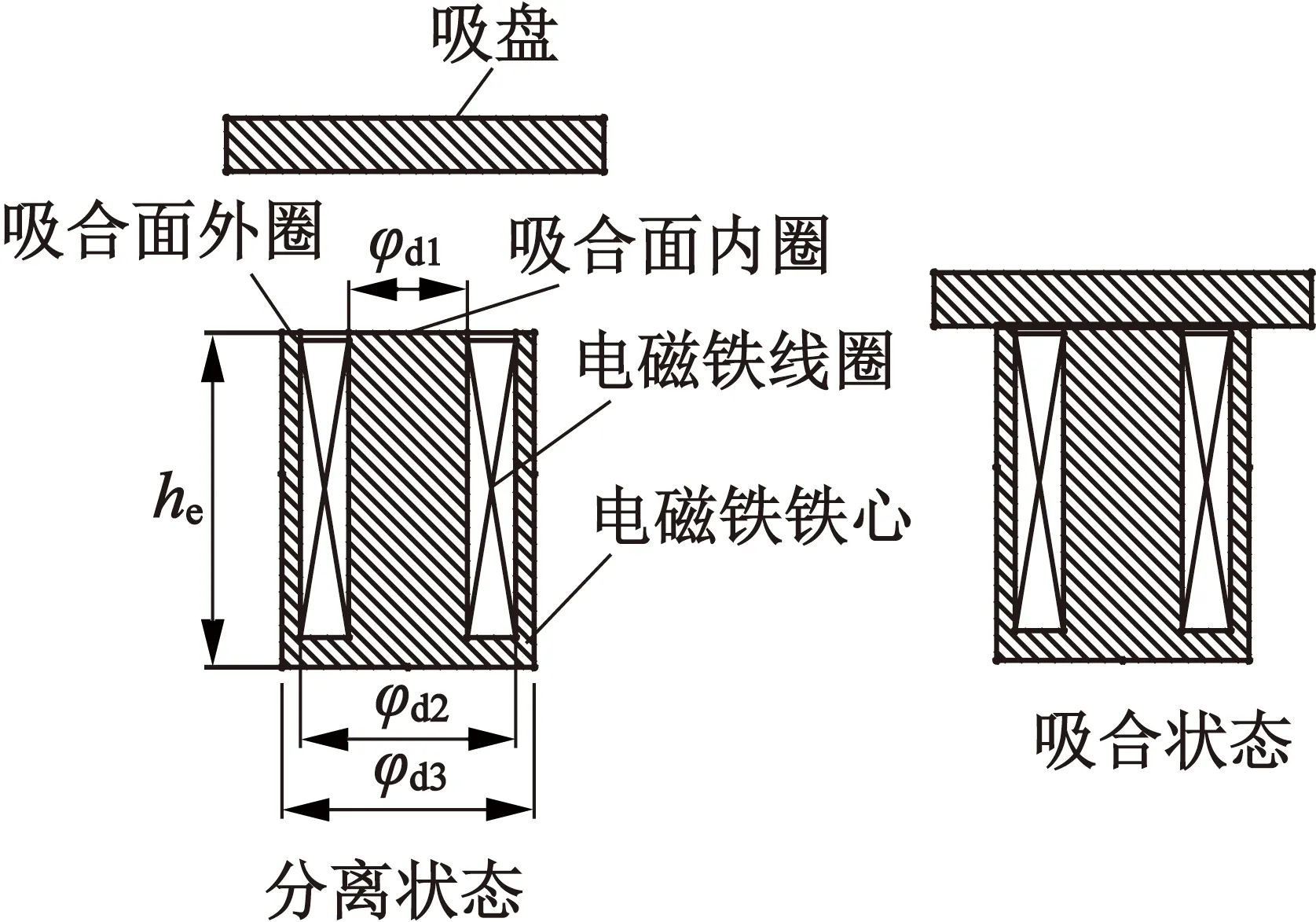
圖1 吸盤式電磁鐵結構原理

2 電磁鐵通電吸力與斷電殘余吸力原理分析

吸盤式電磁鐵電磁吸力公式如下[5]：

(1)

式中：F為電磁吸力；B為接觸面之間氣隙的磁感應強度；S為吸合面有效面積；μ0為真空磁導率，μ0=4π×10-7H/m。

由此可見，電磁鐵和吸盤之間的電磁吸力與接觸面之間的磁感應強度B的平方成正比。為了便于分析，針對圖1的電磁鐵結構，建立通電狀態的等效磁路模型，如圖2所示。

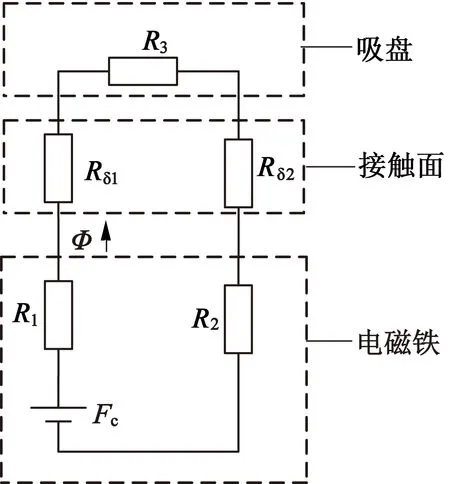
圖2 吸盤式電磁鐵通電狀態等效磁路圖

根據等效磁路模型，可近似計算接觸面之間的磁通和磁感應強度：

(2)

(3)

式中：Fc為電磁鐵線圈磁動勢；R1為電磁鐵鐵心內圈磁阻；R2電磁鐵鐵心外圈磁阻；R3為電磁鐵吸盤磁阻；Rδ1為電磁鐵鐵心內圈與吸盤接觸面氣隙磁阻；Rδ2為電磁鐵鐵心外圈與吸盤接觸面氣隙磁阻；Φ為主磁路磁通。

當電磁鐵斷電時，考慮到軟磁材料的磁滯特性，磁滯曲線如圖3所示[6-7]，圖2中的線圈磁動勢Fc消失，但磁回路中仍然存在磁動勢，可將電磁鐵鐵心和吸盤看成矯頑力(Hc)和剩磁(Br)較低的永磁材料[8]，等效磁路如圖4所示。

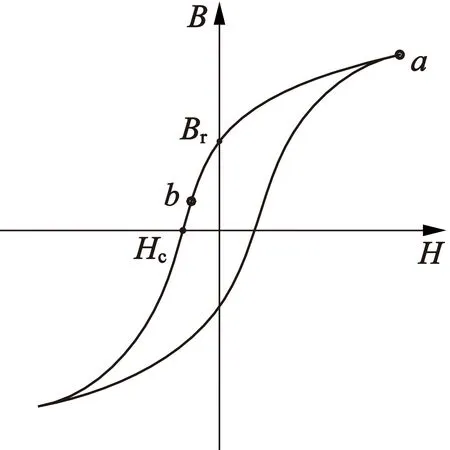
圖3 軟磁材料的磁滯曲線

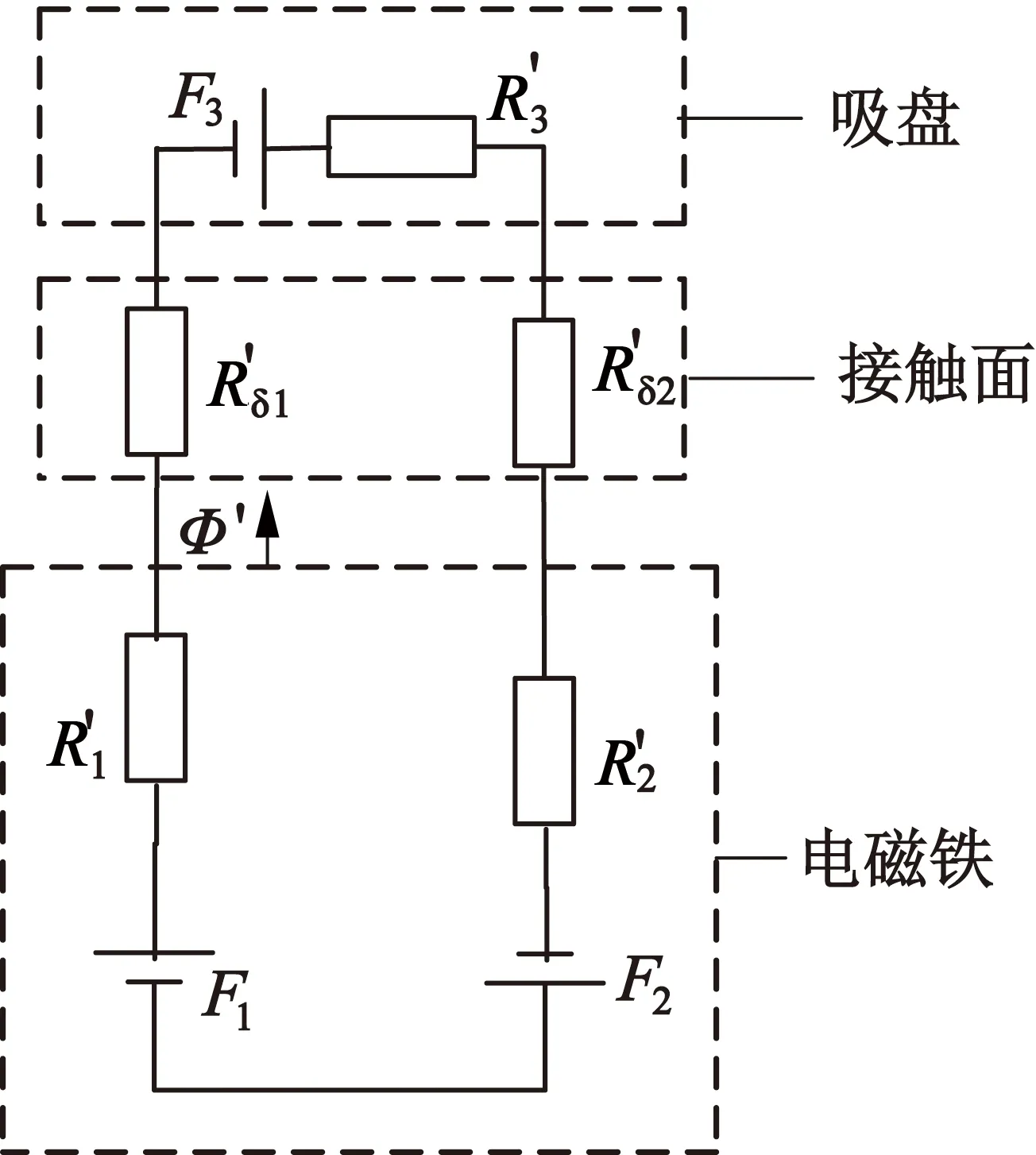
圖4 吸盤式電磁鐵斷電狀態等效磁路圖

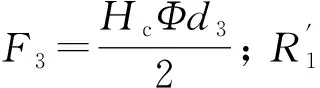
根據等效磁路模型，可近似計算接觸面之間的磁通和磁感應強度：

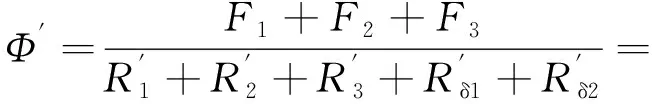
(4)

(5)

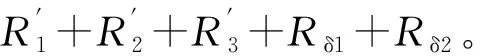
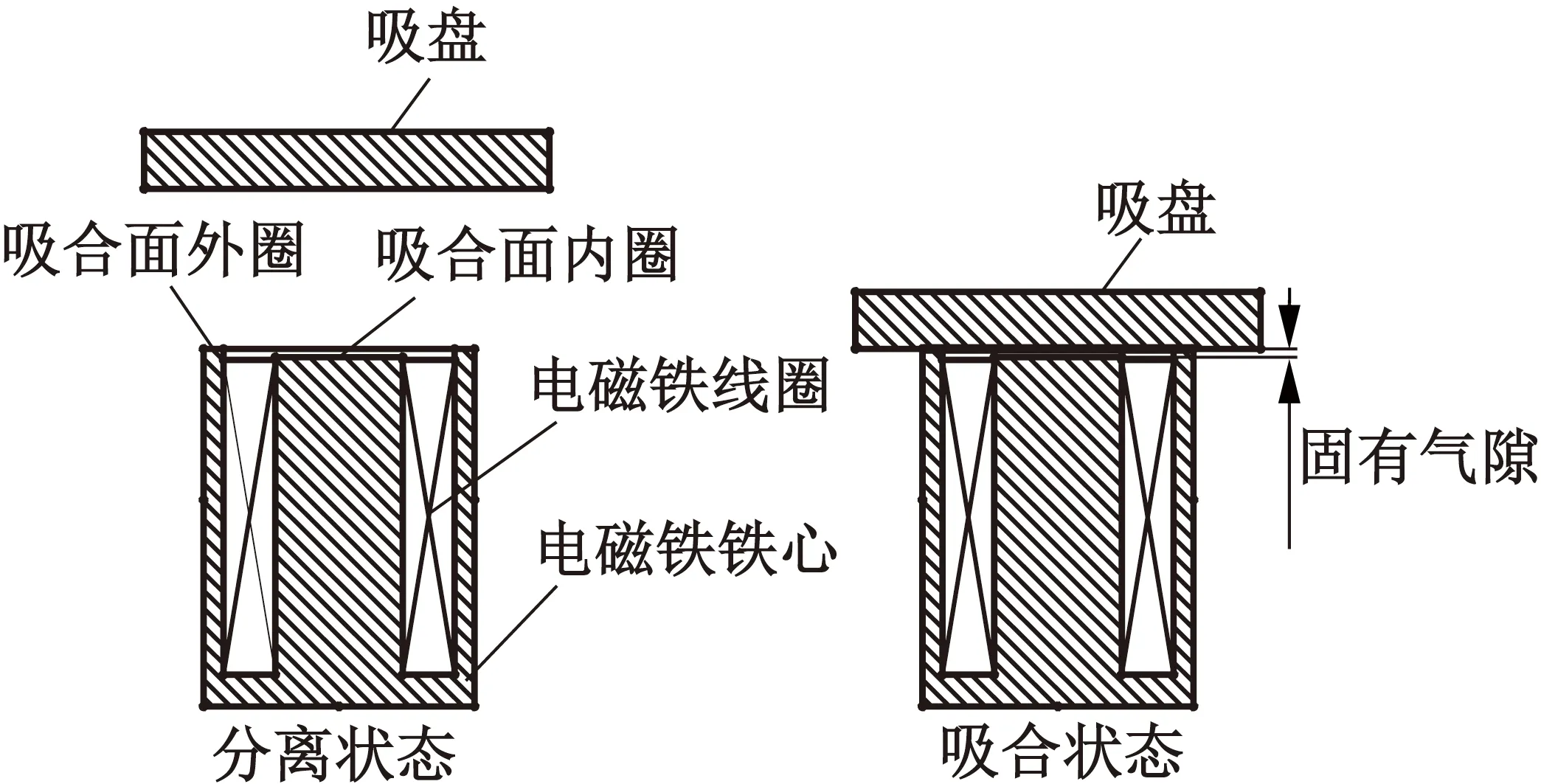
圖5 增加固有氣隙的吸盤式電磁鐵結構原理

3 設計仿真

針對上文分析，本文建立了電磁鐵的通電斷開狀態有限元模型如圖6、圖7所示。斷電狀態的有限元模型與通電狀態模型的不同之處在于斷電狀態線圈內安匝數為0，內鐵心、外鐵心和吸盤材料參數由軟磁材料的直流磁化特性變為永磁材料的剩磁、矯頑力以及相對回復磁導率，磁化方向與通電狀態主磁路磁化方向一致。電磁鐵模型基本參數如表1所示。

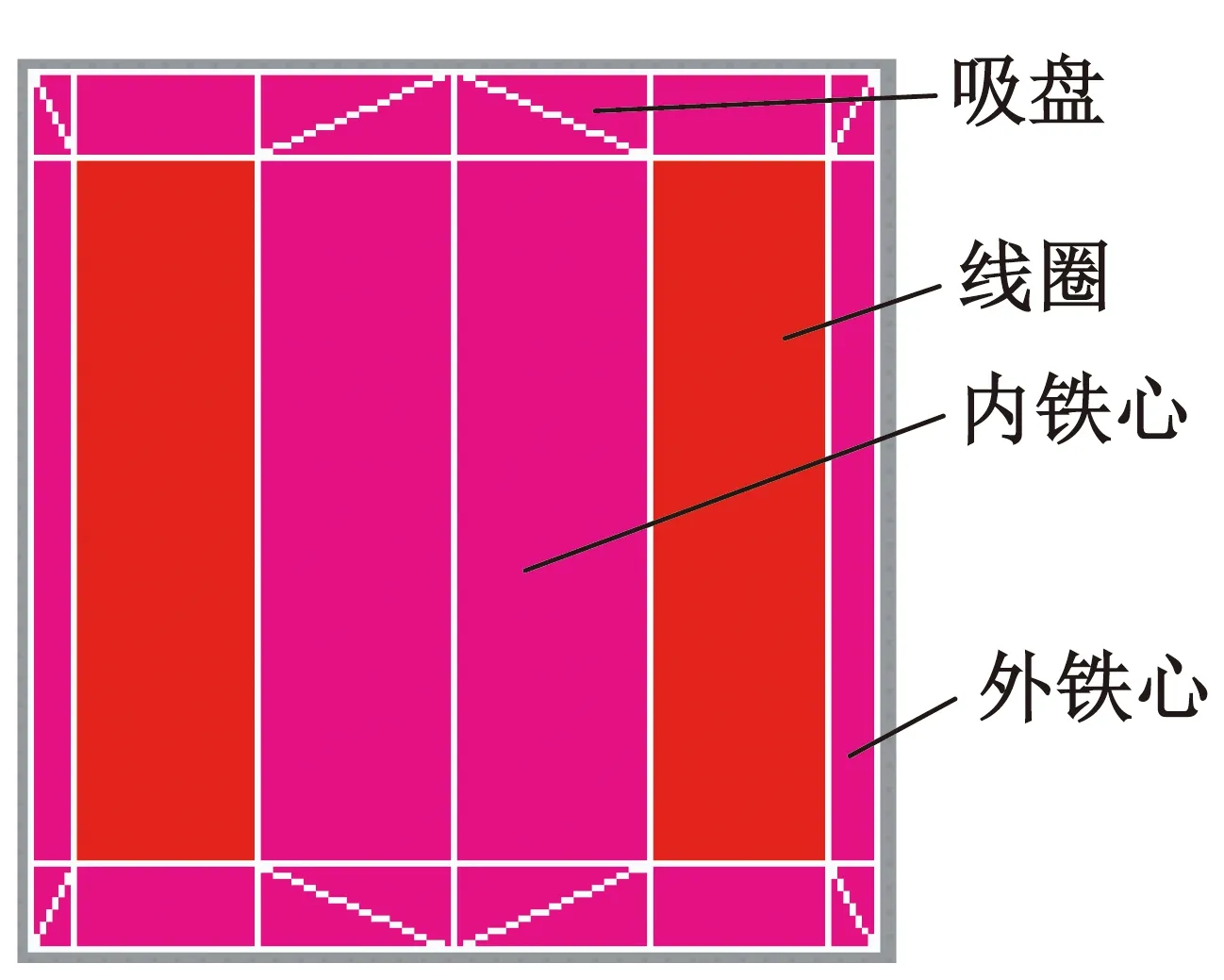
圖6 電磁鐵通電有限元模型

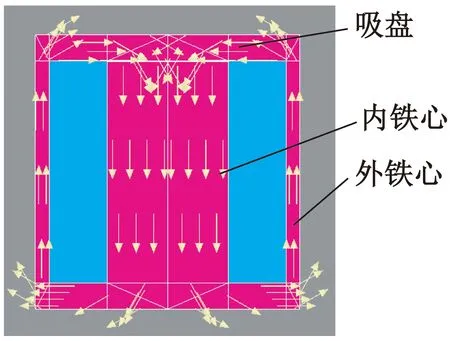
圖7 電磁鐵斷電有限元模型

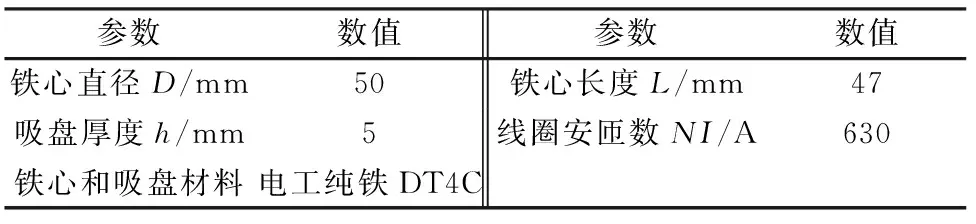
表1 吸盤電磁鐵模型基本參數

改變模型中固有氣隙δ1的數值分別計算通電吸力和斷電殘余吸力，分別得到通電吸力和斷電殘余吸力隨固有氣隙δ1的變化關系如圖8、圖9所示，計算結果如表2所示。

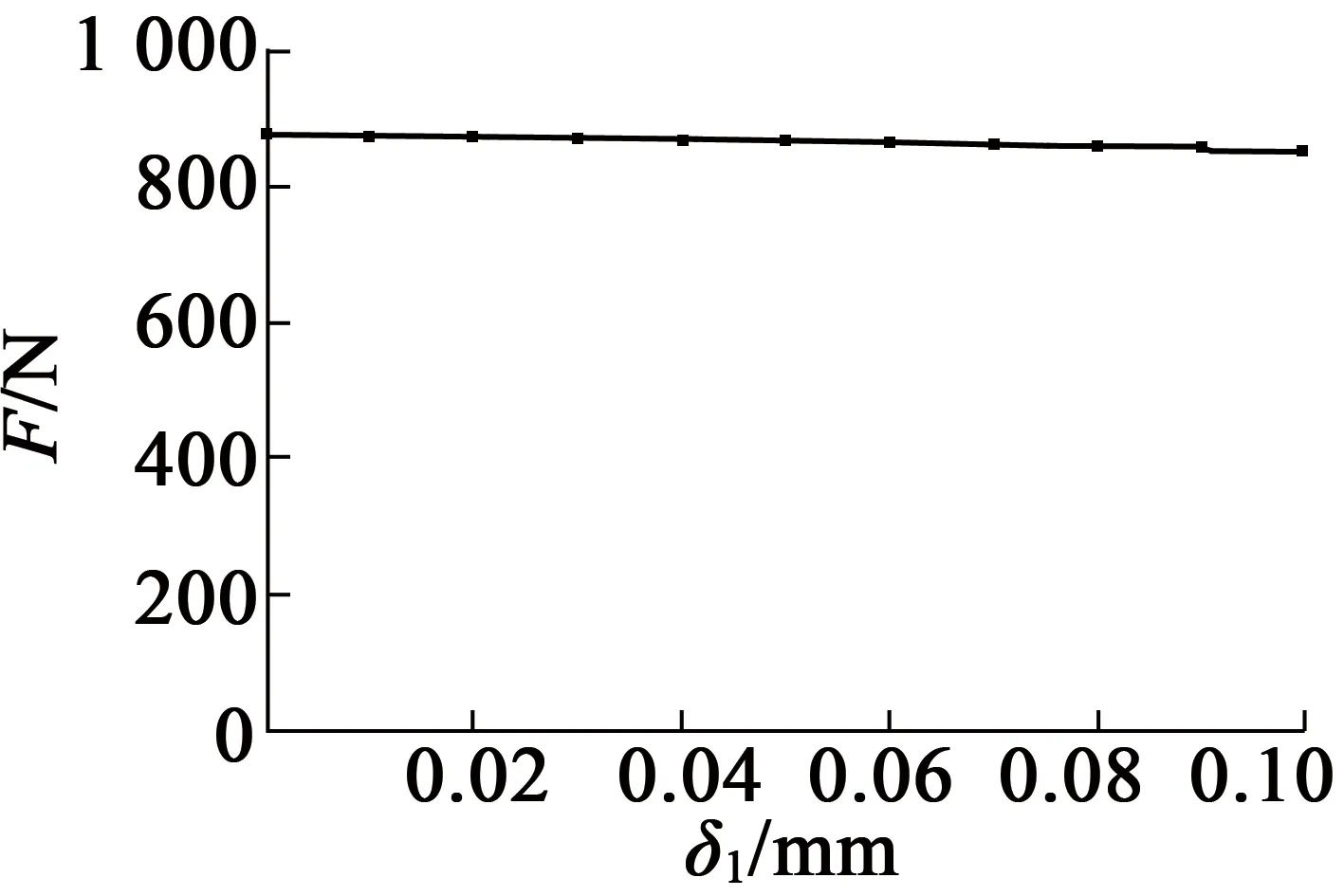
圖8 電磁鐵通電吸力隨附加氣隙的變化曲線

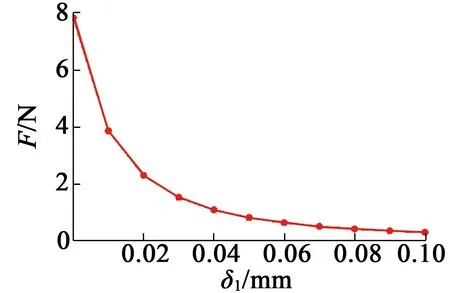
圖9 電磁鐵斷電殘余吸力隨附加氣隙的變化曲線

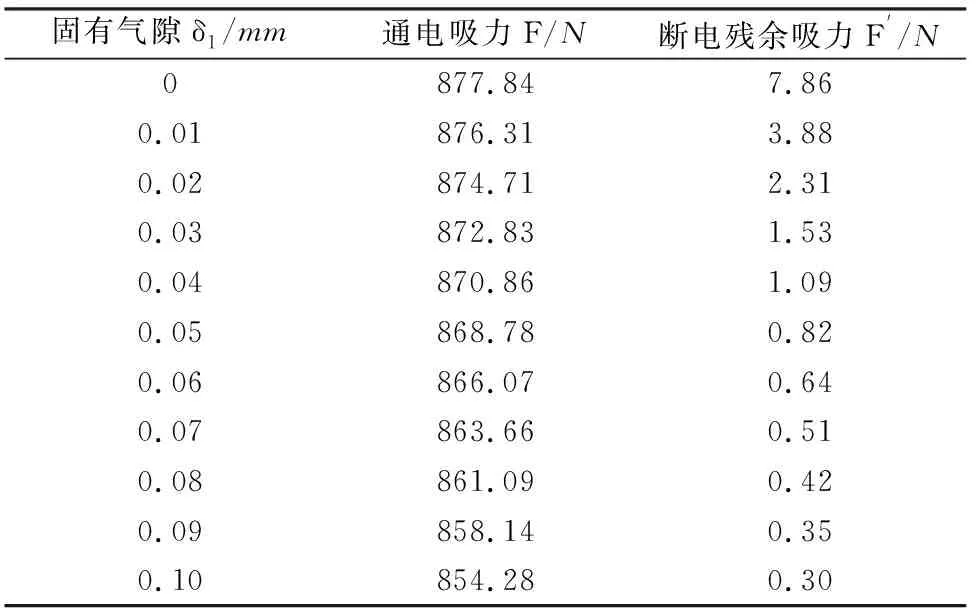
表2 通電吸力和斷電殘余吸力有限元計算結果

從表2中可以看出，當固有氣隙δ1在0～0.1 mm范圍內變化時，電磁鐵通電吸力變化不大，而斷電殘余吸力迅速減小，與磁路分析所得結論一致。

4 樣機實例

根據上述分析，研制了2臺樣機。1#樣機電磁鐵內外鐵心平齊，2#樣機電磁鐵鐵心內鐵心比外鐵心低0.04 mm。根據2臺樣機參數建立了有限元模型，計算結果如表3所示。

表3 樣機模型的有限元計算結果

通過拉壓力傳感器對電磁鐵通電吸力測試如圖10所示，斷電殘余吸力通過吸盤下懸掛砝碼的方式進行測試，如圖11所示，測試結果如表4所示。

圖10 電磁鐵通電吸力測試

圖11 電磁鐵斷電殘余吸力測試

表4 樣機測試結果

樣機測試結果與有限元計算結果相差不大，同樣證明了通過在鐵心中增加固有氣隙的方式可以在損失一小部分通電吸力的情況下，大大減小斷電殘余吸力。

5 結 語

吸盤式電磁鐵由于材料本身的特性，存在斷電殘余吸力，在對斷電釋放有特殊要求的場合需要加以考慮。本文通過理論分析建立了電磁鐵開通斷電的磁路模型，分析了吸盤式電磁鐵斷電殘余吸力的特性，提出了一種通過增加固有氣隙的方式減小斷電殘余吸力的方法，有限元仿真計算和樣機實測表明該方法簡單有效。