電機槽極配合與電機運行質(zhì)量特性研究(I)

邱國平,王 鎮(zhèn),丁 立

(1.常州亞美柯寶馬電機有限公司，常州 213011；2. 常州旭泉精密電機有限公司，常州 213011)

編者按：永磁同步電機的運行質(zhì)量特性是電機設(shè)計生產(chǎn)制造等方面的關(guān)注焦點之一。以本期開始，我刊將分期刊登由邱國平等撰寫的有關(guān)永磁同步電機槽極配合與電機運行質(zhì)量特性研究應(yīng)用方面的文章，以期對從事電機研究和設(shè)計有興趣的讀者有所參考，更好地滿足用戶和市場的需求。

1 電機運行特性

1.1 電機運行的機械特性

電機在運行中表現(xiàn)出的特性，一般稱為電機的機械特性，電機的機械特性決定了電機在不同工作點的性能，其中包括：轉(zhuǎn)矩、轉(zhuǎn)速、電流、輸出功率、輸入功率等。電機的機械特性曲線決定了電機運行時的機械性能。圖1是某型號24槽20極永磁同步電機的機械特性曲線。

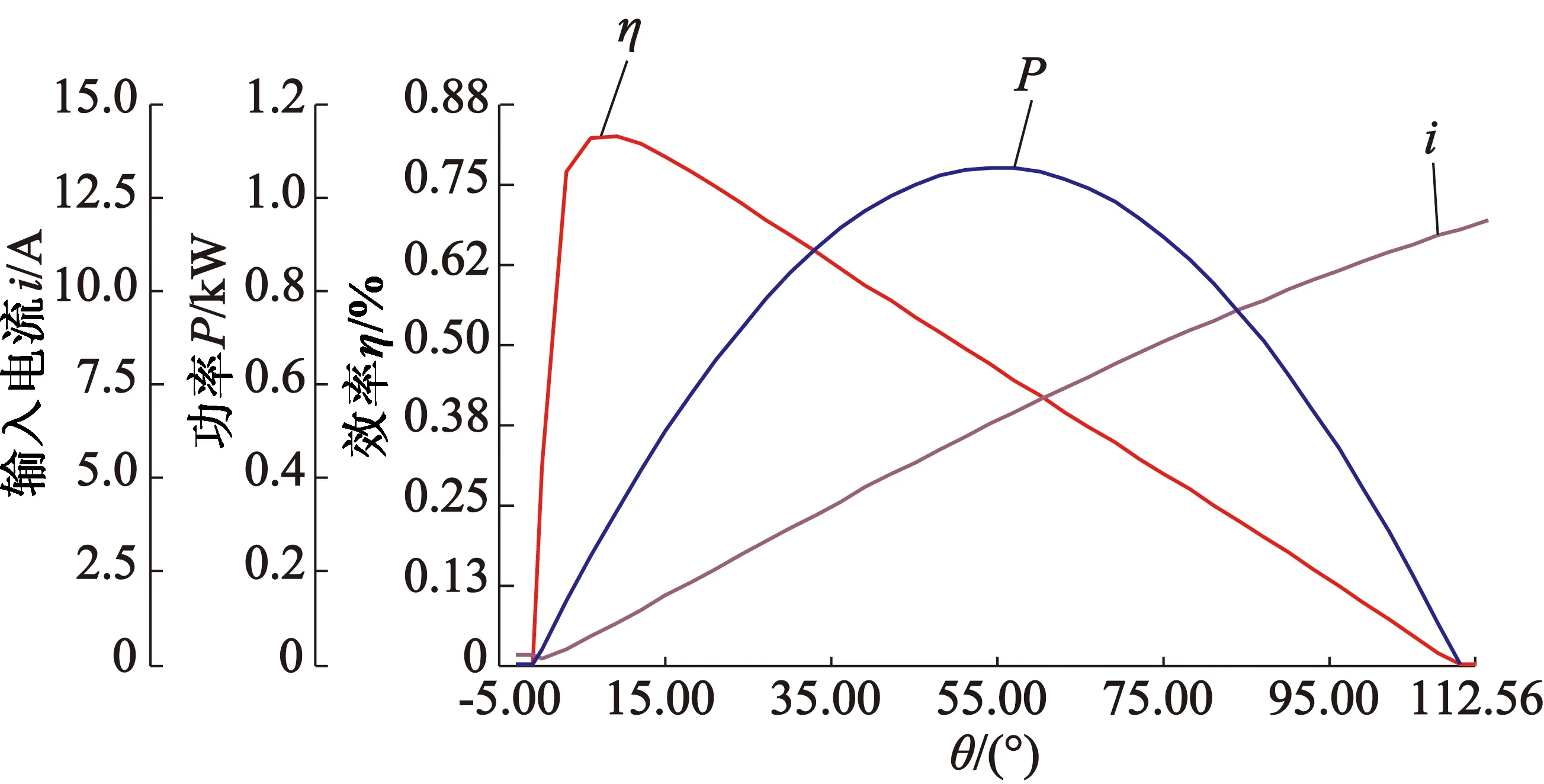
圖1 電機機械特性曲線圖

電機的機械特性主要是由電機的轉(zhuǎn)矩常數(shù)KT和感應(yīng)電動勢常數(shù)KE所決定的[1]：

(1)

式中：N為電機有效導體根數(shù)；Φ為電機有效工作磁通；NΦ為電機磁鏈。

可見，電機運行的機械特性是由電機的有效導體根數(shù)和有效工作磁通這兩個因素決定的。因此，只要控制好電機的磁鏈，就能基本確定電機運行的機械特性。

1.2 電機運行質(zhì)量特性

電機設(shè)計工作者往往用較大的精力去分析、研究如何設(shè)計出能達到機械特性要求的電機。但是，即使在設(shè)計上實現(xiàn)良好的電機機械特性,也并不是電機設(shè)計的全部。例如兩輛汽車同樣能達到80 km/h，一輛車在運行過程中非常平穩(wěn)，噪聲小；另一輛車在運行中，振動大，噪聲也大，運行不平穩(wěn)，那么這兩輛車的運行性能是有差別的，其差別不是在汽車的運行車速上，而是在汽車運行質(zhì)量上。

電機也一樣，具有相同機械特性的電機，有的運行平穩(wěn)，有的會產(chǎn)生有較大的齒槽轉(zhuǎn)矩、轉(zhuǎn)矩波動、較多的高次諧波、振動、噪聲等，這就是電機的本身運行質(zhì)量特性差別的緣故。

因此，除了要考核電機的運行機械特性，還得考核電機的運行質(zhì)量特性，兩者不可偏廢。

電機的運行質(zhì)量特性是電機的內(nèi)特性，它是由電機的某些重要因素所控制的。電機的質(zhì)量特性包括：齒槽轉(zhuǎn)矩、轉(zhuǎn)矩波動、諧波、感應(yīng)電動勢和波形、最大輸出功率等。本文研究的電機質(zhì)量特性是由電機的槽數(shù)、極數(shù)配合所決定的,也就是說電機的運行質(zhì)量的好壞與電機選取某種槽、極配合有著重大關(guān)系。如果電機槽、極配合較好，那么電機的齒槽轉(zhuǎn)矩等質(zhì)量特性就好；如果電機槽、極配合沒有選好，那么電機的齒槽轉(zhuǎn)矩、轉(zhuǎn)矩波動就大，諧波就多，感應(yīng)電動勢正弦度就差，控制困難等情況會非常嚴重。在不妥當?shù)牟邸O配合的電機上，即使采取許多措施，也難以取得理想的電機運行質(zhì)量性能。

在改善電機的機械特性時，抓住電機的N，Φ兩大要素，控制電機的KT和KE，也就控制了電機的運行機械性能。在設(shè)計電機時，選定合理的槽、極配合，從而可以得到良好的電機運行質(zhì)量特性；在此基礎(chǔ)上再進行電機結(jié)構(gòu)和其他參數(shù)的設(shè)計，不必為了改善電機運行質(zhì)量特性而增加許多額外措施。

下面用電機的槽、極配合來控制電機運行質(zhì)量特性，作如下專題介紹。

2 電機結(jié)構(gòu)與槽極配合

一般，電機主要由定子和轉(zhuǎn)子組成，如果是有槽電機，則電機定子要在槽內(nèi)嵌入一定數(shù)量的繞組導體。永磁同步電機或無刷電機的結(jié)構(gòu)基本是由電機定子、定子繞組、轉(zhuǎn)子、轉(zhuǎn)子磁極、軸、端蓋等零件組成，如圖2所示。電機轉(zhuǎn)子和定子產(chǎn)生的轉(zhuǎn)矩由轉(zhuǎn)子軸輸出，端蓋支撐轉(zhuǎn)子轉(zhuǎn)動。圖3是電機的定、轉(zhuǎn)子沖片和磁鋼結(jié)構(gòu)圖。

圖2 永磁同步電動機結(jié)構(gòu)圖

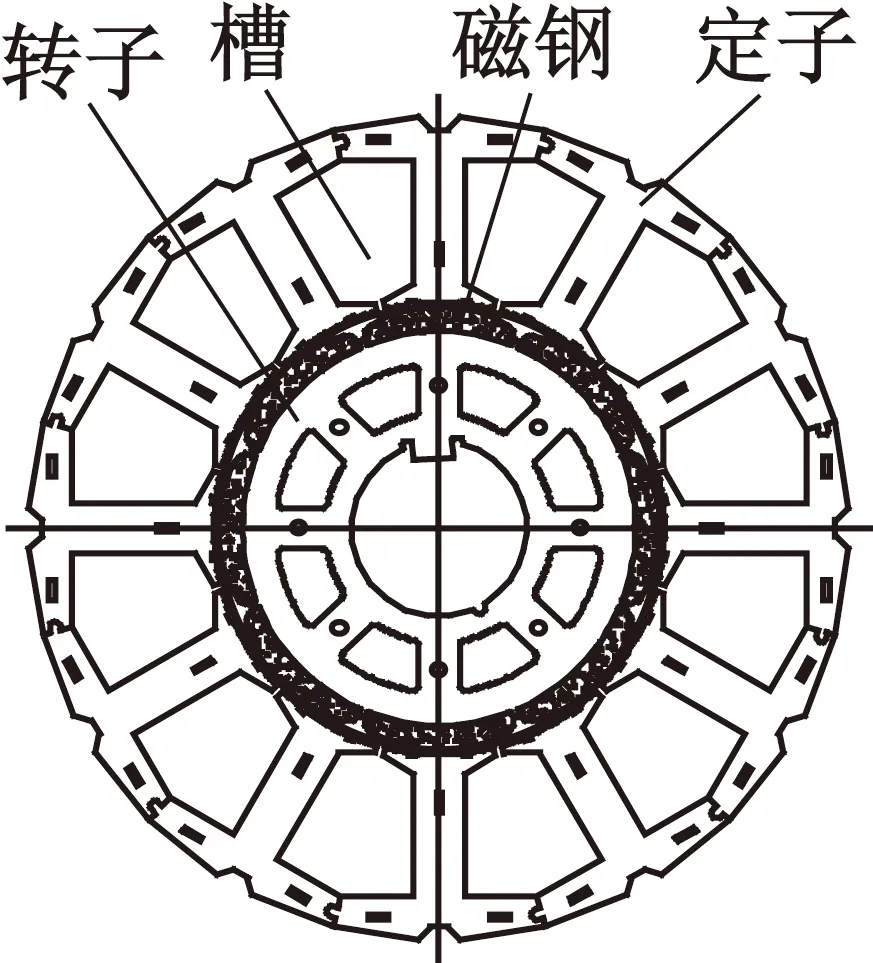
圖3 電動機定轉(zhuǎn)子結(jié)構(gòu)圖

2.1 電機槽極配合與電機性能、工藝的關(guān)系

電機的槽極是組成電機的重要因素，不同的電機往往會采用不同的槽極配合。電機槽極配合是否合適，對電機的運行質(zhì)量特性和制作工藝影響較大，只有對電機的槽極配合有一個清晰了解和分析，才能較好地獲得合理的槽極配合，并能對某些電機的槽極配合作出分析和判斷。

電機槽極配合會影響到電機的運行質(zhì)量參數(shù)，主要有：齒槽轉(zhuǎn)矩、轉(zhuǎn)矩波動、繞組系數(shù)、最大輸出功率、感應(yīng)電動勢、諧波等。電機槽極配合合理，可得到較小的齒槽轉(zhuǎn)矩，且齒槽轉(zhuǎn)矩的正弦度好，電機轉(zhuǎn)子就不需要用多段直極錯位，也不要在磁鋼上進行偏心、削角等措施來減弱電機的齒槽轉(zhuǎn)矩。合理的槽極配合能簡化電機繞組和電機下線工藝，可大大降低電機制作成本，有利于后續(xù)的設(shè)計優(yōu)化。

2.2 齒槽轉(zhuǎn)矩

齒槽轉(zhuǎn)矩是電機轉(zhuǎn)子的極在旋轉(zhuǎn)時，通過定子的齒和磁極相互作用產(chǎn)生的轉(zhuǎn)矩[2]。電機的轉(zhuǎn)子在不通電和通電時,齒槽轉(zhuǎn)矩都存在。一個電機在不通電時，擰動電機軸，使轉(zhuǎn)子轉(zhuǎn)動，發(fā)現(xiàn)轉(zhuǎn)動時有一個阻力，阻力有大有小，大的要費很大的勁才能擰動轉(zhuǎn)子；有時擰動轉(zhuǎn)子很輕松，而且擰動時發(fā)現(xiàn)轉(zhuǎn)子會有不均勻的、有規(guī)則的阻力波動，這種阻力就是電機的齒槽轉(zhuǎn)矩。

2.3 關(guān)于分段直極錯位的概念

要削弱電機的齒槽轉(zhuǎn)矩，可以采用定子斜槽或轉(zhuǎn)子斜極一定圓心角的方法，如圖4所示。考慮到工藝問題，往往采用電機轉(zhuǎn)子分段直極錯位，這是一種有效削弱電機齒槽轉(zhuǎn)矩的方法[3]，轉(zhuǎn)子分段直極錯位有兩種方法，如圖5所示。現(xiàn)在普遍選用轉(zhuǎn)子直極錯位法1作為轉(zhuǎn)子直極錯位的方法。

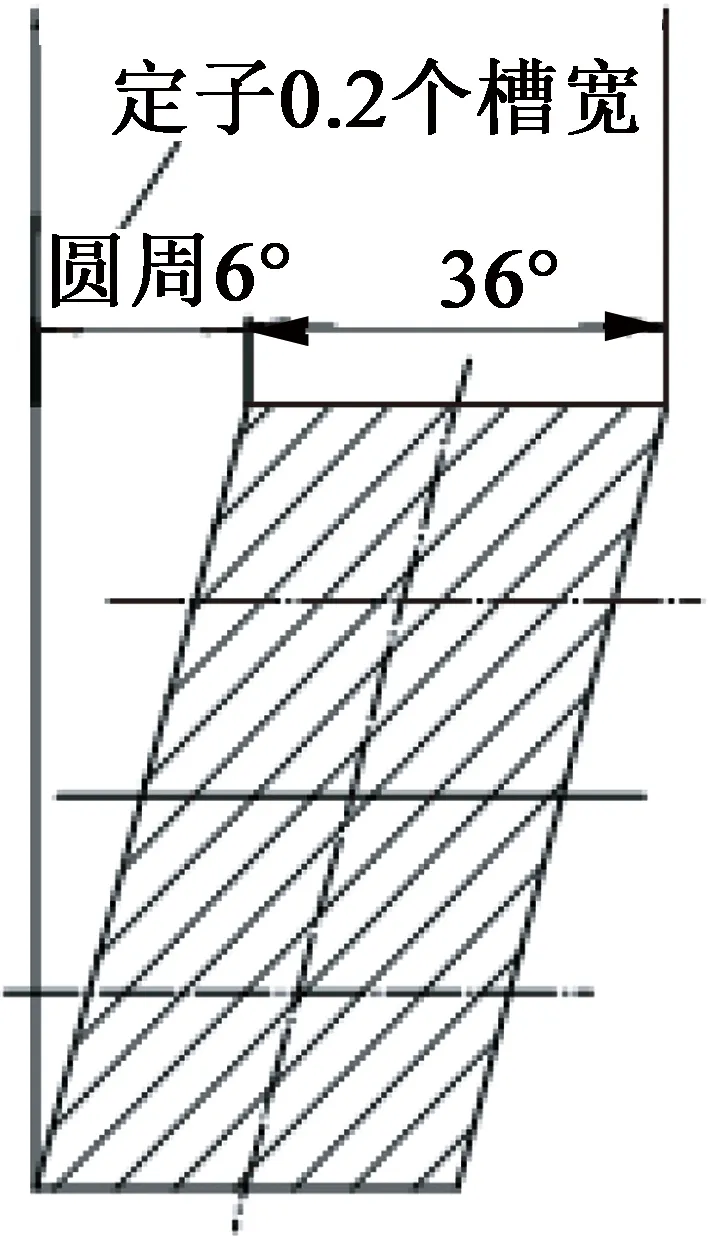
圖4 轉(zhuǎn)子整塊斜極

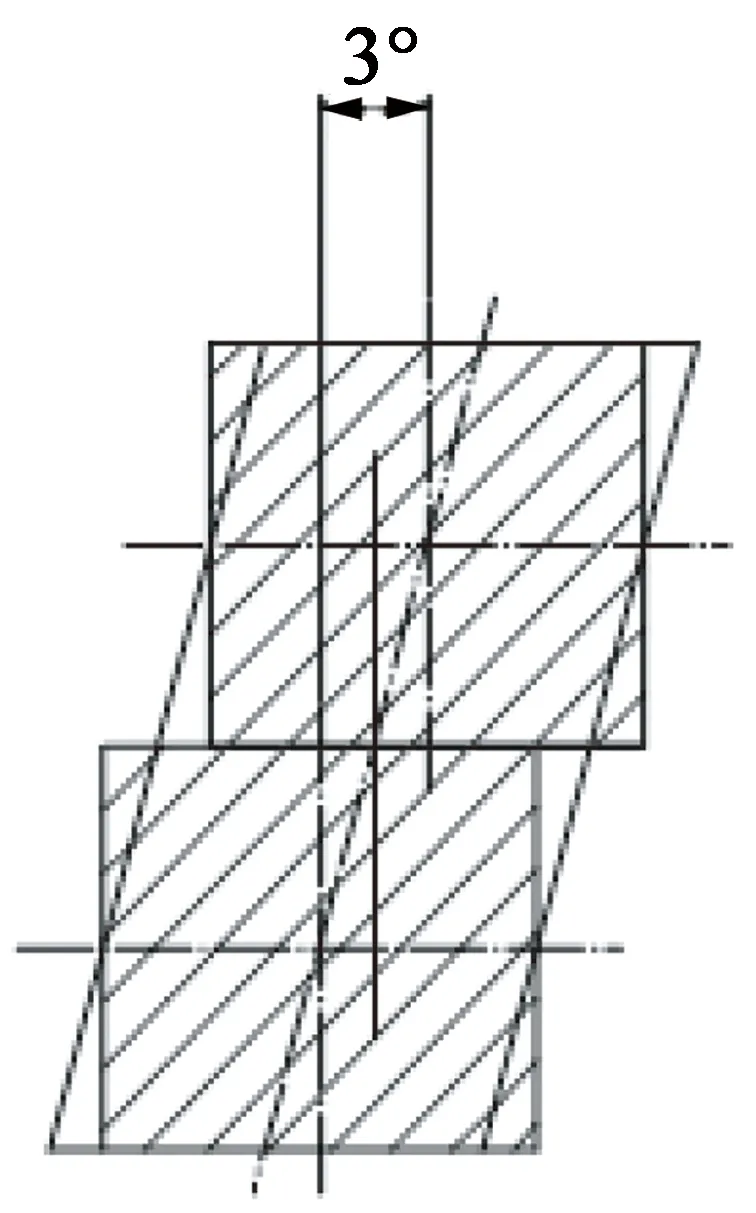
(a) 轉(zhuǎn)子直極錯位法1

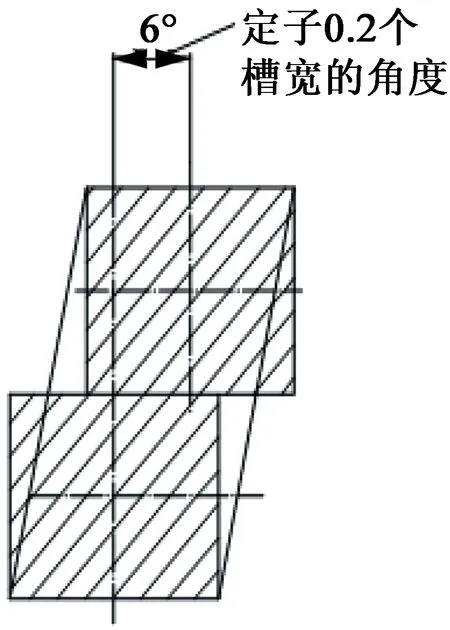
(b) 轉(zhuǎn)子直極錯位法2

2.4 齒槽轉(zhuǎn)矩的整段斜槽度數(shù)和轉(zhuǎn)子分段數(shù)確定

消除電機齒槽轉(zhuǎn)矩基波的斜槽度數(shù)可以從下式求出：

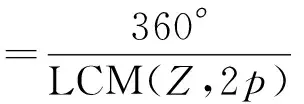
兩段磁鋼中心錯位角度=定子斜槽度數(shù)/分段數(shù)=

磁鋼中心總錯位角度=

兩段磁鋼中心總錯位角度×(分段數(shù)-1)=

式中：LCM(Z,2p)表示齒數(shù)和極數(shù)的最小公倍數(shù)；LF表示轉(zhuǎn)子分段數(shù)。如12槽8極電機，分3段直極錯位，則定子斜槽度數(shù)(圓心角)=15°，磁鋼中心錯位角度=5°，磁鋼中心總錯位角度=10°，其整段錯位和分段錯位圖如圖6、圖7所示。

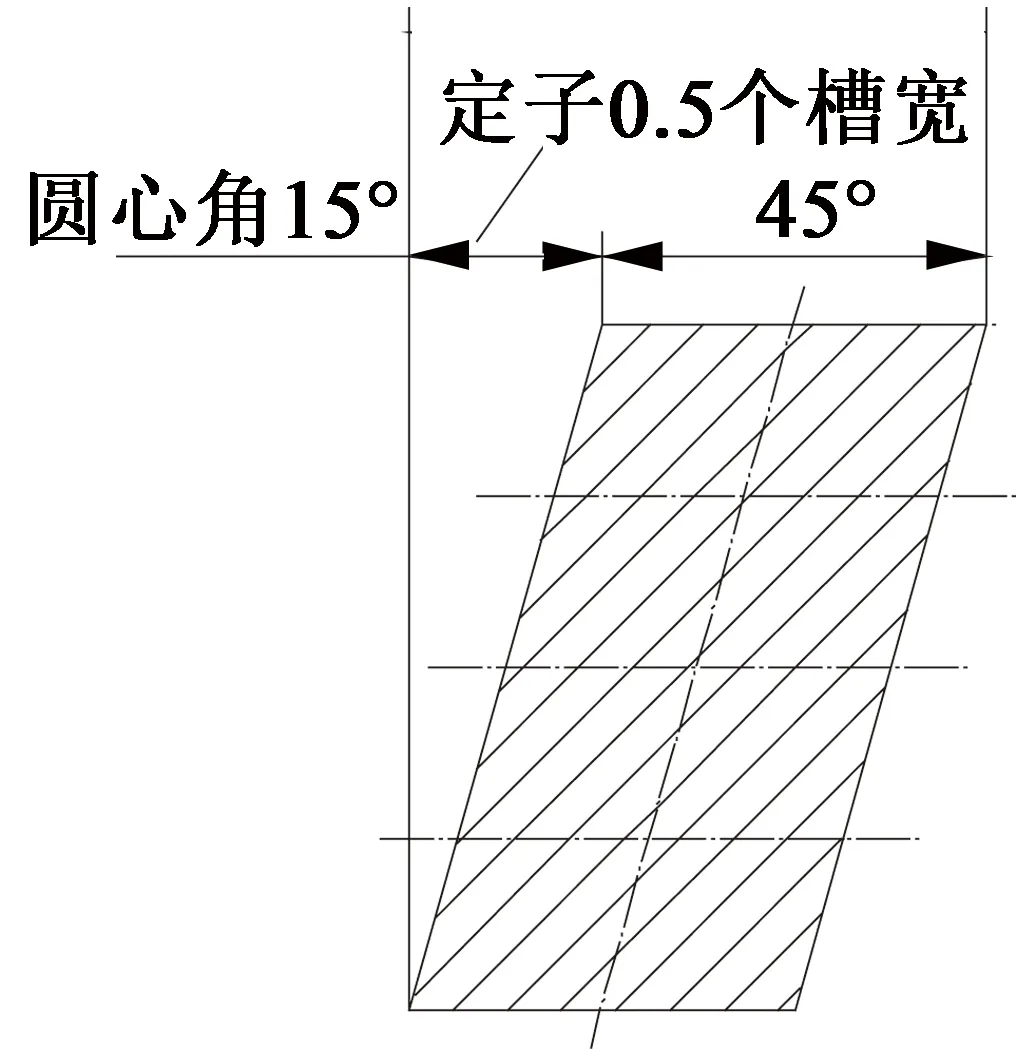
圖6 轉(zhuǎn)子整段斜極

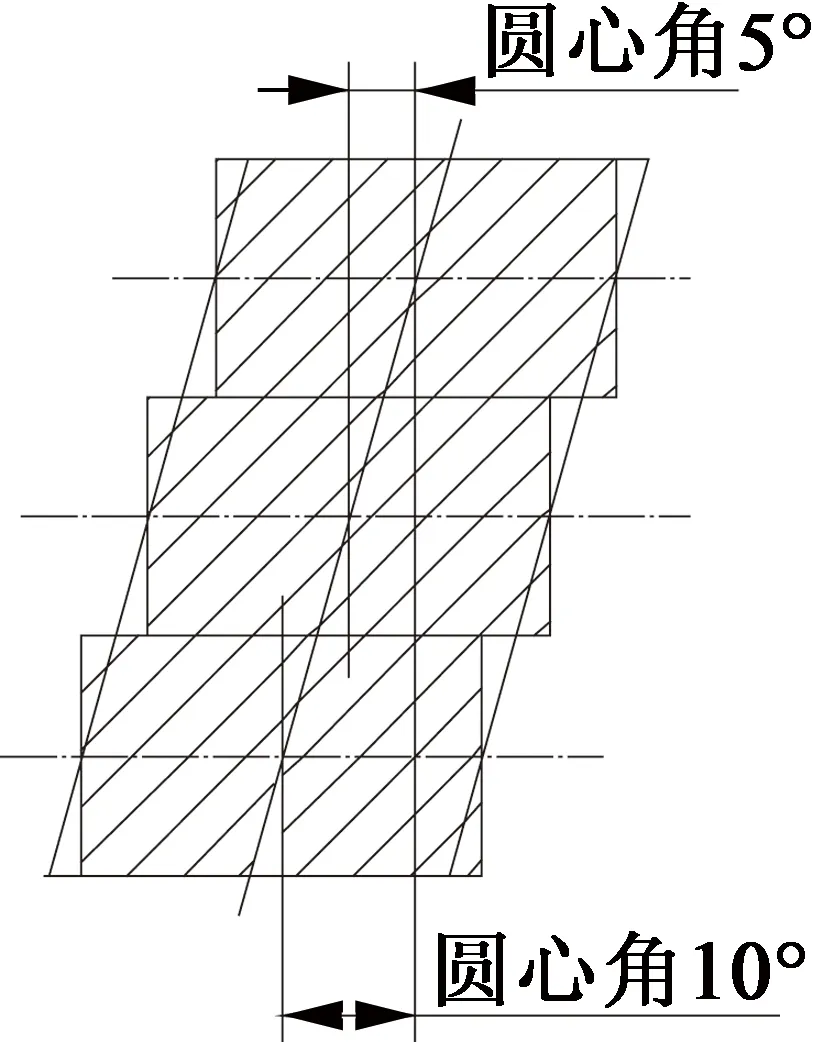
圖7 轉(zhuǎn)子三段直極錯位

可以對電機轉(zhuǎn)子斜極的齒槽轉(zhuǎn)矩進行參數(shù)化分析，求取能兼顧電機其他性能的較好的斜極角度。

電機轉(zhuǎn)子分段斜極的齒槽轉(zhuǎn)矩是轉(zhuǎn)子多個分段或多個整段不斜極轉(zhuǎn)子的齒槽轉(zhuǎn)矩的平均值的合成，因此，電機不斜槽的齒槽轉(zhuǎn)矩波形對合成后的齒槽轉(zhuǎn)矩波形影響較大，如果不斜槽時的齒槽轉(zhuǎn)矩波形正弦度較好，那么電機2段直極錯位后的齒槽轉(zhuǎn)矩將較好。

2.5 齒槽轉(zhuǎn)矩的計算問題

電機的齒槽轉(zhuǎn)矩計算可以用路或2D場計算。在電機設(shè)計時用路計算，觀察一個電機齒槽轉(zhuǎn)矩的總體趨勢，必要時用2D場分析對電機的齒槽轉(zhuǎn)矩進行計算。各種軟件計算電機的齒槽轉(zhuǎn)矩還是不一致。同一電機模塊，用Maxwell 2D和Motor-CAD在2段直極錯位時計算的齒槽轉(zhuǎn)矩相差不大，在6段直極錯位時就相差較大了。在電機的生產(chǎn)制造過程中還有多種因素影響電機的齒槽轉(zhuǎn)矩，所以實際齒槽轉(zhuǎn)矩要比計算所得的大。

2.6 齒槽轉(zhuǎn)矩的評價因子CT

電機槽數(shù)Z和極數(shù)2p對電機齒槽轉(zhuǎn)矩有較大的影響。以電機的定子槽數(shù)Z和極數(shù)2p的最大公約數(shù)作為電機齒槽轉(zhuǎn)矩的評價因子CT，評價因子越小，齒槽轉(zhuǎn)矩的峰值就越低，即電機的齒槽轉(zhuǎn)矩就越小。這是電機槽極配合與電機齒槽轉(zhuǎn)矩的主要內(nèi)在關(guān)系。CT與電機槽極的關(guān)系式如下[4]：

CT=GCD(Z,2p)

式中：GCD(Z,2p)是電機槽數(shù)Z、極數(shù)2p的最大公約數(shù)。

不論電機是整數(shù)槽還是分數(shù)槽，CT=GCD(Z,2p)都是適用的。

即使評價因子CT為同一等級，電機的齒槽轉(zhuǎn)矩也有差別，但相差會小于其他等級的評價因子的齒槽轉(zhuǎn)矩。

12槽電機的齒槽轉(zhuǎn)矩和評價因子如表1所示。

表1 12槽電機的評價因子CT和齒槽轉(zhuǎn)矩

2.7 齒槽轉(zhuǎn)矩周期波動數(shù)

表貼式集中繞組電機的齒槽轉(zhuǎn)矩表達式[1]：

(2)

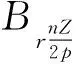
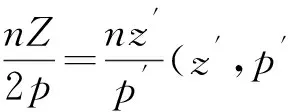
γ=2pZ/GCD(Z,2p)=LCM(Z,2p)

一個槽的基波齒槽轉(zhuǎn)矩周期數(shù)[1]：

Np=γ/Z=2p/GCD(Z,2p)

就是說,一個槽的基波齒槽轉(zhuǎn)矩周期波動數(shù)是極數(shù)除以槽數(shù)和極數(shù)的最大公約數(shù)。那么兩個槽的基波齒槽轉(zhuǎn)矩周期數(shù)就是2Np。

例如，12槽8極電機的齒槽轉(zhuǎn)矩周期數(shù)2Np=2×2=4,有8個脈沖，上下各4個。

表2是電機不同槽極配合下齒槽轉(zhuǎn)矩評價因子CT和兩齒槽轉(zhuǎn)矩周期波動數(shù)2Np。

表2中，12槽10極和12槽14極的評價因子CT相同(CT=2)，但是兩者的兩齒槽轉(zhuǎn)矩周期波動數(shù)2Np不同，周期波動數(shù)多，則電機的齒槽轉(zhuǎn)矩要小。

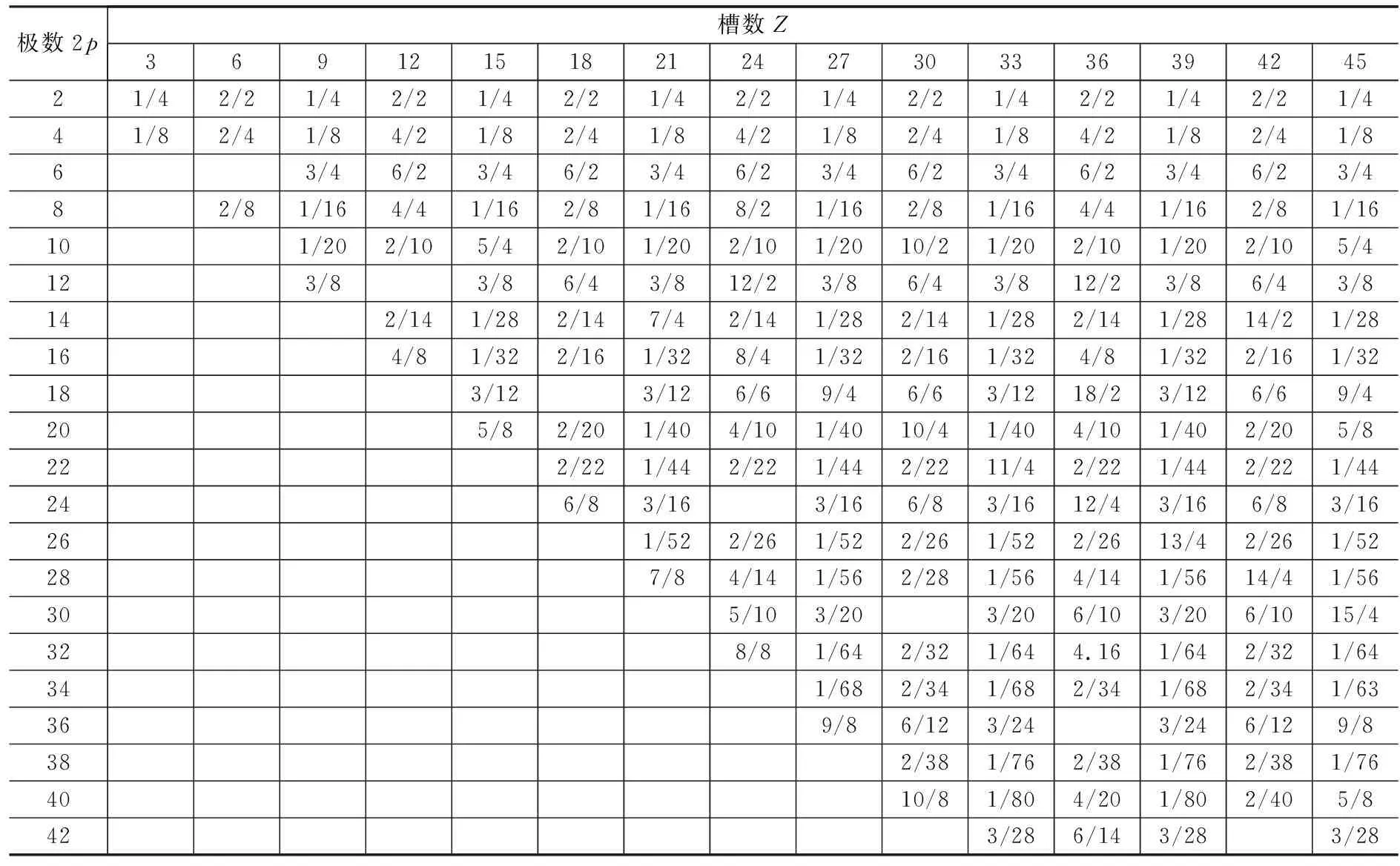
表2 極槽配合齒槽轉(zhuǎn)矩評價因子CT和兩齒槽轉(zhuǎn)矩周期波動數(shù)2Np

2.8 齒槽轉(zhuǎn)矩的計算因子KL

齒槽轉(zhuǎn)矩呈周期性的變化，提高LCM(Z,2p)，使基波得到提高，從而抑制其他高次諧波，電機的齒槽轉(zhuǎn)矩得到改善。以電機的槽數(shù)與槽極數(shù)的最小公倍數(shù)之比KL作為判斷電機齒槽轉(zhuǎn)矩更精細的依據(jù)，KL稱為電機齒槽轉(zhuǎn)矩的計算因子，KL越小，則電機齒槽轉(zhuǎn)矩就越小。

表3為不同槽極配合下的齒槽轉(zhuǎn)矩計算因子。

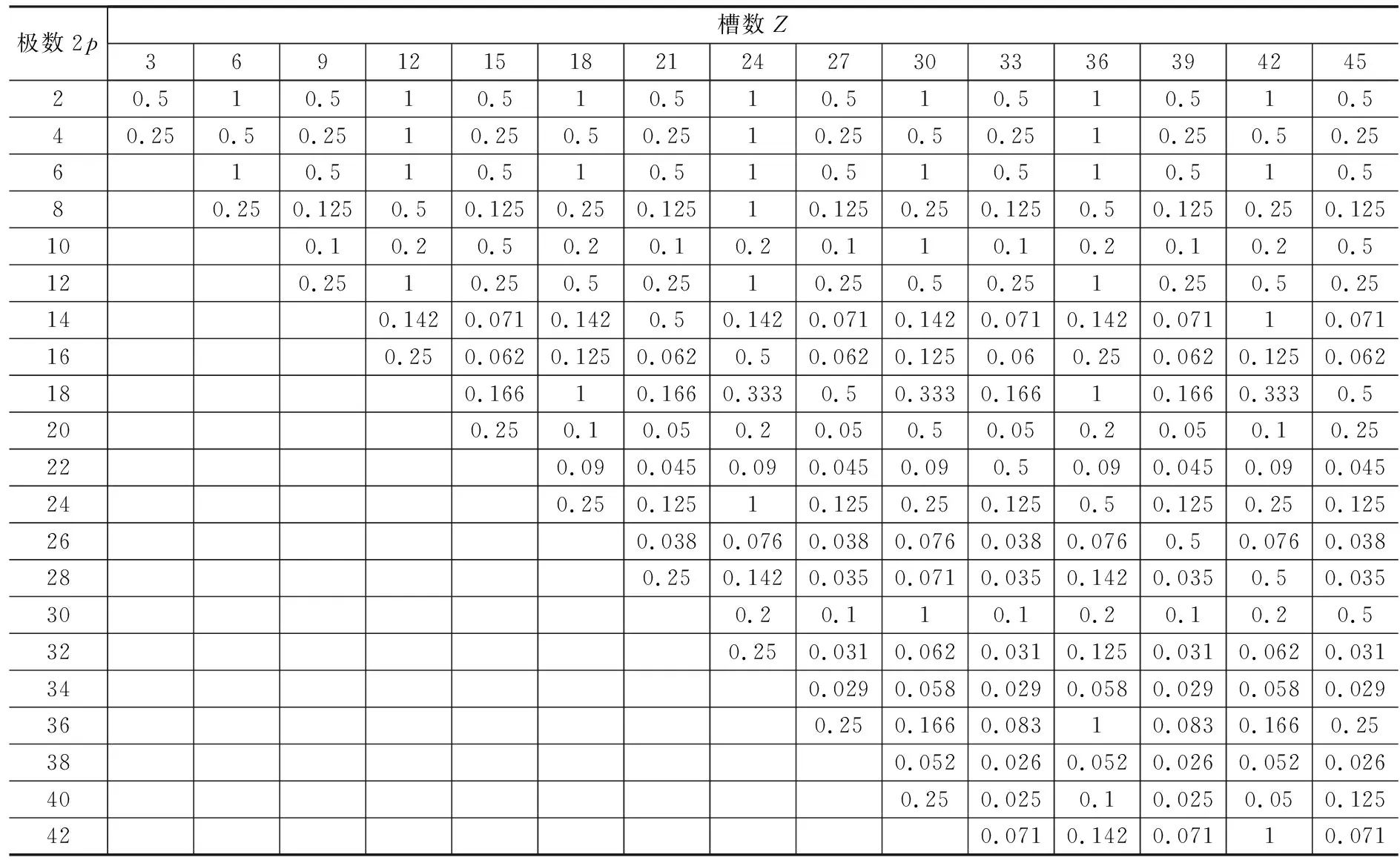
表3 齒槽轉(zhuǎn)矩計算因子KL

整理12槽、4種不同極數(shù)電機的性能及齒槽轉(zhuǎn)矩，如表4所示。

從槽極配合的評判系數(shù)CT、KL看，用KL判斷電機的齒槽轉(zhuǎn)矩大小比CT更確切。

由表4可見，用CT評價電機齒槽轉(zhuǎn)矩評價因子的等級，12槽10極、12槽14極的齒槽轉(zhuǎn)矩是同一個等級，但是12槽14極的齒槽轉(zhuǎn)矩比12槽10極的齒槽轉(zhuǎn)矩更小。同樣的電機體積，電機極數(shù)多，電機的最大輸出功率就小，因此，在確保電機達到最大輸出功率的前提下，可以采用同一CT等級的極數(shù)多的電機結(jié)構(gòu)，從而達到削弱電機齒槽轉(zhuǎn)矩的目的。這也是選取電機槽極配比的方法之一。

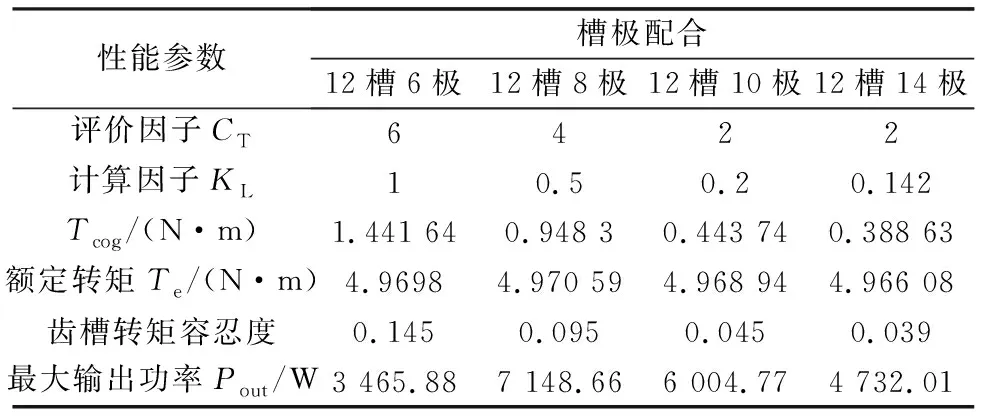
表4 12槽4種極數(shù)的電機性能計算及齒槽轉(zhuǎn)矩的變化

2.9 齒槽轉(zhuǎn)矩峰值的概念

電機齒槽轉(zhuǎn)矩是用峰值考核的，有些地方電機的齒槽轉(zhuǎn)矩用峰峰值表示，稱為齒槽轉(zhuǎn)矩的脈動值，這與電機齒槽轉(zhuǎn)矩大小的評價有關(guān)，讀者務(wù)必注意。

如表5所示，從Maxwell-RMxprt計算中看，12槽10極電機的齒槽轉(zhuǎn)矩為0.443 743N·m。

表5 12槽10極的齒槽轉(zhuǎn)矩計算值

如圖8所示，從RMxprt的電機齒槽轉(zhuǎn)矩的計算曲線看，其峰值為887.486/2=443.743 mN·m。

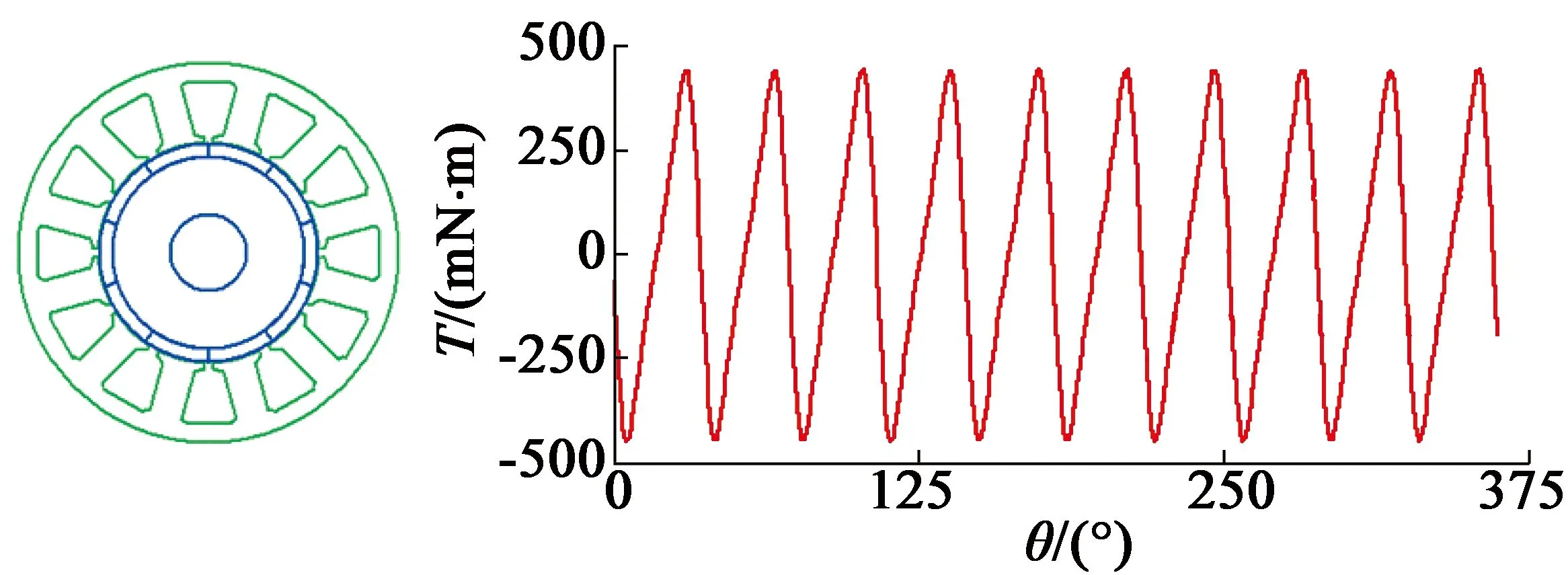
圖8 RMxprt計算的12槽10極齒槽轉(zhuǎn)矩曲線

如圖9所示，從Maxwell 2D場計算看，電機的齒槽轉(zhuǎn)矩887.48/2=443.7 mN·m。

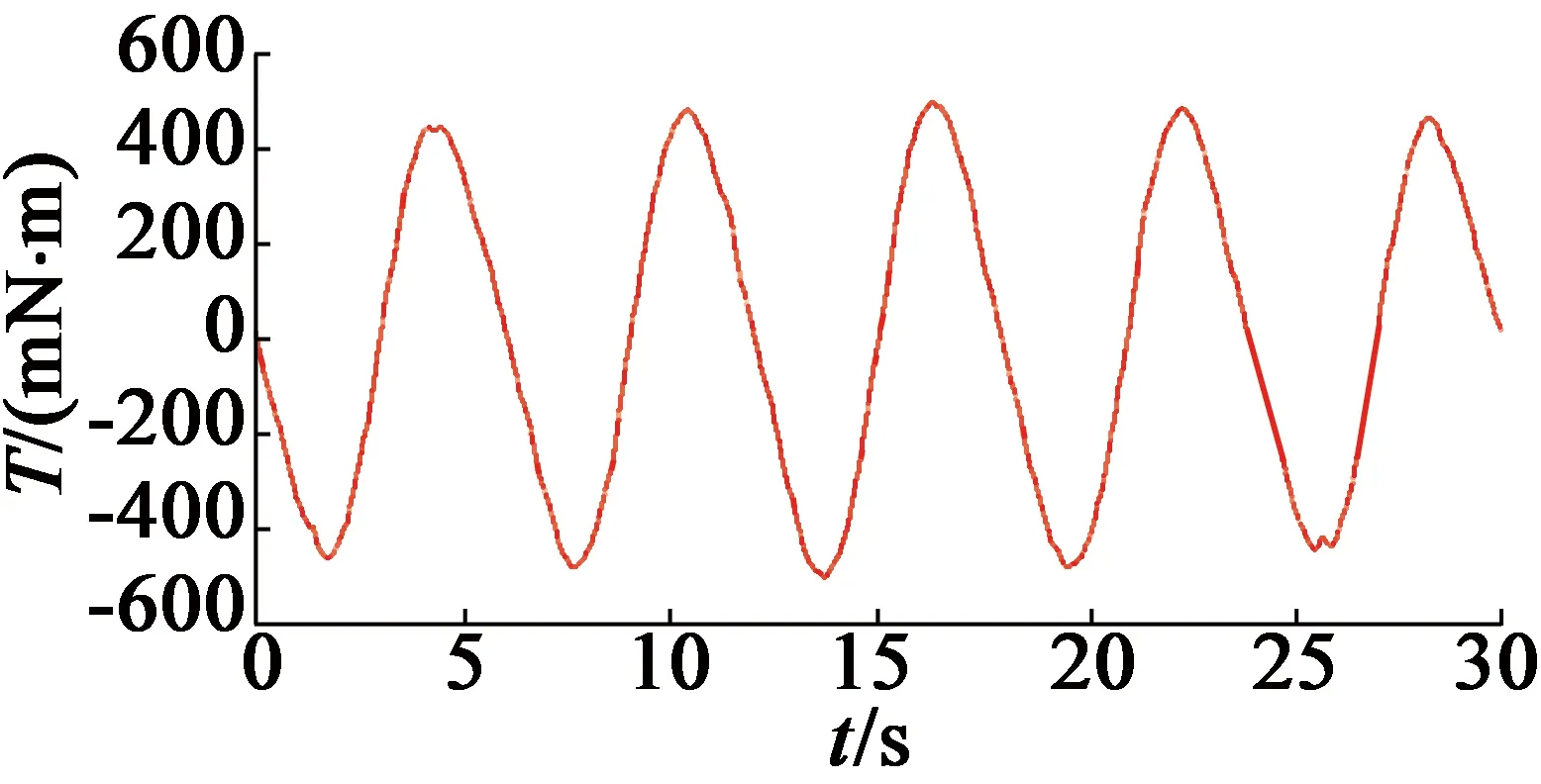
圖9 Maxwell 2D計算的12槽10極瞬態(tài)齒槽轉(zhuǎn)矩曲線

可見，用RMxprt計算的電機齒槽轉(zhuǎn)矩為0.443 743 N·m，電機的齒槽轉(zhuǎn)矩曲線上求得的齒槽轉(zhuǎn)矩也是443.743 mN·m，換算單位后數(shù)值一致。用Maxwell 2D場分析，求取電機瞬態(tài)齒槽轉(zhuǎn)矩，去掉電機起動時的波動，在電機穩(wěn)態(tài)時的電機轉(zhuǎn)矩波動的峰-峰值為1 N·m, 則峰值1 000/2=500 mN·m，與RMxprt計算的齒槽轉(zhuǎn)矩相近。因此，可以認為RMxprt計算的電機齒槽轉(zhuǎn)矩和用Maxwell 2D計算的結(jié)果是一致的。

2.10 齒槽轉(zhuǎn)矩的容忍度

電機齒槽轉(zhuǎn)矩的大小不會影響電機的機械特性，但是電機齒槽轉(zhuǎn)矩大，電機轉(zhuǎn)矩波動就會大。

定義電機的齒槽轉(zhuǎn)矩(峰值)與電機的額定轉(zhuǎn)矩之比為電機齒槽轉(zhuǎn)矩的容忍度。一般，電機的齒槽轉(zhuǎn)矩在額定轉(zhuǎn)矩的1%～2%之內(nèi)，那么就認為電機的齒槽轉(zhuǎn)矩可以容忍。作者設(shè)計時，電機的齒槽轉(zhuǎn)矩容忍度在1%左右。

2.11 同一槽極配合，不同轉(zhuǎn)子形式的齒槽轉(zhuǎn)矩

同一槽極配合，不同轉(zhuǎn)子形式的齒槽轉(zhuǎn)矩是不同的。轉(zhuǎn)子結(jié)構(gòu)形式主要分兩大類：表貼式和內(nèi)嵌式，上面分析主要是依表貼式轉(zhuǎn)子結(jié)構(gòu)，實際同一評價因子CT，同一定子，轉(zhuǎn)子結(jié)構(gòu)不同，其齒槽轉(zhuǎn)矩也不同的。以12槽8極電機為例(CT=4)，其轉(zhuǎn)子結(jié)構(gòu)如圖10所示，轉(zhuǎn)矩比較如表6所示。

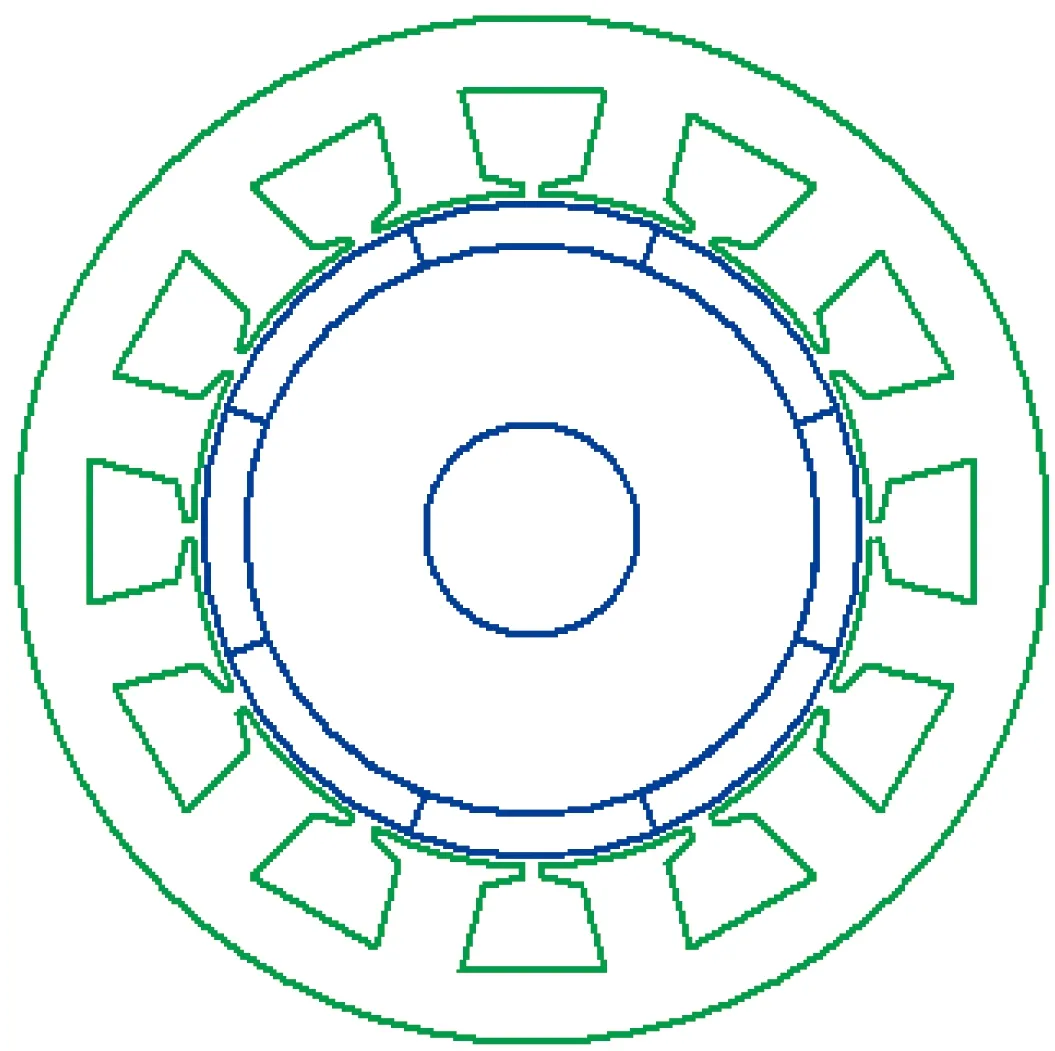
(a) 表貼式

(b) 內(nèi)嵌式

表6 兩種轉(zhuǎn)子齒槽轉(zhuǎn)矩比較

電機齒槽轉(zhuǎn)矩與電機繞組匝數(shù)無關(guān)，與電機運行性能無關(guān)，齒槽轉(zhuǎn)矩在電機不通電狀態(tài)就存在。12槽8極的電機在直極、直槽情況下，內(nèi)嵌式轉(zhuǎn)子的齒槽轉(zhuǎn)矩比表貼式的小一半。

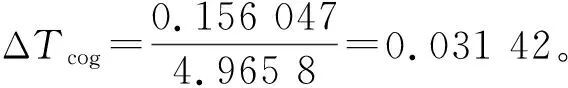
圖11 內(nèi)嵌式轉(zhuǎn)子12槽10極電機的齒槽轉(zhuǎn)矩

內(nèi)嵌式12槽10極電機的齒槽轉(zhuǎn)矩僅是表貼式12槽8極(同心圓磁鋼)的齒槽轉(zhuǎn)矩的0.16倍。

(未完待續(xù))