雙層稀疏組Lasso高分辨SAR結構特征增強成像

楊 磊, 李慧娟, 黃 博, 劉 偉, 李埔丞

(1. 中國民航大學天津市智能信號與圖像處理重點實驗室, 天津 300300; 2. 中國工程物理研究院電子工程研究所, 四川 綿陽 621999)

0 引 言

合成孔徑雷達(synthtic aperture radar, SAR)屬于微波成像雷達,它通過有限尺寸的物理天線形成大的長的虛擬孔徑,從而實現對地面場景的高分辨率成像,其中雷達系統的分辨單元可遠小于目標尺寸,因此能夠獲得包含有細節目標結構信息的雷達圖像,從而有效提高目標的特征分析與自動識別精度[1]。由于實現高分辨SAR成像需要接收并處理寬帶雷達信號,這意味著傳統基于香農-奈奎斯特定理的采樣方法所導致的雷達大數據量會令存儲和傳輸系統不堪重負[2]。2006年,Donoho基于信號逼近等概念提出壓縮感知(compressive sensing, CS)理論[3],該理論指出任何變換域的稀疏信號或可壓縮信號在低維空間上的少量隨機線性投影所得的稀疏解已足夠實現信號重構。這一新型的采樣方法突破了瑞利分辨率的限制,使得確定采樣速率的不再是帶寬,而是信號的結構內容,從而有效降低采樣頻率以及數據處理與存儲帶來的成本。這一發現為信號處理領域帶來革命性影響,同時也極大推動了SAR稀疏特征增強領域的蓬勃發展,各種基于稀疏表示以獲得穩健SAR目標識別與信號恢復的壓縮感知類算法層出不窮[4-6],由于此類算法降低了對圖像預處理的要求,且能夠擁有比傳統方法更高的精度,因此被廣泛應用于多種雷達成像模式,如SAR[4]、SAR地面動目標成像(SAR ground moving target imaging, SAR-GMTIm)[5]和逆SAR(inverse SAR, ISAR)成像[6]。

常見的凸優化類壓縮感知重構算法有基追蹤(basis pursuit, BP)法[7]、最小角度回歸(least angle regression, LARS)法[8]等。這些算法已經廣泛使用,但多變量協同能力差,并且多適用于小規模和低維度數據處理,面對SAR高維特征數據時,其運算復雜度將會指數級上升。針對這一問題,Boyd等人[9]于2011年提出適合大規模分布式約束凸優化問題的交替方向乘子法(alternating direction multiplier method, ADMM)。該方法結合了對偶分解法的可分解性和增廣拉格朗日乘子(augmented Lagrange multipliers, ALM)法的良好上界收斂屬性,通過“分解-調和”過程,首先將初始的全局問題分解成局部的子問題,以此降低全局問題的計算難度,然后采取各個擊破的方式,分別解決每個子問題,最后進行調和過程,即將局部子問題的解進行調和,繼而得到原問題的全局最優解。

這樣的ADMM框架有效降低了原問題的求解難度,大大提高了運算效率,同時在統計學、機器學習和雷達信號處理等多個領域得到廣泛應用[10]。其中,信號處理領域最常見的應用是通過ADMM算法求解1正則化線性回歸(簡稱為Lasso)模型,由于ADMM框架可以自然地將Lasso模型中非平滑的1懲罰項和平滑的最小二乘損失項分離開來,因此基于Lasso的ADMM算法在應用于SAR稀疏特征增強成像時具有良好的穩健性與有效性[11]。但Lasso模型在實際的SAR圖像重構中存在一定的限制,比如SAR圖像中通常會存在同一類型的區域特征信息,這些信息會自然形成一組,若能研究一種Lasso模型的擴展版本,對這類信息進行利用,則SAR圖像重建結果的精度會得到很大改善,因此有必要研究構建一種結構稀疏模型,能夠在SAR稀疏特征增強的同時實現結構特征增強,這將大大提升SAR成像的質量。

Yuan等人利用組結構先驗信息提出組Lasso(Group Lasso)模型[12],將1范數正則化項擴展到具有更為復雜的1/F混合范數正則化約束項。該模型通過人為預先設定分組,實現變量在組水平上的稀疏,即同一個組變量的回歸系數同時為0或不為0的組間稀疏,有效改進了Lasso處理組數據時的缺點。然而,Group Lasso模型在實際應用中也有一定缺陷,比如該模型雖能有效剔除SAR回波數據中不重要的組,卻只能實現組間稀疏,無法對組內信息也進行稀疏處理,這導致該模型在實際SAR稀疏信號恢復成像中靈活性較低。因此本文提出一種有效應用于SAR回波信號重建,基于雙層稀疏Group Lasso ADMM(sparse Group Lasso-ADMM, SGL-ADMM)算法,該算法可通過求得1范數與1/F混合范數的正則化近端閉合解,同時實現組間稀疏和組內稀疏與平滑處理,可以有效提升傳統SAR成像的精度。

本文首先推導得出SAR、SAR-GMTIm、ISAR 3種模式回波信號模型的解析表達式,繼而構建出對應的通用信號模型,利用所提算法對該回波信號模型進行求解。具體來說,SGL-ADMM算法首先針對含最小二乘項的子問題引入嶺回歸求得其解析解,再分別推導得出1/F混合范數及1范數對應的近端算子,并利用“分解-調和”的思想對兩種近端算子及其對應的對偶變量進行并行運算,然后利用高斯-賽德爾思想不斷在SGL-ADMM框架中進行對偶迭代,從而實現對SAR回波復數據的稀疏與結構特征聯合增強。本文實驗驗證分別選用3種SAR模式的仿真數據與實測數據,將所提SGL-ADMM算法與傳統基于Lasso和Group Lasso的ADMM算法進行定性的對比實驗,并采用相變圖(phase transition diagram,PTD)定量分析SGL-ADMM的信號/特征恢復性能,進而驗證了本文所提SGL-ADMM算法應用于SAR成像恢復的可行性和優越性。

1 回波信號模型

本文首先分別推導SAR、SAR-GMTIm和ISAR的數據域回波信號表達式,進而提出同時適用于這3種模式的雷達回波信號通用模型。圖1和圖2中分別給出SAR、SAR-GMTIm和ISAR的成像幾何模型。3種模式均利用雷達與目標之間相對運動形成的虛擬合成孔徑來實現多脈沖回波的相干積累[13],從而實現方位向的高分辨率,并通過載機或地基的雷達天線發射大帶寬和時寬的線性調頻(linear frequency modulation, LFM)信號來保證雷達距離向的高分辨率,再利用相應的SAR成像算法實現對場景目標的高分辨成像。

圖1 SAR、SAR-GMTIm模式數據采集幾何模型Fig.1 Geometric model of SAR and SAR-GMTIm data acquisition

如圖1所示,以點O為原點建立空間直角坐標系O-XYZ。SAR平臺以速度v按預定航線沿坐標系X軸方向(即方位向)飛行。在數據采集過程中,雷達工作在側視聚束模式下,波束中心指向場景中心Oc。

為實現在靜止場景中檢測運動目標響應并完成對運動目標的重聚焦成像從而采用多通道天線,設第n通道等效天線相位中心(antenna phase center, APC)為

qn(t)=q0(t)+dn

(1)

式中，q0(t)為參考通道位置矢量;等效APC沿航線均勻分布且間距為d;dn為參考通道到第n通道的空間矢量;t為方位向慢時間變量。雷達信號的收發模式是n個通道的等效APC同時收發信號。

1.1 SAR模式

設載機到場景中心的斜距距離參考矢量為R0=R0r,其中r為斜距向單位矢量。則靜止目標距離SAR平臺的實時斜距為Rs(t)=|R0+rs-q0(t)|,將其在參考斜距|R0-q0(t)|處進行泰勒展開可得

(2)

式中，rs為靜止散射點P相對于場景中心Oc的偏移矢量;O(t)是在參考斜距|R0-q0(t)|處的2階及以上展開項,在遠場假設下可以忽略不計。根據雷達原理,載機發射的LFM信號經過式(2)所示的距離歷程后,對接收到的回波數據進行距離向壓縮、方位向解線性調頻LFM技術處理和極坐標形成算法(polar formation algorithm, PFA)插值處理[5],可得SAR模式下的數據域為

(3)

式中，地面靜止的第s個散射點的初始位置為(xs,rs);sinc函數為第s個散射點的距離向包絡;exp函數為方位線性相位項;λ為雷達系統發射信號波長;t′為插值后的慢時間變量;cn為雜波和噪聲。

1.2 SAR-GMTIm模式

在SAR-GMTIm模式下,如果考慮到地面成像場景中存在運動目標,假設其勻速速度為vt,可分解為方位向和斜距向的速度(vx,vr),則SAR地面動目標成像模式中運動目標距離載機平臺的斜距為

(4)

式中，rm為運動目標相對于場景中心Oc的位置偏移矢量。式(2)與式(4)均為實時斜距在參考斜距|R0-q0(t)|處的泰勒展開,區別在于式(2)針對地面靜止目標并展開至一階,而式(4)是針對動目標計算斜距,假設運動目標勻速直線運動情況下,考慮到其速度會造成2階調制,因此式(4)中泰勒展開至2階,從而可以得到式(4)所示SAR-GMTIm模式下的斜距表達式。設第m個運動目標的初始位置為(xm,rm),考慮到對地面運動目標成像時,靜止場景回波即雜波的影響,可能造成運動目標檢測及成像性能降低,因此結合沿航向多通道SAR系統回波,將第i通道回波與參考通道回波相減,則可實現雜波相消[14-15],從而得到SAR-GMTIm模式下數據域表達式為

(5)

(6)

1.3 ISAR模式

ISAR成像模式理想轉臺幾何模型如圖2所示。

圖2 ISAR模式數據采集幾何模型Fig.2 Geometric model of ISAR mode data acquisition

假設進行平動運動補償后,雷達相對靜止而目標僅存在相對于參考點的轉動分量。設雷達位于C點,飛機中心為O,在機身內建立空間坐標系O-XY,其中J點是飛機上任意一點,其位置為(xs,rs),與坐標軸夾角為θ,相對中心O的偏移矢量為rp=OE+EJ。目標以角速度ω圍繞自身做旋轉運動,在此過程中雷達波束持續覆蓋目標。根據矢量相加可得散射點和雷達的距離:

Rp(t)=R0+|rp|=R0+rscos(θ(t))+xssin(θ(t))

(7)

當ISAR成像積累時間較短,θ較小時,可近似認為目標在勻速旋轉,即滿足等式θ(t)=ωt,sin(ωt)≈ωt,cos(ωt)≈1。因此,可得ISAR模式下數據域表達式為

(8)

式中，As為散射點的后向散射能量值。

通過觀察如式(3)、式(5)和式(8)所示的3種成像模式回波信號模型,可見3種模型的共同點是均有距離向包絡sinc函數和方位向的線性相位,并且都存在雜波和噪聲項,因此在經歷如距離壓縮、雜波相消等一系列過程的處理后,3種模式的回波信號模型可以通過統一的矩陣形式建立:

Y=AX+W

(9)

A0=[a[ζd(1)],a[ζd(2)],…,a[ζd(n)]],
a[ζd(n)]=[e-j2πζd(n)t1,e-j2πζd(n)t2,…,e-j2πζd(n)tN]T

(10)

在SAR-GMTIm模式下時,A是二階參數化傅里葉字典，即

(11)

2 雙層稀疏組Lasso成像算法

求解式(9)所示的回波模型是典型的圖像不適定問題，而解決不適定性的有效途徑則是在數據壓縮感知處理中引入關于目標解的先驗信息,因此創建目標結果的先驗模型對于實現高分辨雷達成像至關重要。近年來,熱門的正則化幾何模型被人們廣泛應用于雷達信號重建,正則化方法的本質是采用一組與原不適定問題相鄰近的適定問題的解,來無限逼近原問題的解,并給模型添加規則限制用以約束要優化的參數,防止過擬合,最經典的便是Tibshirani[17]提出的Lasso模型

(12)

式中，‖·‖F為Frobenius范數;‖·‖1為1范數;ρ>0為正則化參數。右側括號中第1項為最小二乘項,即數據保真項,用以衡量雷達恢復信號與原含噪信號的逼近程度；右側括號中第2項為懲罰項,用以添加SAR圖像中強散射點具有的稀疏先驗信息約束。然而，SAR的實際成像場景龐大,地物信息豐富,場景中散射點的強度不均且各種散射特征極復雜,高分辨成像雖然為目標的精細特征提取提供了有利的條件,但Lasso模型僅可單純地增強成像目標的稀疏特征,雖能有效消除背景噪聲與雜波,卻會同時造成目標弱散射特征的丟失,使得精細的結構特征在成像恢復中難以保留,從而降低了高分辨成像特征提取優勢。事實上，雷達信號中存在相似散射點可以自然地歸為一組,形成連續性結構,只考慮稀疏特征則會導致無法保留目標的連續性,使得在抑噪的同時將部分有用信息也一并去除,因此如何在SAR成像中增強散射點稀疏特征的同時增強目標的結構特征變得尤為重要。針對Lasso模型的這一缺點,本文提出可實現雙層稀疏SGL模型，表示為

(13)

式中，Xi表示矩陣X的第i個塊結構(組),且i=1,2，…，L。λ1和λ2分別為1范數和F,1范數對應的正則化參數,用以調節恢復中圖像的稀疏度和結構平滑度。當L=1時，相當于X只有一個組,即不考慮塊結構特征,此時式(13)將變為式(12)的Lasso問題。當λ1=0時,該模型則變為Group Lasso形式,不再具有組內稀疏性。當SGL模型應用于SAR成像時,第2項1范數可對雷達成像場景的每個分辨單元回波數據進行稀疏表征,即該懲罰項可實現組內稀疏。第3項是F,1范數,該項首先在第2項Laplace先驗的基礎上增加了高斯先驗,使得SAR場景中散射點的塊結構內部具有平滑特性,即實現組內平滑。對每個組利用Frobenius范數結構平滑后,進一步添加對L組加總求和約束,相當于在組水平上進行稀疏,區別于1范數對每個像素稀疏,該組合盡可能選出更少的組,即可實現組間稀疏,從而共同組成了具有結構懲罰特性的F,1范數,這樣的雙層SGL模型在SAR成像中可以在剔除不需要的組的同時具有組內特征稀疏的靈活性,可更加有效地保留有用結構信息,去除背景噪聲。另外,在引入塊結構特征先驗信息的過程中,本文采用計算歐式距離的方法對雷達回波復數據進行分組,通過設置一定閾值,將區域聚類特征信息歸類,再利用F,1范數平滑與稀疏,從而有效保留目標中的有用信息。

綜上所述,SGL模型可實現SAR多特征聯合增強,因此選擇適合的算法求解該模型是關鍵,但傳統的SAR成像算法協調多特征的能力較差,容易顧此失彼,不能將SGL模型的多特征增強優勢發揮出來,造成最終成像效果不盡人意。本文提出的SGL-ADMM算法引入的ADMM優化框架結合了對偶分解法和ALM法的優點,其優勢便在于利用分解-調和思想,將復雜難解的全局大問題分解為多個較易求解的局部子問題,在實現分布式優化的同時可調和全局問題,實現結構特征與稀疏特征的聯合增強時的最佳協調,且具有優越的收斂性和穩健性。SGL-ADMM算法可由式(13)轉化為如下約束性優化問題:

min [f(X)+g(Z)]
s.t.BX+DZ=0

(14)

(15)

g(Z)=g1(Z1)+g2(Z2)=

(16)

進而可得式(14)的增廣拉格朗日形式為

(17)

式中，γ為拉格朗日乘子系數;[·]H表示矩陣的共軛轉置;U為對偶更新變量。式(17)帶有二次懲罰項增廣拉格朗日函數的對偶上升方法,即為交替方向多乘子法中的多乘子與多分裂變量的來源。此時,利用SGL-ADMM算法求解式(17)問題,可得

(18)

式中，S1=(1/γ)U1和S2=(1/γ)U2為歸一化對偶變量(或縮放變量)。將式(16)代入迭代過程,可得

(19)

式中，上標k表示矩陣的迭代次數。算法中第1步迭代為求解原變量X,是典型的最小二乘問題,相當于求解嶺回歸問題。第2步是針對分裂變量Z1的1范數正則優化,通過求解1范數對應的近端算子來實現組內稀疏。第3步是Z1相應的對偶變量更新過程。第4步為針對分裂變量Z2的F范數正則優化,可實現組內平滑和稀疏。第5步為Z2相應的對偶變量更新過程。由式(19)可見SGL-ADMM算法迭代過程中變量X、Z1和Z2是相互交替進行更新,因此稱之為交替方向。

2.1 原變量X更新

對式(19)第1步X的聯合最小化求解并更新,相當于嶺回歸問題,其目標函數為

(20)

可見目標函數為凸函數,則對其求導可得

(21)

令導數為0，則X的解為

Xk+1=(AHA+γI)-1[AHY-BH(DZk-Sk)]=

(22)

2.2 分裂變量Z1更新

(23)

式中，proxλ1/γ(·)表示函數的近端算子,此處表示1范數對應的軟閾值算子。針對SAR回波的復數性質,對矩陣Z進行復數分解,并且分別對實數與復數部分求導,可得復數軟閾值算子為

(24)

(25)

2.3 分裂變量Z2更新

(26)

對第i組的每個變量求次梯度(近端算子)可得

(27)

(28)

基于SGL罰高斯回歸模型的ADMM算法如下所示。

基于SGL罰高斯回歸模型的ADMM算法步驟 1 初始化,令k=0,X0,Z0,S0;步驟 2 設定迭代次數與目標精度,若停止準則不滿足,進行循環;步驟 3 根據式(22)更新X變量,即Xk+1=(AHA+γI)-nd 步驟 6 若不滿足停止準則,繼續步驟3～步驟5,若滿足停止準則,跳出循環;步驟 7 停止迭代,輸出X。

本文提出的SGL-ADMM算法與傳統基于Lasso模型的ADMM算法主要區別是，在SAR回波復數據處理中引入了能夠實現SAR目標結構特征增強的分裂變量Z2(步驟5),并且同時保留了傳統ADMM算法中能夠實現稀疏特征增強性能的分裂變量Z1(步驟4),因此最后步驟7中輸出的是稀疏特征與結構特征聯合增強后的圖像X。SGL-ADMM算法首先引入稀疏先驗,通過推導1范數對應的近端算子,即復數軟閾值算子來得到稀疏閉合解。然后利用SAR數據中的L組先驗特征信息來引入F范數,并通過循環迭代L次來求得結構閉合解,達到SAR數據全局平滑效果,從而實現SAR結構特征增強。基于這樣的并行優化框架,SGL-ADMM算法相對于傳統SAR成像算法可以有效提升精度和運算速率。

3 實驗驗證

為了驗證所提SGL-ADMM算法用于SAR、SAR-GMTIm以及ISAR 3種模式進行高分辨成像時的可行性以及多特征增強效果等性能,本文首先基于仿真轉臺模型數據利用Lasso-ADMM算法、Group Lasso-ADMM算法以及所提SGL-ADMM算法進行3種模式下的成像定性對比,再應用美國Sandia實驗室公布的實測SAR復數據圖像和Yak-42運輸機實測ISAR數據以及Gotcha雷達動目標數據集這多組實測數據分別進行3種算法的定性成像對比實驗,最后將仿真轉臺模型的蒙特卡羅數據用于相變熱力圖成像恢復實驗來進行性能評估,用以定量對比分析3種算法的回波信號恢復性能。從而有效驗證了所提SGL-ADMM算法相較傳統算法的優越稀疏與結構特征恢復性能。

3.1 仿真實驗

本文首先采用一組仿真轉臺模型數據成像實驗來驗證所提SGL-ADMM算法的優越性能。為了驗證SGL-ADMM算法相較傳統算法在雷達回波信號連續結構特征方面的恢復性能,本實驗設置仿真合成的轉臺模型數據,并假設散射體位于場景距離向和方位向的十字交叉區域,其中目標與雷達相距50 km且無平移運動,具體的雷達參數如表1所示。

表1 仿真實驗參數設置

圖3(a)所示為無噪聲且無降采樣時的轉臺模型參考恢復圖像,圖中十字區域內共有57個散射點,并且各個點的強度服從復高斯分布,精度為1/5,是方差的倒數,均值為2。整個目標位于場景中心并且具有明顯的強連續性結構。圖3(b)為對圖3(a)進行降采樣與加噪聲處理后的成像結果,其中降采樣率為0.7,加入的高斯白噪聲為10 dB。圖3(c)為基于傳統Lasso模型的ADMM算法對圖3(b)的重建成像,由于Lasso-ADMM算法僅有稀疏先驗,因此盡管成像結果抑噪效果明顯,但目標的結構特征已經幾乎喪失,十字輪廓也未重建。圖3(d)為基于Group Lasso模型的ADMM算法成像效果,該模型同時具有組間稀疏與組內結構平滑能力,因此相較圖3(c)該算法在結構特征方面增強明顯,鑒于ADMM算法的調和性能,Group Lasso -ADMM算法在結構特征保留的同時,背景的去噪稀疏能力也較強。但該算法仍有不足之處,首先散射點附近仍有少許噪聲未被抑制,其次參考恢復結果中的散射點成像結果強度差異性較大,而Group Lasso -ADMM算法并未將圖3(a)所示不同點的散射強度精確地恢復。圖3(e)為本文所提SGL-ADMM算法恢復結果,該算法在Group Lasso -ADMM算法基礎上增加了組內稀疏性能,因此可以完整恢復目標散射強度,并且相較Lasso -ADMM與Group Lasso -ADMM算法,背景稀疏特征與目標結構特征聯合增強效果十分顯著。對比本文所提方法的恢復精度(歸一化均方誤差(normalized mean square error,NMSE)為0.31)與Lasso(NMSE為6.21)和Group Lasso(NMSE為2.44)可見,該方法具有更高的成像恢復精度。

圖3 ISAR仿真數據不同算法成像結果Fig.3 ISAR simulation data imaging results of different algorithms

3.2 SAR實測數據成像恢復實驗

實驗應用美國Sandia實驗室公布的SAR實測復數據圖像來驗證SGL-ADMM算法成像效果。圖4目標場景為綠化帶與馬路的SAR成像結果。

圖4 SAR實測復數據不同算法成像結果Fig.4 SAR imaging results of different algorithms based on complex real data

其中圖4(a)為經過降采樣與加噪聲處理后的SAR結果,降采樣率為0.5,加入的高斯白噪聲為10 dB。圖4(b)為Lasso-ADMM算法的恢復成像效果,此時綠化帶內像素點已經較為分散稀疏,且未形成連續結構,與此同時背景噪聲也未完全抑制,可知如若進一步把1范數對應的正則化參數ρ增大,雖然會令噪聲去除干凈,但綠化帶內部塊結構的像素點會更加稀疏,甚至喪失邊緣結構特征。圖4(c)為Group Lasso-ADMM算法的SAR成像結果,可見相較圖4(a),散射體組內平滑效果明顯,塊結構特征得以增強,但馬路背景仍存在噪聲。圖4(d)為SGL-ADMM算法處理后圖像,目標結構特征完整保留,地物輪廓特征清晰,且抑噪能力強,成像結果對比度最高。

3.3 ISAR實測數據成像恢復實驗

本組實驗采用Yak-42實測圖像進一步驗證SGL-ADMM算法的成像效果。圖5(a)為降采樣率0.7以及5 dB高斯白噪聲處理后圖像。圖5(b)為利用Lasso-ADMM算法實現的ISAR成像,由于未考慮結構先驗,飛機頭部與機身上部斷開,左邊機翼中部亦斷開,右邊機翼則與機身下部僅有一絲連續,而此時噪聲仍未徹底去除,當調節正則化參數ρ使抑噪性增強時,目標的結構特征已喪失很多。圖5(c)為Group Lasso-ADMM算法處理后的ISAR圖像,相較圖5(b)該算法在背景去噪較為干凈的同時飛機結構特征也保留較為完整。圖5(d)為SGL-ADMM算法處理后的ISAR圖像,明顯飛機內部結構非常飽滿,機身中部無空白,飛機輪廓清晰,由于機頭與機身本就是同一類塊結構特征,因此在恢復后也本應具有完全的連續性,SGL-ADMM算法在完整恢復飛機結構特征的同時將背景噪聲也完全抑制,由此可見所提算法對于稀疏與結構兩種特征的相互調和能力較強,恢復性能較好。

3.4 SAR-GMTIm實測數據成像恢復實驗

在本組SAR動目標實驗中,通過應用Gotcha數據集[18],對所提算法和基于Lasso、Group Lasso的ADMM方法進行定性和定量對比實驗。圖6(a)所示為在動目標數據集中選出的一部分地面動目標數據,鑒于車輛在運動時本身存在一定的速度,使得最終的SAR-GMTI成像結果散焦嚴重,并且相對于實際的位置,成像后的車輛位置發生了一定的偏移。圖6(b)為圖6(a)圖像的擴大區域,以此更清晰地顯示出觀測目標。

圖5 ISAR實測復數據不同算法成像結果Fig.5 ISAR imaging results of different algorithms based on complex real data

圖6 Gotcha GMTI實測數據成像結果Fig.6 Gotcha GMTI real data imaging results

圖7(a)為經過多通道雜波相消與LVD時頻表示后,采用傳統的匹配濾波器組法進行的聚焦成像,可見雖然車輛有聚焦效果,但背景雜波噪聲嚴重,成像效果不佳。圖7(b)為Lasso -ADMM算法成像結果,圖像的聚焦性能與稀疏性能均顯著提高,但不足的是目標車輛的輪廓結構未完整恢復,車頭部分幾乎未恢復。同時本實驗進行定量分析來衡量成像的效果,圖7(b)中其熵為4.619 2,目標雜波比為32.179 9。熵值愈小則聚焦愈強[19],目標雜波比愈大則目標散射強度愈強[20]。圖7(c)為Group Lasso -ADMM算法成像結果,其熵為4.403 6，目標雜波比為32.509 7,可見相較圖7(b),該算法在結構特征增強效果有所改善,但目標整體結構仍有缺陷。圖7(d)為SGL-ADMM算法處理后圖像,其熵為4.002 5,目標雜波比為33.034,相較另外兩種算法,本文所提算法重建圖像的圖像熵最小,目標雜波比最大,因此圖像的稀疏特征、結構特征以及聚焦特征聯合增強效果明顯,并且多特征增強并未使算法運算效率過多降低,其運算耗時一般比傳統ADMM算法多5～10 s。本組SAR-GMTIm實測實驗通過定量與定性分析有效證實了SGL-ADMM算法的優越恢復性能。

圖7 Gotcha GMTI實測數據不同算法成像結果Fig.7 Gotcha GMTI real data imaging results of different algorithms

3.5 相變熱力圖恢復實驗

PTD是由斯坦福大學的Donoho教授提出[21],用于計算和對比各個算法間的重建能力。該定量實驗應用圖3的仿真轉臺數據對Lasso -ADMM、Group Lasso-ADMM以及所提算法進行蒙塔卡羅實驗,并計算在動態參數調節下,各個算法的重建結果相較于圖3(a)的相關程度,從而對比得出本文所提算法的優越恢復性能。圖8所示為固定50%稀疏度下,3種算法的降采樣率(downsampling rate, DSR)-信噪比(signal to noise ratio, SNR)相關度熱力圖,橫軸為DSR,縱軸為SNR。

圖8 不同算法DSR-SNR相關度PTD對比Fig.8 Comparison of different algorithms for DSR-SNR ratio correlation PTD

熱力圖的衡量指標相關系數的計算公式如式(29)所示,圖8中紅色部分顏色越深表示算法成像圖與參考恢復圖的相關系數絕對值|RXXk|越接近1,即相關程度越大,重建結果越好,黃綠藍色漸變部分顏色越深則表示|RXXk|越接近0,重建效果越差。

(29)

式中，cov(·)、E(·)和σ(·)分別為計算信號矩陣的協方差、數學期望與方差。

圖9所示為固定SNR為-5 dB條件下,3種算法的DSR-稀疏度(sparseness, SR)相關度熱力圖,橫軸為DSR,縱軸為SR。

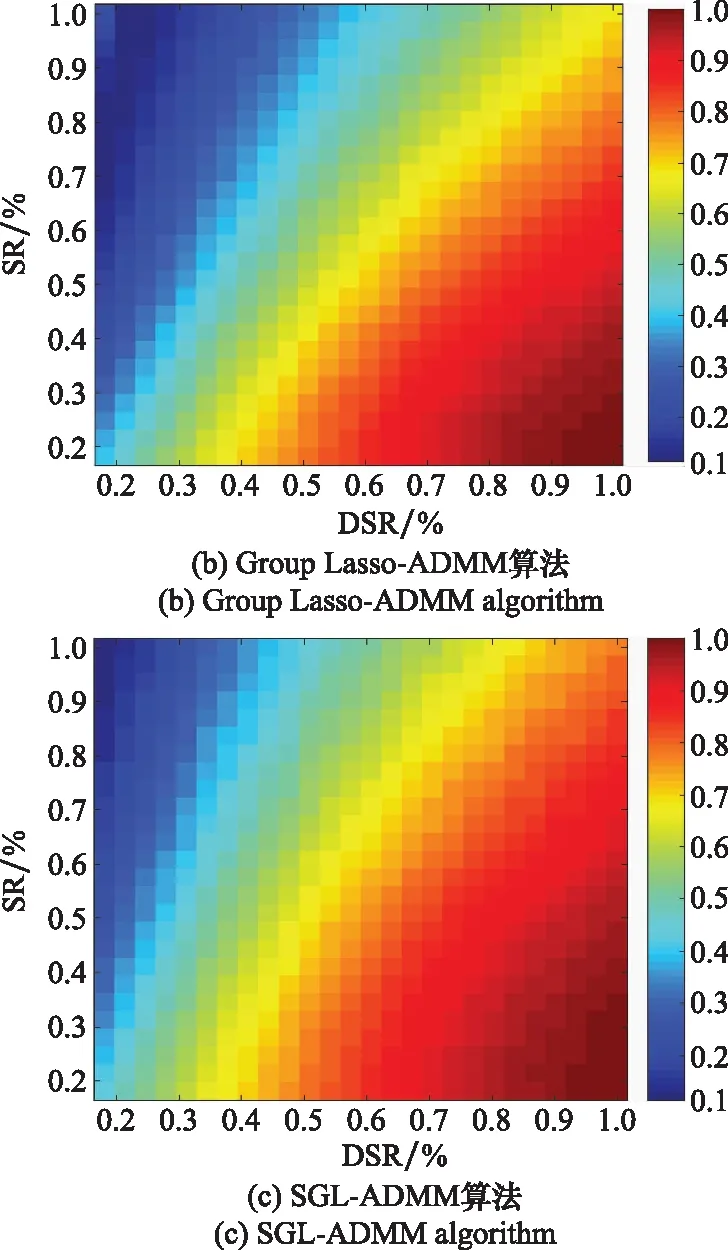
圖9 不同算法DSR-SR相關度PTD對比Fig.9 Comparison of different algorithms for DSR-SR ratio correlation PTD

綜上所述,針對Lasso -ADMM算法、Group Lasso-ADMM算法以及所提SGL-ADMM算法進行的兩組不同參數下的熱力圖對比實驗均顯示SGL-ADMM算法的紅色部分面積大于其他兩種算法,而更大面積的高相關值區域表示算法在不同DSR、SNR和SR環境下的恢復穩健性越高,因此有效驗證了所提算法應用于SAR回波復數據的優越恢復性能。

4 結 論

本文針對僅能實現單一稀疏特征增強的傳統凸優化類算法在SAR成像過程中會使得目標的精細結構特征丟失這一問題,提出能夠同時實現目標稀疏特征與結構特征聯合增強的SGL-ADMM算法。所提算法首先通過在ADMM框架中引入1/F混合范數并推導其對應的近端算子來實現結構特征表征,然后通過推導1范數面向SAR回波復數據的復數軟閾值來實現稀疏特征表征,最后利用SAR、SAR-GMTIm和ISAR 3種模式下的仿真數據和實測數據,對所提算法與Lasso-ADMM算法、Group Lasso-ADMM算法進行定性成像對比,并利用蒙特卡羅相變熱力圖定量分析所提SGL-ADMM算法的成像重建性能,從而有效驗證了該算法卓越的多特征聯合增強能力。然而在實驗過程中,本文發現該算法在對目標構造分組先驗時具有多選擇性和靈活性,因此有必要研究一種最佳的分組方式,如嘗試突破歐式距離限制,采用其他擬合程度更好的距離方式可能會達到更好的效果,使算法成像精度得到進一步提升,這將是后續工作的重點。