基于Sobol敏感性分析的裝備體系保障效能評估

潘 星, 張振宇,2, 張艷梅, 王冉冉

(1. 北京航空航天大學可靠性與系統工程學院, 北京 100191; 2. 中國船舶工業系統工程研究院,北京 100036; 3. 北京電子工程總體研究所, 北京 100854)

0 引 言

現代戰爭勝負不再由單一兵種或者單個武器裝備所決定,而是強調體系化作戰。裝備體系中由于存在著不同類型裝備備件共用、保障組織重合等問題,從而呈現出一體化聯合保障的特點,使得單一裝備的保障不能滿足體系化作戰的需求,需要考慮對整個裝備體系進行保障[1],提高裝備體系保障效能,以遂行一體化作戰任務。

裝備體系保障效能研究源于裝備保障效能的研究。裝備保障效能是裝備保障任務所能達到預期目標的程度[2]。當前裝備保障效能的研究主要集中在國內,基本是沿用系統效能評估方法,主要分為3種。一種是運用系統效能評估ADC(availability, dependability, capability)模型[3]計算保障效能,如將任務可靠度和裝備完好性分別作為可信性和能力指標,提出基于可用度和任務可靠性的飛機保障效能指標[4]。第二種是建立保障效能評估指標體系,再采用綜合評估方法對保障效能指數進行評估,如建立裝備能力-性能-特性指標體系,基于效用函數評估單項指標并采用德爾菲法給定權重的方式來評估裝備保障效能指數[2];建立包括人力資源、設施設備和指揮體系的指標體系,再基于熵、主成分分析、理想解法等方法的組合評估方法對保障效能進行排序[5];建立包含信息效能、決策效能和行動效能的裝備保障指揮效能指標體系,并給出基于圖譜分析方法的評估結果[6]。第三種方法是用裝備保障中單項指標或綜合指標來反映保障效能,如用油料保障能力和油料保障效率來反映航空兵場站油料保障效能[7];用裝備可用度、戰備完好度、訓練完好度和在修數量作為度量裝備運用與保障效能指標[8]。除了以上裝備保障效能研究,還有將裝備保障系統視為保障體系進行研究,如對裝備保障體系進行基于智能體的仿真建模并對其中的關鍵技術進行研究[9];對裝備保障體系分布式保障任務分配進行研究,并進行多主體仿真[10]。以上研究只針對單裝的保障或者保障體系,沒有從裝備體系層面進行保障方面的研究。同時,隨著體系工程方法的出現[11-12],現有研究逐漸延伸到裝備體系,從裝備體系的效能評估[13-14],再到裝備體系可靠性、維修性和保障性的研究[15]。

本文以裝備體系為研究對象,以裝備體系保障為中心對裝備體系保障效能評估方法進行研究。首先進行體系保障能力分析,得出相關的能力指標;然后在Sobol敏感性分析方法的基礎上,以體系可用度為敏感性分析目標,建立了綜合層次分析法(analytic hierarchy process, AHP)、Sobol敏感性分析方法以及冪指數法的裝備體系保障效能指數評估方法;最后通過具體的裝備體系進行案例分析,運用多智能體仿真技術對裝備體系保障效能進行了仿真評估。

1 裝備體系保障能力分析

能力分析是連接裝備體系戰略目標與發展方案的核心環節,用于明確裝備體系完成使命任務所需具備的能力,并確定反映能力的指標和實現能力的具體裝備[16-17]。綜合保障任務作為裝備體系任務之一,主要對裝備體系作戰任務起支持作用,也要從能力層面進行分析,對其分析時一般遵循使命到任務、任務到能力、能力到指標的分解框架[15]。裝備體系的綜合保障任務來源于裝備體系遂行的作戰使命以及各裝備的保障需求,在建立裝備體系保障指標體系時,從裝備保障性的基本定義出發,結合裝備體系作戰特點,提出裝備體系保障能力分析模型，如圖1所示。

圖1 裝備體系保障能力分析模型Fig.1 Analysis model of equipment system of systems support capability

裝備體系保障能力反映的是裝備保障體系或裝備保障系統對裝備體系進行保障的總體能力,其主要分為裝備維修能力、資源補給能力和指揮調度能力,其中裝備維修能力又包括裝備搶修能力和后送維修能力。

(1) 裝備維修能力，指的是裝備維修保障組織/系統使用各種維修方法對裝備進行修復的能力,體現的是恢復裝備規定的技術狀態時相應的裝備維修能力發揮的實際效果,反映了武器裝備故障或損壞后的“再生”程度,裝備維修指標決定了作戰持續時間和持續能力。

(2) 資源補給能力，指的是裝備備件、維修保障資源補給相關方面的能力。資源補給的效率直接決定了保障活動進行的效率,高效的資源補給效率可以為戰場裝備提供充足的保障資源,保證裝備可在戰場進行高強度的連續工作。

(3) 指揮調度能力，指的是控制維修保障活動、協調維修保障組織/系統方面體現的能力,是組織好戰場搶救搶修、協調配置保障資源的關鍵環節。維修保障活動的指揮決策是否得當,將直接影響維修保障任務的成敗和戰爭的勝負。

在對裝備體系進行保障能力分析后,即可根據能力構成來分解相應綜合保障能力指標,作為后續裝備體系保障效能評估的依據。

2 面向體系可用度的敏感性分析

2.1 Sobol敏感性分析法

敏感性分析是裝備體系建設和體系結構優化的重要依據。通過敏感性分析,可計算出哪些指標對效能影響最大,從而分析出武器裝備對體系貢獻程度,進而為裝備體系建設提供指導。

現有敏感性分析方法包括局部敏感性分析方法和全局敏感性分析方法兩類。

(1) 局部敏感性分析方法，是指固定其余輸入變量,只改變被研究的單個輸入變量的數值,以該輸入變量的變化引起輸出的變化作為該變量的敏感性分析結果[18]。這類方法將模型的輸出對輸入進行微分,適合于模型輸入和輸出為線性關系的情況,原理簡單、便于使用,但不適用于對一組輸入進行敏感性分析的情況。

(2) 全局敏感性分析法，可同時對多個因素進行敏感性分析,因素變動范圍可擴展到整個定義域區間,且各因素的變化范圍可以不同且可以實現同時變化[19]。該方法不受模型結構的限制,利用解析或仿真方法可以開展對非線性、非單調模型的研究,可同時變動所有的輸入參數,模型輸入空間更大,分析結果也具有較好的對比性[20]。

裝備體系組成復雜,其效能受諸多因素影響,與局部敏感性分析方法相比,全局敏感性分析更適用于裝備體系的保障效能評估。全局敏感性分析方法中,應用較廣泛的是Sobol指數法[21-22],其核心思想就是基于方差的分解,把函數模型分解為單個參數以及參數之間的組合,通過計算單個輸入參數或輸入參數集的方差對總輸出方差的影響來進行參數的敏感性分析[23-24]。

假設模型Y=f(X),其中X=[x1,x2,…,xi,…,xn],i=1,2,…,n，xi為性能指標或影響因素。如果f(X)的平方是可積的,則可把模型分解為

f1,2,…,n(x1,x1,…,xn)

(1)

(2)

式中,X-i表示不包括Xi的其余變量;EX-i(Y|xi)表示Y的條件數學期望,即xi取多個固定值,每個固定值下其他變量即X-i進行多次取值后的Y的均值;SXi表示Xi的“主效應”指數,描述Xi“獨自”對Y的方差的貢獻,數值在[0,1]內,其值越大表明變量Xi的變動對Y影響越大,即Y對變量Xi的敏感度越大。

2.2 體系可用度

在裝備保障效能的評估中,一般以裝備可用度作為衡量裝備保障的綜合指標,而在體系層面對保障效能進行評估時,不宜以某個或幾個裝備是否可用來衡量體系是否可用,應從裝備體系能力角度對裝備體系具體使命任務進行分析[25-26],并給出最小裝備可用清單,據此可定義體系可用度的概念,并對其進行敏感性分析。

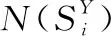
(3)

基于以上體系可用度定義,可將所有裝備體系保障能力指標針對體系可用度進行全局敏感性分析,計算各能力指標的敏感性指標,作為后續裝備體系保障效能冪指數法評估中的權重系數:

(4)

3 基于敏感性分析的保障效能評估

3.1 基于冪指數法的效能評估

冪指數函數式結構簡單,適用于快速評估和宏觀分析,可在裝備指標基礎上進行效能評估[27]。冪指數法常用于裝備效能評估中,對于裝備體系效能評估也可使用。冪指數法認為裝備效能與性能指標之間存在函數關系,性能指標用向量X=[x1,x2,…,xn]表示,裝備效能用E表示,則有

E=F(X)

(5)

裝備效能E與性能指標X存在函數關系應滿足如下假設和規律。

(1) 連續性假設。假設F(X)是連續的、關于X可微的,當武器裝備自身的性能指標變化時,效能也會連續變化。

(2) 邊際效益遞減規律。武器裝備效能增大到某數值后,在增加相同ΔX的情況下,ΔE將會變小，所以F(X)的函數形式應為凸函數。

(3) 量綱一致性。效能指數是無量綱的,而武器裝備的性能由多種指標組成,不同的性能具有不同的量綱,需要有對性指標進行無量綱化處理。

滿足上述3個要求的函數F(X)可以表示為

(5)

式中,wi為冪指數;C為調整系數,在比較多個對象之間的指數值或統計由不同對象組成的集合的指數值時可進行數量級的調整,一般設為1。

運用冪指數法時,會涉及到多種類型的指標,這些指標的量綱也不同,需要通過對各個類型的指標進行無量綱化處理使其具有可比性。效能指標中的定量指標分為正向指標(如攔截概率)和負向指標(如保障延誤時間),可分別進行指標無量綱化處理。

對于正向指標的處理方法:

(6)

式中，MAXxi表示性能指標xi的最大值；MINxi表示性能指標xi的最小值；yi表示對xi無量鋼化后得到的性能指標。

對于負向指標的處理方法:

(7)

3.2 裝備體系保障效能評估

根據圖1裝備體系保障能力分析模型,按照裝備體系效能評估指標體系構建方法[25],將頂層能力(體系保障能力)映射為保障效能,把頂層能力以下的各層能力映射為相應的效能,保持隸屬關系不變,完成由體系能力分析模型到效能評估指標體系的映射轉換,建立如圖2所示的裝備體系保障效能指標體系,并在后續分析中通過分析裝備體系保障的流程和活動,將能力分析得出的指標對應到具體的裝備和相應活動中,形成指標矩陣以用于裝備體系保障效能評估。

圖2 裝備體系保障效能指標體系Fig.2 Support effectiveness index system of equipment system of systems

裝備體系保障效能評估步驟如下。

步驟 1單裝備單一保障效能評估。通過Sobol全局敏感性分析方法,根據式(2)計算出單裝備底層指標矩陣中能力指標Xi針對裝備體系可用度的敏感度Sxi,以此作為冪指數法中的權重,進而計算出單裝備單一保障效能。

步驟 2多裝備單一保障效能評估。通過AHP計算出裝備體系中各裝備的權重,并利用冪指數法計算出上一層級的裝備體系單一保障效能。

步驟 3裝備體系保障效能評估。在計算出多裝備單一保障效能E1，E2和E3后,用AHP確定三者權重,并用冪指數法計算整個裝備體系保障效能。

4 案例分析

本文以某裝備體系為例進行案例分析。裝備體系中的裝備類型包括:攔截武器系統LJ1、LJ2、LJ3,預警系統YJ1、YJ2、YJ3、YJ4,以及指控系統ZK1、ZK2、ZK3。由于存在不同類型裝備備件共用、保障組織重合等問題，裝備體系呈現出一體化聯合保障的特點,使得裝備體系保障效能評估不同于單一裝備保障效能評估。目前,整個裝備體系保障實行使用陣地、本級維修中心和基地級維修中心三級維修體制:使用陣地主要負責裝備現場維修與故障件更換;本級維修中心主要負責多類型裝備的備件補給和故障件維修;基地級維修中心負責向本級維修中心補充備件以及維修故障件。根據圖1裝備體系保障能力分析模型,從維修、資源補給和指揮調度3個方面對裝備體系保障效能進行評估,以便對體系保障進行優化。

4.1 裝備體系保障效能指標

根據部署方案,裝備體系需要進行保障的裝備各有若干套,每套裝備都經歷三級維修保障的流程。根據圖2裝備體系保障效能指標體系,將裝備體系保障效能指標對應到相關的裝備,形成相應的指標矩陣E1.1,E1.2,E2,E3,如表1～表4所示。指標矩陣中各指標在其變化區間內取值并對裝備體可用度進行Sobol敏感性分析,便可確定指標權重以用于裝備體系保障效能評估。

表1 裝備搶修效能(E1.1)

表2 裝備后送修復效能(E1.2)

表3 資源補給效能(E2)

表4 指揮調度效能(E3)

4.2 裝備體系保障效能仿真

裝備體系交通評估一般都采用仿真的形式進行[28-29]。本文基于多智能體對裝備體系保障效能進行仿真,并對裝備體系可用度進行敏感性分析。裝備體系保障過程中各裝備都是獨立可運作的系統,且各系統之間交互復雜,因此多智能體仿真比較適用于裝備體系保障研究[15,30]。

通過分析該裝備體系保障的流程和活動,三級維修保障主要分為兩個方面的內容:故障件維修和故障件更換。當裝備發生故障時,由使用陣地對故障件進行拆卸和更換,如果備件不足,則通過指揮調試進行逐級備件請領;同時將故障件送修至本級維修中心,如果本級維修中心不可修,則送往基地級維修中心,相應流程如圖3和圖4所示。在基于多智能體進行裝備體系保障效能仿真過程中,還需要對各型裝備的狀態變化進行建模，包括正常工作和故障兩個狀態,相應狀態圖如圖5所示。

圖4 故障件更換流程模型Fig.4 Model of faulty part replacement process

圖5 外場可更換單元及裝備狀態模型Fig.5 Model of line replaceable unit and equipment state

根據圖4和圖5,建立裝備體系多智能體系仿真模型,并依據表1～表4各指標矩陣中的指標對裝備體系保障進行仿真。

4.3 裝備體系保障效能評估

根據前文裝備體系保障效能評估的步驟,依次進行單裝備單一保障效能、多裝備單一保障效能再到裝備體系保障效能評估,便可實現對該裝備體系的保障效能評估。

首先,對單裝備指標進行Sobol敏感性分析,以表1～表4中各參數作為輸入,以體系可用度作為輸出,通過仿真計算各個指標的重要度。

以表1中LJ1的使用陣地故障隔離率X1、故障LRU拆卸時間X2和安裝時間X3為例進行敏感性分析。對Xi在其取值范圍內均勻取n個點,在取每個Xi點時令Xi隨機進行m次抽樣,獲得m個Y值(即As的值),然后根據這m個Y的均值確定VXi(EX-i(Y|Xi)),進而得出X1,X2和X3主效應值,結果如圖6～圖8所示。

圖6 計算SX1的統計數據Fig.6 Statistical data for calculating SX1

圖7 計算SX2的統計數據Fig.7 Statistical data for calculating SX2

圖8 計算SX3的統計數據Fig.8 Statistical data for calculating SX3

對于X1,抽樣n×m=11×80=880次。

對于X2,抽樣n×m=11×80=880次。

對于X3,抽樣n×m=11×80=880次。

同理得出所有指標主效應匯總，如表5所示。

表5 SX1，SX2和SX3主效應值

其次,將裝備搶修效能通過式(6)和式(7)對數據進行無量綱化處理,結果如表6所示。將表5中主效應值作為權重,代入冪指數法式(5)中,得出各類裝備所對應的效能,如表7所示。

表6 無量綱處理表

表7 E1.1裝備搶修效能計算結果

然后,通過AHP確定LJ1、LJ2、LJ3、YJ1、YJ2、YJ3、YJ4、ZK1、ZK2和ZK3這10型裝備的權重,給出兩兩比較的矩陣:

計算得出最大特征根為10.96,歸一化特征向量為

ω=[0.065,0.053,0.045,0.0151,0.116,0.111,

0.042,0.162,0.139,0.051]

一致性檢驗指標CR=0.072<0.1,檢驗通過。將特征向量作為權重,通過冪指數法計算得出E1.1裝備搶修效能為0.614,同理E1.2裝備后送修復效能為0.598。根據專家評判方法得到E1.1裝備搶修效能與E1.2裝備后送修復效能的權重分別為0.6和0.4。再根據冪指數法求得E1裝備維修效能為0.608。

最后,按照相同的步驟和算法,計算出E2資源補給效能和E3指揮調度能分別為0.586和0.613。給出E1、E2以及E3兩兩比較的矩陣:

計算得出最大特征根為3.05,歸一化特征向量為ω=[0.32,0.22,0.46],一致性檢驗通過。

將特征向量作為權重,通過冪指數法計算得出裝備體系保障效能為0.6。

5 結 論

裝備體系保障效能對裝備體系作戰任務完成有重要影響,而裝備體系一體化聯合保障的特點,使得裝備體系保障效能評估變得困難。本文首先通過能力分析得出裝備體系保障能力框架,然后在Sobol敏感性分析方法基礎上,針對裝備體系可用度進行敏感性分析,綜合冪指數法提出了裝備體系保障效能評估方法,最后運用多智能體仿真技術,針對具體裝備體系案例,將裝備體系保障效能指標體系中的各個指標作為仿真輸入,實現對裝備體系保障效能的仿真計算,得出該裝備體系的保障效能。本文提出的基于Sobol敏感性分析的裝備體系保障效能評估方法為保障效能指標體系中各指標權重的客觀計算提供了方法手段,同時該方法也可為裝備體系的效能評估問題提供借鑒。