EEMD 與HMM 在齒輪故障診斷方法中的研究

謝蓉仙 ，任 芳 ，楊兆建

（1.太原理工大學機械工程學院，山西 太原 030024；2.煤礦綜采裝備山西省重點實驗室，山西 太原 030024）

1 引言

旋轉機械在能源、動力、航天、農業、醫療等各種行業廣泛應用，而齒輪箱和齒輪是旋轉機械中不可替代的關鍵部分，尤其是齒輪，在長時間高轉速運轉條件下，其運行狀況可能會直接影響整個旋轉機械設備的正常運轉，具有舉足輕重的作用，所以對齒輪和齒輪箱進行相應的監測和故障識別診斷，保證設備安全正常運行具有非常重要的實際意義和很大的工程應用價值。

要對齒輪及齒輪箱進行故障識別和診斷，最關鍵的部分在于如何提取包含其故障的主要特征[1]。而振動信號是最容易反映齒輪故障的信息，通過分析采集儀采集到的齒輪振動信號來判斷齒輪的運行狀態和故障是比較常用的方法，大多數的齒輪故障診斷方法一般都是分析采集到的振動信號的時域或頻域等相關的特征，來判斷齒輪的運行狀態和故障類型[2-4]。文獻[5]是將EEMD能量熵與支持向量機結合，對齒輪進行故障診斷，文獻[6]是利用EEMD 的多尺度模糊熵對齒輪進行故障識別和診斷，提高了診斷精度，文獻[7]是利用EEMD 自適應形態學解調方法對齒輪進行故障診斷，文獻[8]研究了振動信號的特征提取方法，用隱馬爾科夫模型（HMM）來識別和判斷風電機組齒輪箱故障，文獻[9]采用隱馬爾科夫模型（HMM）和改進距離測度法對齒輪箱進行故障識別診斷，取得比較好的效果。

總體平均經驗模態分解（EEMD）方法非常適合用于處理非線性、非平穩的齒輪振動信號，而且與EMD 相比，抗模態混疊能力更強，而且對于不同的齒輪故障信號，經EEMD 處理后，在時間尺度上會有不同的復雜度，而且在某些特定的頻段會有很明顯的區分度。隱馬爾科夫模型（HMM）在模式分類方面有很強的優勢，特別適合用來處理非線性、非平穩的各類振動信號[10]。目前，關于EEMD 和HMM 這兩種故障診斷方法，還處于單獨應用的階段，將兩種方法組合應用的研究還是非常少的。然而，在單獨使用EEMD 方法時，經常需要依靠有經驗的技術人員通過圖形或者數據等信息來判斷齒輪的工作狀態和運行狀況，在各種主觀因素的影響下，會使故障診斷精度和準確率大大降低。而HMM 在很大程度上并不依賴于專家的經驗，操作方便簡單，在信號分析和模式識別領域應用非常廣泛，但是在旋轉機械故障診斷這方面的研究與應用還是非常少的。因此，提出EEMD 與HMM 的齒輪故障診斷方法。利用EEMD 方法將采集到的齒輪原始振動信號進行分解，以能量為元素，計算并提取不同尺度的能量比，構造特征向量，作為齒輪不同故障的狀態特征參數，最后用HMM 故障診斷模型進行分類和識別，進而判斷齒輪的工作狀態及故障類型。

2 EEMD 與HMM 齒輪故障診斷

2.1 EEMD

EEMD 是對EMD 的改進，其核心思想是將高斯白噪聲頻譜均值為零的原理以及頻率均勻分布的特性加入到算法中[11]，從而減小了高斯白噪聲作為時域分布參考結構所造成的影響。當在采集到的原始振動信號中加入滿足條件的高斯白噪聲后，可以改變信號極值點的分布，這樣就會令信號在不同的尺度上具有連續性，在很大程度上減少了模態混疊現象。

EEMD 算法步驟簡述如下：

（1）在采集到的齒輪原始振動信號y（t）中添加均值為零，標準差為常數的高斯白噪聲信號ni（t），即：

式中：yi（t）—第i 次添加高斯白噪聲后的總體信號；

（2）對得到的總體信號yi（t）做EMD 分解處理，就可以獲得各階IMF 分量cij（t）和一個殘余分量ri（t），式中cij（t）為第i 次添加白噪聲并分解后所獲得的第j 個IMF 分量；

（3）循環以上步驟（1）～（2）N 次，每一次所添加的高斯白噪聲都是隨機的，并不相同；

（4）將分解后獲得的各階IMF 分量做總體平均運算處理，目的是減小每次添加的高斯白噪聲對真實的IMF 造成的影響，得到最終的結果。

EEMD 方法從齒輪原始振動信號中逐步分離出各階IMF 分量（由高頻到低頻），得到原始振動信號在不同時間尺度上的窄帶分量，完成振動信號的自適應多尺度化處理。高斯白噪聲的幅值以及EEMD 分解次數是EEMD 分解過程中最重要的兩個參數，一般情況下所添加高斯白噪聲的標準差是原始信號標準差的（0.1～0.4）倍，在分解過程中，選取添加的高斯白噪聲的幅值為原始振動信號標準差的0.1 倍，EEMD 分解的次數為50 次。

2.2 HMM

隱馬爾科夫模型（HMM）是關于時間序列的一種統計模型。因為旋轉機械的振動信號與語音信號非常相似，所以把HMM 方法引入到旋轉機械故障診斷中來。隱馬爾科夫模型是馬爾可夫鏈的一種，系統的狀態序列不可以直接觀測到，但可以通過觀測序列來推斷，每一個觀測序列都是由一個具有相應概率密度分布的狀態序列產生的，許多不同的狀態序列可能會以不同的概率產生相同的觀測序列。HMM 主要包括五個元素，2 個狀態集合和3 個概率矩陣：

（1）馬爾科夫鏈的狀態數目N，記N 個狀態分別為x1，x2，…xN，t 時刻馬爾可夫鏈所處的狀態為 qt，則 qt∈（x1，x2，…xN）。

（2）每個狀態的觀測值數目M，記M 個觀測值分別為y1，y2，…yM，t 時刻的觀測值為 Qt，則 Qt∈（y1，y2，…yM）。

（3）初始概率分布矩陣π，記N 個概率分布分別為π1，π2，…πN，則 π∈（π1，π2，…πN）。

（4）狀態轉移矩陣A，A=（aij）N×N，其中狀態轉移概率為：

（5）觀測概率矩陣 B，B=（bjk）N×M，其中觀測概率為：

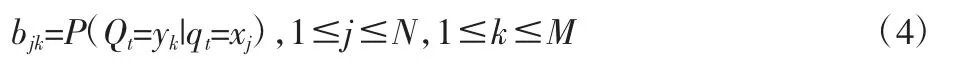
HNM 的模型為 λ=（N，M，π，A，B），簡化為 λ=（π，A，B）。只要給定相應的λ，模型就可用于產生多個任意長度的觀測序列，在這里，給定觀測序列組成的訓練集，就可以估計模型的參數，實際上，HMM 是對標準馬爾科夫模型的擴展和改進，增加了觀測序列和這些狀態與隱含狀態之間的概率關系。HMM 采用前向一后向算法來計算模型的輸出概率，即在給定模型λ 的條件下產生觀察序列O 的概率P（O|λ）；采用Viterbi 算法用于尋找測試時間序列最優狀態序列，即解決在給定觀測序列O 和HMM 模型λ=（A，B，π）時，確定該觀測序列對應的最接近真實狀態的狀態序列；采用Baum-Welch 算法完成模型參數估計，即在給出觀測序列O 和HMM 模型λ=（A，B，π）時，通過調整模型相關的參數，最后獲得一個最佳的優化模型，使概率P（O|λ）達到最大。

2.3 EEMD 和HMM 齒輪故障診斷流程

在對齒輪進行故障識別和診斷的過程中，最核心的部分就是如何對故障特征進行分析。當齒輪出現故障時，其振動信號由于調幅調頻現象會出現強烈的非平穩特性，在不同的故障中表現出來的頻率分布是不一樣的，這樣齒輪振動信號的能量分布也會不一樣，就可以利用能量熵以及各頻帶的信號能量占總能量的百分比作為特征向量，來反映齒輪的工作運行狀態。齒輪故障診斷流程圖，如圖1 所示。

圖1 齒輪故障診斷流程Fig.1 Gear Fault Diagnosis Process

采用EEMD 和HMM 的齒輪故障診斷方法步驟為：

（1）分別采集正常、磨損、缺齒和斷齒四種不同狀態下的齒輪箱振動信號；

（2）對四種不同的齒輪狀態分別采集60 組振動信號，然后均進行EEMD 分解處理，最終得到一系列的IMF 以及對應的能量熵（分解得到的IMF 數為8）；

（3）每種狀態選取包含主要故障信息的60 組數據；

（4）以能量為元素，求出不同狀態每組數據的能量比，然后構造特征向量T；

（5）將齒輪不同的工作狀態對應的30 組特征向量T 做HMM模型庫訓練，將已經訓練好的HMM 模型庫作為一個新的分類器來進行測試、識別和診斷；

（6）將每種狀態其余30 組特征向量T 分別輸入到訓練好的HMM 診斷模型庫中，計算每一次輸入的lgP（O|λ），輸出診斷結果的數據，找出最大的對數似然函數值，所對應的狀態很大程度上就是齒輪目前的工作狀態。

3 故障診斷實例

3.1 實驗設備

齒輪故障模擬實驗臺，如圖2 所示。實驗臺上裝有振動傳感器，實驗采用DHRMT 系統，可模擬旋轉機械多種工作狀態及振動，可以進行齒輪、軸、滾動軸承等多種零件不同狀態的分析及診斷。實驗系統包括齒輪箱、滾動軸承及軸系，由變速驅動電機、軸承、齒輪箱、軸、偏重轉盤、底座、調速器等組成。滾動軸承可模擬的故障有：軸承內圈損傷、外圈損傷、滾珠損傷；軸可模擬的故障有：不平衡（或葉輪不平衡）和不對中；通過更換有缺陷的齒輪，可模擬齒輪磨損、缺齒和斷齒故障，在這里只進行齒輪的故障模擬，實驗中磨損狀態的齒輪是將正常齒輪每個齒面切薄0.3mm，斷齒狀態齒輪是切掉正常齒其中一個齒的一部分，缺齒狀態齒輪是切掉正常齒輪的一個完整齒。實驗齒輪箱設置，如圖3 所示。齒輪箱為一級傳動，齒輪箱內部有兩個齒輪，分布在兩根軸上，齒輪1 為主動輪，固定在軸1 上，齒數為44，齒輪2 固定在軸2 上，齒數為60，故障齒輪為齒輪2。

圖2 齒輪故障模擬實驗臺Fig.2 Gear Failure Simulation Test Bench

3.2 實驗方案

齒輪箱設置示意圖，如圖3 所示。在實驗中，設置了三種故障，磨損、缺齒和斷齒，齒輪的磨損故障在外觀上與正常齒輪相比并不明顯。實驗系統采用DH2010 采集儀及相應的數據采集軟件，設置的采樣頻率為5kHz，并且持續采樣20s，同時齒輪每種工作狀態各采集60 組振動信號。

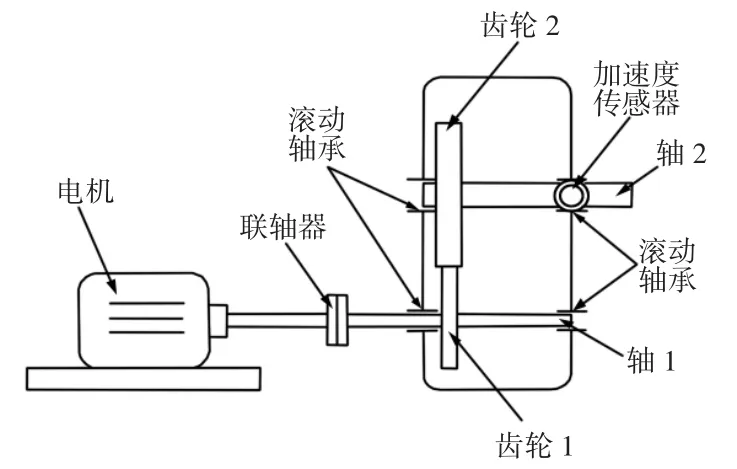
圖3 齒輪箱設置示意圖Fig.3 Gear Box Setting Diagram

以能量為元素，計算所有240 組數據經過EEMD 分解后產生的各階IMF 分量（在這里取前8 個）的能量熵以及能量比，斷齒齒輪的EEMD 分解結果，如圖4 所示。用能量比構造特征向量，限于篇幅，齒輪每種狀態只選擇4 組數據，如表1 所示。選取齒輪每種工作狀態對應的的前30 組特征向量作為HMM 的訓練數據，每種工作狀態對應的后30 組特征向量進行測試，對齒輪的工作狀態進行分類、識別和診斷。

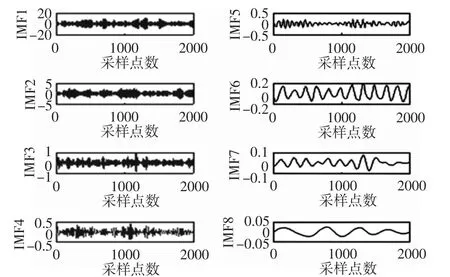
圖4 斷齒齒輪振動信號EEMD 分解結果Fig.4 EEMD Decomposition Result of Broken Tooth Gear Vibration Signal

表1 齒輪不同工作狀態下的特征向量Tab.1 Characteristic Vector of Gears under Different Working Conditions

3.3 實驗結果與分析

數據輸入HMM 模型診斷庫后的輸出結果為對數值，其值越接近于零，代表和真實的齒輪工作狀態相似度越高。在HMM 的訓練過程中，隨著迭代次數的逐漸增加，輸出的最大似然估計值的對數最終會達到收斂誤差，HMM 的訓練曲線，如圖5 所示。

圖5 HMM 的訓練曲線Fig.5 HMM Training Curve

針對齒輪的四種不同的工作狀態，每種狀態用30 組特征向量進行診斷測試，4 種HMM 模型診斷庫的測試結果，如表2～表5所示。診斷統計結果，如表6 所示。由此可以計算出EEMD-HMM齒輪故障診斷方法平均識別率為95.8%。

表2 正常齒輪測試數據4 種HMM 模型的輸出對數似然概率Tab.2 Output Log Likelihood Probability of Four HMM Models for Normal Gear Test Data

表3 磨損齒輪測試數據4 種HMM 模型的輸出對數似然概率Tab.3 Output Log Likelihood Probability of Four HMM Models for Wear Gear Test Data

表4 缺齒齒輪測試數據4 種HMM 模型的輸出對數似然概率Tab.4 Output Log Likelihood Probability of Four HMM Models for Missing Gear Test Data

表5 斷齒齒輪測試數據4 種HMM 模型的輸出對數似然概率Tab.5 Output Log Likelihood Probability of Four HMM Models for Broken Tooth Gear Test Data

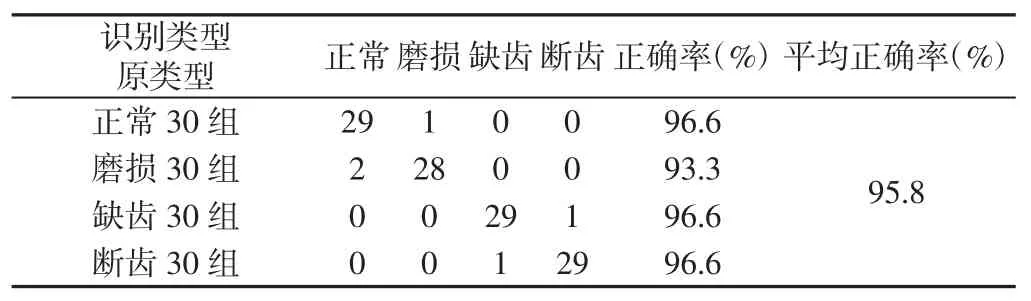
表6 診斷結果統計Tab.6 Diagnostic Result Statistics

4 總結

提出一種將總體平均經驗模態分解（EEMD）和隱馬爾科夫模型（HMM）結合的齒輪故障診斷方法，首先利用EEMD 方法對采集到的齒輪原始振動信號進行分解，得到各階IMF 分量，再以能量為元素求能量比構造特征向量，將得到的故障特征向量作為輸入參數輸入HMM 模型診斷庫進行故障識別和診斷。經研究分析得出如下結論：（1）EEMD 在處理非線性、非平穩信號時大大減少了模態混疊現象，可以有效提取故障特征信息；（2）HMM 與其他智能診斷算法相比，算法相對簡單，訓練時間短，速度快，故障識別準確率高。試驗結果表明，將該方法用于齒輪的故障識別和診斷，準確率達到了96%左右，具有較強的適應能力，可以有效的識別齒輪常見的磨損、缺齒和斷齒故障。