雙螺桿真空泵新型變速螺線型轉子的研究

魏蜀紅，趙 峰，夏明川，王 君

（1.中國石油大學（華東）化學工程學院，山東 青島 266580；2.中國石化青島煉油化工有限責任公司，山東 青島 266580）

1 引言

雙螺桿真空泵因其抽氣腔干式無油、運行平穩可靠和適應性強等優點，廣泛應用于石油化工、食品制藥、真空熱處理、納米制造和國防技術等領域[1]。雙螺桿真空泵的主要部件是相互嚙合的兩個螺桿轉子，螺桿轉子及其轉子截面型線的設計是其核心技術。目前傳統的截面型線為擺線-漸開線型，采用圓漸開線和擺線連接齒頂和齒根圓弧[2]。然而，該型線存在尖點不能完全嚙合，螺桿轉子空間接觸線存在斷點，有明顯的泄漏通道。為了改善該問題，文獻[3-5]采用圓弧與擺線的等距曲線修正圓弧和圓漸開線連接處，并且在爪尖處也采用圓弧光滑連接，實現了轉子的全嚙合，但型線組成復雜。文獻[6]為了消除泄漏通道提高密封性，采用多段圓弧及其包絡線連接齒頂與齒根圓弧，增加曲線設計難度。文獻[7]繪制了變螺距螺桿轉子的嚙合線和空間接觸線。文獻[8]研究了螺桿轉子的熱力變形和最大間隙變化情況。

針對以上問題，為了實現截面型線的光滑連接和簡化設計，提出了一種變速螺線的構建理論，可用一條曲線光滑連接齒頂和齒根圓弧，推導了截面型線方程，對比了現有轉子和所提出的新型螺桿轉子的空間接觸線和應力分布，對提高雙螺桿真空泵的工作性能具有重要的意義。

2 型線理論

2.1 曲線嚙合原理

螺桿轉子截面型線的共軛曲線指的是在同步異向回轉運動的任意時刻，另一轉子截面型線上與已知截面型線完全嚙合的曲線，假定第一截面型線上某一組成曲線的矩陣方程為r1（t），該曲線在運動時形成的曲線族可以通過坐標變換得到，曲線族的公式為：

式中：M12—動坐標系xO1y 到動坐標系xO2y 的變換矩陣：

式中：φ—截面型線的旋轉角；求解t 與φ 的關系：

將式（3）帶入坐標變換公式（1），即得到共軛曲線的方程。

2.2 變速螺線的構建理論

阿基米德螺線亦稱為等速螺線，即一點P 沿動射線O1P 以等速率運動的同時，該射線又以等角速度繞點O1旋轉，在圖1 中表示為 v（t）=c1，ω（t）=c2。但由此不能光滑連接齒頂圓弧與齒根圓弧，通過改變點P 的運動方式，可以實現螺線在曲線交點處的光滑連接。

圖1 變速螺線生成原理Fig.1 Generation Principle of Variable Speed Spiral

點P 的初始位置在半徑為R3的齒根圓弧點A 處，終止位置在半徑為R1的齒頂圓弧點C 處，如圖1 所示。點P 沿射線O1P 做徑向速度v（t）運動的同時，射線又以角速度ω（t）繞點O1旋轉。且vA（t）=vC（t）=0，也就是在A 點和C 點處極徑O1P 的增長速率為0，曲線曲率分別為R3和R1。

根據點P 在射線O1P 方向先加速后減速的運動規律，設徑向速度v（t）為正弦函數：

則點 P 徑向位移為：R（t）= ∫v（t）dt，將 R（0）=R3，R（θ）=R1帶入上式，得到點P 位移方程為：

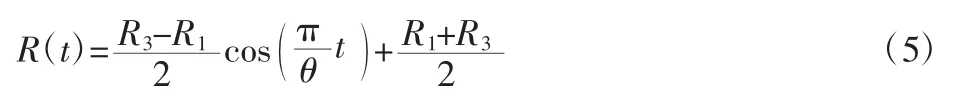
式中：θ—角度參數。

角速度ω（t）決定了點P 轉過角度的快慢，點P 的旋轉角函數為 φ（t）= ∫ω（t）dt。則得到變速螺線的方程：

圖2 不同旋轉角函數對應的變速螺線Fig.2 Variable Speed Spirals Corresponding to Different Rotational Functions

φ（t）可選取不同的函數，取 φ（t）分別為一次、二次、三次多項式時，且均通過點A 和點B，生成的三種變速螺線，如圖2 所示。分別對應螺線 ABC1，ABC2，ABC3。由圖中看出 φ（t）可以影響螺線圓心角和掃過的面積，可以對提高螺桿轉子截面面積利用率提供一種途徑。

3 新型截面型線

3.1 傳統截面型線

傳統截面型線，如圖3 所示。由圓漸開線AB、齒頂圓弧BC、擺線CD 和齒根圓弧DA 組成。其在點A、點B 和點C 處存在尖點，容易引起應力集中；在A 點附近嚙合不完全，存在如陰影所示的泄漏通道，造成壓力損失和流量減小。

圖3 傳統截面型線Fig.3 Traditional Cross-Section Profile

3.2 變速螺線型截面型線

根據嚙合原理和所構建的變速螺線，提出了一種變速螺線型轉子截面型線，采用變速螺線替代圓漸開線，圓弧和擺線等距曲線代替擺線。為了使左右轉子截面型線完全相同，AB 段采用變速螺線，BC 段采用變速螺線包絡線。截面型線由6 條曲線組成：變速螺線 AB，變速螺線包絡線 BC，三段圓弧（CD、DE、FA）和擺線EF，如圖4 所示。

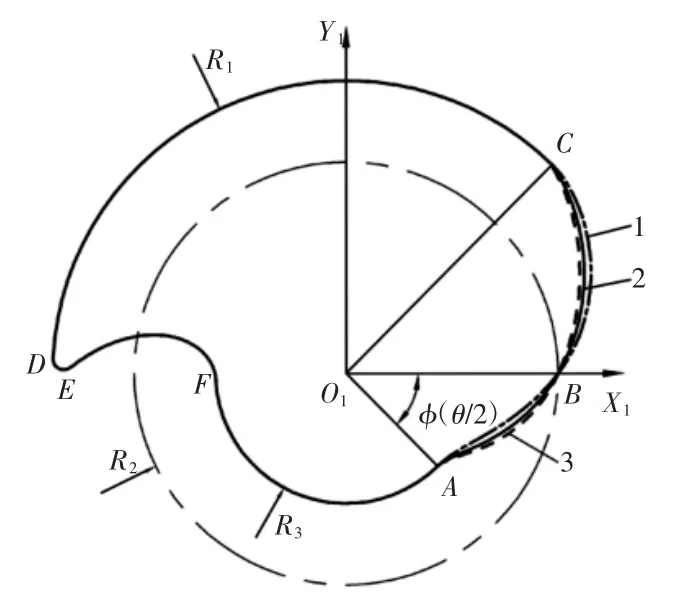
圖4 新型截面型線Fig.4 New Cross-Section Profile

3.2.1 變速螺線及其包絡線方程

變速螺線在構成截面型線時需順時針旋轉一個角度，使得點B 位于節圓和與橫軸交點處，旋轉角度的求解：

變速螺線AB 的方程可由式（6）順時針旋轉φ（θ/2）得到：

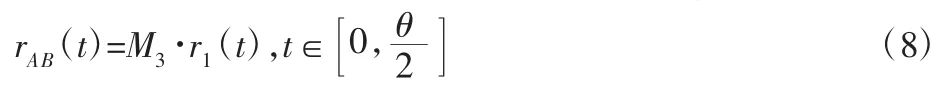
式中：M3—旋轉矩陣：

變速螺線包絡線BC 方程由式（1）～式（3）求得：

3.2.2 旋轉角函數的影響

點劃線1、實線2 和虛線3 表示旋轉角函數φ（t）為一次多項式t、二次多項式t+t2、三次多項式t+t2+t3對應的變速螺線AB 和變速螺線包絡線BC，如圖4 所示。三種螺線構成的型線面積明顯不同，其各自的面積利用率，如表1 所示。隨著旋轉角函數φ（t）次冪的增加，變速螺線及其包絡線組成的截面型線面積利用率逐漸增加。

表1 不同旋轉角函數對應的面積利用率Tab.1 Area Utilization Ratios Corresponding to Different Functions

4 性能對比

在以下對比中變速螺線的旋轉角函數均為φ（t）=t+t2+t3。

4.1 嚙合特性分析

各段曲線的嚙合線求解：

式中：M01—從動坐標系xO1y 到靜坐標系XO1Y 的變換方程：

得到傳統截面嚙合線和變速螺線型截面嚙合線，如圖5（a）、圖5（b）所示。

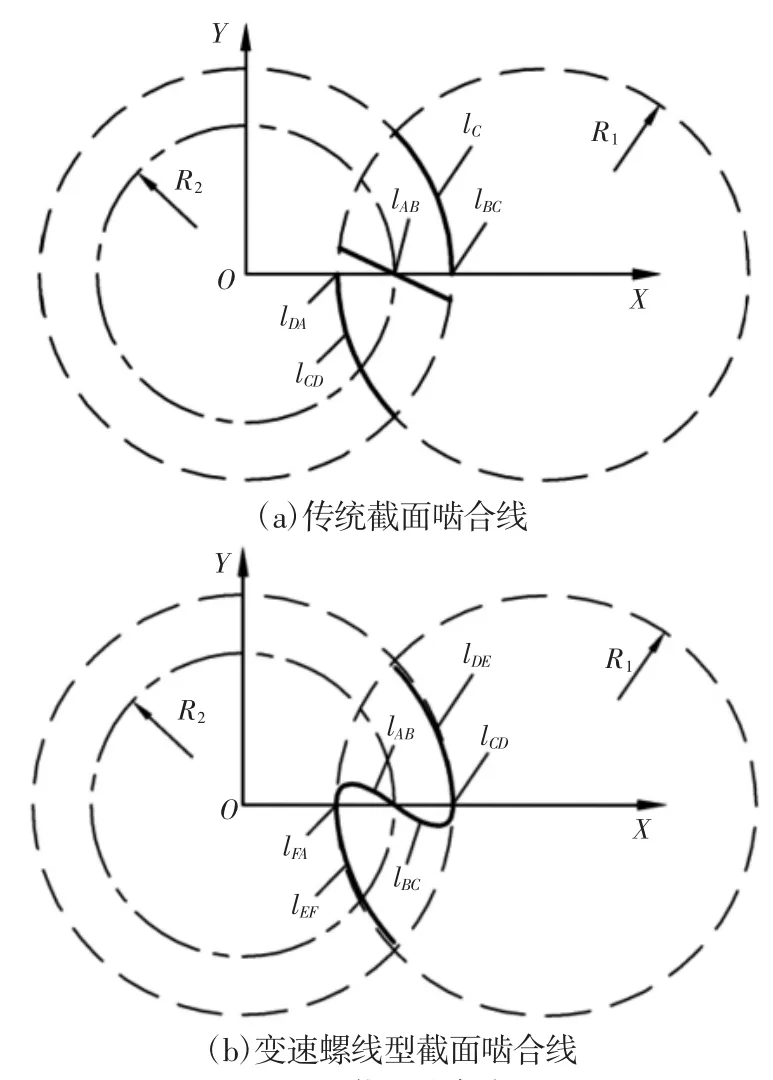
圖5 截面嚙合線Fig.5 The Meshing Lines of Cross-Section Profiles

4.2 空間接觸線

空間接觸線是雙螺桿真空泵的主要泄漏通道之一，是由螺桿轉子與轉子之間非接觸式嚙合，轉子與泵腔之間留有的間隙產生的。接觸線兩側是壓力不均的氣體介質，如果接觸線不連續，高壓側氣體通過接觸線缺口向低壓側泄漏，并且一般認為其長度越短螺桿轉子的密封性越好。使傳統截面型線轉子和變速螺線型轉子具有相同的轉子齒厚，兩種轉子的空間接觸線，如圖6 所示。

圖6 螺桿轉子空間接觸線Fig.6 Contact Linesof Screw Rotors

空間接觸線是嚙合線在螺桿轉子曲面上的投影。嚙合線不連續，如圖5（a）所示。造成空間接觸線在齒根和齒頂處有斷點，如圖6（a）所示。導致如圖3 陰影處所示的泄漏通道。而變速螺線的嚙合線和空間接觸線是光滑連續的，如圖5（b）、圖6（b）所示。左右轉子完全嚙合，不存在泄漏通道，因而具有較好的級間密封效果。

4.3 應力分布

在雙螺桿真空泵工作狀態下，對傳統螺桿轉子和變速螺線型螺桿轉子施加相同的邊界條件。入口壓力為3kPa，出口壓力為100kPa，入口溫度300K，出口溫度370K，轉速2940r/min。兩種轉子的應力分布，如圖7 所示。

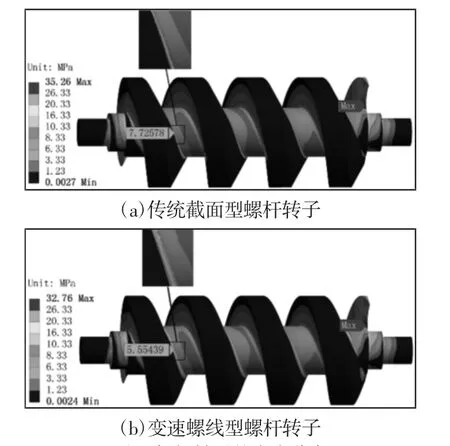
圖7 螺桿轉子的應力分布Fig.7 Stress Distributions of Screw Rotors

應力多集中于齒根處，最大應力值位于出口端齒根處。傳統截面型轉子最大應力值為35.26MPa，局部放大圖處齒根應力集中明顯，取一點值為7.73MPa，如圖7（a）所示。變速螺線型轉子最大應力值為32.76MPa，較傳統截面型轉子減小7.09%，局部放大圖處沒有應力集中，應力分布更為平緩，取相同的點應力值為5.55MPa，也小于傳統截面型轉子，如圖7（b）所示。這是因為傳統截面型轉子齒根面與斜齒面之間過渡曲率突變較大，變速螺線型轉子能夠完全光滑過渡。

5 結論

（1）提出了一種變速螺線的構建理論，求解了其方程形式，該螺線可光滑連接齒根和齒頂圓弧，此理論對爪式真空泵、羅茨風機和滑片真空泵等流體機械有一定的應用價值。

（2）提出了一種變速螺線型轉子截面型線，采用變速螺線及其包絡線替代傳統截面型線的圓漸開線，解決了截面存在尖點的問題，旋轉角函數次冪增加時，轉子截面的面積利用率有所提高。

（3）變速螺線型轉子相比于傳統截面轉子具有光滑連續的嚙合線和空間接觸線，不存在泄漏通道，因而具有較好的級間密封效果；齒根應力分布更為平緩，最大應力值減小7.09%，轉子受力情況好。