薄壁圓筒孔徑測量誤差分析

朱振偉 ，王亞龍 ，張 瑞 ，3

（1.河南機電職業學院機電工程學院，河南 新鄭 451191；2.鄭州大學機械工程學院，河南 鄭州 450001；3.洛陽鄭大物聯科技有限公司，河南 洛陽 471300）

1 引言

基于工序的智能化生產線內部（產線內）檢測是實現產線智能制造的基礎要求。其中，粗加工工序的產線內檢測往往處于被忽視的地位，但這一環節的質量控制對后續工序生產有著決定性的影響。同時，由于是粗加工，相應的基準尚未建立，這就給檢測帶來了難度。

薄壁圓筒的精密加工是一個難點，產線內的檢測是提高薄壁圓筒加工質量的有效手段。以鑄造圓筒鋼毛坯來制造薄壁圓筒的第一道加工工序—內孔粗車的線內檢測為研究對象，對薄壁圓筒粗加工檢測的實現進行研究[1-2]。

2 測量內容要求及原理

鑄造圓筒鋼毛坯經粗切形成代加工的毛坯，進入數控車進行內孔加工。本道工序加工完成后需檢測的內容有：將圓筒工件沿著主軸方向分為三個截面，分別對三個截面的直徑進行多次測量，并初步評估圓度。

由于只加工了內徑，毛坯端面尚未加工，這就造成了圓筒母線高度不一致，外表面仍是毛坯面的狀況。同時由于是產線內部的檢測，對檢測的節拍和工件的處理也提出了要求。在此條件下，采用激光傳感器結合構造的接觸式定位基準，搭建了相應的測量原理[3]。

使用兩圓柱銷定位塊限定薄壁圓筒的位置，并在圓筒外側兩圓柱定位銷中點連線的中間位置施加作用力，使得圓筒工件中心軸與測量裝置軸心線對正平行，實現三點定圓。激光傳感器軸線處于三點圓的直徑上，傳感器后置測頭頂銷與筒壁接觸，由傳感器讀數即可得到圓筒的內徑，如圖1 所示。

圖1 測量方案原理示意圖Fig.1 Schematic Diagram of Measurement Scheme Principle

由于該裝置必然存在加工和裝配誤差，現對裝置誤差的來源及其對測量結果的影響分析如下。可將兩柱定位塊等效為圓盤定位塊，便于原理說明解析。簡化測量原理空間示意圖，如圖2 所示。

圖2 測量裝置空間示意圖Fig.2 Space Schematic Diagram of Measuring Device

3 數學模型建立

實際測量時，傳感器和定位塊相對于理想測量位置會發生偏心，傾斜等誤差影響因素。針對每種因素單獨建立分析模型，并將各模型的分析結果進行疊加，得到整體誤差。

理想孔徑測量截面示意圖，如圖3 所示。

圖3 無誤差影響因素測量截面圖Fig.3 Measurement Sectional View without Error Influencing Factors

設AB 為激光傳感器測量值，AB=a；BC 為激光傳感器長，BC=b；CD 為測頭頂銷長度，CD=c，如圖3 所示。AD 為傳感器測量線，此時，AD=a+b+c。則測量誤差，如式（1）所示。

式中：d—直徑實際測量值；d0—理想圓筒直徑值。

（1）當傳感器發生平移偏心時，測量截面示意圖，如圖4 所示。設實際測量直徑距離理想直徑AD 偏心距為OO1，OO1=e，由于偏心方向對結果的影響是一樣的，因此e>0。

圖4 偏心測量截面圖Fig.4 Measurement Sectional View of Eccentricity

此時直徑實際測量線是A1D1，設其值為d1，則：

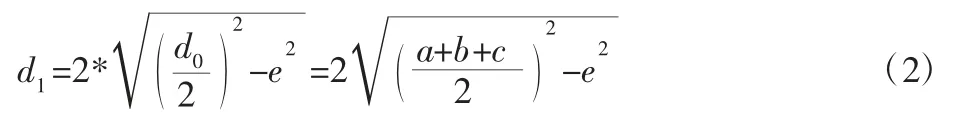
帶入式（1）：

式中：當 e 為 0 時，d1=d0，δ1=δ0。

（2）當傳感器在有偏心距的基礎上發生水平面上的傾斜時，測量截面示意圖，如圖5 所示。

圖5 水平面上傾斜測量截面圖Fig.5 Inclination Measurement Sectional View on Horizontal Plane

圖6 垂直平面上傾斜測量截面圖Fig.6 Oblique Sectional View of Vertical Plane

傳感器偏心距離e 后，傳感器測量線D2A2繞D2點旋轉角度β，由于定位塊的限制D2A2的旋轉方向是單向的，故β>0°。此時直徑實際測量線A3D2，設A3D2=d2，則：

式中：β=0 時，d2=d1，δ2=δ1。

（3）當傳感器繼續向上發生垂直方向的傾斜時，測量截面圖，如圖6 所示。

測量線D2A2在垂直面上繞A3點逆時針旋轉角度γ，得到測量線A3D3，由于A3D3順時針旋轉與逆時針旋轉角度關于A3D2對稱，旋轉方向對結果影響一樣，因此γ>0°。此時直徑測量線為A3D3，設 A3D3=d3，則：

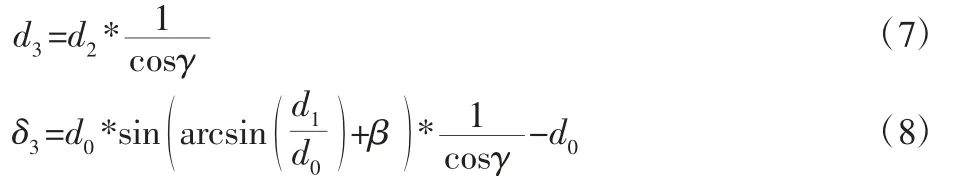
式中：γ=0 時，d3=d2，δ3=d2。

（4）在以上幾種影響因素下，測頭頂銷安裝發生偏折角度α，由于偏折方向對結果的影響是一樣的，因此α>0°。頂銷尺安裝偏折截面圖，如圖7 所示。

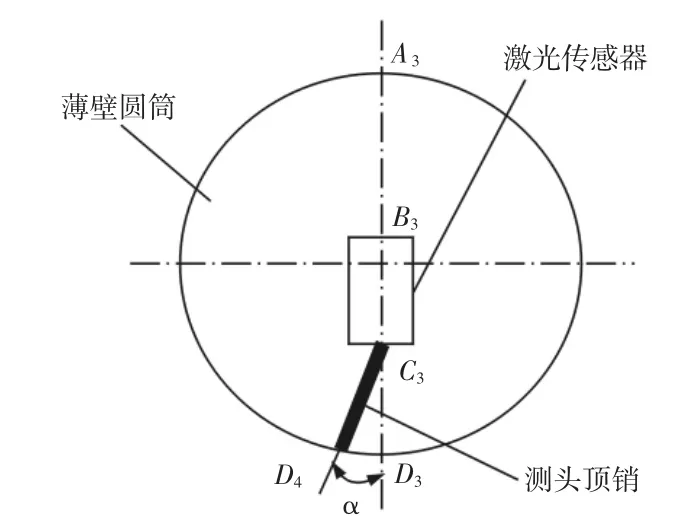
圖7 安裝偏折測量截面圖Fig.7 Measurement Sectional View of Installation Deflection

實際直徑測量線為折線A3C3D4，測量值d 變化，主要是由頂銷頂到內壁位置偏移變化引起，垂直距離縮小，而c 值為標定的固定值，但是這一段縮短的值Δc 被激光傳感器測量距離值a 補償。設此時測量直徑值為d4，則：

相對于測量直徑，就會多出補償值Δc。

帶入式（1），則：

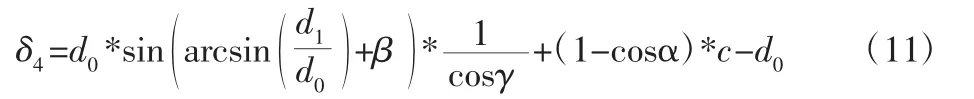
通過以上分析，建立的綜合誤差模型公式為：

4 實例模型求解驗證

4.1 影響因素變量范圍的確定

在實際工程應用中，以某薄壁圓筒缸套為實驗對象，加工誤差要求0.1mm，測量誤差要求0.05mm。根據測量裝置的結構尺寸，圓盤定位塊直徑80.80mm，高度41.8mm。偏心距e 根據定位塊的位置限制，其定義域為0≤e≤0.30mm，β、γ 兩角的范圍，根據定位塊在圓筒工件中的最傾斜位置角度確定為-0.40°≤β≤0.40°，0°≤γ≤0.40°。測頭偏折角度 α，根據安裝表面的精度，包括平行度和垂直度要求，分別取6 級精度、7 級精度和8 級精度，通過公式計算，得到分別取三個值 α1=0.43°，α2=0.55°，α3=0.65°。轉化為求解數學模型的最優解問題[4-7]。

4.2 采用MATLAB 進行求解

目標函數為式（12）。

根據測量裝置實際結構尺寸得，d0為81.1mm，c 為6.95mm。

約束條件如下：0≤e≤0.30mm；0≤β≤0.40°；0°≤γ≤0.40°；α1=0.43°；α2=0.55°；α3=0.65°。

在MATLAB 中使用Colormap 等函數可分別得到α1=0.43°，α2=0.55°，α3=0.65°下的誤差范圍立體圖像，如圖8 所示。

圖8 三個分別對應的誤差范圍立體圖Fig.8 The Error Range Stereogram of Three

如以上三圖所示，孔徑誤差三維立體分布示意圖，三個坐標軸分別代表三個變量e、β 和γ，圖上數據點的顏色代表孔徑誤差值的大小，圖右的圖例顯示對應顏色的數值大小。根據圖示可得孔徑誤差有正有負，變化趨勢呈扇形輻射，逐層增減。需要提取精確解，對孔徑誤差范圍進行定量分析[8]。

在 MATLAB 中的使用 max 和 min 函數，分別得到 α1、α2、α3對應直徑誤差最大值δmax最小值δmin，如表1 所示。

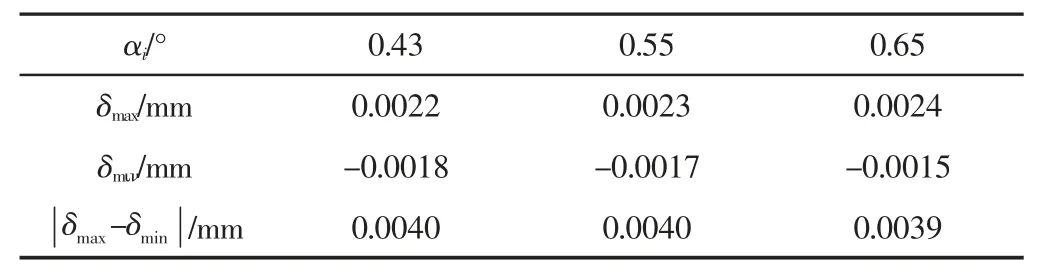
表1 不同值對應的孔徑誤差Tab.1 Aperture Error Corresponding to Different Alpha Values

如表1 所示，孔徑誤差范圍保持在0.0040mm 內，遠遠小于工程要求的精度范圍0.05mm，所以上述建立的模型符合工程要求。

5 實驗數據驗證

通過以上模型的建立和求解分析，可得使用圓盤定位塊限定傳感器的軸心與工件圓筒的軸心的相對位置，保證圓心定位精度從而測量圓筒工件的直徑的方案在理論上是可行的，但是需要進行實驗，并通過分析實驗數據進行驗證[9-10]。根據方案原理，建立工作實驗臺。實驗中確定零部件表面精度都為8 級，實驗裝置，如圖9 所示。

圖9 孔徑測量實驗裝置圖Fig.9 Experimental Setup for Aperture Measurement

使用如圖9 所示的裝置，在對測頭頂銷標定后，將直徑為81.1mm 的圓筒工件任意放置在工作臺上，通過氣缸傳動引導定位塊對圓筒工件進行定位和對準測量基準線，外加作用力使得定位塊與圓筒工件內壁緊貼。由單激光傳感器讀數即可得到測量的內徑值，在圓筒工件中選取某三個截面作為測量面，利用本實驗裝置對該測量面進行掃描測量，并重復實測，共測量50 組數據，統計孔徑測量數據，將數據繪制折線圖，如圖10 所示。

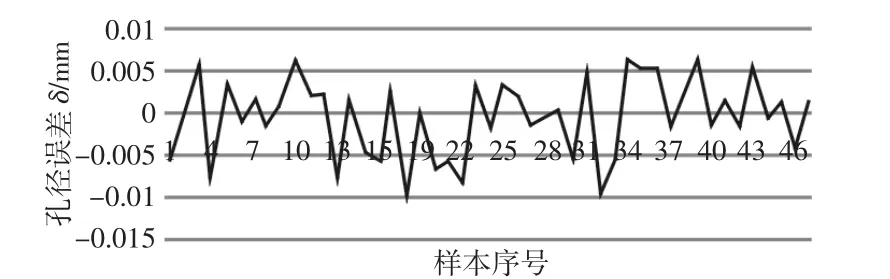
圖10 實測孔徑誤差折線圖Fig.10 The Line Chart of Measured Aperture’s Error

數據結果顯示誤差穩定在-0.01≤δ≤0.006mm 范圍內，誤差范圍控制在0.004mm 內。這與在MATLAB 中通過對數學模型求解計算的結果對比，誤差值具有一定的偏差，但是誤差范圍相等。通過分析，在實際的測量過程中，整個測量系統引入的格外的誤差，而在模型求解過程中對一些因素采用理想化處理，近似代替等等方式，從而使實測誤差值偏大，但是誤差穩定在工程要求范圍內。而實測的誤差值也符合工程要求。

6 結論

在利用單激光傳感器掃描測量圓筒工件內徑過程中，通過定位塊將測量裝置測量基準與圓筒工件中心軸線對齊，則影響內徑測量誤差的主要因素就由單激光傳感器在圓筒工件中的位姿決定，單激光傳感器的位姿越接近理想位姿，孔徑測量精度就越高。通過研究影響薄壁圓筒直徑測量誤差的各種單因素的綜合關系，建立數學模型，使用MATLAB 計算以及實驗數據驗證分析，得到以下結論：

（1）通過類似圓盤形定位塊圓盤定位塊限定傳感器的軸心與工件圓筒的軸心的相對位置，保證圓心定位精度從而測量圓筒工件的直徑的方案是可行的。計算精度和實測精度都達到工程需求的0.05mm。

（2）傳感器在圓筒工件內的任意位姿測量內徑時，各個變化的幾何影響因素相互疊加在一起綜合考慮對孔徑測量誤差分析是不可忽略的。

（3）上述模型建立與計算推導可為氣缸套等圓筒類零件的加工制造提供誤差控制理論的支持。

（4）對于影響圓筒類內徑測量誤差的不方便控制因素，可以轉化為測量裝置的方便計算和控制的變量，通過建模求解和實驗分析對該測量裝置的測量精度進行驗證。