基于改進Ibarra-Medina-Krawinkler 材料模型的RC 圓柱恢復力模型參數識別

代曠宇，于曉輝，王 碩，呂大剛

(1. 中國地震局工程力學研究所，中國地震局地震工程與工程振動重點實驗室，哈爾濱 150090；2. 哈爾濱工業大學土木工程學院，哈爾濱 150090)

建立具有較高精度和效率的結構有限元模型對進行合理和快速的結構抗震性能評估意義重大。在結構有限元建模過程中，不同類型的恢復力模型被廣泛用于描述材料、截面、構件和結構整體等多個尺度的非線性性能。相比于材料層次的結構建模方式[1?2]，利用構件的恢復力模型，建立結構的宏單元模型[3]可以大大簡化結構模型的復雜性，提高數值模擬的精度和效率。

要建立較為準確的構件恢復力模型，需要對已有結構構件試驗數據進行深入發掘。近年來，國內外學者基于不同類型構件的試驗數據庫，開展了一系列結構構件恢復力模型參數的識別工作。例如：Haselton 等[4]以美國太平洋地震工程研究中心(PEER)結構性能數據庫(Structural Performance Database)[5]中的255 根彎曲破壞及彎剪破壞的RC方柱的試驗數據為基礎，進行了RC 方柱恢復力模型參數的識別，并給出了恢復力模型參數的經驗預測公式。Lignos[6]搜集了超過600 根鋼結構構件及RC 構件的試驗數據并基于改進Ibarra-Medina-Krawinkler(改進I-M-K)材料模型對試驗構件的恢復力模型參數進行校準，最后給出了構件恢復力模型參數預測公式。呂大剛等[7]將可考慮捏縮的改進Bouc-Wen 材料模型結合遺傳算法對RC 梁-柱節點的恢復力模型進行了參數識別，并選用了11 個RC 梁-柱節點試驗驗證了所識別恢復力模型的準確性。此外，李長晉[8]采用Bouc-Wen 模型及微分進化算法，對銹蝕RC 柱非對稱模型參數進行了識別。Sengupta 和 Li[9]基于修正的Bouc-Wen 模型，采用遺傳算法對鋼筋RC 梁柱節點滯回參數進行了識別。Lee 和Han[10]采用可以考慮捏縮效應的Pinching4 材料模型對40 根彎剪破壞及剪切破壞柱構件進行了參數識別。Dai 等[11]搜集了103根擬靜力循環加載的銹蝕RC 方柱試件，采用改進I-M-K 材料對試件進行了參數識別，給出了銹蝕RC 柱的滯回模型。

根據已有相關研究，RC 方柱的恢復力模型參數識別工作已經得到了研究人員的廣泛關注。然而，對于建筑和橋梁結構中廣泛應用的RC 圓柱的恢復力模型參數識別工作，還未得到研究人員的充分重視。RC 圓柱與RC 方柱彼此之間在設計參數和構造措施方面均存在明顯的差異，因此，已獲得的RC 方柱的恢復力模型并不適用于RC 圓柱[4]。此外，研究人員已經積累了較多關于RC 圓柱的抗震性能的相關試驗數據，這也給RC 圓柱的恢復力模型參數識別提供了堅實的數據基礎。

鑒于上述，本文選取PEER 結構性能數據庫中76 個RC 圓柱試驗數據作為研究對象，采用峰值指向型改進I-M-K 材料模型作為基本恢復力模型，利用OpenSEES 有限元平臺對每一RC 圓柱的試驗數據進行模擬，識別出其恢復力模型參數。選取15 個RC 圓柱設計參數，建立構件的恢復力模型參數經驗預測公式(值)，并對其有效性進行了驗證。

1 RC 圓柱試驗數據的來源及標準化

采用PEER 結構性能數據庫中76 個RC 圓柱試驗數據組成本文數據庫。其中，所選擇試件的加載方式均為擬靜力低周往復加載，試件的失效模式為彎曲破壞或彎剪破壞。76 個試件的主要設計參數范圍如表1 所示。

表 1 圓柱試件的主要設計參數范圍Table 1 Range of main design parameters of circular columns

值得說明的是，在PEER 所提供的試驗數據中，RC 圓柱包括八角形(Octagonal)和圓形(Circle)兩種箍筋配筋形式。本文所選擇的RC 圓柱試件均為圓形配筋。根據文獻[5]，PEER 結構性能數據庫將RC 柱試件根據其構造類型及加載邊界條件分為5 類，并對試驗數據均采用了標準化處理，統一轉化為懸臂型柱(Cantilever)的力-位移數據。由于恢復力模型不同參數具有不同的靈敏度區間，且在不同坐標系下對恢復力模型進行參數識別的結果也差異較大。針對這一問題，本文參考文獻[12]及文獻[13]的處理方法，將所研究的RC 圓柱試驗數據，在考慮P-Δ 效應后統一轉化為彎矩-轉角的形式。

2 峰值指向型的改進I-M-K 材料模型

文獻[14]提出了一種折線型恢復力模型(I-MK 模型)，該模型可以較好地描述結構構件在往復荷載作用下的剛度和強度退化特性。Lignos 和Krawinkler[3]在I-M-K 恢復力模型基礎上，在對大量鋼結構構件及RC 構件試驗數據的模擬基礎上，進一步對I-M-K 滯回模型進行了修正(改進I-M-K模型)，重新定義了I-M-K 模型的骨架曲線中幾個參數，從而減小了I-M-K 模型參數的離散性，并對其剛度和強度在循環加載過程中的退化原則進行了改進。改進的I-M-K 材料模型可分為雙線型、峰值指向型和捏攏型三種。本研究選用峰值指向型改進I-M-K 材料模型，該材料可以考慮恢復力模型在正負方向的不對性。

3 RC 圓柱的滯回模型參數識別

需要說明的是，改進I-M-K 材料需識別的23個參數中的部分參數可根據已有文獻取為定值。

表 2 OpenSEES 中峰值指向型改進I-M-K 滯回材料模型參數及物理意義Table 2 Parameters and physical meanings of Peak-oriented modified I-M-K hysteretic material model in OpenSEES

圖 1 峰值指向型改進I-M-K 滯回材料模型Fig. 1 Peak-oriented modified I-M-K hysteretic material model

對于其余需識別的參數，可其分為骨架曲線參數和滯回耗能參數兩類并分別進行參數識別。總體的識別流程可分為2 個階段共5 個步驟。階段1：基于試驗數據的滯回模型骨架曲線參數的識別，識別參數屈服彎矩My(步驟1)、屈服轉角θy(步驟1)、硬化段轉角θcap,pl(步驟2)、峰值彎矩與屈服彎矩比a (通過硬化段剛度as·K0及硬化段轉角θcap,pl計算，見步驟2)以及軟化段轉角θpc(步驟3)。階段2：基于數值模擬的滯回模型耗能參數的識別(見步驟4 和步驟5)，識別參數Λ。5 個步驟的具體流程如下：

步驟1：將滯回曲線各循環之間剛度變化最大的點作為滯回模型骨架曲線的屈服點。連接滯回曲線零點與屈服點作為滯回模型骨架曲線的彈性段；

步驟2：判定滯回曲線中的首次出現隨位移增長而彎矩下降(亦稱為循環內退化[16])的滯回環所對應的轉角，將其作為峰值點轉角。若試件滯回曲線并未顯示出循環內退化特征，則參考文獻[11]及文獻[12]將試件加載的極限位移坐標定義為試件的峰值點。隨后，以屈服點為起始點，沿其所的滯回曲線的坐標點作切線，延伸至峰值點對應轉角，連接峰值點與屈服點作為骨架曲線的硬化段；

步驟3：以峰值點為起始點，以峰值點處下降段的斜率作為骨架曲線軟化段的斜率，連接峰值點及下降線與轉角坐標軸的交點作為骨架曲線軟化段；

步驟4：基于OpenSEES 有限元平臺，建立RC 圓柱滯回性能模擬的集中塑性宏單元模型(見圖2)。其中，零長度單元位于RC 圓柱底部，其采用改進I-M-K 材料模型進行模擬，模型骨架參數采用步驟1～步驟3 所定義的骨架點來進行定義；

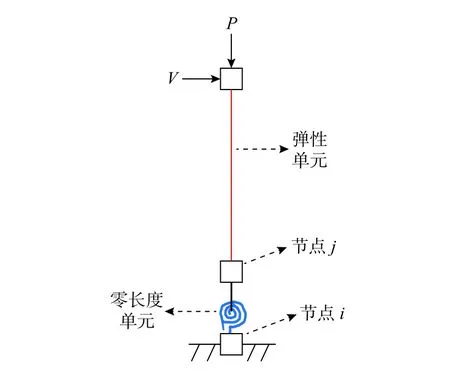
圖 2 基于OpenSEES 的RC 圓柱滯回加載分析模型Fig. 2 Numerical model of RC circular columns under cyclic loadings based on OpenSEES

步驟5：基于步驟4 所建立的RC 圓柱滯回加載分析模型，不斷調整循環退化參數值Λ，直至數值模擬結果與試驗結果相吻合，并獲得較優的循環退化參數值Λ。

對于改進I-M-K 材料模型，不同滯回耗能參數Λ 的取值會較為顯著地影響RC 圓柱的滯回規則。僅以390 號圓柱為例，圖3 給出了Λ=0.1、0.5和1.0 時，RC 圓柱的模擬滯回曲線及其與試驗曲線的對比。由圖3 可見，在相同的骨架曲線基礎上，不同的Λ 取值對應的RC 圓柱滯回曲線相較大。基于上述情況，本文采用循環迭代方式對各試件的較優Λ 值進行識別，取Λ 的初始值為0.1，步長為0.05，逐級提升Λ 值直至模擬精度滿足要求。圖4 給出了RC 圓柱恢復力模型中較優Λ 值的搜索過程。

根據上文介紹的RC 圓柱恢復力模型參數的識別過程，分別對76 根RC 圓柱滯回加載試驗進行數值模擬，獲得每一RC 圓柱所對應的改進I-M-K材料模型的骨架和滯回耗能參數，如表3 所示。為了說明基于改進I-M-K 材料模型的RC 圓柱恢復力模型參數識別過程，選取兩個典型RC 圓柱的識別結果進行說明，見圖5(a)和圖5(b)。所選取的兩個RC 圓柱試件在PEER 結構性能數據庫中的編號分別為390[17]和309[18]。

值得說明的是，大部分圓柱滯回加載試驗數據并未出現明顯軟化段。為了模擬RC 圓柱在實際地震中可能出現的軟化段特征，本文在定義改進I-M-K 材料模型的軟化段時，根據文獻[15]的方法，定義峰值點位移的下限，如圖5(b)所示。

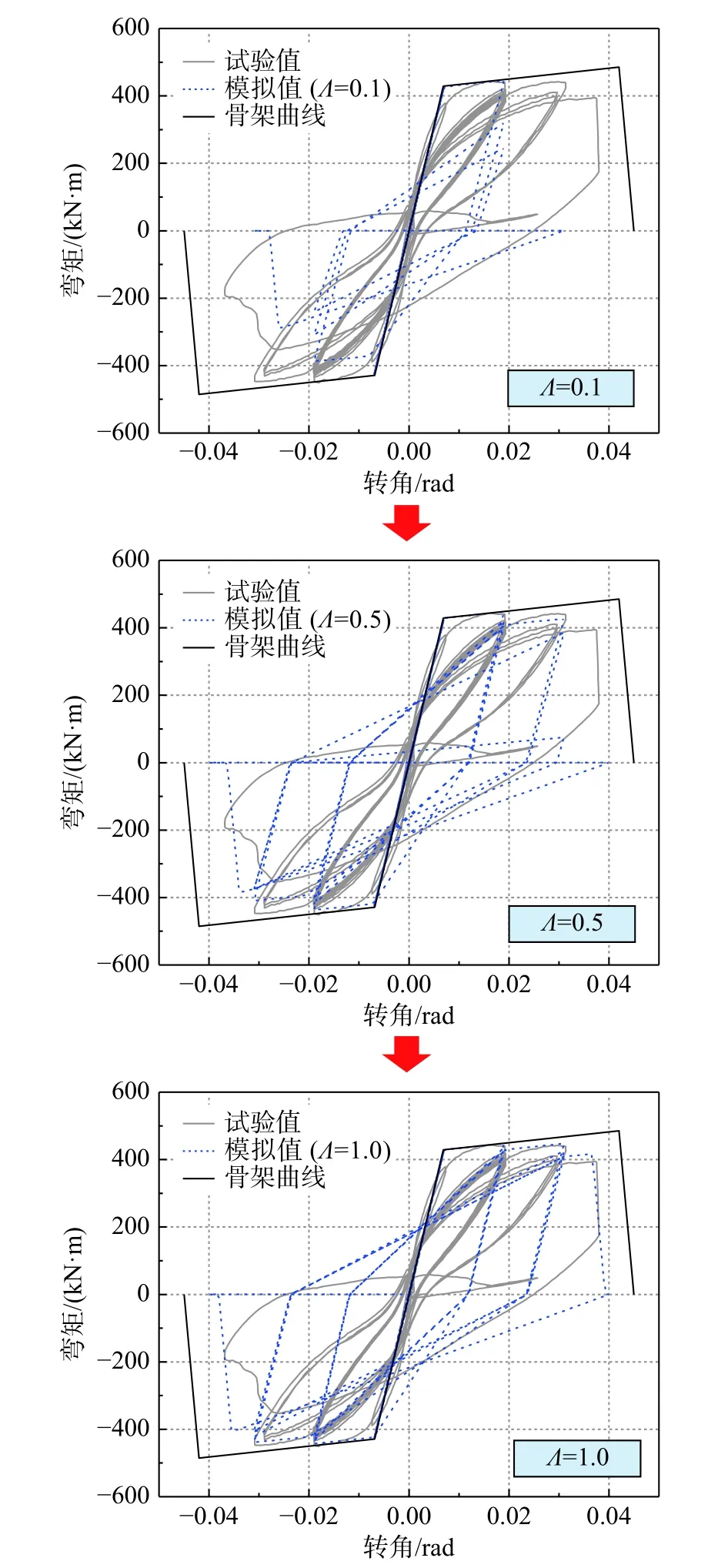
圖 3 對應不同Λ 取值的RC 圓柱滯回模型參數Fig. 3 Hysteresis curves of RC circle columnwith different values of Λ

4 RC 圓柱恢復力模型參數的預測

4.1 預測方程的選擇

在第3 節已獲得的76 根RC 圓柱恢復力模型參數的識別結果基礎上，本節進一步回歸RC 圓柱的恢復力模型參數的預測公式。采用式(1)所示的方程形式來對RC 圓柱的恢復力模型參數進行預測。

4.2 預測方程的擬合流程

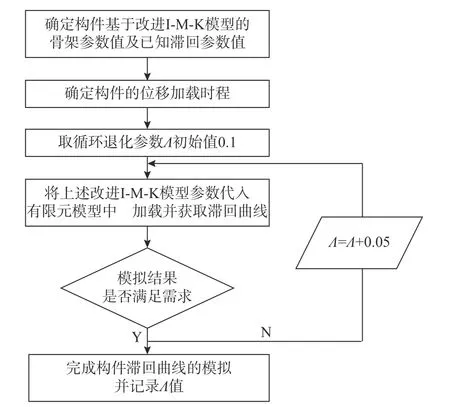
圖 4 參數Λ 的迭代識別過程Fig. 4 Cyclic identification process of Λ

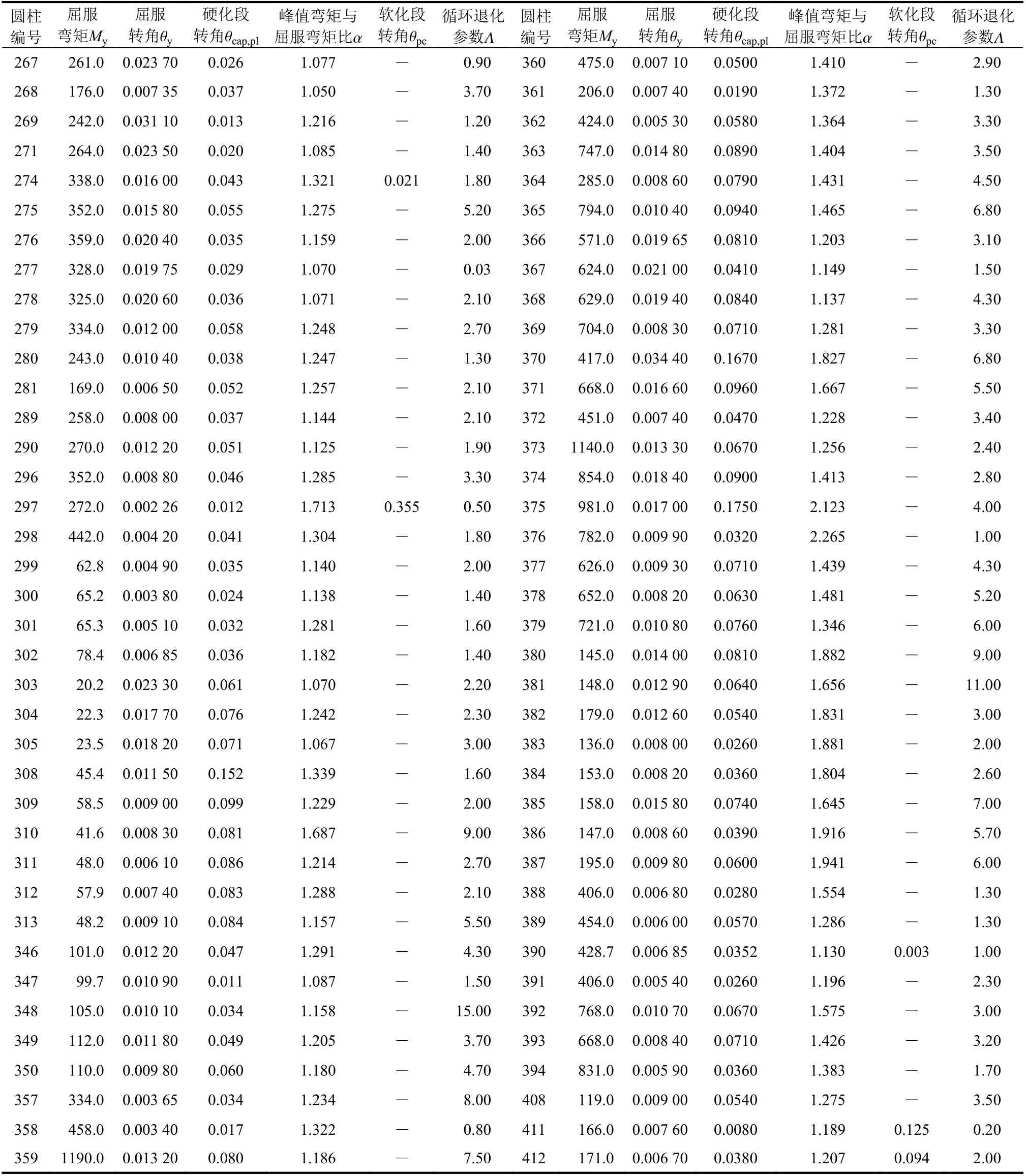
表 3 基于改進I-M-K 材料模型的76 個RC 圓柱的滯回模型參數識別結果Table 3 Identified parameters of modified I-M-K material model for 76 RC circular columns of concern

基于式(2)對RC 圓柱恢復力模型的不同參數分別進行擬合。鑒于所考慮的RC 圓柱15 個設計參數之間可能存在較強相關性，會導致多重共線性問題。因此，在擬合過程中要求其變量之間的方差膨脹因子(Variance Inflation Factor, VIF)小于10。為此，本文采用分步擬合法，對參數進行初選后，采用“只出不進”的方式[19]，通過減少輸入變量，避免各擬合變量之間的多重共線性，關鍵步驟如下：

步驟1：將全部15 個柱設計參數對數化后作為輸入變量，將對數化后的滯回模型參數作為輸出變量，采用式(2)進行初步擬合；

圖 5 典型RC 圓柱的參數識別流程及結果Fig. 5 Identification process and obtained hysteretic model parameters for two typical RC circular columns

步驟2：基于步驟1 中初步擬合結果中15 個輸入變量的p 值，挑選p<0.05 的變量(該變量t 檢驗線性顯著)[19]作為新的輸入變量進行二次擬合；

步驟3：計算二次擬合中各輸入變量的VIF值，若所有輸入變量的VIF≤10[20]，則說明采用二次擬合中的輸入變量擬合公式多重共線性弱，滿足要求。若存在輸入變量的VIF>10，則逐步刪除VIF 最高的輸入變量，直至所有輸入變量VIF≤10；

步驟4：在步驟3 基礎上，為避免過擬合情況，本文在保證公式預測精度的基礎上，刪除了輸出參數相關性較小的輸入參數，以最大程度控制輸入參數數量。待輸入參數確定后，記錄回歸方程的常數項及各變量的回歸系數，完成式(2)形式擬合，隨后將式(2)轉變為式(1)形式，獲得參數的預測公式。

4.3 模型參數的預測公式(值)

基于上文流程可給出預測參數包括屈服彎矩My、屈服轉角θy、硬化段轉角θcap,pl、峰值彎矩與屈服彎矩比a、軟化段轉角θpc，及循環退化參數Λ 的預測公式。需要說明的是，雖然試件識別出的骨架曲線參數在正負方向上顯示出了一定的非對稱性，但不對稱程度并非特別明顯。為簡化起見，本文統一采用了正向的骨架參數值進行公式擬合。

4.3.1 屈服彎矩My

參考第4.2 節的擬合流程對屈服彎矩My進行經驗預測公式擬合，獲得預測公式為：

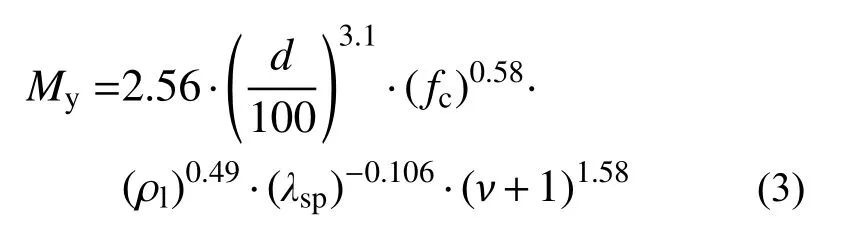
式(3)中各變量的VIF 值，如表4 所示。式(3)的擬合判定系數R2=0.97，表明式(3)的擬合結果較好。

表 4 屈服彎矩My 經驗預測公式中各變量的VIFTable 4 Variable VIFs in the empirical prediction of My

圖6 給出了My預測值與試驗值之間的關系。預測值與試驗值比值的均值為1.01，中位值為0.98。

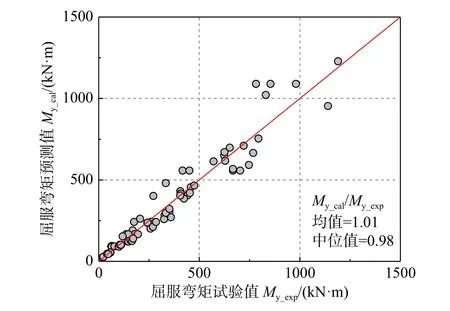
圖 6 屈服彎矩My 的預測值及試驗值對比Fig. 6 Comparison of predicted values andexperimental values of My

4.3.2 屈服轉角 θy

屈服轉角θy的經驗預測公式為：

式(4)中各變量的VIF 如表5 所示，其對應的判定系數為R2=0.475。

表 5 屈服轉角θy 經驗預測公式中各變量的VIFTable 5 Variable VIFs in empirical prediction of θy

圖7 給出了各試件采用式(4)的計算值θy_cal的預測值與試驗值θy_exp與散點對比，可看出二者總體上呈線性關系，隨屈服轉角值提高，離散性逐漸增加，二者比值的均值為1.08，中位值為1.03。

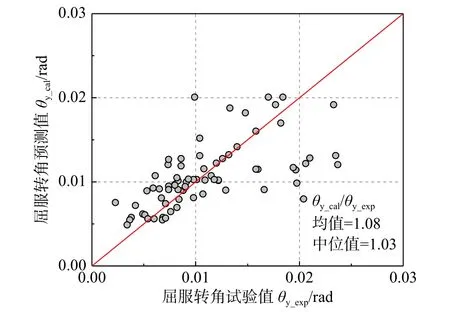
圖 7 屈服轉角θy 的預測值及試驗值對比Fig. 7 Comparison of predicted values and experimental values of θy

4.3.3 硬化段轉角θcap,pl

硬化段轉角θcap,pl的經驗預測公式為：

式(5)中各變量的VIF 如表6 所示。式(5)的判定系數R2=0.452。

表 6 硬化段轉角θcap,pl 經驗預測公式中各變量的VIFTable 6 Variable VIFs in empirical prediction of θcap,pl

圖 8 對比了 θcap,p的預測值 θcap,pl_cal與試驗值θcap,pl_exp。由圖8 可見，多數試驗結果的硬化段轉角小于0.1 rad，預測值與試驗值整體上呈線性關系，二者的比值的均值為1.08，中位值為0.96。

4.3.4 峰值彎矩與屈服彎矩比α

采用式(2)所示的線性方程對α 的預測方程進行擬合，結果表明：α 值與15 個設計參數之間的相關性較差。圖9 為表2 中76 根試件的α 的試驗值，可看出α 的取值總體較為穩定，均值為1.36，標準差為0.26。故本文取平均值1.36 作為α 的經驗計算值。

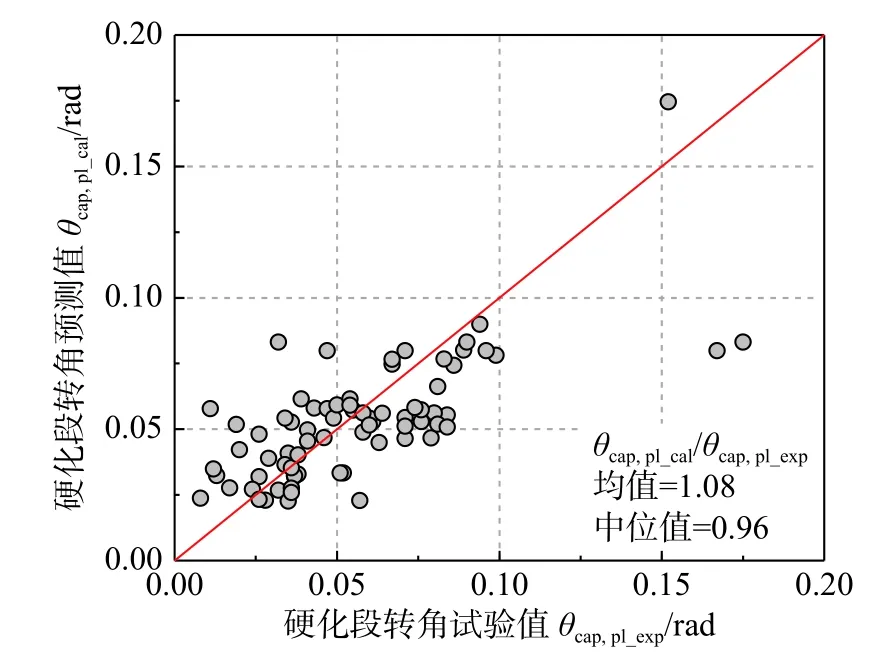
圖 8 硬化段轉角θcap,pl 的預測值及試驗值對比Fig. 8 Comparison of predicted values and experimental values of θcap,pl

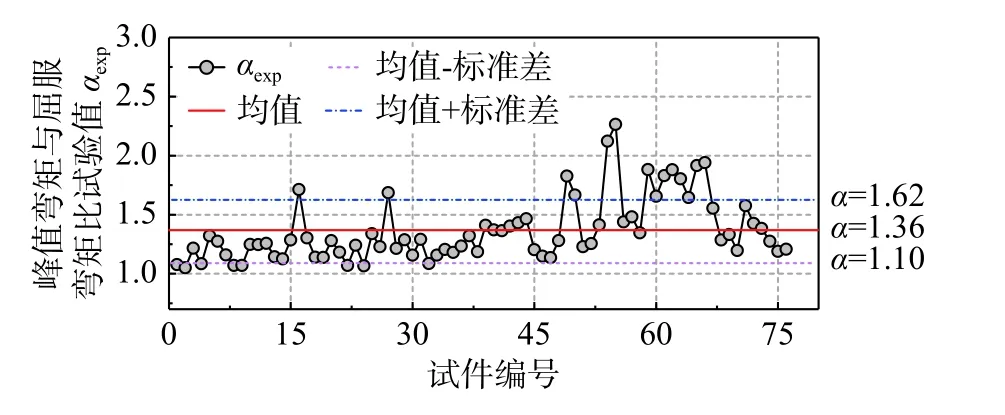
圖 9 76 根RC 圓柱峰值彎矩與屈服彎矩比α 的試驗值Fig. 9 Experimental values of ratios between peak moment and yield moment of 76 RC circular columns

4.3.5 軟化段轉角θpc

由表2 可看出，僅有5 根RC 圓柱試件的恢復力模型參數識別結果包含軟化段轉角，表明RC 圓柱在采用改進I-M-K 材料模擬時硬化段即已達到極限破壞狀態，θpc對后續模擬結果影響很小。因參數識別時必須添加θpc的數值，本文在此建議取表2 中5 根包含軟化段轉角試件θpc的平均值0.13 rad，這一結論與文獻[9]和文獻[15]研究方柱恢復力模型時的結果(θpc=0.1 rad)較為接近。

4.3.6 滯回耗能參數Λ

滯回耗能參數Λ 的經驗預測公式為：

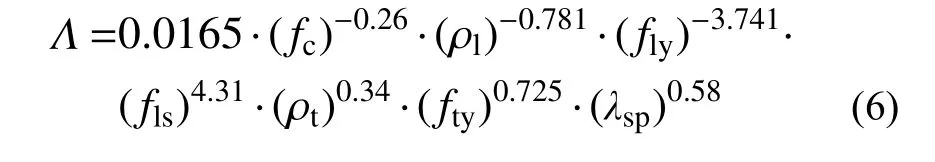
式(6)中各變量的VIF 如表7 所示，其對應的判定系數R2=0.41。

表 7 滯回耗能參數Λ 經驗預測公式中各變量的VIFTable 7 VIF of variables in empirical prediction of Λ

圖10 為各試件采用式(6)的得到的Λ 計算值Λcal與試驗值Λexp對比結果。由圖可見，試件的Λ 值介于0～10 之間，這一范圍大于文獻[13]中Λ的取值范圍。主要原因為，本文研究的RC 圓柱中部分試件的耗能能力較強。此外，預測值略大于試驗值，二者比值的均值為1.09，中位值為0.98。

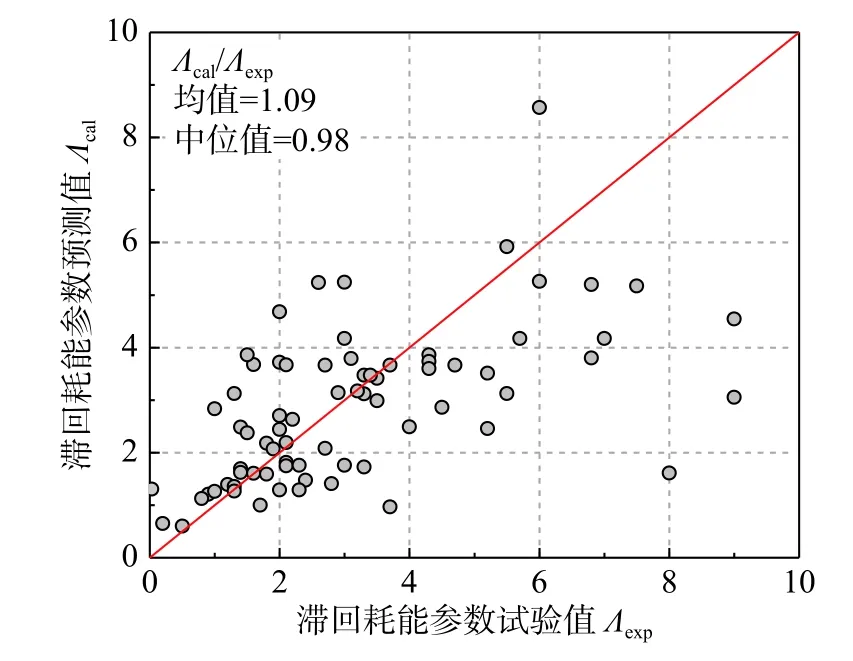
圖 10 滯回耗能參數Λ 的預測值及試驗值對比Fig. 10 Comparison of predicted values and experimental values of Λ

5 RC 圓柱恢復力模型參數的驗證

為驗證第3 節中給出的RC 圓柱恢復力模型經驗預測公式及經驗值的合理性，本文以文獻[21]中試件A12、文獻[22]中試件CA-1 及文獻[23]中的試件RC3 作為驗證組試件對本文識別獲得的恢復力模型進行驗證。上述三個RC 圓柱構件并未包含進入本文的試驗數據庫，因此，用其作為驗證組不會出現“數據泄露”的問題。

表8 給出了驗證組圓柱試件的基本設計參數，其失效模式均為彎曲破壞。基于第4.3 節獲得的RC 圓柱恢復力模型參數的預測公式，結合參照組RC 圓柱試件的設計參數(表8)，計算得到參照組RC 圓柱恢復力模型參數的計算值，如表9 所示。基于所獲得的參照組RC 圓柱恢復力模型參數的計算值，獲得驗證組柱試件的滯回曲線，并將其與試驗結果進行對比，如圖11 所示。由圖11可見，基于本文提出的經驗公式的模擬結果與試驗結果具有較高的吻合程度。考慮驗證組試件在直徑、混凝土強度、配筋率、軸壓比等重要設計參數的差異性，本文提出的基于改進I-M-K 材料模型的恢復力模型參數預測方程可準確的預測出RC 圓柱試件在不同設計工況下滯回曲線的強度值及滯回特征的變化規律。

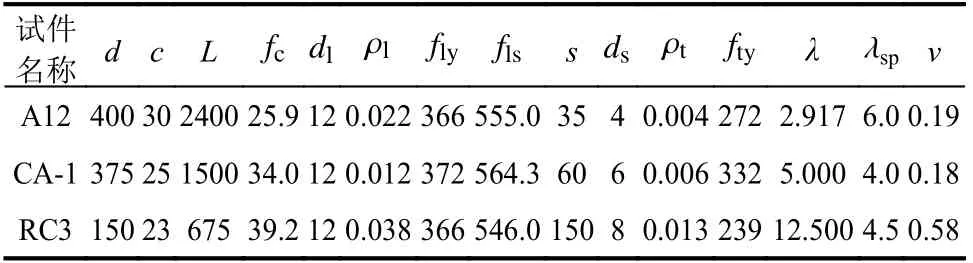
表 8 驗證組柱試件的設計參數Table 8 Design parameters of column specimens in verification group

表 9 驗證組柱試件基于經驗公式的改進I-M-K 參數計算值Table 9 Calculation results of modified I-M-K parameters based on empirical equations

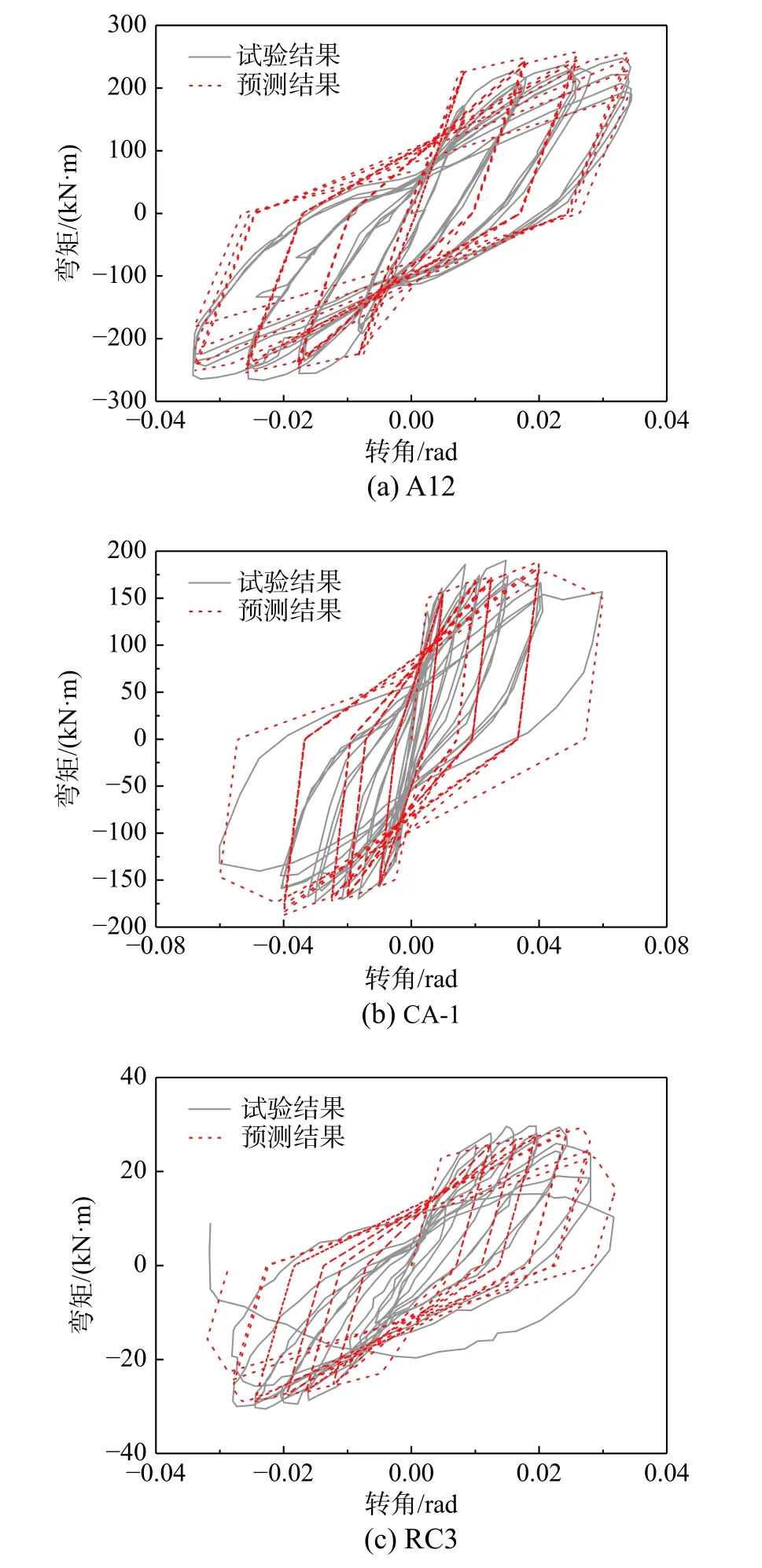
圖 11 驗證組試件試驗與模擬結果對比Fig. 11 Comparison of test and simulation results of column specimens in verification group

6 結論

本文基于PEER 結構性能數據庫中76 個RC圓柱滯回試驗數據，基于改進I-M-K 材料模型，利用OpenSEES 有限元平臺，對RC 圓柱的恢復力模型參數進行識別，并獲得滯回模型骨架參數及滯回耗能參數的預測方程。本文結論如下：

(1) 本文提出的方法可以較好地識別出RC 圓柱的恢復力模型參數。基于所識別出的改進I-M-K恢復力模型可以很好地模擬RC 圓柱在滯回加載過程中的強度及剛度退化特征；

(2) 在對數坐標系下，采用多元線性回歸方程可很好的擬合出屈服彎矩My、屈服轉角θy、硬化段轉角θcap,pl、滯回耗能參數Λ 的經驗預測公式。其中屈服彎矩My擬合精度最好，其判定系數為0.97；

(3) 峰值彎矩與屈服彎矩比α 的取值與設計參數無明顯關聯，本文研究推薦取所有試件的平均值1.36。絕大部分試件的參數識別結果不含軟化段轉角θpc，本文研究推薦取可校準出θpc段的試件的平均值0.13 rad；

(4) 對比基于本文經驗公式得到的對照組試件滯回曲線及試驗滯回曲線，可看出，本文提出的RC 圓柱經驗公式/經驗值可很好的預測出RC 圓柱的在滯回循環中的強度值及滯回特征變化。

值得指出的是，本文所采用的鋼筋混凝土圓柱試件的失效模式均為彎曲破壞或彎剪破壞。因此，本文所提出的恢復力模型僅適用于彎曲破壞和彎剪破壞的鋼筋混凝土圓柱。由于失效模式為剪切破壞的鋼筋混凝土柱的滯回性能與彎曲破壞或彎剪破壞柱的滯回性能差異性較大，因此，本文所提出的恢復力模型并不適用于剪切破壞圓柱。