基于區間對偶猶豫模糊語言變量的VR在線購房顧客需求分析
程紫薇,楊志輝,王斌斌
(東華理工大學理學院,江西 南昌 330013)
隨著VR技術的到來與發展,給生活的諸多方面帶來了便捷,VR看房產業應運而生。通過立體眼鏡、數據手套結合的特制傳感裝置,顧客將直面三維的模擬現實,不用親臨樓盤現場,也能通過人的自然技能和相應的設施進行信息交互,使顧客挑房買房更加便捷。例如,顧客能通過VR實景了解房屋配套設施、地段、物業管理、環境等,并根據自身所需做出相應決策。
在民生問題的復雜性前提下,顧客需求會隨著年齡、職業、家庭、環境等因素的變化而變化,在顧客給出需求測度時可能會存在模糊性的情況,這種模糊性很大程度會影響后續的工程特性。為刻畫模糊性現象,美國控制論專家Zadeh[1]教授通過將經典集合的特征函數拓展為隸屬函數,提出了模糊集的概念。隨著模糊集的發展,諸多不足被日益完善,例如學者們在模糊集基礎上拓展出直覺模糊集[2]、猶豫模糊集[3]、對偶猶豫模糊集[4]等,以描述生活中眾多亦此亦彼的模糊性現象。作為模糊集的一種有效拓展,Bahram[5]在對偶猶豫模糊集基礎上提出區間對偶猶豫模糊集。
由于Zhu[4]提出的對偶猶豫模糊語言集隸屬度與非隸屬度取值為[0,1]上若干個數組成的集合,Bahram將其與區間數理論結合,拓展出了區間對偶猶豫模糊語言集。由于隸屬度與非隸屬度的完整性,使其能更準確的表達決策者的猶豫不決,解決了實際問題的復雜不確定性。因此,學者們紛紛探究其在多屬性決策中的應用。
相比較其他算子而言,在處理多屬性決策問題時,由于Frank算子可以根據不同的參數來解決不同類型的多屬性決策問題,具有較強的兼容性。目前,關于Frank算子應用于區間對偶猶豫模糊語言變量還比較少見,因此,區間對偶猶豫模糊語言Frank集成算子具有重要的研究意義。
首先,基于區間對偶猶豫模糊語言環境下的運算規則、得分函數、精確函數和大小比較方法,定義了區間對偶猶豫模糊語言環境下Frank算子的運算規則,提出了區間對偶猶豫模糊語言Frank加權算術平均算子、對偶猶豫模糊語言Frank有序加權算術平均算子,研究了這些算子的有界性、單調性等性質,并證明參數θ逼近1時,區間對偶猶豫模糊語言Frank加權算術平均算子退化為區間對偶猶豫模糊語言加權算術平均算子。最后,將區間對偶猶豫模糊語言Frank加權算術平均算子應用于區間對偶猶豫模糊語言環境下的VR在線購房顧客需求問題研究。
1 預備知識

(1)
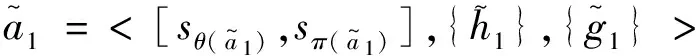
(1)數乘運算
(2)
(2)冪運算
(3)
(3)和運算
(4)
(4)積運算
(5)
在研究區間對偶猶豫模糊語言變量時,得分函數和精確函數能有效解決其大小比較問題。由于原有的得分函數存在一定的不足,沒有考慮區間對偶猶豫模糊元中隸屬度與非隸屬度與其均值的偏差大小。因此,本文結合最小二乘法思想,重新定義得分與精確函數。

(6)
(7)
基于區間對偶猶豫模糊語言變量的得分函數和精確函數,有下列大小比較規則。
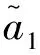
定義5[16]對于任意兩個的實數a,b,θ>1,Frank-T范數和Frank-S范數定義分別如下
(8)
(9)
2 區間對偶猶豫模糊語言Frank集成算子
2.1 區間對偶猶豫模糊語言Frank算子的運算規則
定義區間對偶猶豫模糊語言環境下Frank算子的運算法則如下
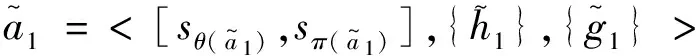
(1)數乘運算
(10)
(2)冪運算
(11)
(3)和運算
(12)
(4)積運算
(13)
易證上述計算結果仍為區間對偶猶豫模糊語言變量。為了實現多個區間對偶猶豫模糊語言變量的集結,本文提出了基于區間對偶猶豫模糊語言集的加權算術平均算子、有序加權算術平均算子。
2.2 區間對偶猶豫模糊語言Frank加權算術平均算子
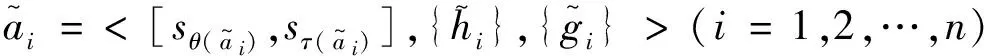
(14)
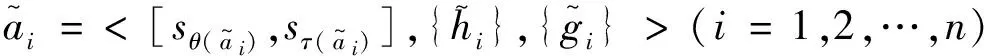
(15)
證明下面將通過數學歸納法證明等式(15)成立。當n=2時
假設當n=k時,則有
那么,當n=k+1時,有
可以證明IDHFLFWA算子具有有界性,如定理2所示。
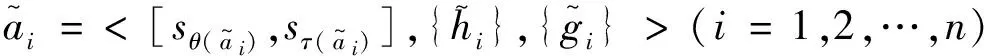
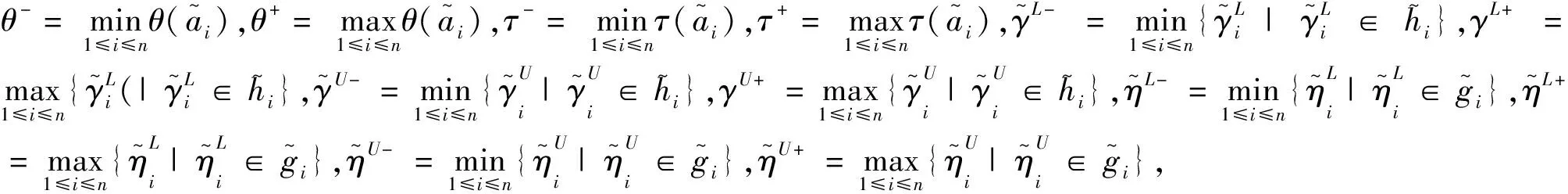
則
由定義7、定義8,可得
同理,由定義7、定義8,可得
綜上所述,有
即證。
此外,易知IDHFLFWA也算子具有單調性,如定理3所示。
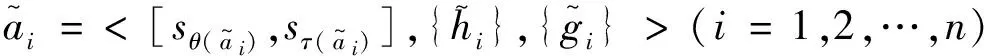
下面研究IDHFLFWA算子中參數θ的性質。
推論1當θ→1時,區間對偶猶豫模糊語言Frank加權算術平均算子(IDHFLFWA)退化為區間對偶猶豫模糊語言加權算術平均算子(IDHFLWAA):
證明由定義6可得

可以得到

2.3 區間對偶猶豫模糊語言Frank有序加權算術平均算子
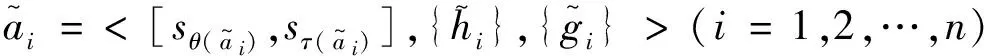
顯然,與區間對偶猶豫模糊語言Frank加權算術平均算子類似,區間對偶猶豫模糊語言Frank有序加權算術平均算子也具有有界性和單調性。
3 基于區間對偶猶豫模糊語言Frank集成算子的決策方法及步驟
此前,有關模糊集的研究已應用于顧客需求的研究中,但大多數案例使用了傳統的模糊多屬性決策方法。相比之下,區間對偶猶豫模糊語言在描述顧客需求時,比其他模糊語言另具有猶豫性,能更客觀描述顧客需求;此外,區間對偶猶豫模糊語言Frank集結算子含有參數θ,顧客可根據具體決策問題相應地改變參數θ的取值,使得區間對偶猶豫模糊語言Frank集結算子比其他算子更具靈活性。

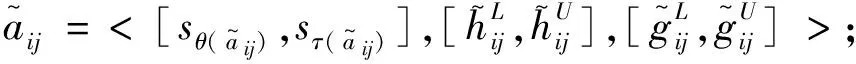
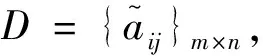

步驟4根據定義8,對各個備選方案進行綜合性能的排序。得分函數值越大,方案的性能值越好;當得分函數值相等時,繼續比較精確函數值,精確函數值越大,方案性能越好,以此選出最優方案。
4 實證分析
某房產公司采用了高科技數字一體化售樓機制,主要體現在VR在線看房、影視宣傳片、三維動畫宣傳片、互動多媒體展覽展示等業務,尤其是VR虛擬現實業務,使看房顧客在VR大廳就能使用人的自然技能和相應的設施進行信息交互,獲取樓盤所有相關信息。針對VR看房系統,經過前期試營業,挑選關注度較高的四個顧客需求測度:
A1:地理位置(包括城市定位、交通等)
A2:配套設施(包括教育、醫療、物管、購物、娛樂等)
A3:房屋設計(包括房產面積、戶型、樓層等)
A4:房價(包括房產單價、是否保值或升值,尤其考慮購房目的是住家或投資等)
由于購房顧客的生活背景、年齡、購房目的等原因,對上述四個需求會有不同的考慮,故隨機在VR大廳挑選了一批顧客,通過問卷調查形式收集顧客基本信息和購房需求,收集整理后將購房顧客按性別、年齡、收入等聚類分析,大致分為4類具有代表性的顧客問卷,分別為C1公職人員、C2個體戶、C3務農者、C4退休者。由于問卷數量較大,事先通過主成分分析,挑選出具有代表性的問卷結果,再由相關專家對其問卷進行評估。
為更好的保留顧客需求的原始信息,專家均采用區間對偶猶豫模糊語言對顧客需求進行表示,屬性權重向量為ω=(0.35,0.3,0.15,0.2),語言評價集為
整理后的具體評分表如表1所示。

表1 各顧客需求的屬性值
步驟1由于4個顧客需求均為效益型屬性,因此無需進行規范化處理。
步驟2運用區間對偶猶豫模糊語言Frank加權算術平均算子(IDHFLFWA)對屬性信息進行集成。由于區間對偶猶豫模糊語言Frank加權算術平均算子(IDHFLFWA)形式會隨參數而變,為了更好的選擇備選方案,本文將列舉3個具有代表性的參數值分別進行計算,其中θ=1.1,θ=2和θ=20。
步驟3計算各個備選方案綜合屬性值的得分函數值。
(1)當θ=1.1時,有
(2)當θ=2時,有
(3)當θ=20時,有
步驟4根據定義8,對各個方案進行排序,排序結果都為A2?A4?A1?A3。這一結果表明,顧客有初步購房需求,并且對房屋有初步了解,說明有一定的經濟基礎,因此其他因素會是重要考慮。如上班族為了便于上班,會多關注房屋地理位置;居家者為了方便孩子上學與日常生活,會更關注樓盤周邊學區等配套設施。但綜合考慮,利用區間對偶猶豫模糊語言算子進行計算時,取不同參數值θ都有A2?A4?A1?A3,可得A2房屋配套設施為顧客需求中最受關注的,因此房產公司可加大這方面的設置與宣傳,滿足多層次顧客所需。
為了進一步說明本文提出的算法具有可靠性、合理性,下面將與文獻[7]中提出的區間對偶猶豫模糊語言加權幾何平均算子(IDHFLWAA)進行對比分析。具體決策過程與本文提出的區間對偶猶豫模糊語言Frank加權算術平均算子(IDHFLFWA)類似,得到的結果如表2所示。
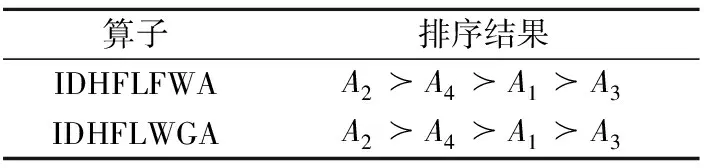
表2 利用不同算子計算得到的排序結果
通過觀察表2中的排序結果可以發現,運用兩種不同的算子計算得到的排序結果相同:A2?A4?A1?A3,即顧客需求測度最高的都為A2,可知A2房屋配套設施為最受關注的顧客需求,說明本文構建的多屬性決策方法具有合理性。此外,本文提出的區間對偶猶豫模糊語言Frank加權算術平均算子(IDHFLFWA)和區間對偶猶豫模糊語言Frank加權幾何平均算子(IDHFLFWG)具有可變參數θ,這將能滿足決策者的不同偏好,使得決策過程更靈活多變,因此決策更具一般性。本文提出區間對偶猶豫模糊語言Frank集結算子是有效且靈活的。
5 小結
本文基于語言評價集、區間值對偶猶豫模糊集,提出了改進的得分函數和精確函數。再結合FrankS-范數與FrankT-范數,給出了區間對偶猶豫模糊語言變量Frank集結算子,即區間對偶猶豫模糊語言Frank加權算術平均算子、區間對偶猶豫模糊語言Frank有序加權算術平均算子,并對兩種算子的有界性、冪等性、單調性和交換性等性質加以研究。之后,給出了區間對偶猶豫模糊語言Frank集結算子具體的決策步驟,將區間對偶猶豫模糊語言Frank加權算術平均算子應用于多屬性決策問題。最后,通過實例并與文獻[6]中提出的區間對偶猶豫迷糊語言加權幾何平均算子做對比分析,表明本文提出的對偶猶豫模糊語言Frank集結算子具有可行性和有效性。

