函數y=Asin(ωx+φ)性質的應用

江蘇省泰州中學 (225300) 宋 健

關于函數y=Asin(ωx+φ)的圖像和性質是三角知識的一個重要節點，從函數知識方面來說就是一個高點，關注與此有關的綜合問題有助于全面理解課本知識體系，站在新的高度檢驗對這些知識點的掌握程度，本文通過分析幾類典型題例的求解方法，展示此類問題的解題方案，務求給讀者朋友有所幫助．

一、識圖像 重應用

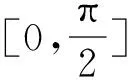
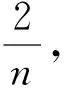
二、先轉化 再化歸

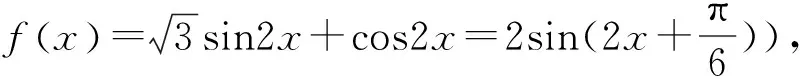
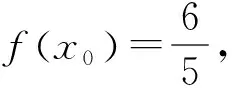
評注：這一類典型題目的解法是利用三角公式化簡，將函數轉化為y=Asin(ωx+φ)的形式，然后根據三角函數在特定區間上的有界性求出函數的最大值和最小值．

三、抓特點 定參數

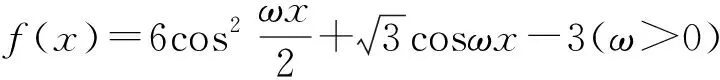
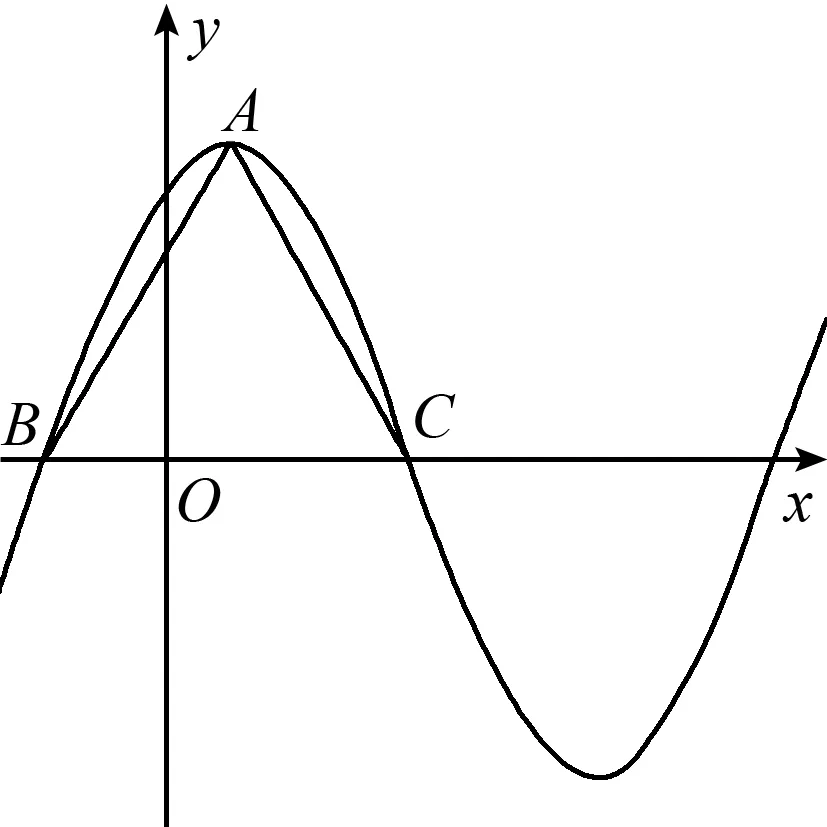
圖1

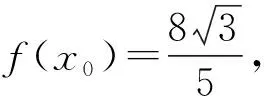
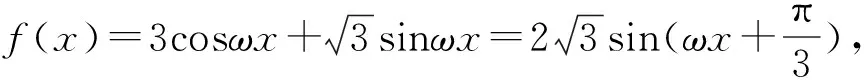
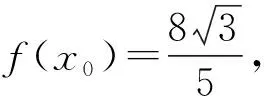
評注：在函數y=Asin(ωx+φ)中，如何根據已知條件確定其中的參數A、ω、φ，也是一類常見問題，這里必須抓住特點、精巧列式，本題中由正三角形的剖析是解題關鍵．

四、用性質 建方程

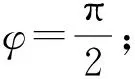
評注：本題的解決實際上是抓住兩個對稱性列方程、解方程的過程，由于三角函數有多值的特點，故需對參數k分類討論，然后再逐個驗證后確定，否則可能出現增解或漏解．

五、擬函數 再運用

例5 某港口水的深度y(m)是時間t(0≤t≤24，單位：h)的函數，記作y=f(t)，下表是某日的水深數據.

t03691215182124y10.013.09.97.010.013.010.17.010.0

經長期觀察，這組數據比較穩定.(1)試根據以上數據，擬合函數擬合函數的近似表達式；(2)一般情況下，船舶航行時，船底離海底的距離為5 m或5 m以上被記為是安全的(船舶停靠時只需不碰海底即可)，某船吃水深度(船底離水平面的距離)為6.5 m，如果該船希望在同一天內安全進出港口，那么它至多能在港內停留多久？(忽略進出港所需時間)

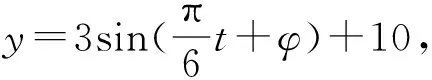
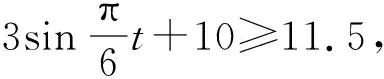
評注：本題是一個實際生活中的應用問題，由列表數據分析可得對應的函數圖像是一個正弦曲線，抓住這個重要信息，擬合出函數解析式，為后面的實際問題的解決創造了條件．

六、綜合題 抓主線

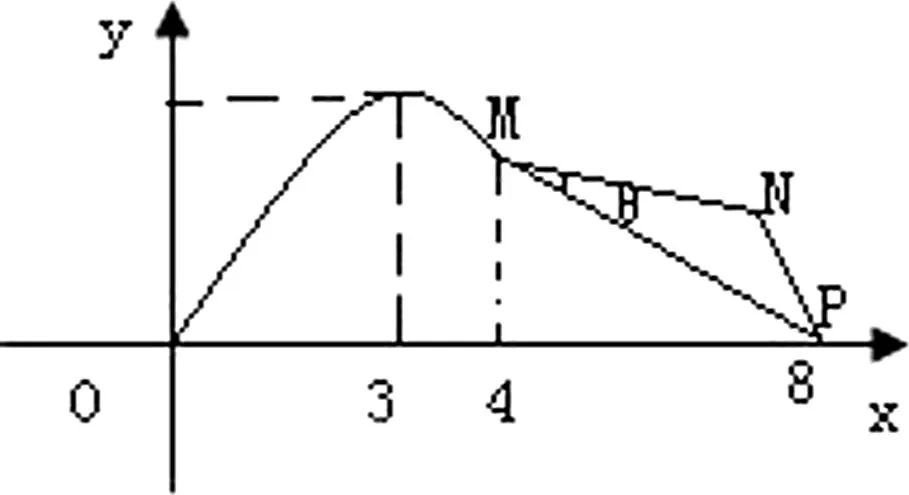
圖2

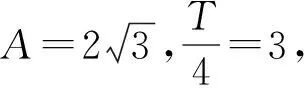
評注：本題是一道綜合應用問題，先運用所給數據確定函數表達式，解決了關鍵的線段MP的長，然后再通過設∠PMN=θ，由正弦定理列式，建立了折線段賽道MNP的函數式，運用三角函數的有界性解決了最值問題，這就是此類題的求解主線．