復合管道超聲波流量傳感器設計
馮旭東,楊瀟楠,姜雪,馮毓涵
(西安石油大學,陜西西安,710065)
0 引言
火電廠使用循環的石膏漿液進行煙氣脫硫處理,漿液流量是評價脫硫系統效率的重要參數,但漿液流量卻不易檢測,由于漿液是含有固體顆粒的腐蝕性液體,必須采用抗腐蝕的橡膠內襯復合管道輸送,在不影響生產的情況下采用接觸式流量計是不現實的,常見的非接觸式的超聲波管道流量計只能用于碳鋼材料的管道,根本原因是其匹配的傳感器無法適用于復合管道,本文針對適合復合管道中漿液的流量檢測的傳感器進行研究,設計了一種基于多普勒流量測量原理超聲波傳感器,采用收發一體式封裝,安裝簡便,通過敏感元件(材料)的選取、參數設計、結構設計提高傳感器對復合管道的適用性,傳感器室內試驗中能夠在復合管道流體中采集到含有流量信息的超聲波信號,與匹配檢測系統可以實現對復合管道的流量檢測并取得較好的效果。同時,傳感器也適用于普通碳鋼管道中流體的流量測量。
1 敏感元件
敏感元件是指在傳感器中能夠直接感受或者響應被測物理量的元件,它是傳感器的核心[1]。用于流量檢測的超聲波傳感器的敏感元件一般為壓電陶瓷,壓電陶瓷具有靈敏度高、溫度特性好、易于加工等優點,被廣泛的使用于各種超聲波檢測中[2]。復合管道比一般的碳鋼管道多了內襯橡膠層,在傳感器敏感元件的選取上要求會更為嚴格,本設計采用鋯鈦酸鉛壓電陶瓷(PZT)中的PZT–5作為傳感器敏感元件,相比其他的壓電陶瓷材料,PZT–5的壓電常數高,可以獲得很高的發射和接收靈敏度,同時機械品質因子最低,可以獲得高分辨率和很小的盲區,十分適合復合管道。
2 參數設計
復合管道中的漿液含有固體顆粒,適合采用多普勒測量方式,因此,傳感器的工作頻率和靈敏度這兩個參數非常重要。
(1)工作頻率設計
傳感器工作頻率設計應滿足多普勒測量方式的要求,即超聲波必須有散射回波,否則無法接收到回波信號[3]。按照超聲波的衰減理論,只有散射衰減才能形成散射回波,而散射的形成與超聲波的波長及固體顆粒的尺寸密切相關[4]。圖1為散射聲場示意圖,圖中λ為超聲波波長,2a為固體顆粒直徑。
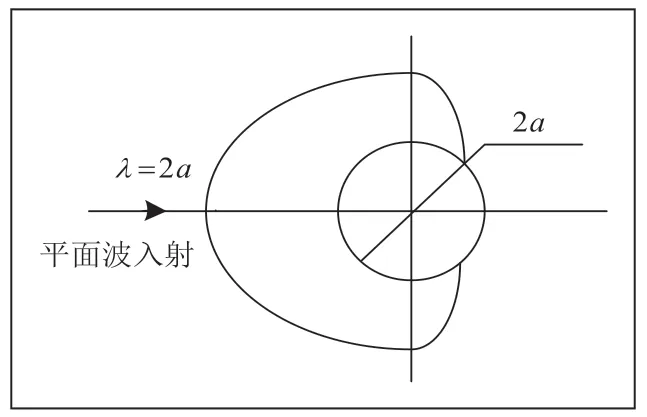
圖1 散射聲場示意圖
當λ? 2a時,超聲波繞射前行,基本不會有散射回波。當超聲波波長λ與顆粒直徑 2a的比值減小到一定程度時,會逐漸形成散射聲場,當λ≈2a時,會產生多種不同的散射聲場,當λ<2a時,顆粒主要作為反射體,超聲波會被反射,但反射過多會導致波的穿透能力降低,或只能傳播到流體介質淺層界面,不能完整表征管內流速信息[5]。所以,超聲波頻率設計要同時考慮的散射強度和在流體中的穿透深度。綜上所述,傳感器的工作波長應選在λ>2a范圍,同時又不能過大。依據理論計算以及試驗分析,傳感器的工作頻率設計為640kHz。
(2)靈敏度設計
靈敏度是接收傳感器的一個重要指標,實際的應用中多使用電壓靈敏度。電壓靈敏度指傳感器的輸出電壓和聲場里引入傳感器之前這一點的自由聲場電壓的比,一般使用分貝來表示[6],如式(1)所示。
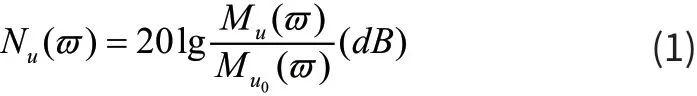
3 結構設計
傳感器采用發射與接收一體式結構設計,主要由敏感元件、聲楔塊、阻尼層、匹配阻抗、保護外殼組成。其中敏感元件采用PZT–5,其直徑為20mm,厚度2mm,聲楔采用有機玻璃,阻尼層為硅膠及鎢粉混合物,保護外殼為鋁合金材質,整體密封,其結構示意圖如圖2所示。這種結構設計避免了分離的傳感器由于安裝位置。
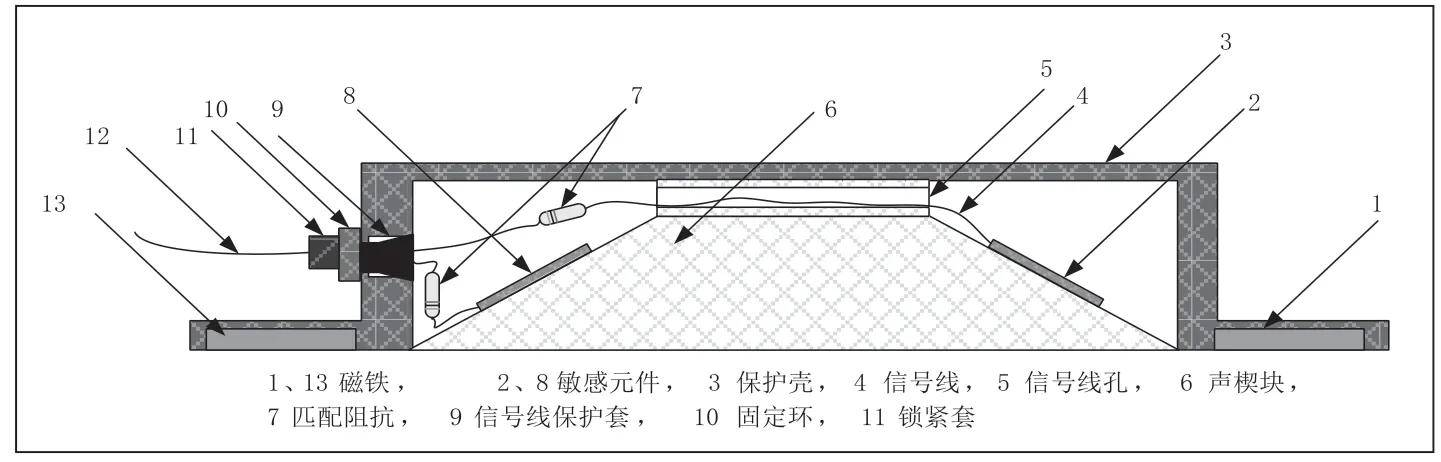
圖2 傳感器結構示意圖
不合適而導致測量精度下降。聲楔塊為等腰梯形結構,底角的角度是33.5°,這個設計是通過理論計算和試驗得到的,有效抑制了超聲波在管道和流體中傳播時產生較強的交互回響[7]。聲楔塊的兩個斜面光滑平整,使用環氧樹脂雙組份按4:1比例混合后將兩片陶瓷片分別緊密貼合在聲楔塊斜面上,環氧樹脂作為匹配層可以使聲波從PZT陶瓷片入射到聲楔時的投射系數得到提高[8]。兩片壓電陶瓷片的正,負極在同一側,焊接導線后連接阻抗元件以匹配檢測電路。使用704硅橡膠參入定量鎢粉均勻混合后作為阻尼層涂抹在整個聲楔斜面上將壓電陶瓷片密封固化,厚度約為2mm。硅橡膠為高阻抗、高衰減的吸聲材料,可以吸收壓電陶瓷片背面輻射的超聲波干擾[9]。最后,將密封好壓電陶瓷片的聲楔斜塊完整放入鋁合金保護外殼,聲楔斜塊放入外殼后其平面與外殼平面一致,保護殼留有電纜線孔,傳感器的信號輸出使用TNC接頭,電纜線采用雙重屏蔽電纜以降低噪聲對接收信號的干擾。
4 性能試驗
利用室內流量試驗平臺對傳感器的性能進行試驗,通過試驗檢測傳感器能否匹配測量電路在復合管道上有效發射和接收超聲波信號以及在不同流速下的實際測量情況。試驗平臺主要由管道泵、質量流量計、復合管道(管道內徑為50mm)、變頻器、儲液罐組成,流體介質使用石膏粉和水按一定比例配置模擬漿液。試驗時將兩只傳感器分別安裝在復合管道和普通管道上,管道泵驅動模擬漿液在管道中保持穩定循環,通過變頻器可調節管道泵的轉數以改變漿液流速,流體的實際流量值可通過質量流量計(±0.1%)測得。試驗中可以監測傳感器的發射和接收的信號,示波器采集到的發射信號和接收信號如圖3和圖4所示。試驗后整理的數據如表1所示。
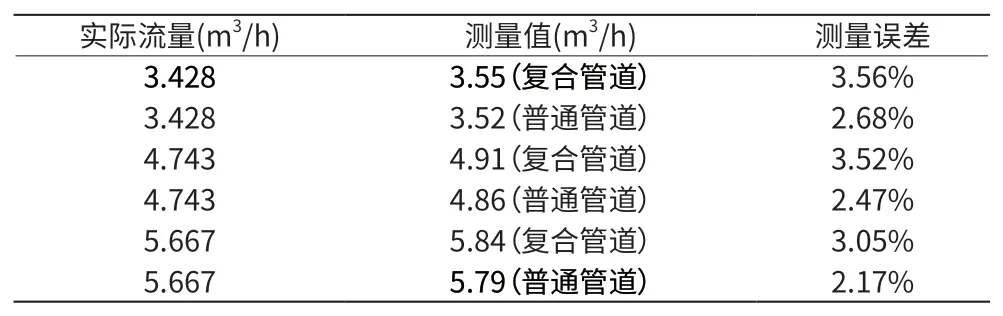
表1 三種流量的測量值及誤差
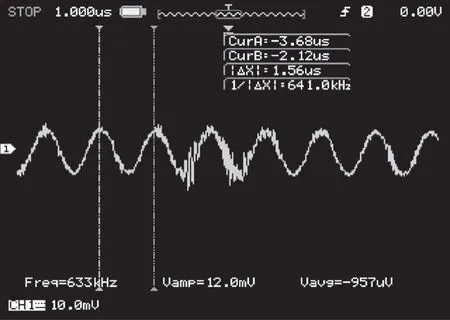
圖4 傳感器接收信號波形圖
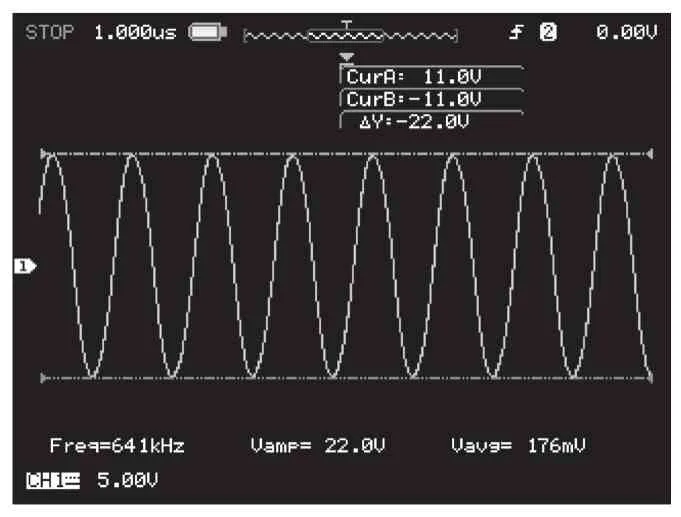
?
試驗表明:傳感器能夠與匹配檢測系統實現了復合管道的流量檢測,總體誤差低于5%,隨著流量的增加,檢測精度有所提高,而實際流量要高于試驗時流量,因此,傳感器不僅可以滿足實際要求,適用性也更為廣泛。
5 結論
本文對復合管道的流量檢測傳感器技術進行了研究,基于超聲波多普勒測量方法對傳感器的敏感元件、關鍵參數、結構等方面進行了探索性設計,取得了較好的試驗效果,驗證了技術可行性,對超聲技術在復合管道流量檢測中的應用具有參考價值。

