焊管生產線開卷機齒輪機構瞬態動力學分析*

楊佩東

（山西工程職業學院， 太原030009）

開卷機是焊管生產線的重要設備之一， 其主要作用是通過漲緊鋼卷內孔來支撐住鋼卷，并通過旋轉將鋼帶頭部送入矯平機中。 旋轉運動主要是通過變頻調速電機連接齒輪箱減速后驅動卷筒軸， 從而為開卷機提供動力。 齒輪機構在開卷機扭矩傳遞過程中有重要的作用， 它依靠輪齒齒廓直接接觸來傳遞空間任意兩軸間的運動和動力， 具有傳遞功率范圍大、 傳動效率高、 傳動比準確、 使用壽命長、 工作可靠等優點， 在實際工程中得到了廣泛應用。 開卷機齒輪箱在實際使用過程中， 齒輪經常會出現斷齒、 齒面磨損、 齒面膠合等失效現象， 所以對開卷機齒輪機構進行瞬態動力學分析具有重要意義。

1 開卷機齒輪三維建模

目前工程上建立三維模型的軟件有很多種，例如UG、 SolidWorks、 CATIA、 Pro/E 等。 齒輪三維模型的建立可以直接通過三維軟件進行建模， 也可以通過齒輪插件GearTrax 進行建立，或利用專業齒輪設計軟件KISSsoft 進行建模。本研究以某公司開卷機齒輪機構為研究對象， 采用SolidWorks 中Toolbox 插件進行建模， 只需輸入齒輪相應的參數值， 軟件便會自動生成相應的齒輪， 齒輪的基本參數見表1， 其中齒輪1 為從動輪， 齒輪2 為主動輪。

表1 開卷機齒輪的基本參數

一對漸開線齒輪正確嚙合的條件是兩輪的模數和壓力角分別相等， 所以在建立齒輪三維模型時， 將其模數和壓力角設為相同。 齒輪在嚙合傳動時， 為了避免一輪的齒頂與另一輪的齒槽底部以及齒根過渡曲線部分相抵觸， 并留有一定空隙以便儲存潤滑油， 所以兩齒輪在裝配過程中， 一輪的齒頂圓與另一輪的齒根圓之間應當留有一定的間隙， 稱為頂隙。 當頂隙為標準值時， 兩齒輪的中心距依據公式（1） 進行確定[1]。

式中： a——齒輪中心距， mm；

r1、 r2——兩輪分度圓半徑， mm；

m——模數；

z1、 z2——兩輪齒數。

通過公式 （1） 計算得出開卷機齒輪中心距為175 mm， 并在SolidWorks 裝配模式下進行裝配齒輪， 裝配后的齒輪嚙合三維模型如圖1 所示。

圖1 齒輪嚙合三維模型

2 齒輪瞬態動力學分析

2.1 瞬態動力學理論

瞬態動力學是用來分析結構在隨時間任意變化的載荷作用下， 動力響應過程的技術。 在ANSYS Workbench 中， 使用Transient Structural模塊進行瞬態動力學分析， 瞬態動力學的基本運動方程[2-3]為

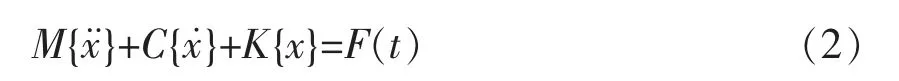
式中： M——質量矩陣；

C——阻尼矩陣；

K——剛度矩陣；

{x¨}——節點加速度向量；

{x˙}——點速度向量；

{x} ——節點位移向量。

2.2 材料性能

常見的齒輪失效形式有輪齒折斷、 齒面磨損、 齒面點蝕以及塑性變形等。 為了避免齒輪失效， 對齒輪材料性能的基本要求為： 齒面要硬、齒芯要韌。 常用的齒輪材料有鋼、 鑄鐵和非金屬材料等， 由于鋼材的韌性好， 耐沖擊， 還可以通過熱處理或化學熱處理來改善其力學性能以及提高齒面硬度， 所以工程上通常使用鋼材來制造齒輪。 本研究所采用的齒輪材料為45 鋼， 其力學性能見表2。

表2 45 鋼的力學性能

2.3 網格劃分

在ANSYS Workbench 中選擇Mesh 模塊對實體模型進行網格劃分， 網格的結構和疏密程度將直接影響到計算結果的精度， 但是網格加密會增加計算機CPU 計算時間， 并需要更大的存儲空間。 理想的網格劃分， 是網格細化后， 求解結果不會發生明顯的改變。 Mesh 模塊會根據不同的物理場需求提供不同的網格劃分方法， 常見的網格劃分方法有： 自動網格劃分 （Automatic）、 四面體網格劃分 （Tetrahedrons）、 六面體主導網格劃分（Hex Dominant）、 掃掠法（Sweep）、 多區法（Multizone）、 膨脹法（Inflation） 等[4-5]。 為了綜合考慮計算精度與計算速度， 在劃分網格時， 采用程序自動網格劃分方法， 且網格單元尺寸設置為5 mm， 網格化的裝配體模型如圖2 所示， 其中網格單元數為17 703， 節點數為84 885。

圖2 網格化的齒輪裝配模型

2.4 邊界條件及載荷約束

由于主動輪和從動輪齒數較多， 每個嚙合齒面分別單獨進行接觸設置， 較為耗時。 為了快速準確地設置齒面接觸， 使用Named Selection 方法設置齒輪接觸。 齒輪嚙合屬于摩擦接觸， 摩擦系數設置為0.1。 由于齒輪嚙合時做旋轉運動，所以對嚙合的兩個齒輪分別添加運動副joint：body-ground， 類型選擇為轉動副Revolute， 使齒輪沿著軸線進行旋轉。 主動輪施加轉動速度Rotational Velocity， 大小設置為30 r/min； 從動輪施加一個阻尼力矩Moment， 大小設置為600 N·m，且方向與從動輪轉動方向相反。 在進行求解時，為了計算平穩， 打開大變形Large Deflection， 關閉弱彈簧Weak Springs。 為了確保一個完整的輪齒參與嚙合， 求解時間設置為0.2 s， 初始子步設為200， 最小子步設為20， 最大子步設為30 000。施加邊界條件及載荷約束如圖3 所示。

圖3 齒輪裝配模型邊界條件及載荷約束

2.5 計算結果及分析

通過對齒輪機構進行瞬態動力學分析， 得出齒輪嚙合過程中Von Mises 等效應力云圖、 最大等效應力局部放大圖、 齒面接觸狀態云圖、 齒面接觸應力云圖、 最大等效應變云圖， 如圖4所示。

從圖4 （a） 和圖4 （b） 可以看出， 最大等效應力出現在主動輪與從動輪剛接觸嚙合的位置上， 最大等效應力值為204 MPa。 齒輪材料的屈服強度σs為355 MPa， 齒輪在工作過程中不發生破壞的條件是其所受最大應力值σmax不超過許用應力[σ]， 即σmax≤[σ]。 而許用應力[σ] =σs/s，當安全系數s 取1.5 時， 得出 [σ] =237 MPa，即齒輪的許用應力為237 MPa， 可知齒輪所受的最大等效應力小于其許用應力， 滿足強度要求[6-8]。 從圖4 （e） 可知， 在齒輪嚙合傳動過程中， 最大等效應變同樣發生在主動輪與從動輪剛接觸嚙合的位置上， 最大等效應變僅為9.722 9×10-4mm，對齒輪影響較小。

圖4 （c） 齒面接觸狀態云圖中， 齒輪在嚙合過程中無粘結現象， 表明齒輪在嚙合傳動過程中齒面的接觸狀態良好[9-10]。 圖4 （d） 的齒面接觸應力云圖中， 最大接觸應力出現在靠近節線的齒根面附近， 最大接觸應力值為60.83 MPa，遠小于齒輪的許用應力。 齒輪齒面最為常見的失效形式是點蝕， 其產生的原因是齒面在變化的接觸應力作用下， 由于疲勞而產生麻點狀損傷現象。 點蝕最先出現在靠近節線的齒根面上，然后再向其他部位擴展[11]， 點蝕最先出現的位置與本次分析的齒面最大接觸應力部位相同， 表明此次研究分析合理有效。

圖4 齒輪機構瞬態動力學分析結果

通過對齒輪嚙合過程中， 最大等效應力值隨時間變化的數據進行統計后， 得出最大等效應力隨時間變化曲線如圖5 所示。 從圖5 可以得出， 主動輪與從動輪剛接觸嚙合的時候， 所產生的等效應力最大， 應力值波動范圍較大，最大值為204 MPa。 但隨著時間的推移， 應力值趨向于穩定， 這是因為在開始嚙合轉動過程中， 由于主動輪具有一定的沖擊力， 導致齒輪嚙合產生的等效應力值較大， 但隨著嚙合的穩定進行， 齒輪嚙合等效應力趨向于穩定。

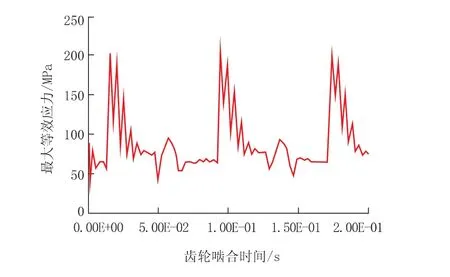
圖5 最大等效應力隨時間變化曲線

3 結 論

（1） 在等效應力云圖中， 最大等效應力出現在主動輪與從動輪剛接觸嚙合位置上， 最大等效應力值為204 MPa， 小于許用應力值， 滿足強度使用要求。 在等效應變云圖中， 最大應變值僅為9.722 9×10-4mm， 對齒輪影響較小。

（2） 在接觸應力云圖中， 最大接觸應力值為60.83 MPa， 出現在靠近節線的齒根面附近，與齒輪通常最先出現點蝕位置相同。 在接觸狀態云圖中， 齒輪嚙合過程中無粘結現象， 表明齒面接觸狀態良好。

（3） 在最大等效應力隨時間變化曲線中， 齒輪開始嚙合時， 所受最大等效應力值較大， 但隨著齒輪嚙合的穩定運行， 齒輪嚙合等效應力趨向穩定。