導數在高考中的應用分析
◇ 山東 劉士臣
導數是高考數學的必考內容,是解決相關問題的重要工具,在歷年高考中,導數常與方程、函數及不等式等知識點交會進行考查,往往一個高考題涉及多個方面的知識.下面我們通過分析高考題來分析導數的具體應用.
例1已知函數f(x)=2x3-ax2+2.
(1)討論f(x)的單調性;
(2)當0<a<3時,記f(x)在區間[0,1]的最大值為M,最小值為m,求M-m的取值范圍.
解析
本題考查了學生的運算求解能力、推理論證能力以及分類討論思想的應用.
(1)易知f′(x)=6x2-2ax=2x(3x-a).令f′(x)=0,得x=0或,若a>0,則當x∈時,f′(x)>0;當時,f′(x)<0,故f(x)在上單調遞增,在上單調遞減.若a=0,f(x)在(-∞,+∞)上單調遞增.若a<0,則當+∞)時,f′(x)>0;當時,f′(x)<0,故f(x)在上單調遞增,在上單調遞減.
(2)當0<a<3時,由(1)知,f(x)在上單調遞減,在上單調遞增,故f(x)在[0,1]的最小值為,最大值為f(0)=2或f(1)=4-a.于是所以
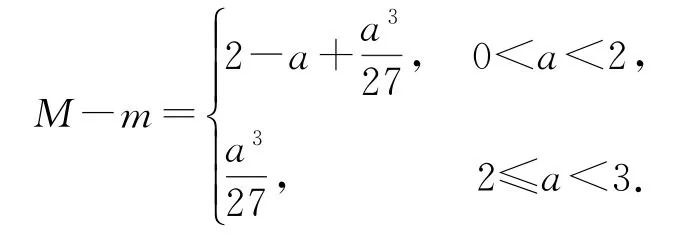
當0<a<2時,可知單調遞減,所以M-m的取值范圍是.當2≤a<3時,y=單調遞增,所以M-m的取值范圍是
綜上,M-m的取值范圍是
點評
含參數函數單調性的討論,關鍵在于確定參數的分界值.解題時易犯以下兩個錯誤:①對參數a未討論或對a分類不全面,易忽略a=0的情形而導致失分;②當a>0時,f(x)在(-∞,0),單調遞增,中間應該用“,”或“和”連接,寫成就會導致失分.
例2已知函數f(x)=2 sinx-xcosx-x,f′(x)為f(x)的導數.
(1)證明:f′(x)在區間(0,π)存在唯一零點;
(2)若x∈[0,π]時,f(x)≥ax,求a的取值范圍.
解析
本題考查了學生的推理論證、運算求解能力以及靈活運用數形結合思想去分析和解決問題的能力.
(1)設g(x)=f′(x),則
g(x)=cosx+xsinx-1,g′(x)=xcosx.
(2)由題設知f(π)≥aπ,f(π)=0,故可得a≤0.由(1)知,f′(x)在(0,π)只有一個零點,設為x0,且當x∈(0,x0)時,f′(x)>0;當x∈(x0,π)時,f′(x)<0,所以f(x)在(0,x0)上單調遞增,在(x0,π)上單調遞減.
又因為f(0)=0,f(π)=0,故當x∈[0,π]時,f(x)≥0.當a≤0,x∈[0,π]時,ax≤0,故f(π)≥aπ.因此,a的取值范圍是(-∞,0].
點評
本題第(2)問充分利用了第(1)問的結論,使問題大大簡化了.

