空間立體幾何中的外接球問題

◇ 新疆 蘇倫高娃

球是一種重要幾何體,由于球自身的完美對稱性,常常與一些簡單幾何體(如柱、錐、臺)結合,求外接球的表面積、體積,這是高考考查的重點和難點．這一類問題,學生的得分率較低,大部分學生都不知道如何下手,歸根結底在于學生對空間問題的想象能力、推理能力和計算能力都有所欠缺．對此本文來談談筆者是如何在教學過程中引導學生解決此類問題的．

預備知識：

1)球心和截面圓心的連線垂直于截面；

2)球心到截面的距離d與球的半徑R及截面的半徑r滿足：R2＝d2＋r2；

3)圓的直徑所對的圓周角為直角．

1 正方體或長方體的外接球

例1 已知各頂點都在同一個球面上的長方體的三條棱長分別為1,2,3,則此球的表面積為_______．

解析

要求球的表面積,只需求出長方體外接球的半徑,所以應先確定球心的位置,求出球的半徑．

因為外接球球心就是長方體體對角線的中點,半徑是長方體體對角線長的一半,即,求得外接球的半徑后,代入球的表面積公式S＝4 πR2,可得球的表面積為14 π．

問題：在上題中,以長方體中任意不共面的四個頂點為頂點,可以構成什么樣的幾何體?有哪幾種?它們的外接球是怎樣的?

筆者在這個環節中提前準備了學案,給學生充分的時間去構造空間四面體(如圖1)．

通過直觀感受和交流討論,學生能夠順利推出四面體的外接球和長方體的外接球是同一個球,從而四面體的外接球問題可轉化為長方體的外接球問題進行求解．

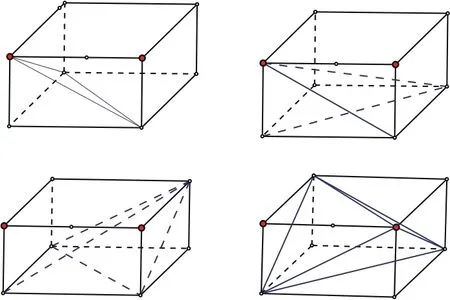
圖1

例2《九章算術》中,將底面為長方形且由一條側棱與底面垂直的四棱錐稱之為陽馬；將四個面都為直角三角形的三棱錐稱之為鱉臑．若三棱錐P-ABC為鱉臑,PA⊥平面ABC,PA＝AB＝2,AC＝4,三棱錐P-ABC的四個頂點都在球O的球面上,則球O的表面積為________．

解析

本題的求解思想就是將三棱錐P-ABC放入長方體中,如圖2,三棱錐的外接球就是長方體的外接球．因為PA＝AB＝2,AC＝4,△ABC為直角三角形,所以．設外接球的半徑為R,由題意得,故球的表面積為20 π．

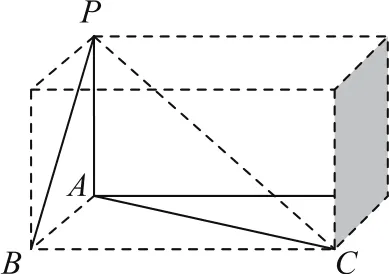
圖2

特別地,當長方體為正方體時,還可以利用正方體的性質求解外接球問題．

例3已知三棱錐P-ABC中,PA,PB,PC兩兩垂直,且長度相等．若點P,A,B,C都在半徑為1的球面上,則球心到平面ABC的距離為________．

解析

如圖3,因為PA,PB,PC兩兩垂直,故正三棱錐P-ABC的外接球就是以PA,PB,PC為棱的正方體的外接球．球心在正方體體對角線的中點上,根據正方體的性質,平面PBC具有很多良好的性質,如體對角線PD⊥平面ABC,垂足是PD的一個三等分點,所以球心到平面ABC的距離為半徑的

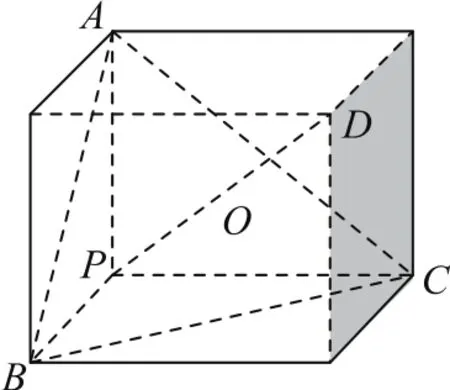
圖3

2 求與棱柱外接球有關的計算問題

例4設正三棱柱的側棱垂直于底面,所有棱長都為a,頂點都在一個球面上,則該球的表面積為_______．

解析

如圖4所示,P為三棱柱底面中心,O為球心,易知則球的半徑滿足R2＝AO2＝AP2＋,所以,球的表面積為

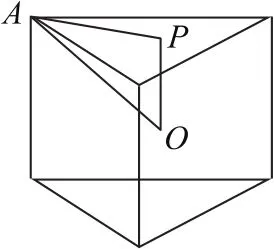
圖4

3 求與棱錐外接球有關的計算問題

例5已知球O是三棱錐S-ABC的外接球,△ABC是邊長為1的等邊三角形,SC是球O的一條直徑,SC＝2,則三棱錐S-ABC的體積為________．

解析

因為三棱錐S-ABC和三棱錐O-ABC有共同的底面ABC,球心O為SC的中點,所以三棱錐S-ABC的高為三棱錐O-ABC高的2倍,即VS-A B C＝2VO-A B C．

如圖5所示,三棱錐O-ABC的棱長都是1,取等邊△ABC的中心D,點D即為底面ABC外接圓(即截面圓)的圓心,球心O在點D的正上方,則OD⊥平面ABC．因為截面圓半徑,因為球的半徑R＝OC＝1,則

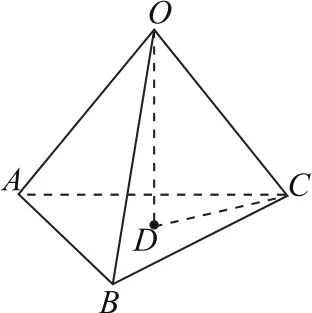
圖5

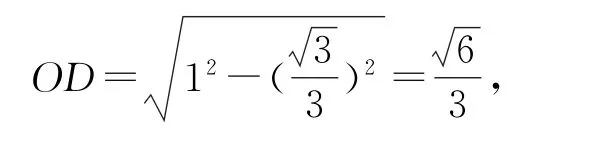
所以

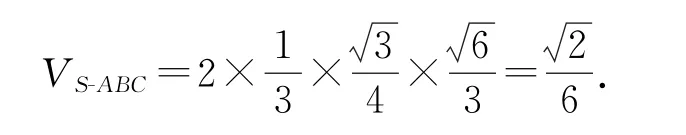
從近幾年的高考試題來看,經常出現與外接球有關的問題,本文結合筆者在教學過程中的做法,推廣出與外接球有關問題的具體解法,以便學生比較容易地掌握球的性質及與外接球有關的計算問題．