圓錐曲線問題融入“心”中

◇ 重慶 何朝樞

三角形的“四心”(垂心、重心、內心、外心)具有各自不同的幾何定義與性質,而在圓錐曲線問題中巧妙融合入三角形的“心”,是一類既富交會性、思考性和挑戰性,又具有一定難度和深度的數學問題,在近年的高考中時常出現,是考查學生的思維方式和數學能力的一個好方式．

1 圓錐曲線問題融入“垂心”

例1在平面直角坐標系x Oy中,已知橢圓C：的焦距為2,且過點

(1)求橢圓C的標準方程；

(2)設橢圓C的上頂點為B,右焦點為F,直線l與橢圓交于M,N兩點,問是否存在直線l,使得F為△BMN的垂心．若存在,求出直線l的方程；若不存在,說明理由．

解析(1)由題目條件可得a2＝b2＋c2,解得a2＝2,b2＝1,所以橢圓C的標準方程為

(2)假設存在直線l滿足題設條件,即直線l與橢圓交于M,N兩點,且F為△BMN的垂心．

如圖1所示,由(1)可得B(0,1),F(1,0),則有,由于點F為△BMN的垂心,則有BF⊥直線l,可得kl＝,可設直線l的方程為y＝x＋m,設M(x1,y1),N(x2,y2),聯立消去參數y并整理可得3x2＋4mx＋2m2－2＝0．

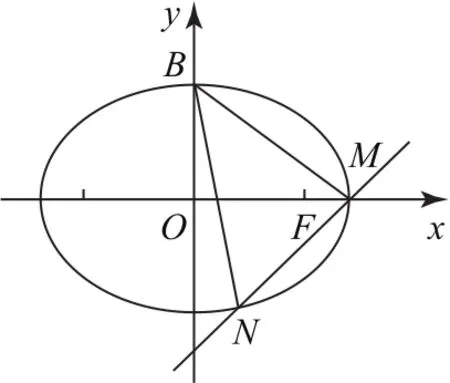
圖1

2 圓錐曲線問題融入“重心”

例2已知點A,B,C為橢圓上三個不同的點,O為坐標原點,若2則△ABC的面積為( )．

解析

當直線AB的斜率存在時,可設直線AB的方程為y＝kx＋m,設A(x1,y1),B(x2,y2),代入橢圓方程x2＋2y2＝2,消去y并整理可得(1＋2k2)x2＋4kmx＋2(m2－1)＝0．根據根與系數的關系,可得

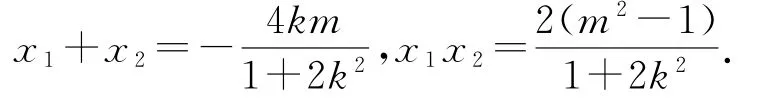
設C(x3,y3),由于,可得x3＝,將點C(x,y)代入橢圓方程33x2＋2y2＝2,整理可得1＋2k2＝4m2,而根據弦長公式有到直線AB的距離,則有結合三角形的重心的幾何意義與性質,可得S△A B C＝；根據選擇題的唯一性,當直線AB的斜率不存在時不加以具體分析,此時也可得．故選C．

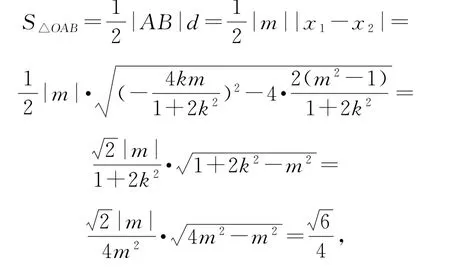
3 圓錐曲線問題融入“內心”

例3已知F1,F2分別為橢圓(a＞b＞0)的左、右焦點,求橢圓C的離心率e為,點P是橢圓C上除長軸頂點外的任意一點,而△PF1F2的內切圓的圓心為I,設直線IF1,IF2的斜率分別為k1,k2,則k1k2＝________．

解析

設△PF1F2的內切圓的圓心I在三角形的對應三邊上的投影分別為D,E,H,根據三角形的內心的幾何意義與性質,設|F1D|＝|F1H|＝m,|F2D|＝|F2E|＝n,|PE|＝|PH|＝p,內切圓的半徑為r,如圖2所示．

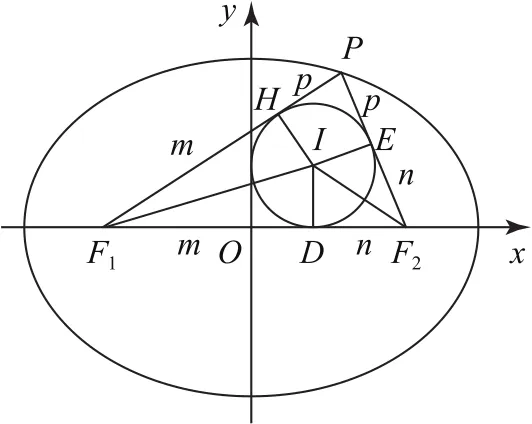
圖2

利用橢圓的定義,可得|PF1|＋|PF2|＝m＋n＋2p＝2a,又|F1F2|＝m＋n＝2c,則有p＝a－c,結合海倫公式可得△PF1F2的面積為S＝,結合三角形的內切圓的性質可得△PF1F2的面積為S＝(m＋n＋p)r,那么

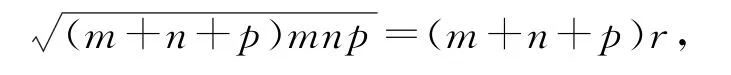
整理有mnp＝(m＋n＋p)r2,結合圖形直觀,可得

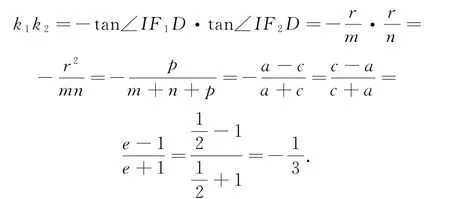
同時要注意對應問題中三角形的“心”的表達方式與“心”的名稱,正確區分各“心”的性質及其結構特征,再結合圓錐曲線的相關知識加以合理應用．合理融入“心”,增加問題的交會性,讓學生真正領悟到數學的和諧之美．