矮塔斜拉橋地震損傷試驗研究

王獻摯，鄧治國，李建中

(1. 同濟大學 土木工程防災國家重點實驗室，上海 200092；2. 山西路橋集團運寶黃河大橋建設管理有限公司，太原 030006)

近年來，矮塔斜拉橋作為一種介于連續梁(剛構)橋和斜拉橋之間的組合體系橋型，以其良好的結構性能和經濟指標，在國內外取得迅猛發展[1-2]。據相關統計[3]，截至2012年，在全世界范圍內已有近百座矮塔斜拉橋建成，其中有50余座在我國境內。而國內外歷次大地震的教訓表明，在強震作用下，橋梁作為交通運輸工程中的樞紐環節，一旦遭到嚴重損傷，會對救災工作造成巨大困難。因此，基于矮塔斜拉橋的廣闊應用前景，其抗震性能已逐漸引起國內外學者的關注。

目前，針對矮塔斜拉橋抗震性能的研究大多集中在地震響應數值計算上，如：蔡鵬程[4]以福建漳州戰備大橋主橋為背景，采用ANSYS建立模型，選取支承條件、邊主跨比、主梁高跨比和主塔高跨比4個參數進行地震反應分析；朱保華[5]采用Midas/Civil建立了一座多塔矮塔斜拉橋的有限元模型，分析了索塔形式和跨數對多塔矮塔斜拉橋動力特性的影響；谷音等[6]基于OpenSees建立了典型矮塔斜拉橋的非線性模型，采用增量動力分析法(Incremental Dynamic Analysis，IDA)進行非線性時程分析，分別探討了在縱橋向和橫橋向地震作用下矮塔斜拉橋結構的構件破壞規律；陳卓[7]采用SAP2000對四方橋進行動力特性研究，并選用一系列鉛芯橡膠支座進行減隔震研究；劉昊蘇等[8]基于Midas/Civil建立曲線矮塔斜拉橋模型，研究不同的橋梁設計半徑及墩梁的連接形式對橋梁抗震性能的影響。

此外，在模型試驗方面，彭晶蓉[9]通過對某部分斜拉橋進行縮尺，開展了靜力相似試驗，模擬實橋施工過程和成橋運營階段的結構響應；Yang等[10]以南昌朝陽大橋為背景，設計了半結構振動臺模型試驗，比較了拉索支座體系與摩擦支座體系下結構關鍵位置的響應。

綜上所述，國內外學者對矮塔斜拉橋開展的研究已取得初步成果，但主要依托于有限元數值模型分析，在試驗方面的研究仍較少，并且尚未對矮塔斜拉橋的地震損傷過程進行過研究。而振動臺試驗作為一種直接模擬地震激勵、觀測結構動力響應的試驗方法，能夠真實反映結構動力特性，檢驗結構抗震性能，研究結構地震損傷發展過程。因此，很有必要開展針對矮塔斜拉橋地震損傷過程的振動臺試驗研究。

本文基于同濟大學土木工程防災國家重點實驗室的多功能振動臺試驗室，以一座典型多塔矮塔斜拉橋為研究對象，設計了縮尺比為1/20的全橋振動臺試驗模型，進行了振動臺模型縱橋向破壞性試驗，研究矮塔斜拉橋在強震作用下的損傷發展過程，為將來矮塔斜拉橋的抗震分析和設計理論研究提供最直接的試驗數據。

1 試驗模型設計

1.1 背景工程

本文選取某典型塔墩梁固結體系矮塔斜拉橋為工程背景，該橋是一座跨徑布置為110 m+200 m+200 m+110 m的三塔矮塔斜拉橋，全長620 m，如圖1所示。圖1中，主梁為單箱五室變截面箱型梁，頂板寬34 m，底板寬25 m，根部梁高7 m，跨中梁高3 m；三個主塔均為人字形，塔高33 m，塔身橫向寬2.9 m，縱向上部塔身寬7 m，下部分作兩斜腿，底部總寬9 m；每個主塔上各設26對斜拉索，采用單索面雙排索的布置形式，每排13對，兩排橫向間距1 m；下部結構三處主墩均采用雙薄壁實體墩，墩高分別為40 m，45 m和45 m，兩處連接墩均采用等截面空心墩；連接墩上設雙向活動支座。

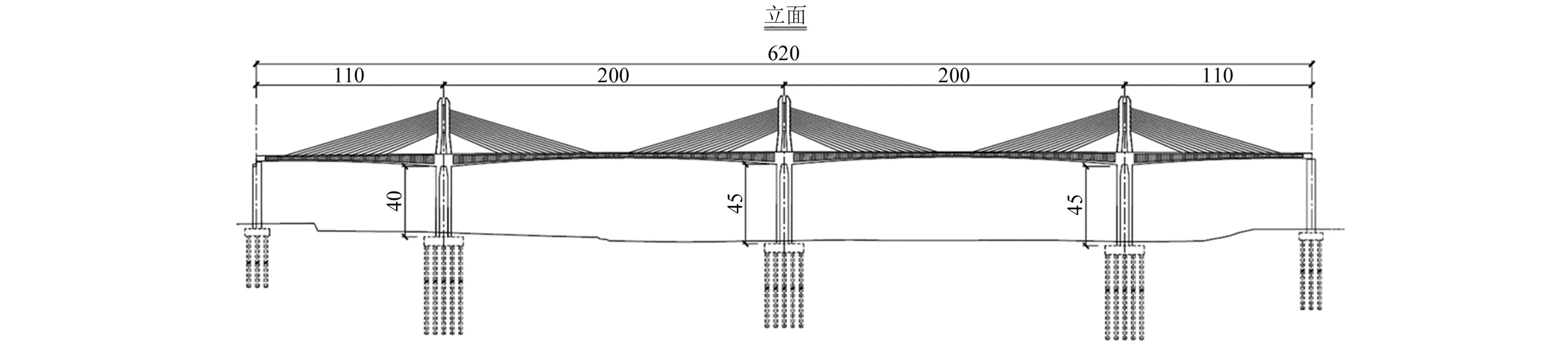
圖1 典型矮塔斜拉橋總體布置圖(m)Fig.1 Schematic of typical extra-dosed cable-stayed bridge (m)

1.2 振動臺試驗模型設計

1.2.1 相似常數設計

振動臺試驗模型的設計需要綜合考慮振動臺承載能力及試驗場地尺寸等因素。本試驗根據同濟大學多功能振動臺試驗室的場地與試驗設備條件，確定試驗模型縮尺比為1∶20。而為了方便試驗模型的制作與安裝，試驗模型的主梁按照剛度等效與質量等效的原則簡化為鋼梁，采用冷軋Q345qD鋼板制作。試驗模型的主塔、主墩等構件均采用M15微粒混凝土，混凝土的彈性模量相似常數取為1/3。由于試驗模型與原型在同一重力場中，為免重力模擬失真，加速度相似常數取為1。其余物理量的相似常數采用量綱分析法分別進行推導，如表1所示。

表1 試驗模型相似常數

依據上述相似常數進行模型總體設計，得到試驗模型總長為31 m，模型振動臺布置如圖2所示。本試驗中每處主塔與其對應的主墩采用整體澆筑方式制作，合稱作橋塔，分別記為T1，T2及T3。模型主梁為鋼梁，通過梁端與橋塔預埋件焊接來實現塔梁墩固結。三個橋塔T1，T2及T3分別安裝在振動臺C臺、B臺與D臺上，兩側連接墩分別安裝在試驗槽道兩側的地面上。

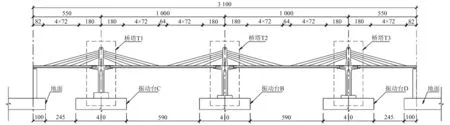
圖2 試驗模型振動臺布置圖 (cm)Fig.2 Shaking table layout of test model (cm)

1.2.2 橋塔設計

試驗模型橋塔尺寸嚴格遵循相似比進行設計。而橋塔截面配筋設計時，若仍遵循1∶20的縮尺比，將出現鋼筋直徑過小的問題，給模型制作帶來巨大困難。因此本試驗主要把握構件層面的抗彎能力等效與抗剪能力等效原則[11]，分別對試驗模型橋塔各截面進行配筋設計，使試驗模型與原型剛度相似，能夠反映原型的地震響應特點及損傷破壞過程。以T2橋塔為例，其構造及截面配筋如圖3所示。

圖3 試驗模型橋塔設計圖(cm)Fig.3 Design of main tower of test model (cm)

1.2.3 主梁設計

大量研究表明，地震作用下，矮塔斜拉橋的地震易損部位主要是主塔與主墩，主梁所受地震力普遍較小，一般在彈性范圍內工作。因此在試驗模型主梁設計時，主要按照剛度等效和質量等效原則，把原型混凝土梁等效設計為鋼梁。

鋼梁截面首先依據原型主梁截面尺寸進行初步擬定，而后按照剛度等效原則，通過逐步調整及試算，使全橋自振周期基本與原型接近，從而得到等效主梁截面，如圖4所示。最后，按照質量等效原則，計算出與原型混凝土梁質量相似的鋼梁質量。

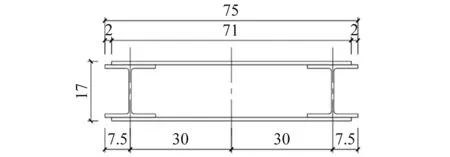
圖4 試驗模型主梁設計圖(cm)Fig.4 Design of main girder of test model (cm)

1.2.4 斜拉索設計

由于原型斜拉索錨點間距較小，縮尺后無法滿足斜拉索端部錨點構造要求，因此按照斜拉索總體豎向分力等效的原則，將每個主塔上的26對斜拉索縮減作5對，梁上錨點間距取0.72 m，塔上錨點間距取0.15 m。此外，模型斜拉索采用直徑12.5 mm鋼絲繩，以滿足試驗中最大索力需求。

1.2.5 配重與支承設計

對于振動臺試驗，為準確反映原型結構抗震性能，需要確保試驗模型慣性力與原型相似，即確保結構質量相似[12]。由于模型材料密度有限，僅靠模型自身質量，無法滿足結構質量相似要求。因此，需要根據按質量相似常數計算得到的試驗模型理論質量對模型進行配重設計。

本試驗中模型主要構件的附加質量如表2所示。配重布置如圖5所示。其中，主梁配重采用方形配重鋼塊的形式施加，單塊質量為2 t；橋塔配重則采用配重箱的形式施加，對稱布置，箱中放置鑄鐵塊與鉛塊，并嵌入楔子以使鑄鐵塊與鉛塊緊實。

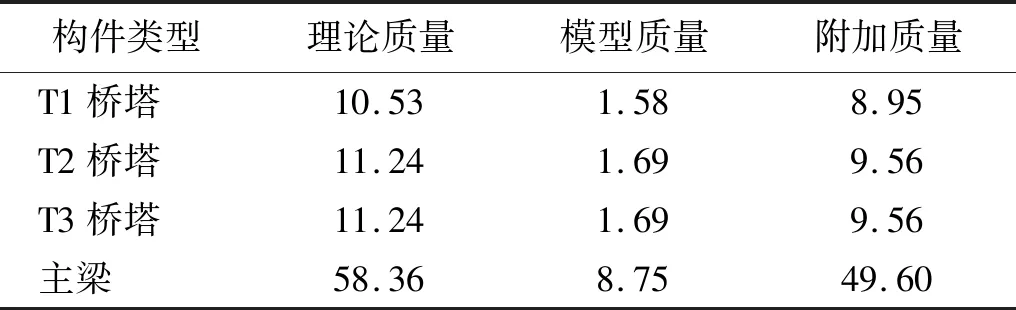
表2 試驗模型配重設計

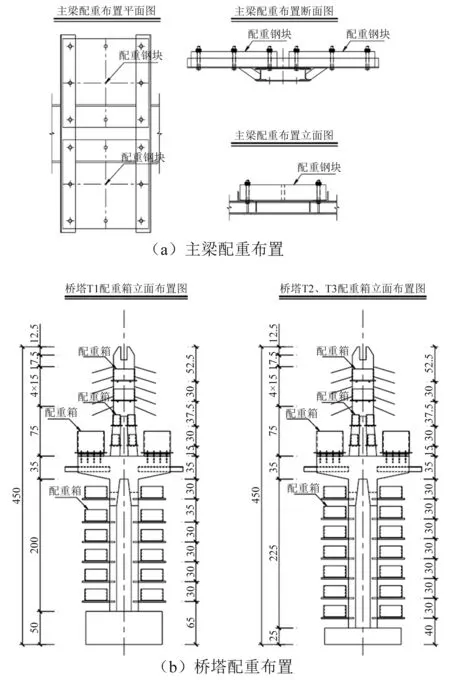
圖5 試驗模型配重布置圖Fig.5 Elevation of additional mass of test model

此外，本試驗兩個連接墩處采用雙向滑動的四氟滑板橡膠支座來模擬原橋的雙向活動支座。

按照上述設計方法制作、安裝完成后的振動臺試驗全橋模型如圖6所示。

圖6 振動臺全橋試驗模型Fig.6 Completed test model on shaking tables

1.3 有限元驗證

在模型設計過程中，由于難以制造出嚴格遵循各項相似關系的理想模型，本試驗進行了部分簡化處理(主要是橋塔截面配筋設計、主梁截面等效設計及斜拉索并索處理)得到試驗模型。為驗證上述簡化過程的合理性，本節采用SAP2000軟件建立了有限元模型，對比理想模型和試驗模型的模態分析和反應譜分析結果。其中，反應譜分析時輸入的是原型橋梁場址處地震安全性評價報告提供的相應于E2概率水平(罕遇地震)的場地加速度反應譜，如圖7所示。

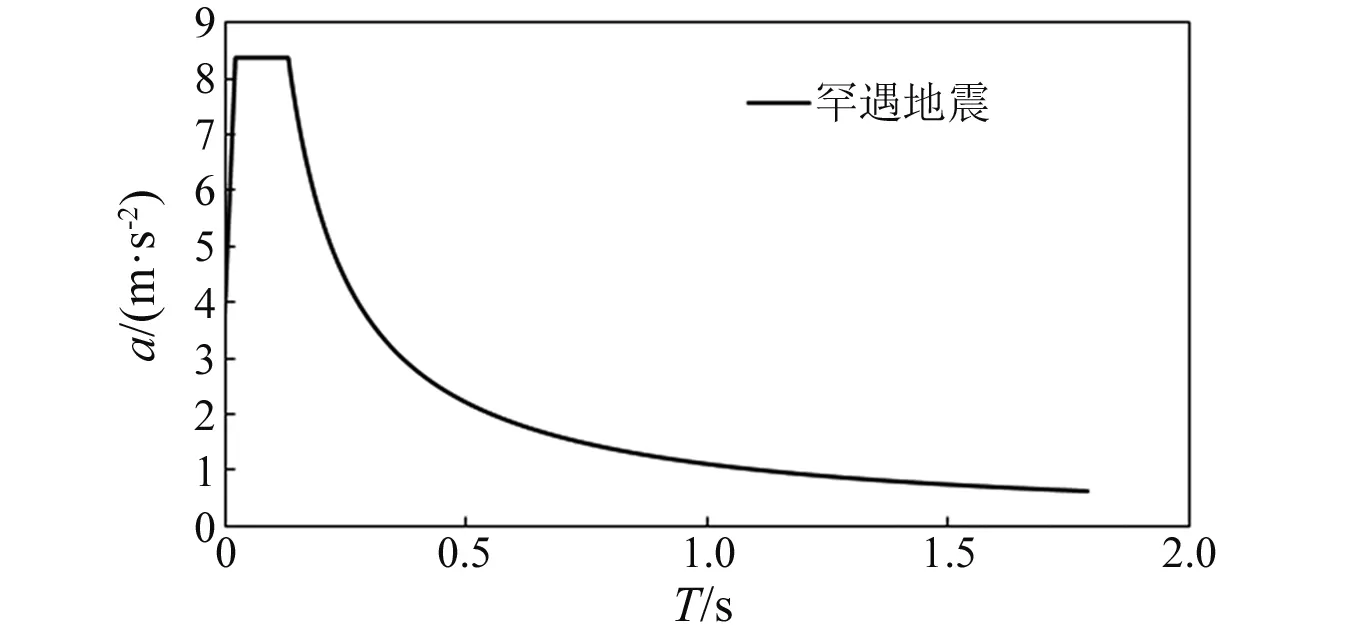
圖7 E2反應譜Fig.7 E2 response spectrum

采用SAP2000軟件建立的理想模型有限元模型如圖8所示。理想模型的結構尺寸、材料彈性模量與密度等均嚴格遵循其與原型橋梁的相似關系。主梁、主塔與主墩均采用彈性梁單元模擬，單元材料為M15微粒混凝土，彈性模量按1/3的相似常數取為1.183×104MPa，主梁二期恒載以線質量形式實現；斜拉索采用桁架單元模擬，每個主塔各26對拉索，單根拉索截面直徑為4.935×10-3m；連接墩與主梁間的活動支座采用縱、橫向活動的線性連接單元模擬。

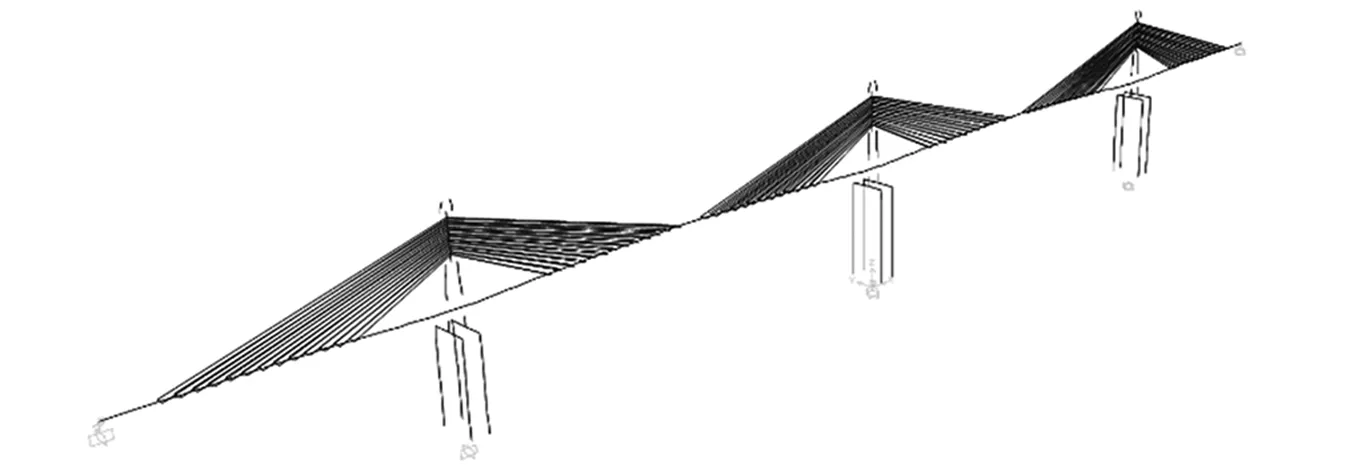
圖8 理論模型有限元模型Fig.8 The finite element model of theoretical model

試驗模型有限元模型的主塔、主墩尺寸與理想模型有限元模型一致，主梁則采用1.2.3節所設計的鋼梁截面，單元材料為Q345qD鋼材，彈性模量按1.0的相似常數取為2.1×105MPa，附加質量按1.2.5節設計。每個主塔各5對拉索，單根拉索截面直徑為12.5 mm。連接墩處的四氟滑板橡膠支座采用縱、橫向活動的線性連接單元模擬。

理想模型與試驗模型的縱橋向一階自振周期和主墩墩底縱向彎矩反應譜分析結果的對比如表3所示。由表中結果可知，簡化后的試驗模型能夠較為準確地反映出原型結構的動力特征和地震響應，可以用來進行振動臺試驗。

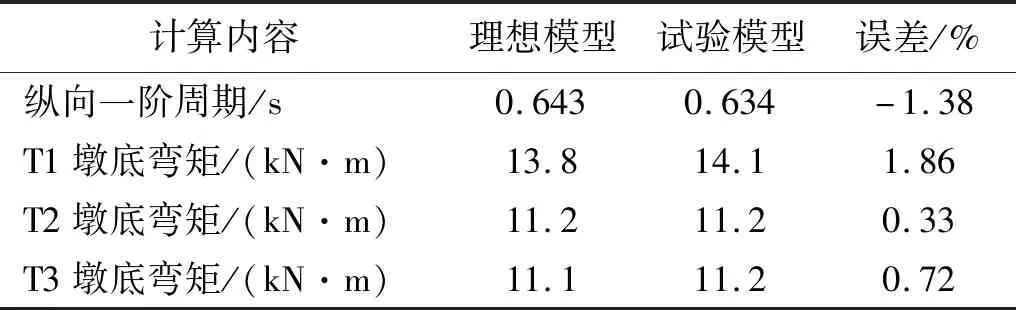
表3 理論模型與試驗模型分析結果對比

2 試驗工況與測點布置

2.1 地震波選取

本試驗選取一條與原型橋梁場地類型相同的實際地震記錄(El Centro波)和一條人工合成地震波(場地人工波)作為振動臺臺面輸入。其中，El Centro波是1940年美國加州埃爾森特羅地震中在El Centro Array #9站臺記錄的[13]，加速度峰值0.280 8g，持續時間53.71 s；而場地人工波依據圖7所示E2反應譜人工擬合的地震動加速度記錄，加速度峰值0.385 1g，持續時間40 s。

將上述地震動分別調整到加速度峰值為0.1g，并按照時間相似常數St=0.223 6進行時間軸壓縮，通過峰值歸一化與時間軸壓縮處理后得到的加速度時程曲線，如圖9所示。

2.2 工況設計

為研究矮塔斜拉橋的抗震性能與地震損傷發展過程，本試驗主要設計了兩個工況。A工況采用El Centro波加載，控制結構在彈性范圍；B工況采用場地人工波加載，通過逐級增大場地人工波的峰值地面加速度(Peak Ground Acceleration, PGA)[14]，對該試驗模型進行地震損傷試驗，一直加載至結構破壞。

試驗時，按照表4所示的各試驗工況峰值加速度，將圖9所示調整后的El Centro波和場地人工波加速度時程曲線分別乘以相應的放大倍數，在三個振動臺沿縱橋向進行一致輸入。

表4 試驗加載工況

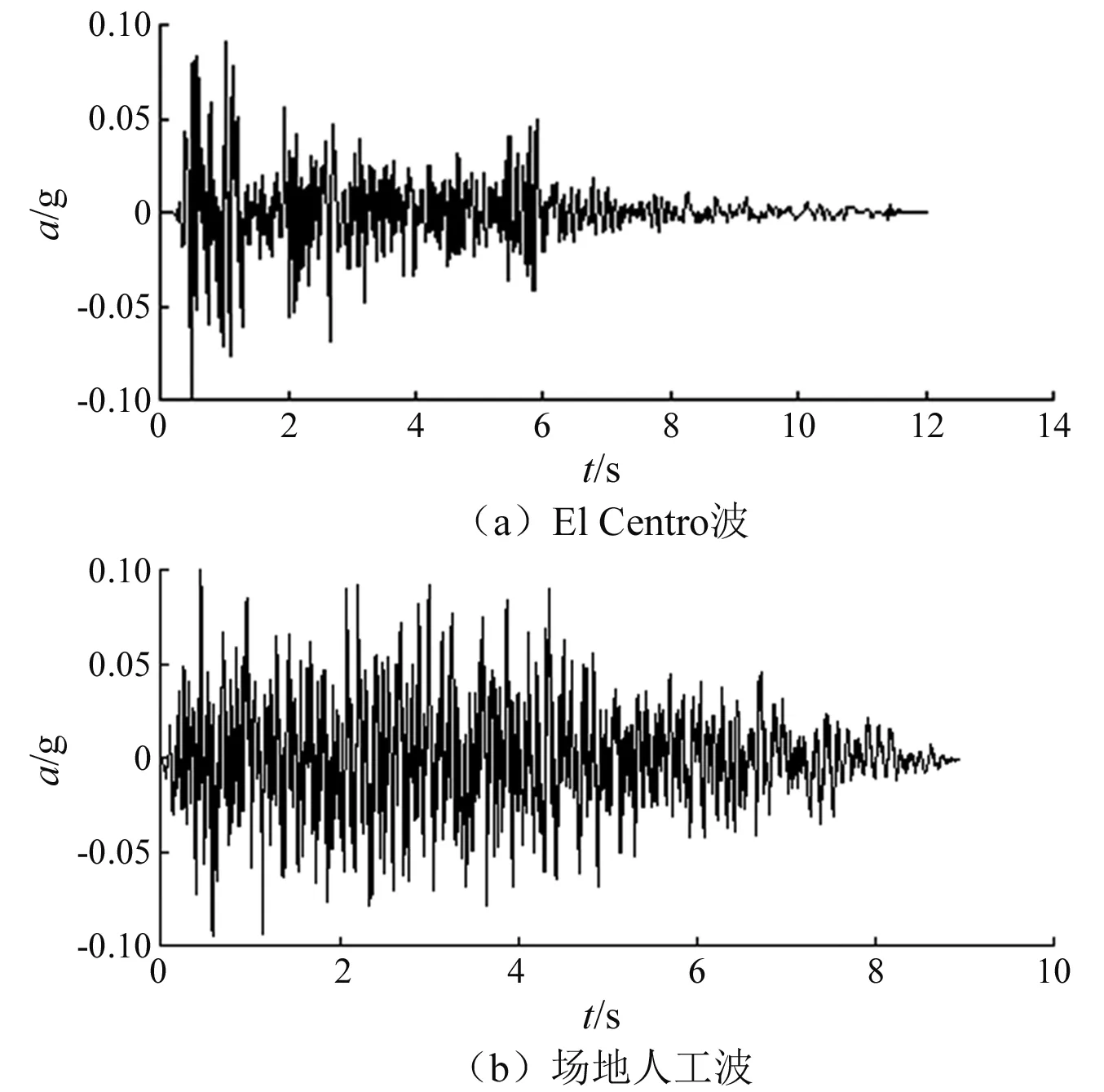
圖9 振動臺試驗輸入地震波Fig.9 Earthquake wave of shaking table tests

各工況開始前，均采用白噪聲對試驗模型進行掃頻試驗，測量結構自振頻率等動力特征參數，記錄結構破壞過程中的動力特征變化。

2.3 測點布置

為了測量試驗過程中結構地震響應，本試驗共用242個數據采集通道。其中，加速度計18個，位移計18個，力傳感器30個，應變片176個，具體分布情況如表5所示。

表5 試驗測點布置

3 試驗結果分析

3.1 試驗現象描述

通過在每個工況結束后觀察試驗模型的損傷情況，記錄得到如下試驗現象：

在加載工況A中，振動臺臺面輸入PGA相對較小(0.10～0.30g)，主橋縱向振動幅度較小，主塔與主墩表面均沒有出現裂縫。

在加載工況B中，在振動臺臺面輸入PGA較小時(0.10～0.30g)，主橋縱向振動幅度較小，主塔與主墩表面均沒有出現裂縫；當振動臺臺面輸入PGA達到0.35g時，橋塔T1，T3的主墩墩底處混凝土開始出現微裂縫，裂縫寬度均小于0.1 mm；當臺面輸入PGA在0.40～0.60g時，主墩墩底部位和墩頂部位陸續出現新裂縫，且舊裂縫進一步延展，部分形成了貫穿截面的環狀裂縫；當臺面輸入PGA在0.70～0.90g時，主墩墩底部位和墩頂部位出現了局部混凝土輕微剝落的現象；當臺面輸入PGA在1.00g時，主墩墩底部位和墩頂部位混凝土的剝落情況加劇，出現小面積剝落，暴露出部分縱筋與箍筋；當臺面輸入PGA在1.10～1.20g時，主墩墩底部位和墩頂部位的混凝土剝落面積進一步增大，其中墩底部位局部有大塊混凝土剝落，縱筋與箍筋更明顯地露出，個別縱筋發生輕微的屈曲變形；當臺面輸入PGA在1.30～1.50g時，主墩墩底部位和墩頂部位混凝土發生大面積剝落，出現屈曲變形的縱筋增多，墩底部位的部分核心混凝土碎裂，并逐漸與縱筋箍筋剝離，剝離處箍筋鼓起，縱筋屈曲變形嚴重。至此，橋塔發生嚴重破壞。此時，主塔無明顯裂縫，主橋有一定殘余位移，但并未倒塌，為安全考慮，停止試驗加載。試驗停止后，結構損傷情況(以T2橋塔為例)如圖10所示。

圖10 試驗模型損傷情況Fig.10 Damage situation of test model

由圖10可知：①由于縱橋向雙薄壁墩形式主墩及塔梁墩固結體系主橋的框架效應，試驗模型地震損傷主要出現在主墩墩底與墩頂部位，主塔基本無損傷；②主墩墩底部位損傷嚴重，混凝土壓潰，箍筋鼓出，縱筋嚴重屈曲；③隨著主墩墩底部位形成塑性鉸，框架效應減弱，因此主墩墩頂部位的損傷情況沒有主墩墩底部位嚴重，僅表現為保護層混凝土剝落和縱筋輕微屈曲。

3.2 動力特性

本試驗在加載工況A開始前，采用峰值加速度為0.10g的白噪聲對試驗模型進行了掃頻試驗，以三個橋塔塔頂觀測點的加速度響應對相應臺面輸入的白噪聲信號做傳遞函數，得到傳遞函數的幅頻圖如圖11所示。由圖11可知，三個橋塔塔頂加速度幅頻曲線基本吻合，一階自振頻率可明顯識別，為1.375 Hz，即一階周期0.727 s。再通過半功率帶寬法，計算得到試驗模型一階振型阻尼比為0.081。

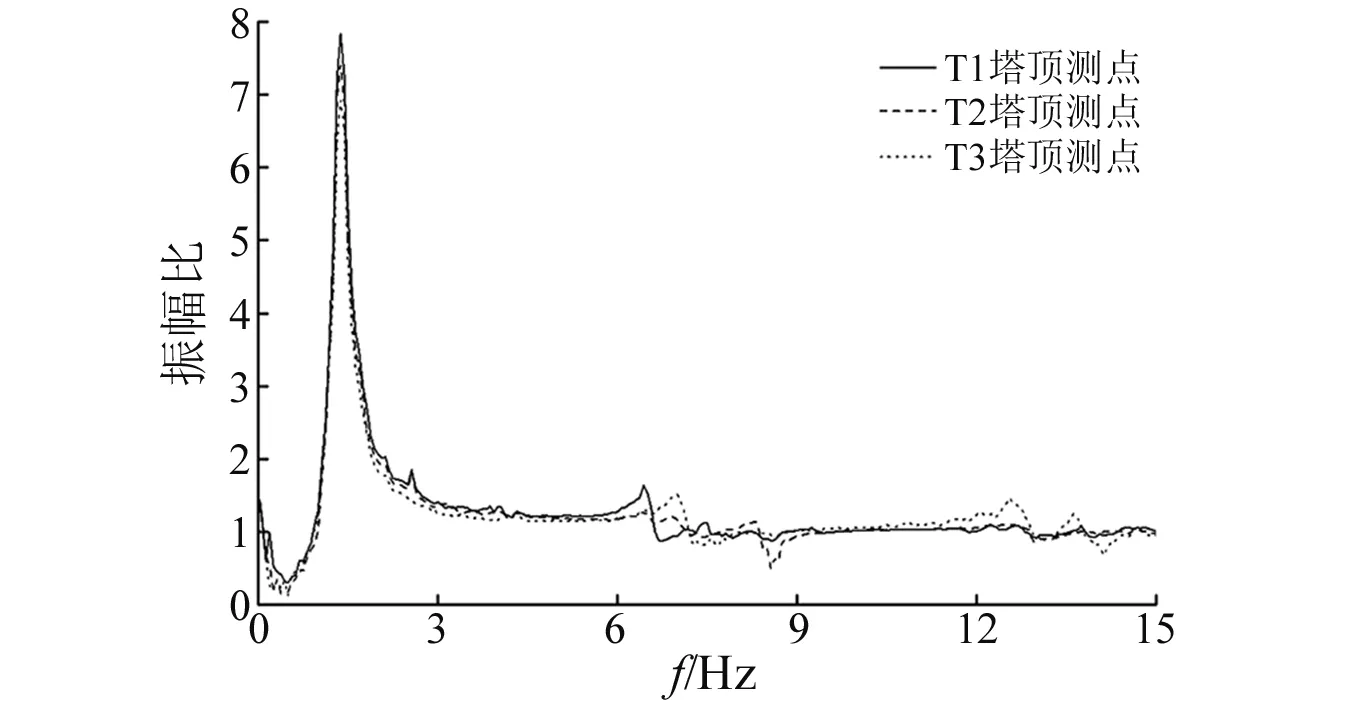
圖11 白噪聲激勵下的塔頂加速度測點傳遞函數幅頻圖Fig.11 Amplitude-frequency diagram

由表3可知，試驗模型一階周期目標值為0.634 s，而實測一階周期為0.727 s，存在一定誤差，但總體而言試驗模型的動力特征參數與設計預期基本相符，能夠反映原型地震響應特點。

另外，以T2橋塔為例，將沿橋塔高度方向布置的三個縱橋向加速度測點(主墩中部、主墩墩頂及主塔塔頂處)的傳遞函數幅頻特性，經歸一化后得到該白噪聲工況下橋塔縱橋向一階振型示意圖如圖12所示。由圖12可知，本試驗中矮塔斜拉橋的一階振型表現為橋塔縱橋向振動。不同于常規斜拉橋橋塔的是，矮塔斜拉橋一階振型的主塔塔頂處與主墩墩頂(即主塔塔底)處的振幅很接近，說明主塔自身振動幅度較小，全橋縱向振動基本為主墩振動，這也印證了試驗中地震損傷主要出現在主墩墩底與墩頂部位而主塔基本無損傷的現象。

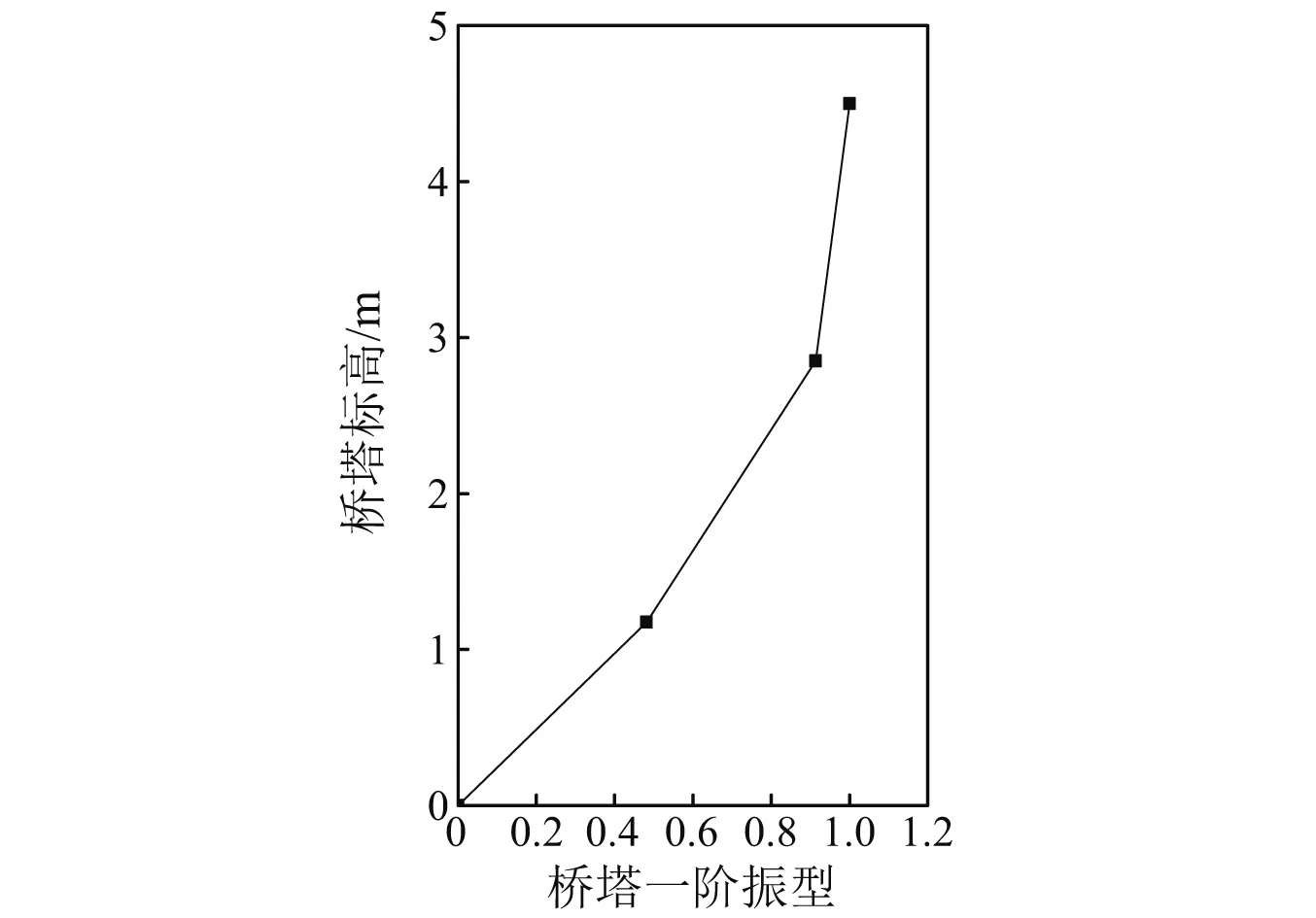
圖12 白噪聲工況下T2橋塔縱橋向一階振型圖Fig.12 First-order mode of T2 tower

本試驗在加載工況B開始前與峰值加速度0.30～1.50g的各工況結束后均采用了峰值加速度為0.10g的白噪聲進行掃頻試驗。表6所示的是以T2橋塔的塔頂測點加速度響應傳遞函數為例得到的結構一階自振周期和阻尼比隨臺面輸入PGA的變化。由表6可知，加載工況B開始前，結構一階周期仍為0.727 s，阻尼比仍為0.081，表明加載工況A結束后結構仍處于彈性范圍；當臺面輸入PGA在0.30～0.40g時，結構一階周期變為0.762 s，阻尼比逐漸增加，表明結構開始出現輕微剛度退化；當臺面輸入PGA在0.50～0.90g時，結構一階周期進一步增大，阻尼比雖然在0.60～0.90g時有一定減小，但可能是半功率帶寬法的誤差所致，總體仍維持在約0.13～0.14，較0.4g以前的阻尼比有較大提升，可見結構剛度發生進一步退化；當臺面輸入PGA在1.00～1.50g時，結構一階周期達到1.067 s，阻尼比急劇增大，表明結構地震損傷嚴重。

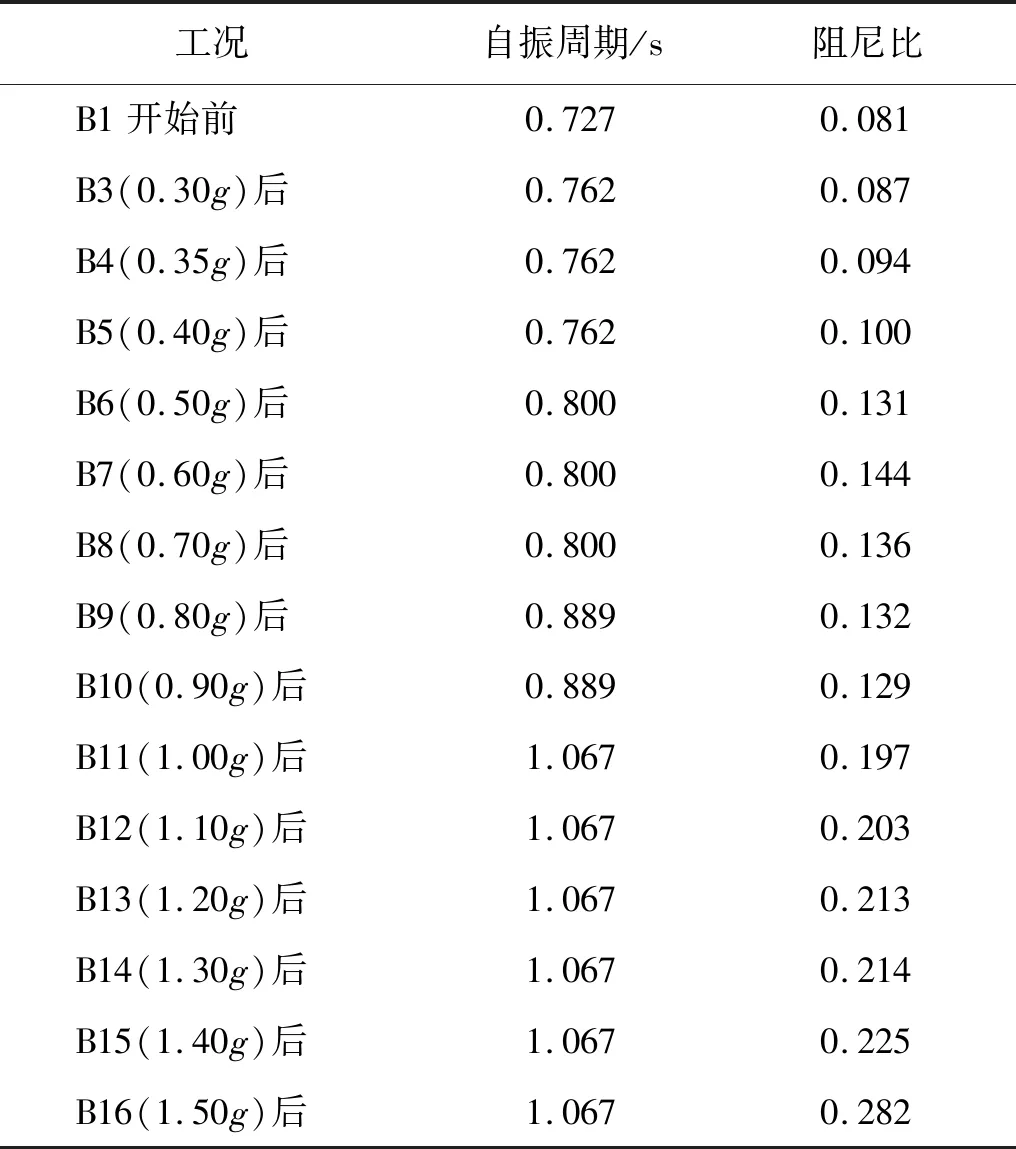
表6 試驗模型一階振型自振周期及阻尼比

3.3 位移響應

在縱橋向兩條地震波作用下，T2橋塔的主墩墩頂測點和主塔塔頂測點的最大位移響應隨臺面輸入PGA的變化關系如圖13所示。

由圖13可知，當臺面輸入PGA在0.1～0.3g時，場地人工波作用下的塔頂最大位移均略大于El Centro波，這是由于場地人工波與El Centro波的地震動特性不同，場地人工波的特征周期更長，長周期成分更豐富，激發的結構地震響應較大；當場地人工波的臺面輸入PGA為0.1～0.35g時，模型最大位移響應基本保持線性增長，表明結構整體處于彈性階段；當場地人工波的臺面輸入PGA達到0.4g時，最大位移曲線的斜率明顯增大，表明此時結構剛度有所下降，開始進入塑性階段；當場地人工波的臺面輸入PGA為0.5～1.5g時，主塔塔頂測點與主墩墩頂測點的位移反應雖然總體呈增長趨勢，但已不再保持線性增加，表明結構已逐步出現損傷；而對于不同臺面輸入PGA時，主塔塔頂測點與主墩墩頂測點的最大位移基本相同，表明在整個縱橋向的損傷發展過程中，包括彈性階段和屈服階段，矮塔斜拉橋的主塔自身變形都較小，塔頂縱向位移主要由主墩變形產生。

3.4 鋼筋應變響應

圖14顯示在不同臺面輸入PGA下,試驗模型T2橋塔主塔塔底、主墩墩頂及主墩墩底截面的所有被測縱筋的最大應變響應。

從圖14(a)可知，主墩墩底截面的縱筋應變在臺面輸入PGA為0.35g時基本達到鋼筋屈服應變0.002，表明此時結構剛要進入塑性階段；在臺面輸入PGA達到0.4g時，主墩墩底截面縱筋應變急劇增大至約0.005，鋼筋發生屈服，表明結構已進入塑性階段；在臺面輸入PGA為1.2～1.5g時，主墩墩底截面縱筋應變發生損壞，退出工作。

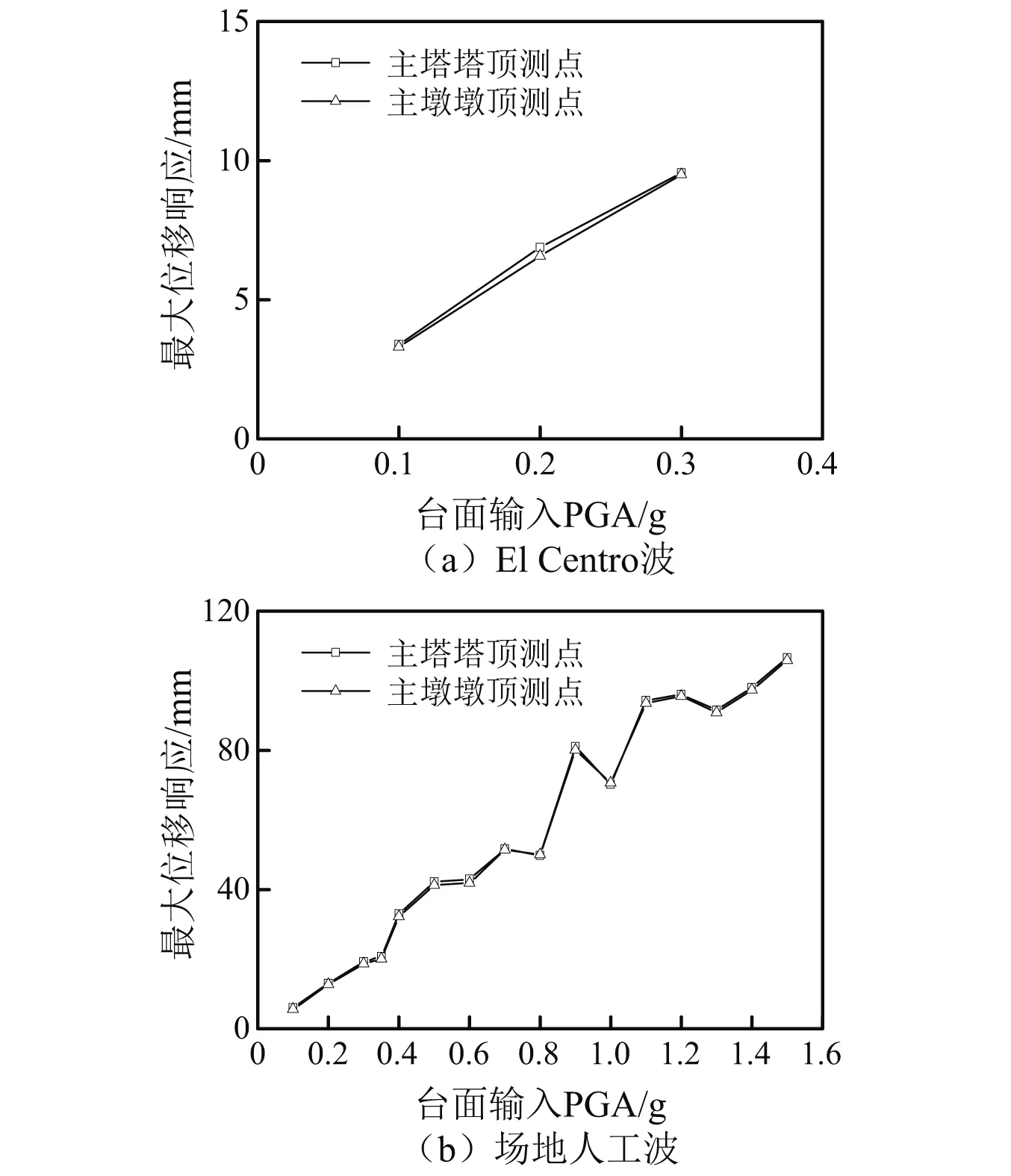
圖13 不同測點最大位移響應隨臺面輸入PGA變化曲線Fig.13 Maximum displacement of measuring points

從圖14(b)可知，主墩墩頂截面的縱筋應變在臺面輸入PGA為0.8g時基本達到鋼筋屈服應變0.002，表明此時主墩墩頂部位剛要進入塑性階段，這也驗證了試驗中觀察到主墩墩底截面比主墩墩頂截面先出現損傷的現象；而當臺面輸入PGA達到0.9g后，雖然臺面輸入PGA進一步增大，但主墩墩頂鋼筋應變基本不再增加,這主要是由于主墩墩底部位已形成塑性鉸，雙薄壁墩形式主墩的框架效應受到削弱，因此主墩墩頂部位的結構響應不再明顯變化。

從圖14(c)可見，主塔塔底截面的縱筋應變最大值約為0.000 8，遠小于鋼筋屈服應變0.002，表明主塔始終保持彈性狀態；當臺面輸入PGA為0.1～0.35g時，主塔塔底鋼筋應變基本隨臺面輸入PGA線性增大；當臺面輸入PGA達到0.4g后，主塔塔底鋼筋應變曲線斜率出現變緩，這是由于下部主墩墩底截面開始進入塑性，結構發生初步損傷；當臺面輸入PGA達到0.9g后，雖然臺面輸入PGA進一步增大，但主塔塔底鋼筋應變已基本不再增加，這是由于主墩墩底部位已形成塑性鉸，因此結構內力不再明顯增大。

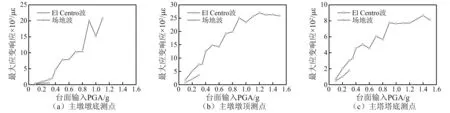
圖14 不同測點最大應變響應隨臺面輸入PGA變化曲線Fig.14 Maximum strain of measuring points

4 結 論

本文以一座典型的多塔矮塔斜拉橋為研究對象，根據相似理論設計了縮尺比為1∶20的全橋振動臺試驗模型，開展了縱橋向破壞性試驗，研究了矮塔斜拉橋的縱橋向地震損傷發展過程，主要研究結論如下：

(1) 隨著地震輸入PGA的增大，結構一階周期和阻尼比總體呈增大趨勢，試驗模型地震損傷逐漸加劇。在場地人工波PGA為1.5g時，主墩墩底部位核心混凝土壓潰，縱筋嚴重屈曲，主墩墩頂部位混凝土大面積剝落，縱筋輕微屈曲，而主塔表面未出現明顯裂縫，基本無損傷。

(2) 當場地人工波PGA<0.35g時，結構為彈性，超出0.35g后，主墩墩底截面縱筋應變最大值超過鋼筋屈服應變，結構進入塑性階段。

(3) 對于相同的PGA，由于場地人工波的特征周期更長，長周期成分更豐富，激發的結構地震響應均比El Centro波激發的結構地震響應大。