邊界摩擦條件下含有預緊的對合碟簧隔振單元的振動特性

惠安民，金映麗，張 磊，閆 明，王開平

(1.沈陽工業大學 機械工程學院，沈陽 110870； 2. 海軍研究院，北京 100161)

人們很早就意識到可以利用非線性機械元件變形時所產生的變剛度或變阻尼來改善隔振效果是一種非常有效的隔振措施[1]。但由于非線性泛函本構關系的復雜性，使得非線性結構在簡諧、隨機以及沖擊激勵下的響應計算存在一定的困難等原因，使得非線性隔振技術在前期應用的并不廣泛[2]。但隨著科學技術的不斷發展，人們對振動控制的要求不斷的提高，常規的線性隔振技術已無法滿足被動隔振的需要，因此非線性隔振技術在航空航天、機械、建筑、汽車等領域得到了較快的發展。

碟型彈簧(以下簡稱碟簧)，是一種碟型墊圈式彈簧，其自身具有體積小、承載能力高、加載均勻、緩沖性能良好、在一定條件下具有變剛度的特性，自身還可提供阻尼；可以將多片碟簧以不同的疊放方式，組合構成一種非線性彈性元件或裝置，而該類裝置由于碟簧受力變形過程中還同時存在Coulomb阻尼和黏性阻尼的特性[3]，因此在非線性隔振領域得到了較為廣泛的應用；就目前而言，國內外學者對碟簧以及碟簧類隔振裝置進行了大量的分析研究，其中，Almen等[4]系統地對等截面錐形碟簧進行了理論分析與計算研究，給出了碟簧自身幾何性質與其承載能力的關系，同時提出碟簧對合放置時，其內部結構的Coulomb阻尼系數最小；La Rosa等[5]、Saini[6]等基于Almen等的研究理論，通過計算分析，分別研究了線性變化截面與拋物線型截面的碟形彈簧的承載能力與變形的關系，并分別推導出了變截面錐型碟簧的載荷與形變公式；Ozaki等[7]通過數值方法對碟簧的摩擦邊界進行了靜態與動態分析；Patangtalo等[8-9]采用數值方法，對組合碟簧與開槽碟簧的載荷-位移曲線進行分析研究；高躍飛等[10]依據火炮系統沖擊緩沖與隔振的需求，建立了碟簧元件的非線性剛度模型，并對該模型的減振性能進行了分析計算；武銳等[11]通過試驗數據與有限元模型進行對比，修正有限元模型，并通過修正后的有限元模型，計算出了碟簧在不同組合形式下的靜剛度曲線；徐道臨等[12]通過有限元軟件分析碟型橡膠墊的負剛度特性并通過并聯正剛度特性彈性元件設計了一種準零剛度特性的低頻隔振系統。

綜合以上文獻可知，目前對于單一碟簧的靜力學性能、邊界摩擦條件下的準靜力學特性的研究以及應用仿真軟件分析常規、異形碟簧加載過程已有豐富的理論基礎和實際應用。而組合碟簧和碟簧類隔振裝置的振動特性多數文獻為簡化計算模型，仍將碟簧系統進行剛度或阻尼線性化處理，而線性化很大程度上改變了系統的動力學行為。且鮮有文獻針對對合碟簧隔振裝置在考慮邊界摩擦與承載條件下的非線性振動特性進行研究。因此，本文利用對合碟簧間的邊界摩擦，根據實際工程需求，設計一種碟簧隔振單元，并建立該隔振單元的振動微分方程，對其振動特性進行分析研究。

1 碟簧隔振單元

根據實際工程需求，設計了一種碟簧隔振單元，該隔振單元的原理，如圖1所示。

圖1 碟簧隔振單元Fig.1 Disc spring vibration isolator

從圖1可知，該隔振單元的結構特點為：多組對合碟簧串聯放置，充當彈性元件；且每對碟簧的對合面處布置有平墊圈，以保證拉壓過程中受力均勻以及每對對合碟簧都可以提供足夠的摩擦力；初始狀態時,碟簧內部存在預壓縮量，以保證高靜態低動態剛度特性；根據不同的承載條件，隔振單元的初始預緊力可以通過增減上下壓板厚度進行調節；上下壓板間充入適當硅油進行潤滑；不論外界傳遞給隔振單元的是軸向壓力還是拉力，都將被其轉化為對組合碟簧的壓力，這樣在保證結構緊湊的同時，也充分保證對合碟簧組不會出現分離現象。

圖2為上述隔振單元中的一對對合碟簧組的剖面圖，對合碟簧組包括兩個對合的碟簧，為提升系統穩定性并防止對合碟簧出現卡死現象，在對合碟簧中間，加入同材質的墊圈。碟簧為A系列無支撐碟型彈簧，其材料為60Si2Mn。

圖2 對合碟簧組Fig.2 Disc spring unit

圖2中：D和d分別為碟簧的外徑和內徑；t為碟簧的厚度；h0為碟片的最大壓縮量；H0為碟片的自由高度。

2 摩擦條件下碟簧隔振單元的剛度模型

根據Almen等的理論，碟簧的承載載荷與變形的推導需滿足以下三個假設：①碟簧在受到載荷作用后，其軸向截面不發生形變，仍為矩形，且此截面僅繞固定中性點回轉，因此徑向應力可忽略；②外部載荷和支撐面上的反作用力均沿內、外圓周分布，且碟簧材料本身為完全彈性；③忽略接觸表面上的摩擦力影響。由此可知，A系列無支撐面碟簧，其承載載荷與變形的理論計算公式為

(1)

通常，為簡化計算求解難度，式(1)可化簡為GB/T 1972—2005《蝶形彈簧》規范中的式(2)進行計算

(2)

根據對合碟簧組可知，碟簧間為串聯方式，因此對合碟簧組在受到相同在荷條件下，其位移量為單個碟簧的n倍，其剛度變為單片碟簧的1/n倍。其中，n為對合碟簧組中碟簧的個數。

2.1 考慮邊界摩擦影響的對合碟簧剛度模型

由于每對對合碟簧都有4個結合面，而每個結合面間都會產生摩擦，因此當碟簧個數n足夠大時，其結合面間所產生的摩擦力不應被忽略，應給予充分考慮。根據Ozaki等對碟簧加載過程中摩擦耗散的分析，單片碟簧軸向加載過程中的受力原理圖，如圖3所示。

圖3 單片碟簧軸向加載過程受力原理圖Fig.3 Principle diagram of axial loading process of single disc spring

圖3中:l為碟簧截面的對角線長；θ為約束面的法線與碟簧截面對角線的夾角；α為碟簧截面繞中性點O的旋轉角；Ff為受載壓縮后接觸面產生的摩擦力；μe為系統摩擦因數；ue為碟簧水平滑動距離。

根據幾何關系，其水平滑行距離與碟簧變形量間的關系可近似由式(3)計算

(3)

由此可知，摩擦損耗的能量增量ΔE與其水平滑行距離增量的關系為

ΔE=2Ff·Δue=2Fμe·Δue

(4)

根據式(4)可求得邊界摩擦條件下，摩擦力所提供的附加支持力ΔF為

(5)

因此，在不同摩擦因數條件下，單片碟簧加載過程中軸向壓縮距離f與附加支持力ΔF的關系曲線，如圖4所示。

圖4中，碟簧的幾何參數為：厚度t=0.5 mm；外徑D=28 mm；小徑d=10 mm；自由高度H0=1.15 mm；最大壓縮量h0=0.7 mm。

考慮邊界摩擦條件后，系統總承載如式(6)所示

Fz=F+n·ΔF

(6)

由此可知，當系統處于加載狀態時，系統由摩擦引起的附加支持力方向與碟簧彈性力方向一致，此時承載能力增大，系統剛度提高。當系統處于卸載狀態時，摩擦力提供的附加支持力與碟簧彈性力方向相反，系統剛度下降。從而使隔振系統產生遲滯特性。

圖4 碟簧加載過程軸向壓縮距離與附加載荷關系曲線Fig.4 Relationship between additional load and displacement

2.2 準靜載加載試驗

根據實際工程需求，選用圖4中碟簧的幾何參數作為隔振單元的碟簧參數，其中碟簧個數n=48。為保證碟簧隔振單元具有較高的承載能力，初始條件下設置預緊力為45 N。為驗證上述理論求解載荷過程的正確性，對該設計的隔振單元進行準靜態加載試驗，并與理論計算結果進行對比。

圖5為實測隔振單元的準靜態加載試驗的力與位移曲線與理論計算曲線的對比。

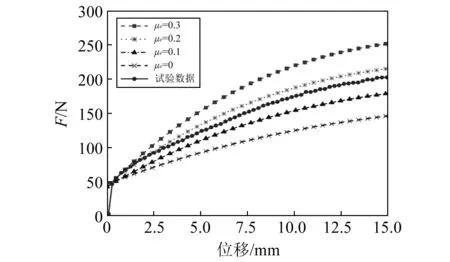
圖5 準靜態試驗實測曲線與理論計算曲線對比Fig.5 Comparison between measured curve of quasi-static test and theoretical calculation curve

由圖5可知，加載過程中，隨著摩擦因數的增大，系統的剛度受摩擦力的影響就越大，系統的剛度隨著摩擦因數的增大而增大。同時，考慮邊界摩擦條件后，根據該隔振單元的準靜態實測數據，系統摩擦因數μe約為0.15～0.2的理論計算值可以很好的預測出準靜態加載環境下該隔振抗沖單元的力與位移變化情況，該摩擦因數取值范圍與文獻[13]中吻合。當μe=0時，即系統內不存在摩擦，此時的力與位移曲線應為碟簧單元本身彈性力提供的剛度曲線。

對μe=0時的力與位移曲線進行擬合時發現：曲線可表達為位移的三次函數，即其剛度特性可表為

K1·x+K2·x2+K3·x3+α=F

(7)

式中：K1,K2,K3分別為非線性剛度的一次、二次與三次系數；α為碟簧隔振器初始預緊力；x為隔振單元的位移。碟簧隔振抗沖擊單元力與位移特性曲線擬合圖,如圖6所示。

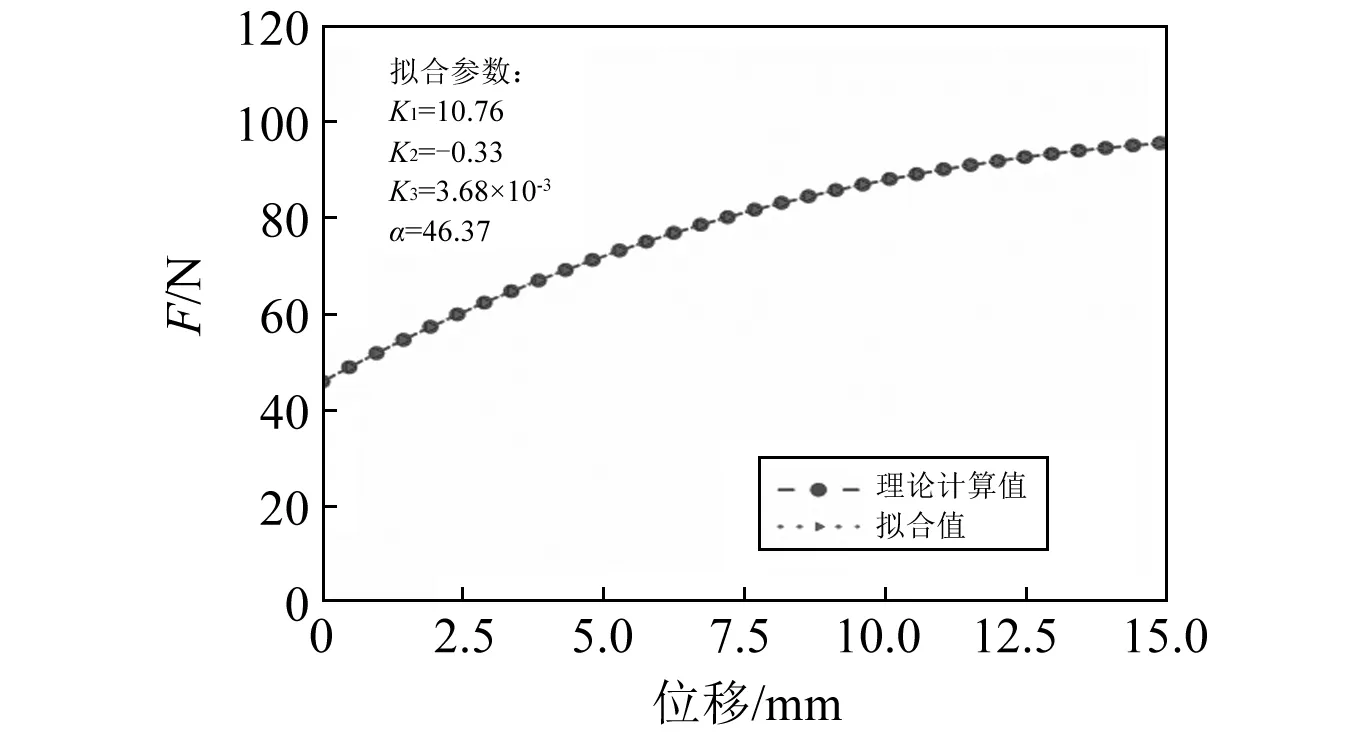
圖6 碟簧隔振抗沖單元力與位移曲線擬合圖Fig.6 Fitting diagram of force and displacement curve

顯然，當對合碟簧充當彈性元件時，系統剛度無法再應用線性模型進行準確的表達[14]。

3 碟簧隔振單元的動力學模型

通過邊界摩擦對系統附加支持力可知，該附加支持力的方向與系統的速度方向相反，因此可以應用符號函數對其進行描述，建立變剛度的碟簧-質量系統模型，其原理如圖7所示。

圖7 變剛度碟簧-質量系統原理圖Fig.7 Schematic diagram of nonlinear disc spring system

圖7中：M為系統質量;c為系統黏性阻尼系數;Kt為系統非線性剛度，其剛度變化規律符合式(7)；ΔFn為碟簧邊界摩擦引起的附加支持力總和，其值為n·ΔF。

3.1 碟簧隔振單元的自由振動

系統施加載荷后，其平衡位置x0處滿足靜剛度曲線式(7)，見圖7。為研究平衡位置x0附近的自由振動過程，令位移u=x+x0，則該碟簧-質量隔振系統自由振動條件下的微分方程為

(K1·u+K2·u2+K3·u3+α)=F

(8)

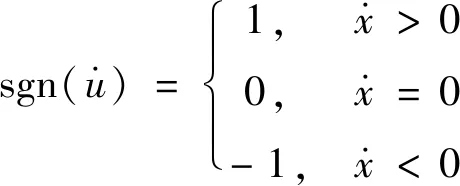
(9)

式中：(·)為時間的導數；由于x0為常數項，把位移u=x+x0代入式(8)中，整理可得式(10)

(10)

利用平均法思想，對式(11)進行求解，設方程解的形式為：x=a·cos(ψ)，ψ=t+θ；則可知

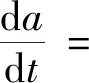
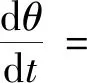
(12)

解式(12)的一階微分方程，并代回到方程解的形式中，可得非線性對合碟簧系統在自由振動條件下的近似振動方程

(13)

式中，a0和θ0的值由系統的初始條件確立。通過式(13)可知，該非線性系統的振動頻率不僅與剛度的一次方和承載質量有關，還與剛度的三次系數和初始運動狀態、系統黏性阻尼、附加支撐力均相關。為全面探求該碟簧系統的隔振性能，下面對該碟簧系統的受迫振動進行分析。

3.2 碟簧隔振單元的受迫振動

由于該隔振單元主要應用于基礎激勵下的隔振與抗沖擊防護，因此在考慮邊界摩擦條件以及承載質量為M條件下，建立其基礎激勵下的運動微分方程

(14)

(15)

f(σ)=σ+α1·σ2+α2·σ3

設非線性方程在Ω=1的主共振區域附近，其響應為

σ(τ)=A(τ)·cos(Ωτ-θ(τ))

(16)

式中，振幅A(τ)與相位θ(τ)為時間的慢變函數。根據Klotter[15]提出的對上述微分方程的求解方法，可應用式(17)計算其幅頻特性方程

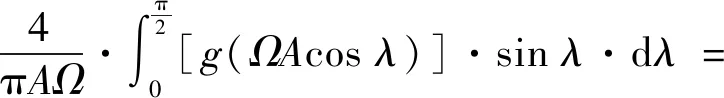
(17)

式中：A0為函數A(τ)的最大值；λ為虛擬積分變量；整理式(17)可得系統的幅頻特性方程為

(18)

同時，該系統的絕對位移傳遞率為系統質量M的最大位移x0與基礎的最大位移y0之比，即

全民健身是廣大人民群眾在閑暇時間開展的、以身體運動為主要手段、以提高健康水平為主要目的的體育活動形式[1]。據相關研究顯示，加拿大2000年有48%的人參加體育鍛煉，美國2005年“積極參加體育鍛煉”的人口比例是49%，芬蘭2005—2006年間有39%的成年人每周參與高強度鍛煉或5次以上中等強度鍛煉，而我國2014年20歲及以上經常參加體育鍛煉的人數為14.7%，與發達國家相比，我國全民健身的參與人數還處于較低水平[2]，不過近年來我國的健身人數已在逐步增長。本文基于創意理論視角，對全民健身新的參與方式進行分析，并提出相關建議，以期為新形勢下我國全民健身的發展提供借鑒。

(19)

由此可知，該隔振單元的幅頻特性、絕對位移傳遞率與非線性剛度二次項系數α1無關，而主要由非線性剛度三次項系數α2、黏性阻尼系數μ1、以及附加支持力系數μ2決定。

4 隔振參數對系統傳遞率的影響分析

為研究系統參數對該對合碟簧隔振單元隔振性能的影響，選用絕對位移傳遞率系數T′d(其值為20·logTd)描述系統隔振性能，并變換式(15)中相關系數。其具體過程如下。

4.1 小位移條件下的受迫振動

當系統的相對軸向位移z很小時，通過圖4可以看出系統內摩擦力提供的附加支持力ΔFn也很小，此時，附加支持力ΔFn對系統的影響也很較小。因此，小位移條件下，為研究該對合碟簧系統與非線性剛度的黏性阻尼系統間的差異，以及剛度非線性系數α2對隔振系統傳遞率的影響，進行如下比較。

應用matlab對式(17)的六次多項式求解，并計算不同參數下的位移傳遞率系數，如圖8所示。為小位移條件下，不同附加支持力系數μ2對系統位移傳遞率系數的影響：其中非線性剛度三次項系數α2=0.2、黏性阻尼系數μ1=0.2。

圖8 不同附加支持力系數μ2 對系統傳遞率的影響Fig.8 Influence of different additional supporting force coefficient μ2 on system transfer rate

從圖8可知，在位移較小且系統中附加支持力ΔFn不大的情況下，對合碟簧隔振單元的傳遞率曲線近似等于同等非線性剛度的黏性阻尼系統，附加支持力系數μ2僅改變了系統的脫離頻率Ωb，即隨著μ2的增大，系統脫離頻率隨之增大，但增大速率隨著μ2的增大而逐漸減小。

圖9為小位移條件下，非線性剛度三次項系數α2對系統位移傳遞率系數的影響。其中附加支持力系數μ2=0.05、黏性阻尼系數μ1=0.2。

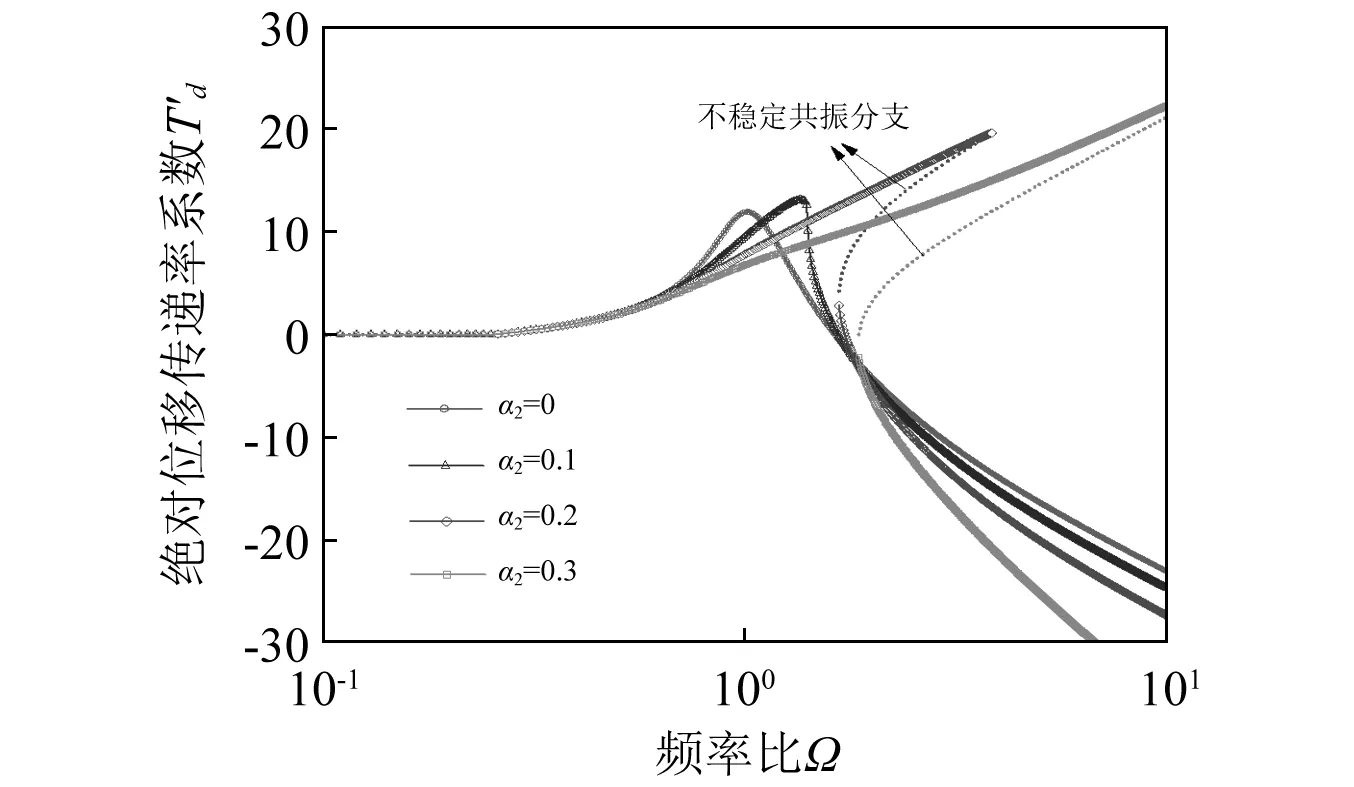
圖9 不同非線性剛度三次項系數α2對系統傳遞率的影響Fig.9 Influence of different nonlinear term coefficients α2 on system transfer rate

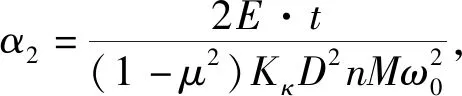
4.2 大位移條件下的受迫振動

當系統的相對軸向位移z較大，系統中的摩擦力所引起的附加支持力ΔFn足夠大且不可忽略時，為研究μ1與μ2對該對合碟簧隔振系統的隔振特性的影響，分別對不同系數條件下碟簧隔振單元進行求解計算，并繪制傳遞率曲線，如圖10所示。

圖10為剛度三次項系數α2=0.2、黏性阻尼系數μ1=0，以及附加支持力系數μ2分別等于0.1，0.5，1.3以及1.5的傳遞率曲線。從圖10可知，大位移情況下，系統的脫離頻率變化規律與小位移條件下的變化規律相似，即增大μ2的值，會使脫離頻率變大，但當μ2的值持續增大，使得脫離頻率接近隔振區臨界隔振頻率時，系統的左側傳遞率分支出現異常跳躍現象(見圖10(a))。當μ2的值繼續增大，系統傳遞率呈現的形式(見圖10(b))。此時，系統不會發生向共振分支的跳躍現象[16]，且在全頻域內，系統的傳遞率系數T′d≤0。

圖10 大位移條件下μ2對系統傳遞率的影響Fig.10 Influence of μ2 on system transfer rate under large displacement

同時，分別計算表1中的參數，以驗證大位移條件下，不同μ1值對對合碟簧隔振系統隔振效率的影響。

表1 計算相關參數Tab.1 Related parameters

將表1中的參數代入至幅頻特性方程式(18)，進行求解，并繪制傳遞系數曲線圖，僅當μ1較小時，觀察到如圖10中的異常跳躍現象，但當μ2足夠大時，均觀察到系統出現全頻域傳遞率系數T′d≤0的情況。不同μ1值中系統出現全頻域傳遞率系數T′d≤0時的傳遞率曲線，如圖11所示。由此可以發現隨著μ1值的增大，系統到達全頻域傳遞率系數T′d≤0狀態時所需的μ2值變小，較大的μ1值會改善共振狀態，使共振峰降低，但會影響高頻區的隔振效率。

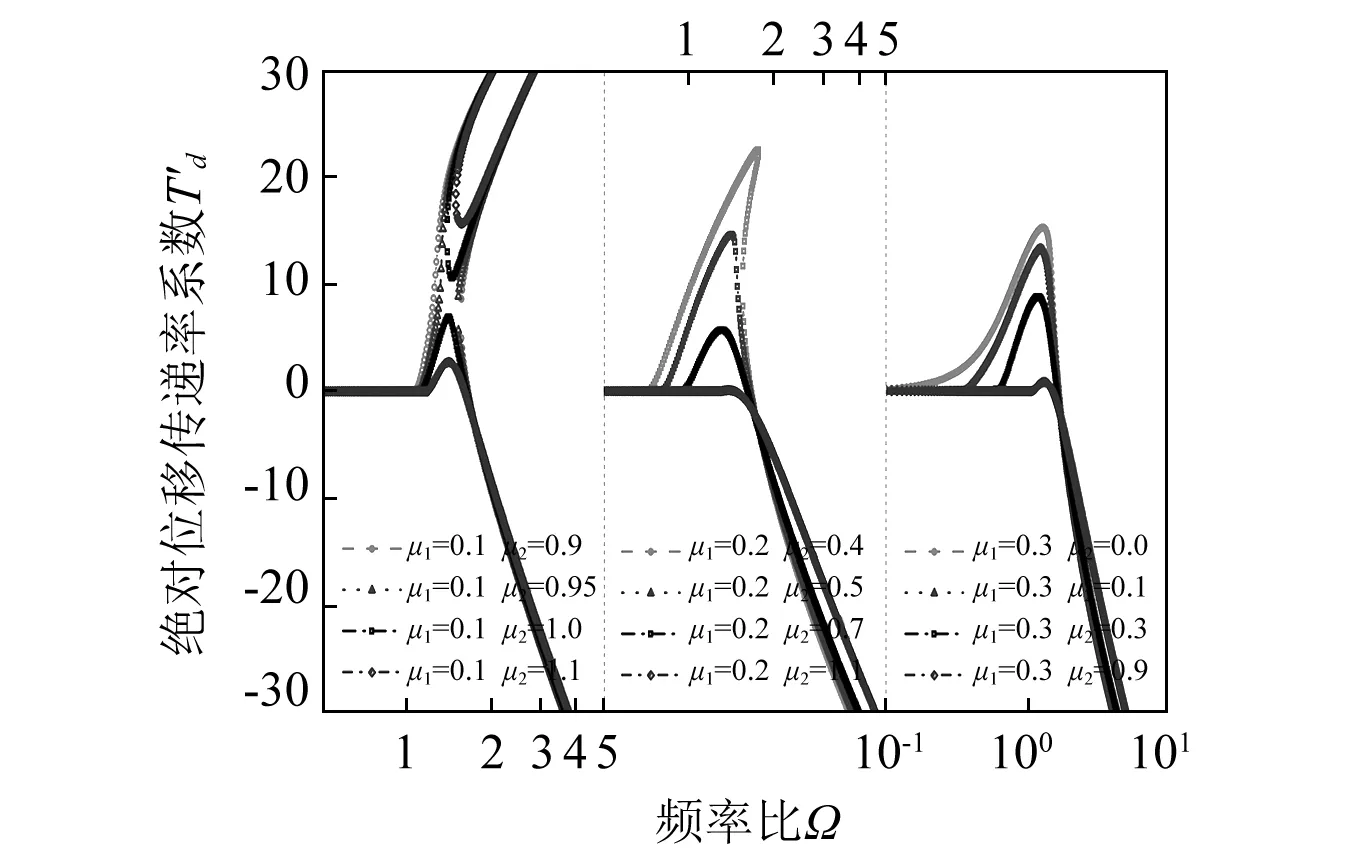
圖11 大位移條件下μ1對系統傳遞率的影響Fig.11 Influence of μ1 on system transfer rate under large displacement

5 結 論

(1)考慮邊界摩擦條件下的對合碟簧隔振單元，其內部摩擦會提供給系統一個額外的支持力，該支持力的方向與系統運動速度方向相反，且大小在一定范圍內與系統的相對位移成正相關。

(2)自由振動條件下，含有預緊的對合碟簧隔振單元的振動頻率不但與剛度的一次方系數和承載質量有關，與剛度的三次系數和初始運動狀態、系統黏性阻尼、附加支撐力均相關。

(3)小位移受迫振動條件下，該對合碟簧隔振系統可以簡化為非線性剛度的黏性阻尼系統，其附加支持力系數μ2僅影響系的統脫離頻率，且剛度三次項系數α2的值選取過大，不利于隔振。

(4)大位移受迫振動條件下，當系數μ1較小時，μ2的持續增大會使系統進入異常跳躍狀態和全頻域內的傳遞率系數T′d≤0狀態，且μ1值越大，到達兩種狀態所需的μ2值就越小。而當系數μ1的值較大時，μ1值會改善共振狀態，使共振峰降低，適當增大μ2值可使系統在全頻域內的傳遞率系數T′d≤0，但過大的μ1值會影響高頻隔振效果。