進氣系統空氣流量計布置數值研究

于洋磊，胡見，曾志新，董愚

(廣州汽車集團股份有限公司汽車工程研究院，廣東廣州 511434)

0 引言

作為汽車的重要組成部分，進氣系統主要負責將凈化后的空氣輸送進發動機燃燒室，氣流的大小和穩定性將對發動機的動力性、經濟性和整車排放等產生重要影響[1]。為此，在進氣系統中一般安裝有空氣流量計，用于監測輸送進發動機燃燒室內的空氣量，以此作為ECU計算點火時間和噴油時間的重要依據，從而讓發動機在各種工況下均可達到最佳的空燃比。為保證空氣流量計測量的空氣量具有準確性和代表性，對其布置的研究就變得極為重要。

CFD數值仿真是流體力學、數值分析和計算機結合的產物，是分析進氣系統流場的主要方法[2]。在驗證仿真模型及方法的基礎上，利用STAR-CCM+軟件，對不同插入角度、深度、軸向位置、管路入口圓角等因素影響下的空氣流量計性能進行了系統研究，獲得了各因素對空氣流量計性能的影響規律，所得結論對空氣流量計布置設計具有一定的指導意義。

1 模型建立

1.1 幾何模型

圖1是進氣系統的三維數模，由進氣管、空氣濾清器、空氣流量計、進氣軟管、進氣硬管等組成。其中，空氣流量計位于空氣濾清器上殼體出口管路段。

圖1 進氣系統數模

圖2是不同布置位置下的空氣流量計示意圖。其中，圖2(a)為不同插入角度的空氣流量計位置示意圖，以+Z方向為基準，在YZ平面內順時針旋轉角度α，得到不同插入角度的空氣流量計布置；圖2(b)為不同插入深度的空氣流量計位置示意圖，在YZ平面內，以空氣濾清器上殼體出口管路段內表面最大Z坐標處為基準，向下插入深度h，得到不同插入深度的空氣流量計布置；圖2(c)為不同軸向距離的空氣流量計位置示意圖，為便于觀察，以線框圖進行展示。在XZ平面內，黑色空氣流量計位置處于最左側，以其氣流入口為基準，向-X方向移動距離d，得到不同軸向距離的空氣流量計布置；圖2(d)為不同圓角半徑的示意圖，圓角位于空氣濾清器上殼體出口處，其圓角半徑為r。

圖2 不同布置位置的空氣流量計示意

通過改變插入角度α、插入深度h、軸向距離d和圓角半徑r等幾何參數以及進氣系統入口質量流量q，設計不同的物理模型來進行研究，變量參數設置范圍見表1。

表1 變量參數范圍

采用空氣流量計入口速度偏差vd和湍流強度I對空氣流量計布置性能進行評判。

(1)

(2)

式中:vmax為空氣流量計入口最大速度，m/s；vmin為空氣流量計入口最小速度，m/s；Re為雷諾數。

1.2 仿真模型

圖3為進氣系統流體域網格模型。在劃分網格前首先進行幾何處理，對模型進行適當簡化，且為了考慮節流損失，在進氣口建立半球形包絡面，其半徑為進氣口水力直徑的2倍。幾何處理后進行面網格劃分，經過網格無關性分析，采用網格平均尺寸為2 mm，局部物理梯度較大的地方縮小至0.5～1 mm，物理梯度變化平緩的采用3 mm尺寸網格。基于面網格，采用STAR-CCM+軟件生成其特有的“蜂窩”狀多面體網格，具有更多相鄰單元，對于梯度計算和流動狀況預測更準確，收斂速度更快[3]。對于近壁面區域，設置邊界層，厚度為2 mm，為控制體網格數量，設置增長率為1.2。網格總數約為350萬。

圖3 網格模型示意

由于進氣系統額定流量為460 m3/h，最大速度小于100 m/s，馬赫數Ma<0.3，氣體可被認為是不可壓縮流體的湍流運動。湍流運動是一種非常復雜的非線性運動，如圖4所示，其數值模擬分為直接數值模擬法和非直接數值模擬法兩大類[4]。

圖4 湍流數值模擬方法

直接數值模擬法(DNS)是指對流場的湍流運動不做任何形式上的簡化，將流動域直接用瞬態的N-S方程進行求解。用此法進行計算可以得到比用非直接法計算更加精確的數值模擬結果[5]。但限于技術條件，還無法在計算機上直接進行計算。非直接數值模擬法是指先對湍流運動進行簡化，再計算湍流脈動特性。依簡化方法不同，其可分為Reynolds平均法、大渦模擬法以及統計平均法[6]。其中，標準k-ε模型目前被廣泛應用于傳熱、燃燒以及發動機進氣系統內的氣體流動的計算等，是工程計算領域內應用最廣的一種湍流模型[7]。

2 仿真方法驗證

為驗證仿真方法精度，在空濾器性能試驗臺上進行了不同入口流量下的進氣系統壓損試驗。試驗時環境介質參數見表2。

表2 環境介質參數

依據試驗參數，進行相同條件下的數值仿真，入口條件設為壓力邊界，出口設為質量流量邊界。進氣系統視為絕熱系統，壁面條件絕熱、無滑移。

表3為仿真壓損與試驗壓損的對比表，相對誤差最大為5.05%，仿真方法具有較高的精度，該方法具有較高的可行性。

表3 仿真與試驗結果對比

3 結果與分析

3.1 插入角度的影響

圖5是不同插入角度的空氣流量計在不同的進氣系統流量時的入口速度偏差云圖，X坐標為插入角度α，Y坐標為進氣系統流量q，Z坐標為空氣流量計入口速度偏差vd。在0°～30°區間，不同流量q下的速度偏差vd均隨插入角度α的增大而大幅減小；在30°～60°區間，速度偏差vd減幅變小，且隨著流量q的增大，減幅逐漸收窄，在額定流量460 m3/h時反而微增，最小值為35.58%；在60°～180°區間，對于低流量區，速度偏差vd隨插入角度α增大而增大，最大值為48.93%，在中高流量區，速度偏差vd在120°～150°區間出現減小，且隨流量q增大，減幅呈增大趨勢。表明插入角度α對速度偏差vd影響明顯，在高流量區，速度偏差vd相對更小，且存在最佳插入角度區間，使得不同流量下的速度偏差均較小。

圖5 速度偏差云圖

圖6是不同插入角度的空氣流量計在不同的進氣系統流量時的入口湍流強度云圖，X坐標為插入角度α，Y坐標為進氣系統流量q，Z坐標為空氣流量計入口湍流強度I。在0°～120°區間，湍流強度I隨插入角度α增大而小幅增大，在120°～180°區間，湍流強度I隨插入角度α增大而小幅減小。且在低流量區，湍流強度I存在最大值，為5.64%，隨流量q逐漸增大，湍流強度I逐漸減小，在高流量區存在最小值，為4.43%。表明湍流強度I受插入角度α影響較小。

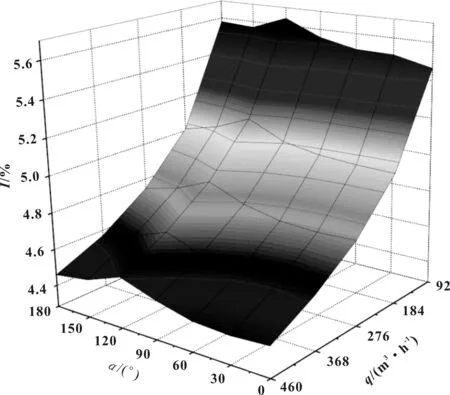
圖6 湍流強度云圖

3.2 插入深度的影響

圖7是不同插入深度的空氣流量計在不同的進氣系統流量時的入口速度偏差云圖，X坐標為插入深度h，Y坐標為進氣系統流量q，Z坐標為空氣流量計入口速度偏差vd。在插入深度h較小且處于低流量區時，速度偏差vd存在最大值，為63.01%。在9～18 mm區間，速度偏差vd隨插入深度h增大而大幅減小；在18～27 mm區間，速度偏差vd趨于平緩；在27～36 mm區間，速度偏差vd小幅減小；在36～45 mm區間，速度偏差vd大幅減小且在高流量區出現最小值為31.73%。在45～54 mm區間，速度偏差vd在低流量區趨于平緩，在高流量區小幅增大。表明插入深度h對速度偏差vd影響明顯，最大與最小速度偏差之差為31.28%，且在高流量區，速度偏差vd相對更小。存在最佳插入深度區間，使得不同流量下的速度偏差均較小。

圖7 速度偏差云圖

圖8是不同插入深度的空氣流量計在不同的進氣系統流量時的入口湍流強度云圖，X坐標為插入深度h，Y坐標為進氣系統流量q，Z坐標為空氣流量計入口湍流強度I。隨插入深度h增加，湍流強度I波動小幅減小。在低流量區，湍流強度I存在最大值為5.68%，隨流量q逐漸增大，湍流強度I逐漸減小，在高流量區存在最小值為4.37%。表明湍流強度I受插入深度h影響較小。

圖8 湍流強度云圖

3.3 不同軸向距離的影響

圖9是不同軸向距離的空氣流量計在不同的進氣系統流量時的入口速度偏差云圖，X坐標為軸向距離d，Y坐標為進氣系統流量q，Z坐標為空氣流量計入口速度偏差vd。隨軸向距離d增加，速度偏差vd不斷增大，最大值為80.52%，且在軸向距離處于較大時，速度偏差vd增大更快。即空氣流量計越靠近空氣濾清器上殼體出口處，其入口處速度偏差越大。隨流量q增加，速度偏差vd小幅減小，最小值為38.01%。表明軸向距離h對速度偏差影響很大，最大與最小速度偏差vd之差為42.51%。

圖9 速度偏差云圖

圖10是不同軸向距離的空氣流量計在不同的進氣系統流量時的入口湍流強度云圖，X坐標為軸向距離d，Y坐標為進氣系統流量q，Z坐標為空氣流量計入口湍流強度I。在低流量區，湍流強度I隨軸向距離增加而波動增大，在中高流量區，湍流強度I隨軸向距離增加而不斷增大。在低流量區，湍流強度I存在最大值，為5.69%，隨流量q逐漸增大，湍流強度I逐漸減小，在高流量區存在最小值，為4.39%。

圖10 湍流強度云圖

3.4 不同圓角半徑的影響

圖11是不同圓角半徑時的空氣流量計在不同的進氣系統流量時的入口速度偏差云圖，X坐標為圓角半徑r，Y坐標為進氣系統流量q，Z坐標為空氣流量計入口速度偏差vd。在中低流量區，當r處于0～3 mm區間時，速度偏差vd存在最大值，為47.29%，且速度偏差vd隨圓角半徑r增大而大幅減小，當r處于3～6 mm區間時，速度偏差vd趨于平緩，且在5～6 mm區間時有小幅增大。在高流量區，當r處于0～2 mm區間時，速度偏差vd隨圓角半徑r增大而大幅減小，當r處于2～3 mm區間時，速度偏差vd小幅增大，而后逐漸減小，在4～5 mm區間趨于平緩，且達到最小值，為34.48%，在5～6 mm區間，速度偏差vd增大。表明圓角半徑r對速度偏差vd影響較大，且并不是一味增大r就可減小速度偏差vd，存在最佳圓角半徑使得速度偏差vd在不同流量下均為最小。

圖11 速度偏差云圖

圖12是不同圓角半徑時的空氣流量計在不同的進氣系統流量時的入口湍流強度云圖，X坐標為圓角半徑r，Y坐標為進氣系統流量q，Z坐標為空氣流量計入口湍流強度I。在r處于0～4 mm區間時，隨圓角半徑r增加，湍流強度I幾乎不變，在4～5 mm區間時，湍流強度I增加，且在低流量區增幅相對明顯，而后在5～6 mm區間減小。表明圓角半徑r對湍流強度I影響較小。

圖12 湍流強度云圖

4 結論

(1)采用標準k-ε模型對進氣系統流場進行數值仿真，并與試驗進行對比，驗證了該數值方法的可行性。

(2)插入角度α和插入深度h對速度偏差vd影響明顯，且在高流量區，速度偏差vd相對更小，存在最佳插入角度和最佳插入深度區間，使得不同流量下的速度偏差均較小。湍流強度I受其影響較小。

(3)軸向距離h對速度偏差影響極大，越靠近空氣濾清器上殼體出口處，其入口處速度偏差越大，最大與最小速度偏差vd之差為42.51%。且湍流強度I隨軸向距離增加而呈增大趨勢。

(4)圓角半徑r對速度偏差vd影響較大，且并不是一味增大r就可減小速度偏差vd，存在最佳圓角半徑使得速度偏差vd在不同流量下均為最小。湍流強度I受其影響較小。