化歸思想在高中函數中的簡單應用

楊金諾

(黑龍江省伊春市第一中學 153000)

一、化歸思想概述

函數問題側重于解決實際問題，化歸思想講究的也就是實際運用.在學習的過程中，知識點是有限的，但是題型是無限的，不同于以往的“問題—解決—新問題—解決”的解題思路，化歸思想講究的是“知識點—問題—新問題—知識點”的解決方式.用已知的定義新的知識，并解決新的問題，就是化歸思想的核心.在解題過程中，可以運用多種方式和方法，進而實現解題的目的.

二、化歸思想的意義

化歸思想可以歸為唯物主義的觀點之一，在唯物主義中，將抽象的物體具體化，復雜的問題簡單化，化整為零是其核心思想之一.化歸思想在解題的時候強調轉化，眾所周知，任何數學思想都是在解題和學習的過程中不斷總結和歸納出來的，在解題過程中我們追求的是速度和準確率，而化歸思想可以很好地滿足該條件.

高中數學學習中，函數是十分重要的學習對象之一，高中的函數包括三角函數、對數函數、反比例函數等八種函數.我們解題時會發現基本的函數會演變成各種各樣的形式，比如復合函數、復數函數或者是抽象函數等，如何運用基本的函數形式來解決這類比較復雜的函數就顯得十分重要.此時就可以考慮利用化歸思想，將函數轉化為基本函數的形式，利用函數的性質和特點，或者是圖象等方式解決問題.

三、化歸思想在函數中的應用

化歸思想在函數解題中十分常見，為了更好地了解其在解題過程中的重要性，我們可以通過具體的例題進行分析.

1.已知推算未知

在解函數題過程中，我們常常會遇見陌生的函數題型，化歸思想的基礎就是將未知的問題轉為已知的問題.比如我們在解三角函數相關的問題時，可以考慮將其轉化為二次函數等簡單的函數，利用二次函數的性質進行求解.這樣就可以將復雜抽象的問題簡單化、具體化.不僅可以很好地解決問題，還可以加深對已學知識的理解和運用.例如在學習三角函數時，最常見的就是證明題.

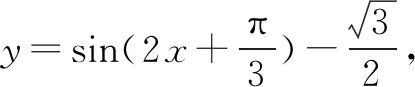
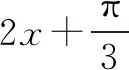
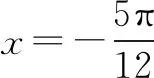
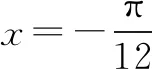
2.數形結合的方法

數形結合的方法也是我們解題時最常用的方法.因為數字是抽象的符號，但是數據過多的時候，我們就很難理清楚各個數據之間的關系,過多的數據會導致我們忽略一些數據，而在解題過程中，任何一個數據都有著很大的意義.通過數形結合，一方面可以使得抽象的問題具體化，另一方面可以使得數據的獲取更加全面.

數字與圖形自古就有，很多時候可以互相轉化.函數的一個特點就是抽象，雖然它能解決具體問題，但是解決過程卻十分抽象.為了更好地掌握函數，通過數形結合方法將代數問題轉化成幾何問題，顯得更加生動和直觀.

例2關于x的方程2x2-3x-2k=0在(-1, 1)內有一個實根，則k的取值范圍是什么？

該題目是求k的取值范圍，但是題干中的方程中還含有一個變量x，我們可以通過轉化2x2-3x-2k=0，使其變成函數y=2x2-3x，這樣一來，我們就將題目變成求解y=2x2-3x和函數y=2k的交點個數問題.

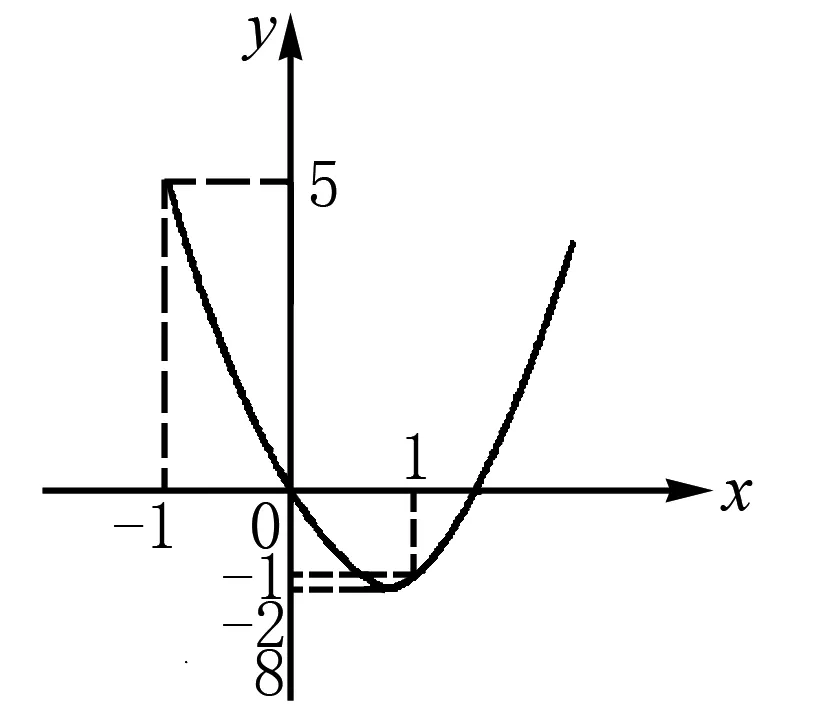
圖1

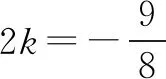
在解這一類題目過程中，如果采用單純的解題方式，很容易造成漏解的情況，但是在采用數形結合的方法后，就顯得一目了然.

3.復雜變量簡單化

在解函數題的過程中，當涉及到過多變量的情況時，題目就會顯得十分繁瑣，通過化歸思想中變量轉化的方法，將復雜的變量簡單化可以讓我們更好地理解題意，降低錯誤率.

例3若cos2θ+2msinθ-2m-2<0恒成立，試求實數m的取值范圍.

該題目是求m的取值范圍，但是題干的條件中除了m之外，還有sinθ和cosθ兩個函數，這樣一來，在這個題目中一共有三個變量，而我們掌握的是二元函數，所以考慮將題目中的函數轉化為二元函數.

通過轉化變量的方法，令sinθ=t，則cos2θ=1-sin2x，于是f(t)=t2-2mt+2m+1.

根據題目的要求，只要滿足f(t)>0在[-1，1]上恒成立即可求實數m的取值范圍.

解析令sinθ=t，可以得出，要想cos2θ+2msinθ-2m-2<0恒成立，可以通過轉化變量，設f(t)=t2-2mt+2m+1，則只要f(t)>0在[-1，1]上恒成立.

由于f(t)=(t-m)2+2m+1-m2(-1≤t≤1)，所以只要f(t)的最小值大于零即可.

若m<-1，則當t=-1時，f(t)min=2+4m，令2+4m>0，得m>-0.5，這與m<-1矛盾，故舍去；

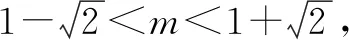
若m>1，則當t=1時，f(t)min=2，所以m>1.

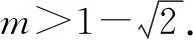
這個題目原本十分復雜，但是在轉化成二次函數之后，題干部分就顯得十分簡單明了，這樣就可以很好地降低解題的難度.

4.正面問題反面化

正面的問題反面化也就相當于運用了矛盾的思維.在解數學題時，經常會遇見題干十分簡單，但是卻無從下手的情況；或者是采用常規的解題方式十分麻煩，而且很難達到我們想要的結果.為了更好地解決問題，我們可以采用化歸思想中的反向思考的方式，也就是我們常說的逆向思維.

例4已知函數f(x)滿足：f2(x)-2f(x)f(x+1)+2f(x+1)=0(x∈R)，證明：f(x)不可能為正比例函數.

根據題目的要求，我們要證明f(x)不可能為正比例函數，首先就是利用化歸思想，將該函數和正比例函數的相關性質關聯起來，然后利用函數轉化的思想，將其轉化為一般的函數.假設f(x)=kx(k≠0),代入f2(x)-2f(x)f(x+1)+2f(x+1)=0,得-kx2+(2k-2k2)x+2k=0對任意x恒成立，故必有k=0，但由題設知k≠0，所以假設不成立.所以f(x)不可能為正比例函數.

在解題時，我們的思維一定不能局限于課堂上的知識或者是已知的知識，更重要的是融會貫通，這樣才可以更好地解決問題.

5.隱藏條件明顯化

函數解題的過程中，很多條件都是隱藏存在的，針對這一類情況，我們可以通過知識之間的聯系融會貫通，充分利用這些條件，達到解題的目的.

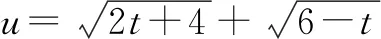
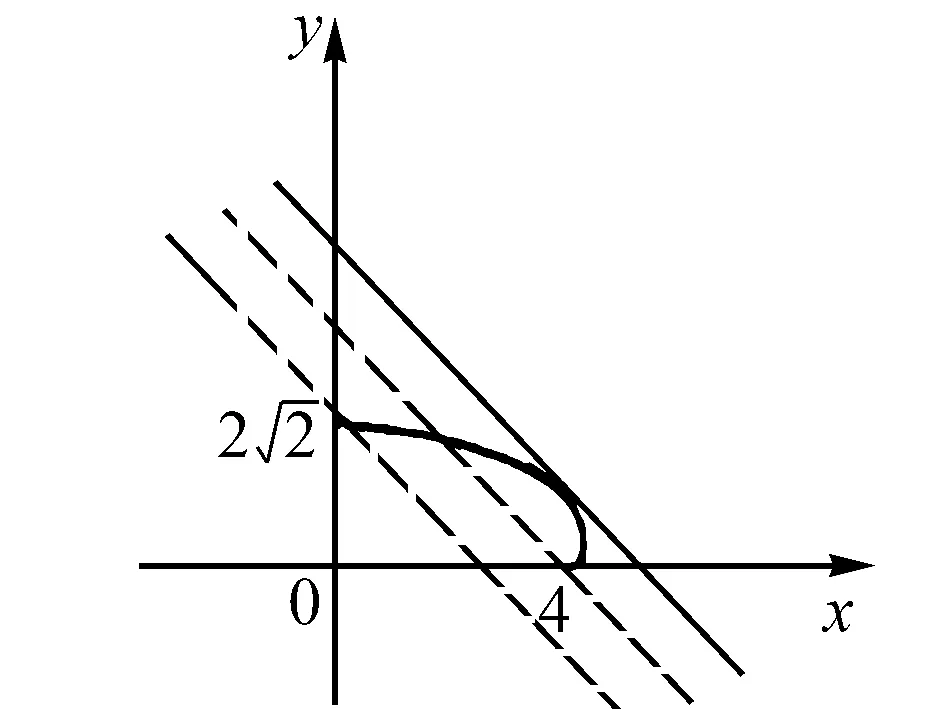
圖2

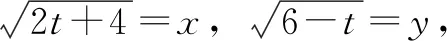
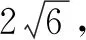
化歸思想在很多時候和數學中的轉化思想十分相近，但是又不完全一樣，它側重的是一種歸納，是對已學和已知的知識的歸納.這樣在遇見新的問題或者是復雜的問題時，也可以很好地解決.要想很好地掌握這種數學思想，最基礎的就是多練習、多思考，才可以很好地運用化規思想.