感壓膜片預張力對電容薄膜真空規輸出特性的影響

賈春旺，陳叔平*，成永軍，孫雯君，裴曉強，孟 岳，金樹峰，楊 雯，趙高逸

（1.蘭州理工大學石油化工學院，蘭州 730050；2.蘭州空間技術物理研究所，蘭州 730000）

關鍵字：電容薄膜真空規；感壓膜片；預張力；有限元分析；輸出電容

0 引言

隨著我國科學技術的發展，科學試驗和生產工藝對真空測量準確度的要求越來越高，這對真空度測量與校準提出了更高的要求，準確測量真空度顯得尤為重要[1]。電容薄膜真空規（CDG）相比其他試件模型，具有使用方便、延遲小、精度高、測量結果與氣體種類無關、重復性能好的優點[2]，作為中、低真空測量最重要的真空規之一，被廣泛用于航空航天、工業生產、重大科學儀器等領域的低真空測量，并可作為粗低真空的副標準和傳遞標準[3?5]。

對于薄膜器件，使用中若不施加或施加較低數值的預張力，會導致薄膜出現褶皺，承載后易出現變形過大的現象，并且在外界激勵作用下，容易發生振動；而預張力過大，會增加安裝難度，薄膜承載后，會造成應力過大等缺點。因此，為保證薄膜的平整度及承載能力，增加其穩定性，往往先使薄膜受到均勻的張力，然后再對其邊緣加以固定[6]。感壓膜片是電容薄膜真空規的核心部件，通常具有較大的寬厚比[7]，安裝時亦須施加預張力。預張力大小會影響感壓膜片的撓度，進而影響真空規的輸出特性，因此，必須考慮預張力對真空規性能的影響問題。

本文以電容薄膜真空規電容感應模塊為研究對象，結合COMSOL Multiphysics軟件及電容器電容理論計算方法，對受預張力的感壓膜片所構成的電容感應模塊進行建模分析，研究預張力對電容薄膜真空規輸出特性的影響，為后續的研究及設計提供一定的參考。

1 理論模型

圖1為電容薄膜真空規基本結構。主要由進氣管、感壓膜片、固定極板、固定基底、外殼體等組成。感壓膜片與進氣管連接一側為測量室，另一側為真空腔。

電容感應模塊主要包含感壓膜片、固定極板及真空腔，感壓膜片為上極板，固定極板為下極板，兩極板間為真空狀態。電容薄膜真空規基于變極距式平行板電容器結構制作，當感壓膜片受到壓力p作用時發生形變，導致兩極板初始間距d減小，電容增大，電容值與壓力一一對應，通過電容檢測電路檢測微小電容變化量，然后使用適當的測量轉換電路將電容的變化轉換為電壓信號，完成壓力的測量[8?9]。

1.1 初始電容

初始電容是指無外界壓力作用時電容薄膜真空規輸出的電容值，此時，感壓膜片撓度為零，與固定極板平行。電容按平行板電容器計算，表達式為：

式中：C0為初始電容，pF；ε0為真空介電常數，數值為8.85×10?12F∕m；b為固定極板半徑，mm。

1.2 可變電容

當受到外界壓力作用時，感壓膜片發生形變，致使兩極板間距減小，輸出電容發生變化。膜片的形變遵循一定的撓度曲面方程，設膜片位于r，θ平面，膜片形變后與固定極板之間的電容可按下式計算：

式中：C為可變電容，pF；εr為介質的介電常數，真空條件下εr=1；S為極板相對面積，mm2；r為膜片中心到膜片上任意一點的距離（0≤r≤b），mm；ω（r）為膜片變形后的撓度輪廓，可根據撓度形狀函數確定[9]：

式中：ω0為膜片中心撓度，mm；a為膜片半徑，mm。

將式（3）代入式（2）得：

由上式可知，計算可變電容不僅要知道真空介電常數、極板相對面積與極板間距，還須知道感壓膜片的中心撓度。施加預張力的感壓膜片在均布載荷作用下其中心撓度可由式（5）求得[10]：

式中：p為薄膜所受壓力，Pa；E為彈性模量，GPa；μ為泊松比；t為薄膜厚度，mm；σ0為施加于感壓膜片的預張力，MPa。

2 電容薄膜真空規輸出電容仿真

電容薄膜真空規的輸出電容仿真包含了電場和力場兩個物理場，必須通過耦合場來分析，與其他有限元分析軟件相比，COMSOL專注于多物理場耦合的建模與仿真，將多個物理場封裝成不同的模塊，使得分析結果更加貼近實際。選擇COMSOL中的機電模塊（emi）建立幾何模型，它同時包含了靜電場、力場和移動網格功能，無須考慮各個物理場之間的耦合。與理論計算過程相比，COMSOL仿真能同時獲得輸出電容、電勢分布、撓度分布、應力應變分布等結果，并且能夠很好地解決感壓膜片在壓力作用下的非線性問題。本文所建的幾何模型分為三部分：感壓膜片、真空腔和固定極板。

2.1 模型建立

以現有的測量上限為1.33 kPa的電容薄膜真空規為對象，取感壓膜片直徑為72 mm，厚度為45μm，材料選用Inconel 600合金；固定極板直徑為39 mm，厚度為3μm，材料選用Ag；兩極板間距為250μm。可變電容仿真主要涵蓋力場和電場，設置材料的彈性模量、密度、泊松比及相對介電常數，由于電容值的大小與兩極板介電常數無關，故對兩極板介電常數不作設置，表1為材料參數。采用用戶控制網格方式建立網格劃分模型，通過設置單元最大尺寸，形成掃掠網格。該有限元模型主要以六面體網格為主，網格單元數為68 429，結點數為98 713，電容感應模塊的網格劃分模型如圖2所示。

表1 電容感應模塊材料參數Tab.1 Material parameter of capacitive sensing module

圖2 電容感應模塊網格劃分模型Fig.2 Mesh model of capacitive sensing module

2.2 邊界條件

針對上述網格劃分模型，應用COMSOL軟件機電模塊模擬施加預張力的感壓膜片輸出電容隨壓力的變化。邊界條件分為力場邊界條件與電場邊界條件，力場邊界條件包括約束與載荷的大小及位置，電場邊界條件包括終端電勢與接地設置。對于施加預張力的感壓膜片，張拉膜片的外邊界是獲得均勻張力的有效方法，在膜片外邊界施加指定位移約束，將預張力等效為膜片的徑向位移。在薄膜上下兩側施加壓力，一面為待測壓力，一面為參考腔壓力。理論情況下，參考腔為真空狀態，但實際情況下，由于材料表面的氣體附著及長時間靜置，腔體會有一定程度漏氣，故參考腔壓力一般維持在10?4Pa。在壓力作用下感壓膜片中心撓度遠大于膜片厚度，為大撓度模型，故在分析前啟用非線性命令，以準確描述膜片在大撓度情形下的應變情況。將感壓膜片接地，電勢為0 V，設置固定極板終端電壓為10 V，兩者構成電容器。

3 結果分析

3.1 不同預張力下輸出電容

為便于分析預張力對輸出電容的影響，分別對感壓膜片施加30 MPa、40 MPa、50 MPa、60 MPa、70 MPa的預張力。針對每組預張力，在0～1 330 Pa內，以0 Pa為起點，133 Pa為步長，選取10組待測壓力分別施加于感壓膜片，并通過理論計算，得到不同預張力下輸出電容的理論解，并與COMSOL軟件求得的仿真解進行對比驗證。不考慮寄生電容及電場邊緣效應的影響，仿真所得到的不同預張力下輸出電容的仿真解（C1、C2、C3、C4、C5）與用式（4）求得的理論解（C1′、C2′、C3′、C4′、C5′）對比，并求得相對誤差（δ），如表2所列。當待測壓力為0 Pa時，輸出電容為初始電容，仿真結果為42.88 pF，通過式（1）求得的理論結果為42.27 pF，相對誤差為1.44%。

由表2可知，當待測壓力變化時，輸出電容仿真解與理論解的最大誤差為16.6%，最小誤差為2.2%，總體表現為壓力越大，相對誤差越大；預張力越大，相對誤差越小的趨勢。這是由于在電容理論計算式中，電容的準確計算取決于撓度形狀函數的準確性，而式（3）所示的撓度形狀函數為近似函數，只能近似描述預張力膜片的撓度分布；另一方面是由于壓力越大，膜片非線性形變越大，而仿真計算過程中網格數量有限，計算精度下降，故產生累計誤差。

仿真同時得到了不同預張力下感壓膜片的中心撓度，與用式（5）求得的理論解對比，撓度的最大誤差為7.1%，最小誤差為2.5%，總體表現為壓力越大，相對誤差越小的趨勢。綜上所述，所建立的有 限元分析模型合理可用。

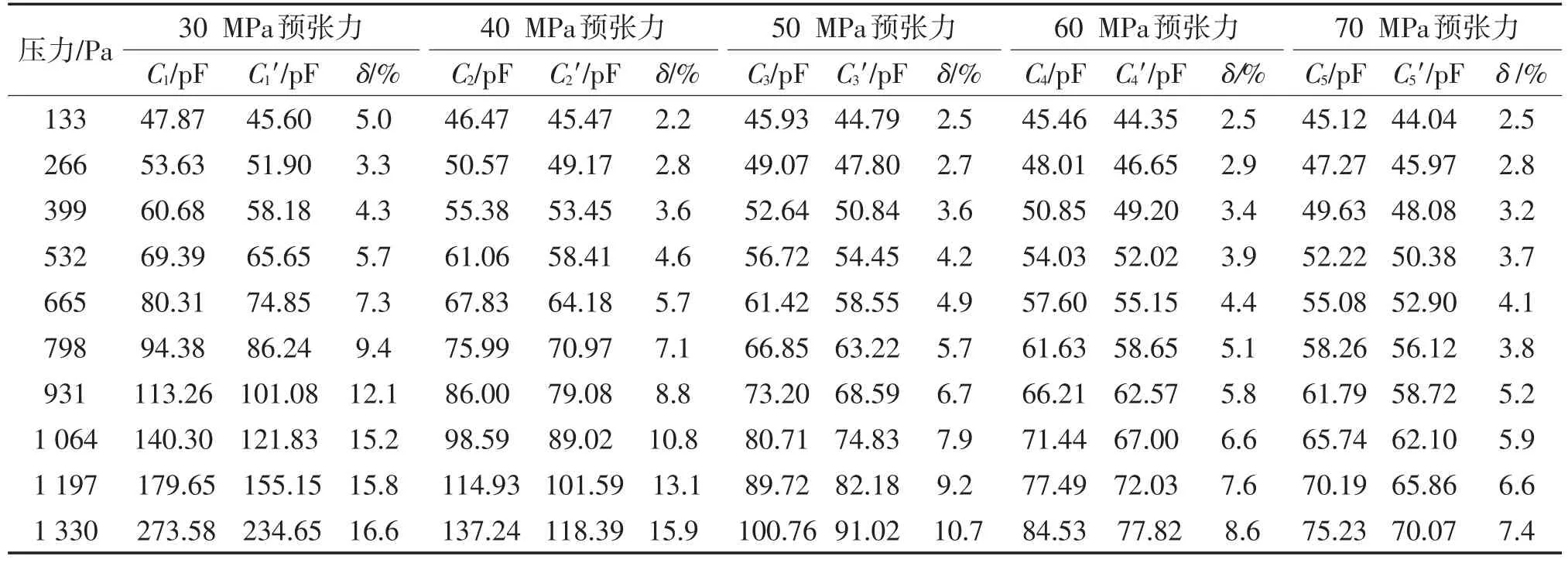
表2 不同預張力情況下輸出電容比較Tab.2 Comparison of output capacitance under different pretensions

圖3、圖4分別為不同預張力下感壓膜片中心撓度及輸出電容隨壓力的變化曲線。由圖3可知，感壓膜片中心撓度隨壓力呈非線性增大；預張力增大，中心撓度減小。

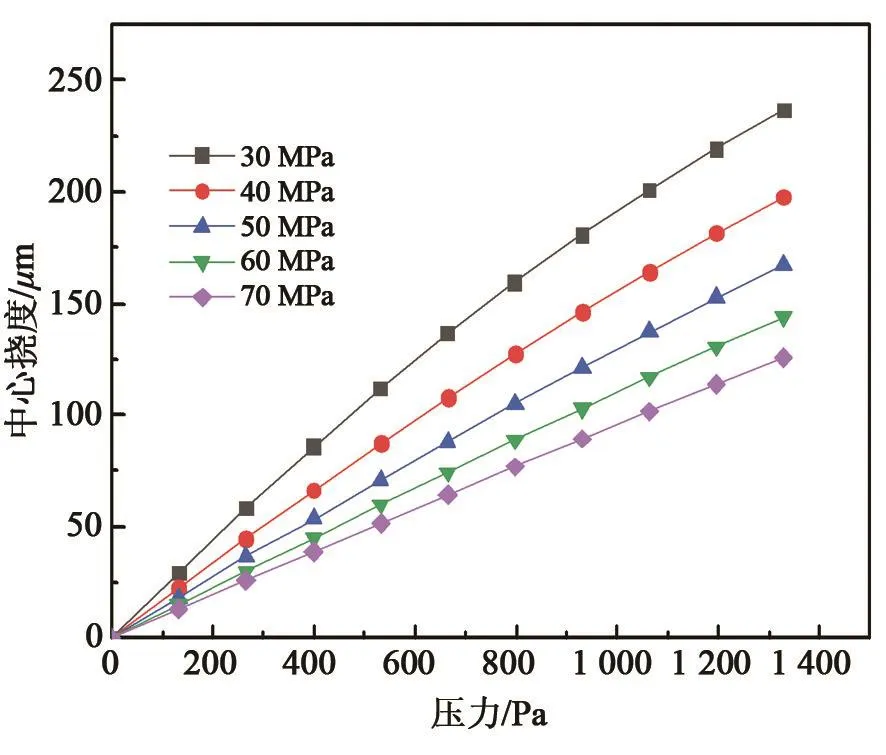
圖3 不同預張力下感壓膜片中心撓度隨壓力的變化曲線Fig.3 The curve of center deflection with pressure under different pretensions

由圖4可知，同一預張力下，隨待測壓力的增大，輸出電容增大。同一壓力下，增大預張力會導致輸出電容減小，減小幅度隨預張力的增大而逐漸降低。隨預張力的增大，輸出電容?壓力曲線逐漸趨于線性。壓力大于1 000 Pa時，單位壓力下輸出電容增量快速增大，特別當預張力為30 MPa時，增長最為明顯，這是由于等效電極距離減小、速度加快所致。在實際使用中，要盡量避免待測壓力值接近真空規量程上限。

圖4 不同預張力下輸出電容-壓力特性曲線Fig.4 Output capacitance-pressure characteristic curve under different pretensions

3.2 預張力對真空規性能的影響

真空規的性能評價指標主要有靈敏度、線性度、分辨率、遲滯差、重復性及穩定性等，預張力主要影響其線性度及靈敏度。真空規靈敏度的定義為，穩態工作下，輸出變化量與輸入變化量之比，用S表示。理想情況下，真空規的輸出特性曲線為一條直線，靈敏度是一個常數，但在實際過程中，輸出特性曲線并非直線，每點的靈敏度均不同。因此，在實際計算中，靈敏度可以用近似直線的斜率來表示，即S=ΔC∕Δp，ΔC為量程內輸出電容的變化量，Δp為待測壓力的變化量。采用最小二乘法分別對各預張力下的電容?壓力特性曲線進行擬合，擬合后得到的擬合直線與原特性曲線的電容最大偏差與滿量程輸出電容的百分比，即為真空規的線性度。不同預張力下真空規的靈敏度與線性度如表3所列。

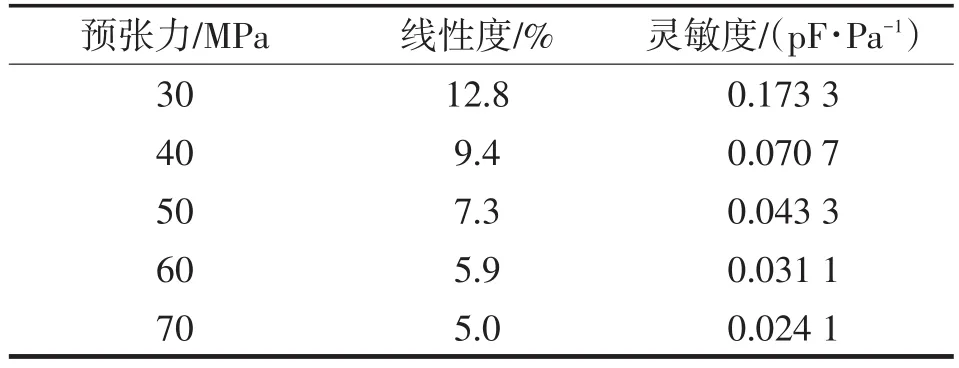
表3 不同預張力下電容薄膜真空規的線性度及靈敏度Tab.3 Linearity and sensitivity of capacitance diaphragm gauge under different pretensions

由表3可知，感壓膜片預張力增大，真空規的線性度提高，但靈敏度降低，故在真空規其他結構尺寸確定的情況下，必須準確控制薄膜預張力的大小，使其靈敏度與線性度均表現良好。預張力過大，會使真空規靈敏度變差，導致其對微小壓力的變化感知不靈敏，造成測量結果不準確；而預張力過小，會使真空規非線性誤差增大，穩定性變差，并增加后續信號處理及電測線路的設計難度。對于有限元模型，當預張力為50 MPa，氣壓在0～1 330 Pa內變化時，輸出電容的變化為42.88～100.76 pF，真空規的線性度為7.3%，靈敏度為0.0433 pF∕Pa，后續通過電路補償可進一步提高線性度。文獻[3]中設計了一種基于二極管橋的檢測電路，采用負反饋的方法，將非線性誤差從7.27%降低到0.662%。因此采用該種電路補償方法，當預張力為50 MPa時，可獲得較好的線性度與靈敏度。

為保證電容薄膜真空規能正常工作，必須考慮Inconel 600感壓膜片在量程內允許最大負載情況下的強度，因此通過COMSOL軟件計算膜片在受壓情況下的應力分布情況。圖5是預張力為70 MPa，氣壓為1 330 Pa下感壓膜片的應力分布情況。

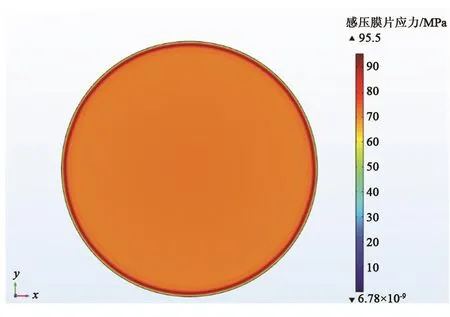
圖5 量程內允許最大負載情況下感壓膜片應力分布圖Fig.5 Stress distribution under the maximum load allowed in the range

圖5結果顯示，最大應力分布在薄膜邊緣，最大應力值為95.5 MPa，而Inconel 600合金的屈服強度為240 MPa，能夠滿足工作要求。

4 結論

本文以電容薄膜真空規電容感應模塊為研究對象，建立了預張力薄膜撓度及電容感應模塊輸出電容的理論模型，選用COMSOL軟件中特有的機電模塊進行了模擬仿真，得到不同預張力條件下，真空規輸出電容及感壓膜片中心撓度隨壓力的變化關系，仿真結果與理論結果基本相符，COMSOL軟件能對不同預張力薄膜的撓度及輸出電容進行有效分析，為后續薄膜的設計提供了參考。預張力對真空規的輸出特性影響明顯，預張力一定時，輸出電容隨待測壓力的增大而增大；隨預張力的增大，輸出電容減小，真空規的線性度提高，但靈敏度會隨之降低，可見電容薄膜真空規的線性度與靈敏度相矛盾。在后續設計安裝時，在滿足強度要求下，設計者必須合理控制感壓膜片預張力的大小，平衡線性度與靈敏度兩者的關系。