復合式高速直升機過渡走廊和最優過渡路線研究

朱漢，董睿，江順，盛守照

(南京航空航天大學 自動化學院，江蘇 南京 210016)

0 引言

復合式高速直升機既具備普通直升機的垂直起落、懸停、低空低速性能和良好的機動性等特點，又具備固定翼飛機的高速飛行能力，如圖1所示的美國某公司推出的復合式共軸雙旋翼高速直升機X2即為該構型的典型代表。

國內外主要針對復合式高速直升機氣動彈性耦合、建模分析和飛行控制等方面進行了研究，但很少見到有關復合式高速直升機過渡飛行方案、過渡走廊和過渡路線方面的研究分析。文獻[1]對復合式共軸直升機模型進行研究。文獻[2]進行了復合式共軸直升機3種飛行模式下的配平計算，但是沒有給出過渡過程的走廊曲線。文獻[3]采用線性過渡和功率最小優化過渡兩種過渡飛行方案對復合式共軸直升機過渡飛行過程的操縱策略進行了研究，也沒有給出走廊曲線。文獻[4]給出了一種傾轉三旋翼無人機過渡轉換的過渡策略，對過渡走廊曲線進行研究。文獻[5]研究了傾轉旋翼飛行器過渡走廊曲線的確定方法。文獻[6]針對傾轉旋翼飛行器在考慮約束的情況下，確定了發動機短艙傾轉角度-速度包線。文獻[7]針對傾轉旋翼機用最優控制方法研究傾轉旋翼機的最優動態傾轉過渡過程，得到對應的操縱策略和飛行軌跡。文獻[8]給出了一種傾轉旋翼機過渡段走廊曲線的設計方法。

圖1 X2高速直升機

本文針對復合式高速直升機在飛行模式轉換過程中所存在的過驅動問題，通過研究其過渡走廊，設計基于最大安全裕度的復合式高速直升機的最優過渡路線并優化過渡飛行方案。

1 建模分析

1.1 機體部件氣動模型

復合式高速直升機的主要部件包括一正一反旋轉的共軸雙旋翼、推進螺旋槳、機身(無機翼)、平尾(含升降舵)和垂尾(含方向舵)[9]，本文主要分析共軸雙旋翼以及推進螺旋槳的氣動模型。

1) 旋翼氣動模型

上、下旋翼縱向平面受力分析如圖2所示，其入流計算模型分別為：

(1)

(2)

式中：δ1和δ2為共軸雙旋翼的氣動干擾因子，由共軸雙旋翼干擾模型決定；v1和v2為共軸雙旋翼的平均誘導速度；K1和K2為共軸雙旋翼尾跡迎角的經驗函數，其表達式為：

(3)

(4)

上、下旋翼尾跡傾斜角χ1、χ2的表達式分別為：

(5)

(6)

式中：μ1、μ2分別為上、下旋翼的前進比；λ1、λ2分別為上、下旋翼的入流比。

平均誘導速度與拉力的關系由動量理論給出，表達式為：

(7)

(8)

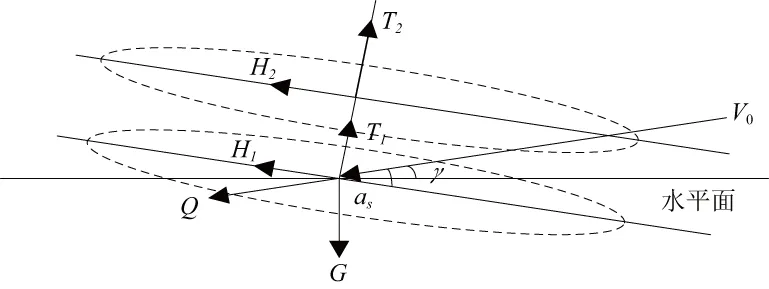
圖2 旋翼縱向平面受力分析圖

2)推進螺旋槳氣動模型

推進螺旋槳拉力和轉矩分別為：

(9)

式中：ρ為空氣密度；Rp為推進螺旋槳槳葉半徑；Ωp為推進旋翼轉速；Ctp為推尾拉力系數；Cqkp為推尾反轉矩系數。

1.2 整機全量動力學模型

將復合式高速直升機機身視為理想的剛體，定義直升機6個自由度分別為3個線速度Vx、Vy、Vz，3個角速度ωx、ωy、ωz。

可建立直升機的剛體運動方程組為：

(10)

繞質心轉動的動力學方程為：

(11)

直升機姿態角與角速率之間的運動學關系為：

(12)

式中：m是全機質量；g是重力加速度；Fx、Fy、Fz和Mx、My、Mz分別為雙旋翼、推進螺旋槳、機身、平尾和垂尾在復合式高速直升機質心處產生的氣動合力和合力矩；φ、θ、ψ分別是機體滾轉角、俯仰角和偏航角；Ixx、Iyy、Izz是機體質量對機體坐標系各軸的慣性積；Ixy是慣性積。

2 過渡走廊設計

2.1 飛行模式轉換及操縱遷移

復合式高速直升機有直升機和固定翼兩套操縱系統。兩套操縱系統的操縱效率在不同的前飛速度和飛行模式下有所不同：在懸停和低速前飛時，處于直升機模式；在中等速度前飛時，處于過渡模式；在高速飛行時，處于固定翼飛機模式。

直升機模式時需要負俯仰角使得高速直升機產生一個向前的分力，從而加速前飛；在固定翼飛機模式下，升力主要由主漿盤面與空氣相對運動所產生，此時希望保持平飛，使得主漿盤面可以產生足夠升力。過渡模式是由直升機模式到固定翼飛機模式(或由固定翼飛機模式到直升機模式)的必經過程，過渡過程僅僅作為一個暫時狀態，為簡化分析，主要研究其縱向運動。圖3為飛行模式轉換圖。

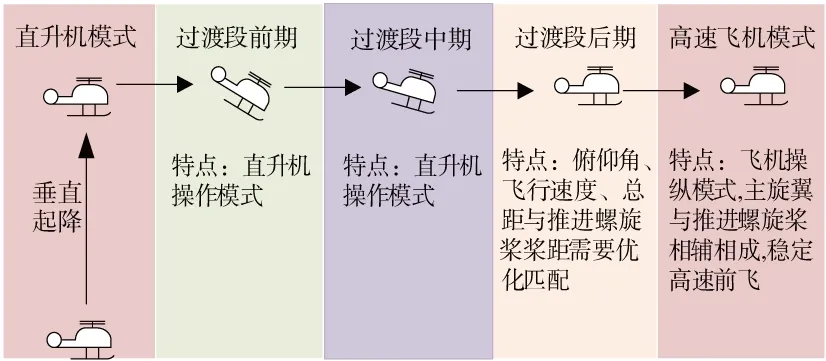
圖3 飛行模式轉換圖

表1所示為過渡模式的縱向操縱遷移過程，整個縱向過渡段分為全直升機模式、直升機主導的混合模式、固定翼主導的混合模式和全飛機模式。橫側向進入姿態保持模式，操縱保持滾轉平衡并跟蹤預定的(直線)過渡軌跡。

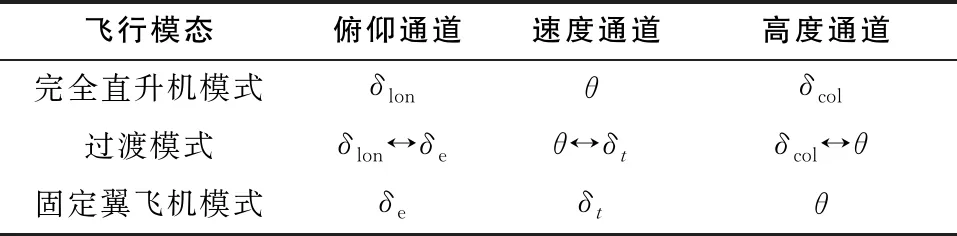
表1 過渡模式縱向操縱遷移

2.2 過渡走廊

過渡走廊[9]是直升機在任何時候都能夠安全過渡飛行的通道。考慮到復合式高速直升機橫側向在過渡段進入姿態保持模式，而高度通道也進入保持模式，其過渡走廊主要由飛行速度、俯仰角、推進螺旋槳變距、縱向周期變距、升降舵和總距等組成，其中飛行速度和俯仰角對(V,θ)是獨立的，推進螺旋槳變距、縱向周期變距、升降舵和總距是非獨立的，推進螺旋槳變距主要用于飛行速度控制，縱向周期變距和升降舵用于俯仰姿態控制，總距用于保持高度控制。

基于過渡走廊的定義，直升機過渡飛行過程中，需要對直升機飛行速度和俯仰角加以分析：當俯仰角保持不變，若飛行速度過小，機身、平尾以及主漿盤面產生的升力不足以平衡重力；若飛行速度過大，導致主旋翼后行槳葉失速和前行槳葉激波，則主旋翼產生的升力不足以平衡直升機自身的重力。

對高速直升機的俯仰角變化做出規定以便建立安全的過渡走廊。本文規定：過渡飛行狀態下復合式高速直升機的俯仰角小于失速俯仰角；鄰近狀態下的俯仰角變化小于一定范圍，即

(13)

采用狀態點分析的方法來確定高速直升機的安全過渡走廊。通過對模型進行分析，可以得到不同飛行速度和俯仰角時，高速直升機對應的狀態量，結合上述規定可以得到復合式高速直升機的過渡飛行走廊(圖4)。

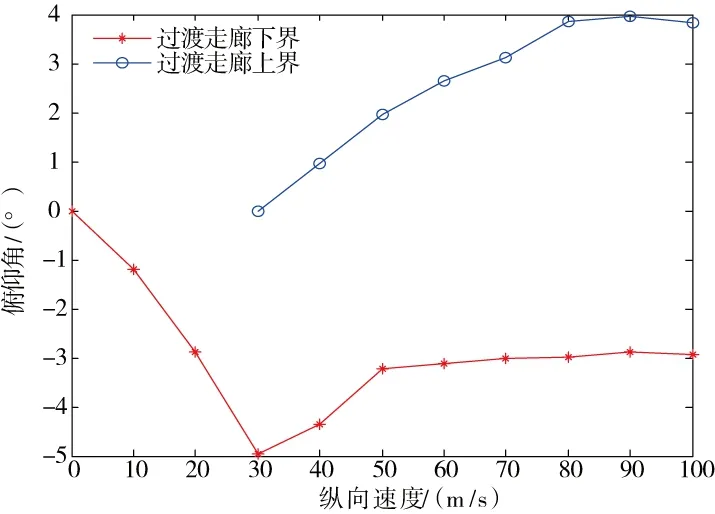
圖4 過渡飛行走廊

理論上，得到高速直升機過渡走廊后，可以在過渡走廊范圍內繪出無數條不同的飛行模式轉換軌跡。

3 最優過渡路線設計

3.1 最優目標選擇

在確定復合式高速直升機過渡走廊以后，需要在過渡走廊范圍內選擇一條最優的飛行模式轉換軌跡。考慮到復合式高速直升機過渡過程最重要的是安全保障，因此本研究將優化目標設定為過渡走廊的最大安全裕度。這樣復合式高速直升機在過渡段具有足夠的安全范圍，提高過渡過程的可靠性。

(14)

(15)

(16)

(17)

(18)

定義安全指標函數

(19)

優化目標為安全裕度最大，即目標函數

J=maxf(V,θ,δe,δlon,δt,δcol)

(20)

3.2 基于粒子群算法的最優過渡路線

采用粒子群優化算法[10]確定復合式高速直升機在過渡過程中的配平值，即以優化值作為配平方程組的唯一解，以此來解決操縱冗余問題。

粒子群優化算法將解非線性方程組的數值解問題轉化為極大優化問題,以式(20)作為粒子的適應度評價函數。粒子群優化初始化為一組配平狀態點,然后通過迭代得到最優解。粒子通過跟蹤兩個極值在迭代中更新自己。

粒子群優化的迭代公式為

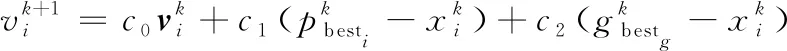
(21)

(22)

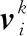
粒子群優化算法主要計算步驟如下：

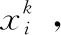
2) 計算粒子的適應度值J；

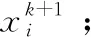
5) 檢查結束條件：所有粒子的最優值小于給定誤差ε，滿足條件即結束尋優；不滿足，則跳轉至2)且k=k+1。

過渡段優化配平流程圖如圖5所示。

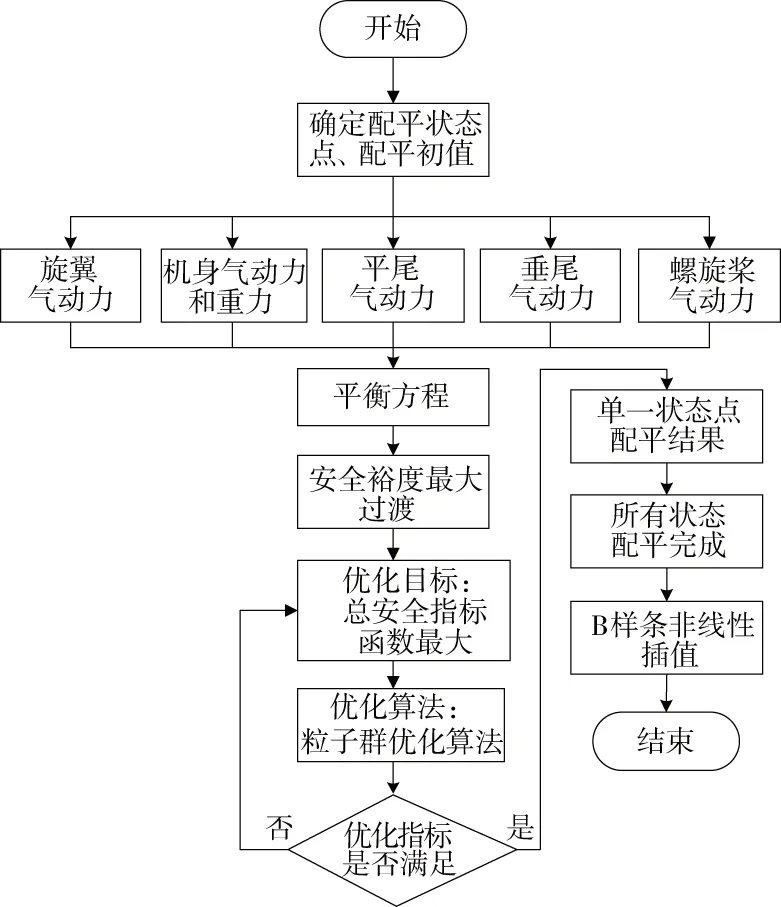
圖5 過渡段優化配平流程圖

4 仿真驗證

最優過渡路線是基于過渡走廊和安全裕度最大確定的一條過渡路線。最優過渡路線規劃模塊輸入為直升機的飛行速度、高度、垂向速度和俯仰角，輸出為8個執行機構(全動平尾、橫向周期變距、縱向周期變距、推進式螺旋槳、差動平尾、差動總距、方向舵、俯仰角和全動總距)的配平量和俯仰角的配平量。

以美國某公司研制的時速高達259英里(約合417 km/h)的復合式共軸剛性雙旋翼高速直升機為例，基本參數如表2-表4所示。

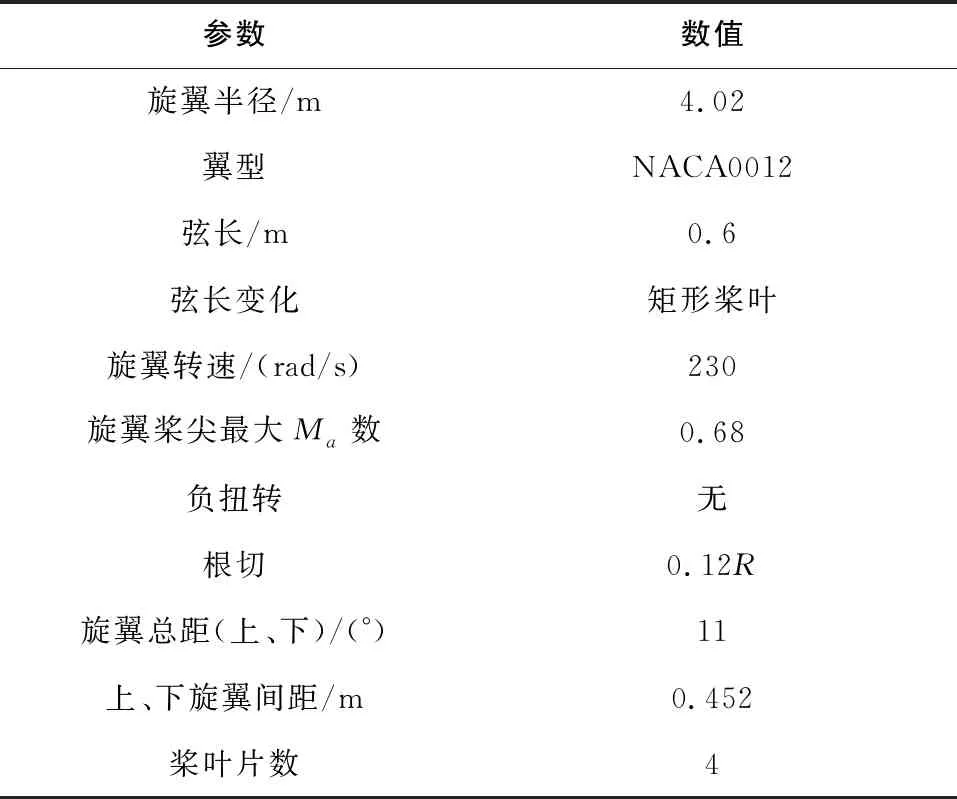
表2 復合式高速直升機旋翼基本參數

表3 復合式高速直升機機身幾何參數

表4 復合式高速直升機整機參數

仿真得到過渡段的最優過渡路線以及操縱和姿態對速度的變化規律，如圖6-圖8所示。

以直升機模式向飛機模式轉換為例，圖6為最優過渡路線，圖7和圖8為過渡飛行模態下縱向通道操縱量隨著速度增加的變化趨勢。當飛行速度較低時，復合式高速直升機處于直升機模式，產生負俯仰角低頭前飛，此時俯仰姿態是由縱向周期變距δlon控制，速度由俯仰角θ控制，并通過控制總距δcol實現高度保持。當飛行速度達到過渡起點速度時，升降舵δe具有一定的舵效，此時縱向周期變距δlon逐步改出，升降舵δe隨著飛行速度的增加不斷改入；同時在速度控制回路加入尾推螺旋槳距δt控制，高度保持依然通過控制總距δcol實現。當俯仰角θ達到縱向模式切換點后，俯仰角θ參與到高度控制，并完全退出速度控制回路，此時總距δcol逐步改出，直到過渡完畢高度控制全部通過控制俯仰角θ實現。

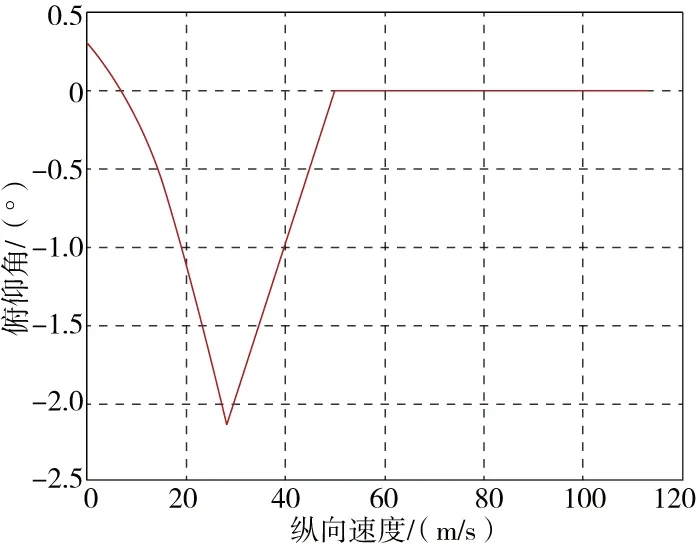
圖6 最優過渡路線

圖7 縱向周期變距δlon和升降舵δe對速度的變化規律

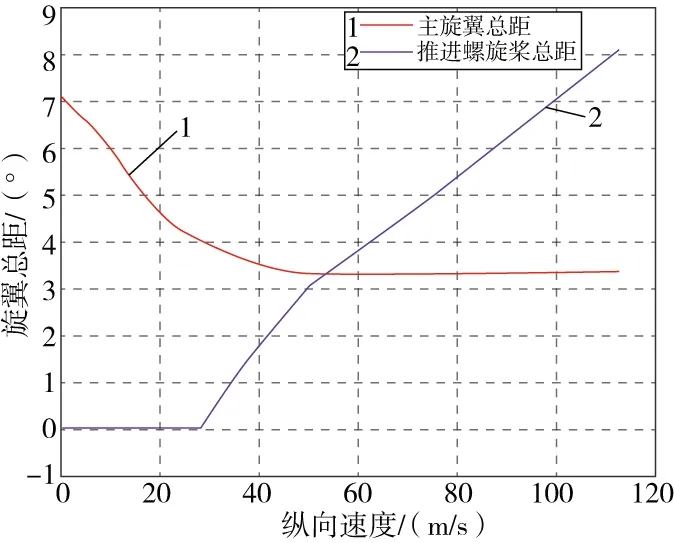
圖8 總距δcol和推進螺旋槳總距δt對速度的變化規律

5 結語

復合式高速直升機從直升機模式轉換到固定翼飛機模式的過程中，存在操縱冗余和升力匹配問題，導致過渡過程的操縱分配相當復雜。本研究對高速直升機進行了過渡模式下的配平，獲得約束條件下的過渡走廊，采用安全裕度最大優化過渡路線，得到了過渡飛行過程中操縱和姿態對速度的變化規律。仿真結果表明：最優過渡路線能確保高速直升機在飛行模式轉換過程中合理地分配各操縱量；有效解決了操縱冗余問題，并確保了模式轉換的安全性。