綠色發展理念下中國能源消費與碳排放的預測分析

郝園園

摘 要：自1990年以來，世界各國開始重視全球氣候及能源在經濟發展中的作用、追求低碳經濟發展以及有效利用能源和減少環境污染的模式。改革開放加快了中國工業化生產和城市化發展進程，致使能源總消耗的需求量急劇增加，并且能源消耗產生的碳排放量不斷增加。“十三五”規劃提出了綠色發展理念，綠色經濟是在經濟高速發展過程中實現能源的低消耗、能源效率的高轉化以及與環境和諧共處的發展模式。所以在保持經濟高速增長的同時，勵志于改變國民生產和生活方式，提高綠色低碳水平，有效控制碳排放總量，也是中國未來發展過程中一項具有約束力的目標。低碳經濟是必要性、可行性的，是實現經濟長久健康發展的必要途徑，也是推動社會文明建設的必然選擇。為了預測中國經濟發展中的能源消耗和碳排放，GM（1，1）預測模型主要用于預測能源消耗和碳排放的未來發展趨勢，對于改善能源消耗和碳排放具有一定的參考意義。

關鍵詞：能源消費;碳排放;GM（1，1）預測模型;能源資源;煤炭資源

中圖分類號：F206 文獻標識碼：A 文章編號：2096-0298（2021）01（b）--03

能源資源是社會經濟發展的動力中樞，是國民生活、生產與發展的物質基礎保障。回顧歷史，能源的發展離不開社會的進步與發展，反之經濟發展是以能源資源為核心，能源也是以經濟發展為基礎保障。自20世紀80年代以來，我國的經濟不斷加速發展，能源消費量也隨之增加。目前我國的一次能源結構主要以煤炭為主，雖然近年來風電、光伏、核能等可再生能源快速發展，對天然氣的利用也有所增加，但從能源消費情況和能源消費結構上看，煤炭資源消費仍占據主導地位。在能源消費結構中，煤炭消費總量占一次能源消費總量的比例一直居高不下，平均比重占70%;其他能源僅占能源總消費的30%。以2018年為例，2018年煤炭能源消費總量約27.38億噸標準煤，占能源總消費約59%，同比增長0.96%。隨著我國石油、天然氣、水電核產業的不斷發展，對傳統資源的消費有所減緩。天然氣消費總量約3.62億噸標準煤，占能源消費總量的6.77%，同比增長15.15%。石油消費量8.77億噸標準煤，占能源總消費的3.9%，同比增長3.89%。風電核能源消費約6.64億噸標準煤，占消費總量的14.3%，同比增長7.08%。由此可見，煤炭能源在我國能源消費結構中占有絕對主導地位，這也是導致溫室氣體（二氧化碳）持續增加的一個主要原因。然而在其他能源中，尤其是風、電、水和核能等綠色清潔能源的二氧化碳排放幾乎為零，但在我國的一次能源消費結構中占比不到10%。由此看來，在未來研究工作中，優化能源產業結構，能源消費方式的多元化以及提高能源效率將成為我國減少二氧化碳排放與實現綠色可持續發展道路的主導方向。此外，近年來我國風、電、水和核能等綠色清潔能源的比重呈緩慢增長的趨勢。截至2018年，綠色清潔能源由1975年的4.6%增長到了14.3%。可見，我國已經意識到能源結構與消費方式的不合理問題，開始逐步優化能源相關產業結構代替傳統產業，進一步實現低碳、綠色可持續發展的戰略方針，同時也為進一步實現環境與社會經濟發展共存模式奠定基礎，實現能源消費多元化。黨的十九大以來，我國一直提倡能源產業低碳、綠色、健康、可持續發展的戰略，堅持能源節能減排、低碳綠色發展與環境共存和諧發展方針。同時努力實現能源產業結構升級和優化能源產業結構，降低能耗與提高能源的使用效率，未來在能源綠色可持續發展的道路上將面臨嚴峻的挑戰，其對于眾多學者而言這也成為更具有意義的研究性課題。本文通過建立灰色GM（1，1）預測模型基于1975—2018年國家統計局數據，對我國能源消費和碳排放為指標變量進行分析預測。

1 灰色GM（1，1）預測模型理論

灰色預測主要是通過系統模型對確定性信息和不確定性信息進行系統性預測，也就是數據變量在一定周期內變動狀況與時間相關的灰色過程以及針對數據變動軌跡和趨勢的相似度進行分析預測。所以灰色預測GM（1，1）模型如下：

GM（1，1）預測模型的精度主要是通過模型的相對誤差P和均方差比值C進行檢驗。如果預測值與原數列精度越高，表明模型的擬合度就越好，如表1所示。

2 非線性GM（1，1）預測模型理論

在經濟發展過程中，能源消費和碳排放之間是否存在線性與非線性的關系，對其影響因素較為復雜。非線性GM（1，1）模型預測是基于灰色系統預測的數據處理后再次預測，是對數據誤差修正的判斷，對數據的預測具備可控性。通過GM（1，1）模型不斷得出新的預測值、新的殘差序列值，計算出一個新的參數，建立新的動態關系。所以預測數據與原始數據變化基本一致，具有良好的精準程度。非線性GM（1，1）模型是以經典GM（1，1）模型為基礎，基于原始數據x（0）（k）與x（0）（k）的線性關系的假設。若x（0）（k）與x（1）（k）不滿足線性關系的條件，那么非線性GM（1，1）模型對數據擬合度的預測更佳。即建立非線性GM（1，1）模型如下：

3 回歸預測模型

回歸預測分析主要是通過最小二乘法利用歷史數據之間的因果關系建立回歸模型進行預測。該方法適用于變量單一、影響因素簡單化，并且預測精度高、使用方便、對數據可進行長期預測等特點。回歸分析預測法包括一元線性回歸預測法、多元線性回歸預測法和非線性回歸預測法等。在實際數據分析中，影響預測變量的因素存在多個，那么就要通過多元進行回歸分析。在多元回歸分析中大多數非線性回歸都可轉化為線性回歸來實現，其多元線性回歸分析的原理與一元線性回歸分析原理完全相同。

4 GM（1，1）模型預測檢驗

4.1 能源消費GM（1，1）預測模型

在GM（1， 1）預測模型中，如果能源消費這一變量在一定周期內的變化趨勢與時間相關，所以能源消費GM（1， 1）模型如下：

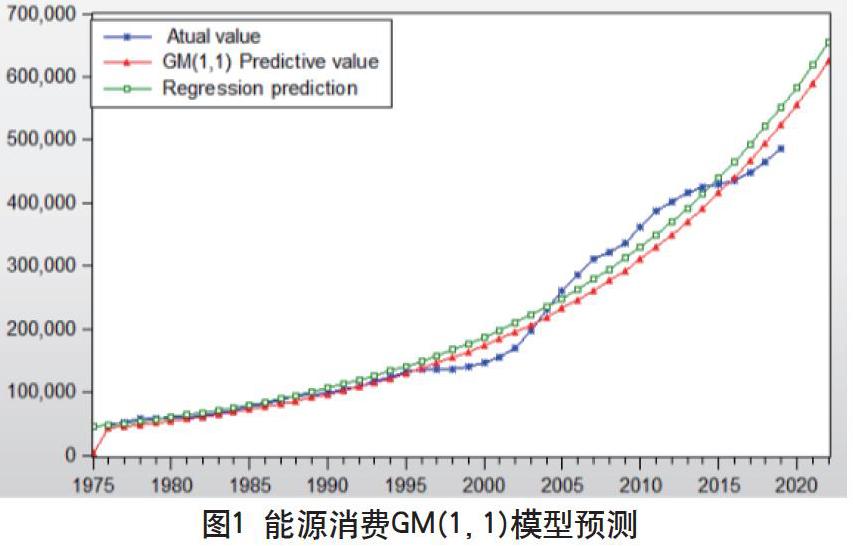
根據式（13）計算可知，能源消費GM（1，1）模型的精準度為P= 92.28% > 90%，所以GM（1，1）模型合格。由圖1可知，利用GM（1，1）模型與回歸預測模型的能源消費量預測值的走勢和真實值的走勢基本一致。GM（1，1）模型與回歸預測模型相比，GM（1，1）模型更加準確存在誤差較小。雖然預測結果都存在一定的誤差，但對能源產業發展趨勢具有一定的參考意義。2018年我國能源總消費464000萬噸標準煤，隨著我國的經濟不斷發展，未來我國能源總消費量將持續增長。如果中國的能源總消費和需求因素在未來四年內不發生重大變化，到2022年中國的能源消費總量將有可能增長至587415萬噸標準煤，預計比2018年可能增長26.6%左右。

4.2 碳排放GM（1，1）預測模型

本節基于中國國家統計年鑒1975—2018年的碳排放數據，建立單一灰色GM（1，1）預測模型利用線性回歸與統計方法相結合對能源消費進行預測。則碳排放GM（1，1）模型的時間響應序列如下：

根據式（13）計算可知，碳排放GM（1，1）模型的精準度為P= 88.5% > 80%，所以GM（1，1）模型合格。所以由圖2可知，利用GM（1，1）模型與回歸預測模型的碳排放量預測值的走勢和真實值的走勢基本一致。結合GM（1，1）預測模型和回歸預測模型預測結果可知，隨著經濟不斷的發展，二氧化碳的排放量不斷增加，后期也存在上升的趨勢，對環境與經濟的協調發展帶來巨大的考驗。2018年我國碳排放總量超過101.45億噸，在未來隨著工業化經濟不斷發展，我國碳排放總量將有可能持續增長，如果中國的能源消費、人口等影響因素在未來四年內不發生重大變化，到2022年中國的能源消費總量將有可能增長至121.33億噸左右，預計比2018年可能會增長19.5%左右。

通過灰色GM（1， 1）預測模型與回歸預測模型對歷史數據的預測分析，兩種預測方法對我國能源消費量和碳排放的預測結果是有差距的，用回歸預測模型所得的預測值大于GM（1，1）預測模型，更接近實際值。GM（1，1）預測模型對能源消費和碳排放的影響程度較大的因素充分考慮在模型中，通過已知變量來預測未來的趨勢更具有解釋性和理解性。

5 結語

本文基于經濟發展數據對中國的能源消費總量以及碳排放總量進行了預測。對于中國能源消費總量和碳排放總量的預測，首先使用了灰色GM（1，1）模型，其次將對能源消費總量和碳排放總量具有重要影響因素考慮在內建立了回歸預測模型，最后建立了中國能源消費的回歸模型，預測了基準情景和低碳情景下中國2020—2022年的能源消費量以及碳排放量。因此，對于我國政府而言，在產業結構升級和宏觀調控中起著至關重要的作用。第一，應加強政府對相關產業的干預與指導，制定綠色低碳可持續發展相關的政策體系，例如通過減稅、風險補償和專項資金等優惠政策鼓勵中小企業進行產業結構優化與升級;第二，以完善健全碳排放交易市場和溫室氣體（二氧化碳）排放標準體系為目標，實行嚴格考核與問責制，促進綠色低碳技術推廣與投入;第三，要建立健全的處罰制度，對工業企業進行定期監督檢查，規范節能減排標準制度與執行力度，大力發展綠色節能環保產業，促進社會經濟與環境的綠色協調可持續發展。

參考文獻

謝凱，南靈.基于STIRPAT模型的陜西省建設用地對能源消費碳排放的影響[J].湖北農業科學，2016（03）：599-602.

榮蓉.山東省工業碳排放情景預測及減排策略研究[J].中外能源，2016（02）：94-100.

趙選民，段曉琛.基于STIRPAT模型的陜西省碳排放影響因素分析[J].財會月刊，2016（12）：31-34.

嫣嫣，李爽，夏青.中國居民生活用能碳排放影響因素分析——基于STIRPAT模型[J].生態經濟，2017（05）：42-47.

武紅，谷樹忠，周洪.河北省能源消費、碳排放與經濟增長的關系[J].資源科學.2011，33（10）：1897-1905.

馮思靜，鄧元月，馬云東，等.中國能源消費預測灰色建模法[J].數學的實踐與認識，2012，42（03）：78-84.

巧張勇，劉嬋，姚亞平.GM（1，N）與GM（0，N）模型在能源消費碳排放預測中的比較研究[J].數學的實踐與認識，2014，44（05）：72-79.

賴紅松.基于灰色預測和神經網絡的人口預測[J].經濟地理，2004，24（02）：197-201.