淺談小學數學課堂教學如何為初中教學埋好“伏筆”

曹前文

摘要：盡管幾何、方程、集合、概率等內容在小學高年級數學教材中都有所涉及，可多數小學生進入初中學習后，似乎都要經歷一段“不適期”“迷茫期”，甚至覺得有道過不去的“坎”。其實，學科知識的學習都是循序漸進、漸入佳境的過程。若在小學數學學習階段，教師科學合理地為初中數學學習埋好“伏筆”，就能有效地避免這種現象的發生，從而讓孩子們一以貫之、與時俱進地樂學數學，學好數學。

關鍵詞：

小學?數學?課堂教學?初中?伏筆

現在的數學體系分為四大領域，即數與代數、空間與圖形、統計與概率、實踐與綜合運用。這些數學內容貫穿整個義務教育階段，只是各個學段的目的、任務和要求不同，所采取的教學手段和學習方法存在差異，這就容易導致孩子在小學階段數學學得相當好，到了中學后卻優勢不再，甚至出現了“七年級勉強適應，八年級就此分化”的現象。當然，這也不排除有智力等因素的影響。學科知識學習都是由淺入深、由易漸難、環環相扣的。筆者結合自身工作實踐，就如何在小學數學課堂教學中為中學數學學習埋好“伏筆”、做好銜接，做了一些探索和思考，以期得到廣大同仁指教。

一、力抓規范解答，培養學生思維的縝密性，為后續的幾何證明學習埋好“伏筆”

小學生解題大多憑直覺，喜歡死盯著題目看，“袖手旁觀”，不打草稿。可孩子的思維往往比較直觀且有限，光“動腦”不“動手”，不僅學習效率大打折扣，還往往顧此失彼、丟三落四。而幾何圖形的學習，對思維的縝密性有相當高的要求，在思考問題時必須“步步為營”，切不可“天馬行空”。學生必須清楚每種圖形之間的內在聯系及有關計算公式的推導過程。因此，在課堂教學中，教師應緊扣圖形，先出示字母公式，再代入數字計算。在練習中也應要求學生這樣做，久而久之，孩子們就會養成規范解答的習慣。遇到稍微復雜的問題時，用公式推理，解題就會簡單很多。平面圖形的周長與面積的計算，立體圖形的表面積、體積的計算，相交與平行，點、線、面、體的關系等，這些都是幾何學最基本的知識，其重要性不言而喻，學生一定要爛熟于心。若煮成“夾生飯”，出錯便避免不了。例如，在計算圓錐的體積時，學生都知道圓錐的體積是與它等底等高的圓柱體積的1/3。可是在實際計算時，學生經常忘了乘13，直接用底面積乘高。還有像三角形、梯形面積的計算，經常忘了乘1/2等。

小學生的思維特點是以具體形象為主，通過觀察和思考得出答案，但是不能用文字和公式把每一步的思考過程有條理地表示出來，而初中數學講究的是得出此結論的步驟和過程，每一步的推導都要有理有據。這顯然是相矛盾的，無疑為課堂教學的主導者——授課教師的主觀能動性的有效發揮提供了廣闊的空間。因為在課堂教學中，對于學生的規范解答一定要抓緊抓實、久久為功，讓其形成良好的習慣。

二、講清弄透每一個數學問題的推理過程，在判斷推理中為中學數學學習埋好“伏筆”

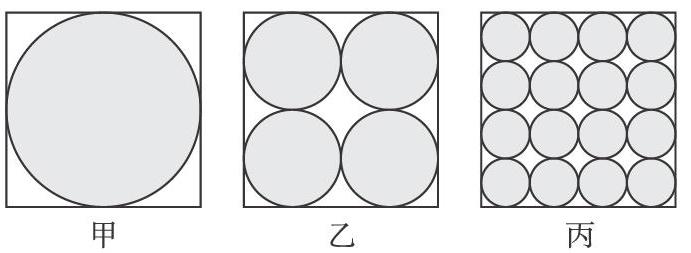
小學數學重具體形象，中學數學重邏輯推理，兩者看似矛盾，實為對立統一。教師在平時的教學過程中要有意識地點撥、滲透。例如，小學數學總復習中有這樣一道題：從三張邊長是7厘米的正方形鐵皮中分割出不同規格的圓片，剩下的廢料（?）。

A.甲最多

B.乙最多

C.丙最多

D.甲、乙、丙同樣多

甲方法是從正方形鐵皮中分割出一個最大的內切圓，乙方法是把正方形鐵皮4等分后分割出的4個內切圓，丙方法是把正方形鐵皮16等分后分割出的16個內切圓。

學生首先是從直觀上來判斷，可是在判斷的過程中很容易迷惑：甲方法中圓的面積大，所以剩下的廢料少;乙和丙方法中雖然圓的個數比較多，但面積小。所以輕易下了錯誤結論。而稍微細心的學生感覺到不對，就想到了具體計算。這道題的關鍵是找到圓的半徑，甲方法中圓的半徑為7÷2=3.5（cm），乙方法中每個圓的半徑是3.5÷2=1.75（cm），丙方法中每個圓的半徑是1.75÷2=0.875（cm）。若直接計算，則運算量特別大，且耗時長并容易出錯。這時候用字母來幫忙推理，就可以清晰地把自己的思考過程呈現出來，化繁為簡，而這在中學階段往往是最常用的解題方法。可以假設正方形的邊長為d，則甲方法中圓的半徑是d/2，乙方法中每個圓的半徑是d/4，丙方法中每個圓的半徑是d/8。這時讓學生歸納推理就不難得出：雖然圓的個數與圓的半徑都不相同，但是由于正方形鐵皮的邊長不變，因此圓的總面積不變，剩下的面積也就相等了。這樣由具體計算到用字母說理，無形中培養了學生的判斷推理能力和符號化思想，顯然為中學學習定律、公理的推導埋好了“伏筆”。

圓面積的計算方法推理，圓柱、圓錐體積計算方法的推理，長方形、正方形、三角形、梯形面積的計算公式的由來，以及它們之間的聯系等內容，其推理過程都應讓學生熟練掌握。

三、注重培養學生的數學思想方法，為后續的數學學習解題能力的提升埋好“伏筆”

小學數學中有很多的數學思想方法，如低年級的數數，有“正”著數——從小到大，“倒”著數——從大到小。隨后，要求學生先找規律，再接著往下數。這是函數思想在小學數學學習中的萌芽狀態，隨著后續的學習，像圖形的周長、面積公式與體積公式，解決問題中數量之間的關系——單價、數量與總價，速度、時間與路程，工作效率、工作時間與工作總量，五年級學習的折線統計圖，以及六年級學習的正比例關系和反比例關系中兩種相關聯的量中蘊含的變化規律等，均為函數思想的呈現。而函數在中學階段是重點也是難點，特別是函數圖像，實際上在小學階段也有涉及，如《數學好玩》章節中的看圖找關系，即與中學的函數圖像有著密切聯系，在教學過程中可以適當多做鋪墊、多搭橋、多引導。

正比例的圖像是一條直線，而小學階段的正比例圖像呈現的是直線的一部分，反比例圖像在小學六年級下冊中作為課外閱讀“你知道嗎？”出現。這些知識不能一帶而過，可以以符合小學生具體形象思維為主的思維方式列舉出一組數據，形成表格，畫出圖像，讓學生經歷畫圖像的過程，通過觀察比較，得出正比例函數圖像是一條直線，而反比例函數圖像是一條曲線，并且曲線的兩端分別向橫軸和縱軸逐漸靠攏，這同時又體現了極限思想方法。描點的過程中，直線上的點（數軸）與表示具體的數是一一對應的，并且孕育著函數思想。在分數應用的教學中，經常要用到轉化的數學思想方法來解決問題，這樣可以培養學生思維的靈活性。