空間向量應用的誤區提醒

■山東省單縣第一中學 王慶敏

空間向量是解答立體幾何問題的有力工具，問題求解的過程是通過建立空間直角坐標系，引入點的坐標，表示出相關向量，將距離、平行、垂直、夾角問題轉化為相應的向量關系問題。但同學們在應用空間向量解題時，常會由于建系不合理、混淆有關概念、過程不規范等原因，造成錯誤。本文總結了幾類典型的易錯點，給予提醒。

一、建系不合理或盲目建系

建立空間直角坐標系是應用空間向量解題的“起點”，通過恰當建系、準確求出點的坐標，再表示出相應向量，進而利用向量的關系求解空間幾何問題。但要注意的是解題時要避免盲目建系，小題大做（證明平行、垂直一般不需要建系；求解距離時很少建系；在易作平行線求異面直線所成的角、易作平面的垂線求線面角、易作交線的垂線求二面角時可不用建系）。

例1（吉林長春2020屆高三質量監測（三））如圖1所示，在四棱錐P-ABCD 中，底面ABCD 為直角梯形，BC∥AD，AD⊥DC，BC=CD=1，AD=2，PA=PD，E 為PC 的中點，平面PAD ⊥平面ABCD，F 為AD 上一點，PA∥平面BEF。

（1）求證：平面BEF⊥平面PAD；

（2）若PC 與底面ABCD 所成的角為60°，求二面角E-BF-A 的余弦值。

解析：（1）如圖1，連接AC 交BF 于G，連接EG，因為PA∥平面BEF，PA ?平面PAC，平面PAC∩平面BEF=EG，所以PA∥EG。

又E 為PC 的中點，所以G 為AC 的中點，由△AFG≌△CBG，可得AF=BC=1=，所以F 為AD 的中點。

圖1

因為BC∥FD，且BC=FD，所以四邊形DCBF 為平行四邊形。

因為AD⊥DC，所以BF⊥AD。

又BF?平面ABCD，已知平面PAD⊥平面ABCD，平面PAD ∩平面ABCD =AD，故BF⊥平面PAD。

又BF?平面BEF，所以平面BEF⊥平面PAD。

（2）連接PF，因為PA=PD，F 為AD的中點，所以PF⊥AD。

又PF?平面PAD，平面PAD ⊥平面ABCD，平面PAD∩平面ABCD=AD，所以PF⊥底面ABCD。

又BF⊥AD，所以以F 為坐標原點，FA，FB，FP 所在直線為x 軸，y 軸，z軸，建立如圖2 所示的空間直角坐標系F-xyz。

設P（0，0，t），C（-1，1，0），取平面ABCD 的法向量為n1=（0，0，1）。

圖2

設平面EBF 的法向量為n2=（x，y，z），則

誤區提示：恰當建立坐標系是使計算簡捷的有力保障，如果建系不合理，會導致點的坐標無法求出或不易求得，向量無法表示，進而使計算過程較為煩瑣，甚至可能出現無法計算出結果的情況。解答本題時，同學們的建系方式五花八門，有一部分同學把點B 或D 視為空間直角坐標系的坐標原點，導致某些點的坐標不易求解，陷入解題誤區。

二、過程不嚴謹

建立空間直角坐標系時，要選擇兩兩垂直的三條直線為坐標軸，但這種垂直關系往往不會直接給出，而是需要先證明后再應用。

例2（2020 年 江 蘇徐州高三月考）如圖3，在四棱錐E-ABCD 中，底面ABCD 是圓內接四邊形，CB=CD=CE=1，AB=AD=AE =，EC⊥BD。

圖3

（1）求證：平面BED⊥平面ABCD；

（2）若點P 在平面ABE 內運動，且DP∥平面BEC，求直線DP 與平面ABE 所成角的正弦值的最大值。

解析：（1）如圖3，連接AC，交BD 于點O，連接EO。

因為AD=AB，CD=CB，AC=AC，所以△ADC≌△ABC，易得△ADO≌△ABO，所以∠AOD=∠AOB=90°，所以AC⊥BD。

又EC⊥BD，EC∩AC=C，所以BD⊥平面AEC。

又EO?平面AEC，所以OE⊥BD。

又底面ABCD 是圓內接四邊形，所以∠ADC=∠ABC=90°，在Rt△ADC 中，由AD =，CD=1，可得所以易得△AEO∽△ACE，所以∠AOE=∠AEC=90°，即EO⊥AC。

又AC，BD ?平面ABCD，AC∩BD=O，所以EO⊥平面ABCD。

又EO?平面BED，所以平面BED⊥平面ABCD。

（2）如圖4，取AE 的中點為M，AB 的中點為N，連接MN，ND，DM，則MN∥BE。

由（1）知∠DAC=∠BAC=30°，即∠DAB=60°，所以△ABD 為正三角形，所以DN⊥AB。

又BC⊥AB，所以DN ∥BC，所以平面DMN∥平面EBC，所以點P 在線段MN 上。

以O 為坐標原點，建立如圖4所示的空間直角坐標系O-xyz，則

圖4

誤區提示：空間直角坐標系的建立要充分利用題目中直接或間接給出的線線垂直關系，本題中給出了矩形、等腰三角形，因此可利用相關圖形的性質得到線線垂直關系。類似地，若題目條件中含有菱形，則可利用其對角線互相垂直得到線線垂直關系。但要注意，在問題的求解中利用這些關系建立坐標系時，要給出必要的說明。

三、忽視線面角與向量角的關系

線面角是直線與其在平面內的投影的夾角，而利用空間向量求線面角時，通常求出的是直線的方向向量與平面法向量的夾角，要注意二者的關系。

例3（2020年貴州遵義高三期中（理））如圖5，正方形AMDE 的邊長 為2，B，C 分別為邊AM，MD 的中點，在五棱錐P-ABCDE 中，F 為 棱PE 的中點，平面ABF 與棱PD，PC 分別交于點G，H。

（1）求證：AB∥FG；

（2）若PA ⊥底 面ABCDE，且PA=AE，求直線BC 與平面ABF 所成角的大小。

解析：（1）在正方形AMDE 中，因為B是AM 的中點，所以AB∥DE。

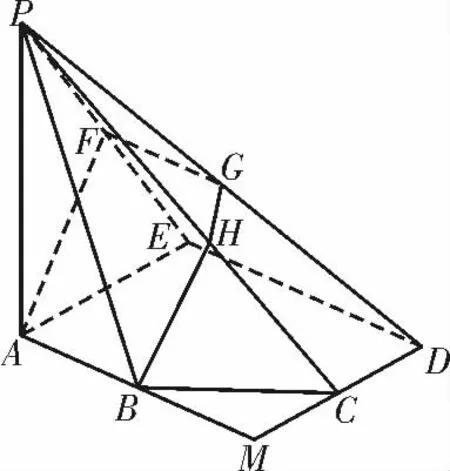
圖5

（2）因為PA ⊥底 面ABCDE，所以PA⊥AB，PA⊥AE，如圖6，建立空間直角坐標系A-xyz，則 A（0，0，0），B（1，0，0），C（2，1，0），P（0，0，2），F（0，1，1）=（1，1，0）。

圖6

誤區提示：線面角與直線的方向向量和平面法向量的夾角（銳角）是互余的關系，部分同學在求解此類問題時，因忽略這種關系會將線面角的求解公式記為cosθ=正確的線面角求解公式是其中l，n 分別表示直線的方向向量和平面的法向量。

解決關于向量問題時，一要善于運用向量的平移、伸縮、合成、分解等變換，正確地進行向量的各種運算，加深對向量的本質的認識。二是向量的坐標運算體現了數形結合的思想。用空間向量解決立體幾何問題一般可按以下過程進行思考：①要解決的問題可用什么向量知識來解決? 需要用到哪些向量?②所需要的向量是否已知? 若未知，是否可用已知條件轉化成的向量直接表示? ③所需要的向量若不能直接用已知條件轉化成的向量表示，則它們分別最易用哪個未知向量表示? 這些未知向量與由已知條件轉化的向量有何關系? ④怎樣對已經表示出來的所需向量進行運算，才能得到需要的結論? 從立體幾何解答題的答題情況看，同學們出現“會而不對，對而不全”的現象嚴重（解題中論述不嚴格，條理不清，缺條件，因果關系不成立等）。在平時的訓練中，要注重思維的條理性和表達的規范性，做到分析問題有理有據，表達論證合規合矩。在立體幾何解答題的作答中，防止出現“跳”（步），“離”（圖形與書寫相脫離），“省”（省略關鍵步驟）等現象。乍一看，結果（論）正確，似乎沒有問題，但經不起仔細推敲。在平時訓練中，要做到：符號語言要規范，表達要嚴謹（建系的說明）。分分必爭！ 對照歷年高考閱卷的評分細則和評分標準嚴格做到解題步驟書寫規范，踩點得分，分步得分。要實現：想得清楚，說得明白，寫得干凈。