用空間向量解決立體幾何問題的建系策略

■四川省綿陽實驗高級中學 黃 芹

立體幾何是高中數學知識體系中的重要知識模塊，也是高考重點考查的核心內容之一。空間向量是求解立體幾何問題的一個重要工具，利用空間向量解答立體幾何問題，主要突破“四關”：第一關，建系；第二關，求點的坐標；第三關，求法向量；第四關，應用公式。然而如何建立恰當的空間直角坐標系并求出點的坐標是用空間向量解決立體幾何問題的關鍵所在。下面以典型的幾何體：棱柱、棱錐、多面體為載體，以典型的問題情境設計：求線面角、求二面角、探索性問題、翻折問題為背景，剖析建立空間直角坐標系的常用途徑。

途徑一、利用共頂點的互相垂直的三條棱構建空間直角坐標系

例1如圖1，在直三棱柱ABC-A1B1C1中，△ABC是等腰直角三角形，AC=BC=1，AA1=2，D 是側棱AA1上的一點。

（1）證明：當D 是側棱AA1的中點時，DC1⊥平面BCD。

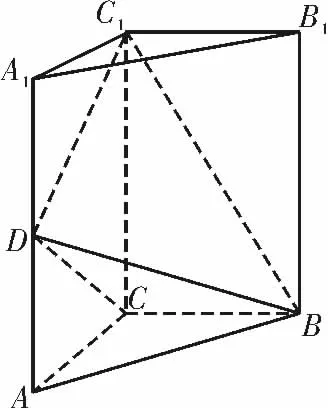
圖1

（2）側棱AA1上是否存在一點D，使二面角D-BC1-C 的余弦值為若存在，請求出AD 的長度；若不存在，請說明理由。

分析：（1）幾何體中有三條直線兩兩垂直，直接建系。（2）空間向量非常適合于解決立體幾何中的探索性問題，只需要建立恰當的空間直角坐標系，通過坐標運算把“是否存在”的問題轉化為“點的坐標是否有解”的問題。

解：（1）證法一：由題意BC⊥AC 且BC⊥CC1，AC ∩CC1=C，所以BC ⊥平面ACC1A1。

又因為DC1?平面ACC1A，所以BC⊥DC1。

又因為D 是AA1的中點，AC=AD，且∠CAD=90°，所以∠ADC=45°。

同理，∠A1DC1=45°。

所以∠C1DC=90°，則DC1⊥DC。

又因為DC∩BC=C，所以DC1⊥平面BCD。

證法二：如圖2，以C為坐 標 原 點，CA，CB，CC1所在直線分別為x軸，y 軸，z 軸，建立空間直角坐標系C-xyz。

由題意知C（0，0，0），D（1，0，1），B（0，1，0），C1（0，0，2），所以

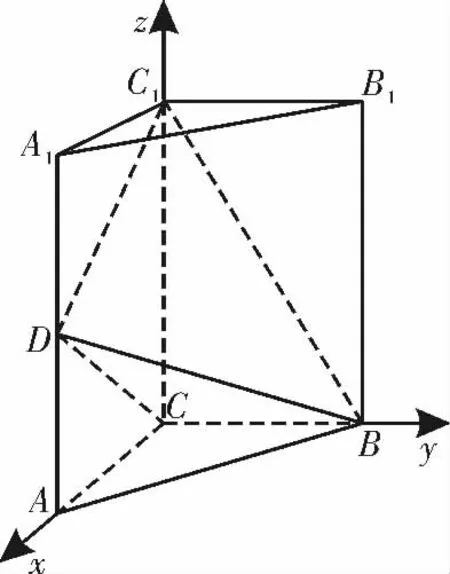
圖2

所以DC1⊥CD，DC1⊥CB。

又CD∩CB=C，所以DC1⊥平面BCD。

（2）假設側棱AA1上存在一點D 滿足題意。

設AD=h（0＜h＜2），則D（1，0，h），B（0，1，0），C1（0，0，2）。

由條件易知CA⊥平面BC1C，故取m==（1，0，0）為平面BC1C 的法向量。

設平面DBC1的法向量為n=（x，y，z），所以

途徑二、利用線面垂直關系，構建空間直角坐標系

例2如圖3 所示，在三棱柱ABCA1B1C1中，△ABC為 等邊三角形，∠BAB1=∠BB1A，AB1∩A1B=O，CO⊥平 面ABB1A1，D是線段A1C1上靠近A1的三等分點。

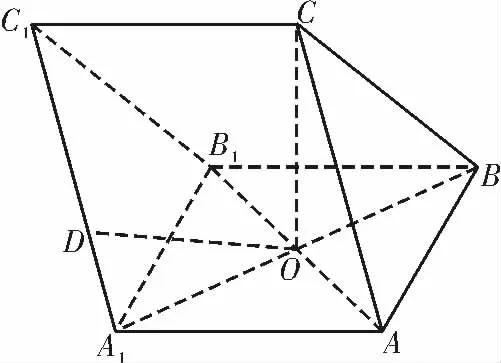
圖3

（1）求證：AB⊥AA1；

（2）求直線OD 與平面A1ACC1所成角的正弦值。

分析：三棱柱放倒，但仍有使用向量法的明顯特征，由條件可得四邊形A1ABB1為菱形，菱形的對角線互相垂直，結合已知條件中的線面垂直關系：CO⊥平面ABB1A1，所以可以以O 為坐標原點建系。由第（1）問的結論也可以B 為坐標原點，z 軸與OC 平行（z 軸懸空）建系，如圖4所示。求點C的坐標可以利用求 點D的坐標可以利用本題第（2）問的解答以O 為坐標原點建系為例。

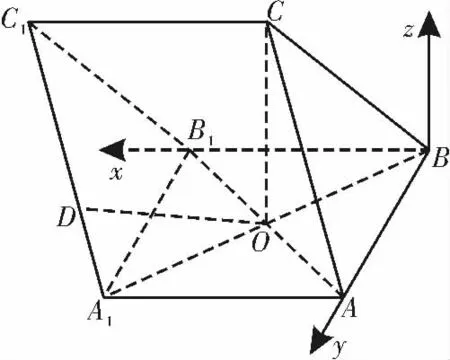
圖4

解：（1）因為∠BAB1= ∠BB1A，所以AB=BB1，所以四邊形A1ABB1為菱形。

因為CO⊥平面ABB1A1，故∠COA=∠COB=90°。

因為CO=CO，CA=CB，所以△COA≌△COB，所以AO=BO，即四邊形ABB1A1為正方形。

所以AB⊥AA1。

（2）依題意，CO⊥OA，CO⊥OA1。

在正方形A1ABB1中，OA1⊥OA。

所以以O 為坐標原 點，OA1，OA，OC 所在直線分別為x 軸，y 軸，z 軸，建立如圖5 所示的空間直角坐標系O-xyz。

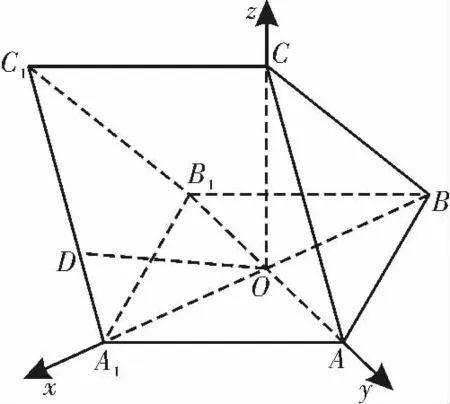
圖5

不妨設AB=2，則O（0，0，0），A1（，0，0），A（0，，0），

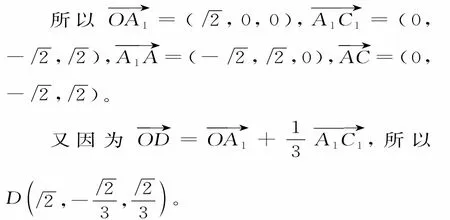
設平面A1ACC1的法向量為m=（x，y，z），所 以令x=1，得y=1，z=1，所以m=（1，1，1）。

所以直線OD 與平面A1ACC1所成角的正弦值為

總結：建系的關鍵是找到垂直關系。判斷線線垂直的常用結論：正方形、矩形、直角梯形；等腰三角形底邊上的中線與底邊垂直；菱形的對角線相互垂直；勾股定理逆定理；線面垂直性質定理等。

途徑三、利用面面垂直關系，構建空間直角坐標系

例3如圖6，在四棱錐P-ABCD 中，底面ABCD 為直角梯形，BC∥AD，AD ⊥DC，BC=CD=1，AD=2，PA=PD，E 為PC 的中點，平面PAD ⊥平面ABCD，F 為AD 上一點，PA∥平面BEF。

（1）求證：平面BEF⊥平面PAD；

（2）若PC 與底面ABCD 所成的角為60°，求二面角E-BF-A 的余弦值。

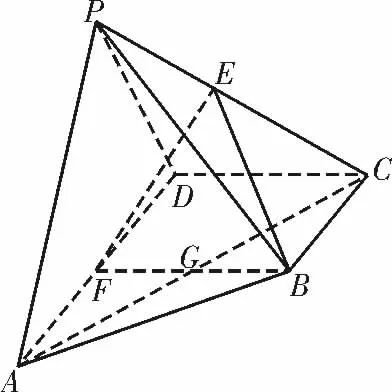
圖6

分析：（1）連接AC 交BF 于點G，連接EG，結合線面平行的性質可得PA∥EG，再由E 為PC 的中點，得G 為AC 的 中點，則△AFG≌△CBG，得到AF=BC=AD=1，即F 為AD 的中點，可得四邊形DCBF 為平行四邊形，再由AD⊥DC，得BF⊥AD，可得BF⊥平面PAD，進一步得到平面BEF⊥平面PAD。（2）由面面垂直轉化為線面垂直，結合底面是直角梯形，可以以D 為坐標原點建系。分析得到F 為AD 的中點，也可以以F 為坐標原點建系。P 點坐標未知，需要先設坐標，比如設P（0，0，t），由PC 與底面ABCD 所成的角為60°可求解t。

解：（1）連接AC 交BF 于點G，連接EG。

因為PA∥平面BEF，PA?平面PAC，平面PAC∩平面BEF=EG，所以PA∥EG。

又E 為PC 的中點，所以G 為AC 的中點，則△AFG≌△CBG，得AF=BC=AD=1，所以F 為AD 的中點。

因為BC∥FD，且BC=FD，所以四邊形DCBF 為平行四邊形。

因為DC⊥AD，所以BF⊥AD。

又BF?平面ABCD，平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，所以BF⊥平面PAD。

又因為BF?平面BEF，所以平面BEF⊥平面PAD。

（2）連接PF，因為PA=PD，F 為AD的中點，所以PF⊥AD。

又PF?平面PAD，平面PAD ⊥平面ABCD，平面PAD∩平面ABCD=AD，所以PF⊥底面ABCD。

又BF ⊥AD，所以以F 為坐標原點，FA，FB，FP 所在直線分別 為x 軸，y 軸，z 軸，建立空間直角坐標系F-xyz，如圖7所示。

設P （0，0，t），則F（0，0，0），C（-1，1，0），

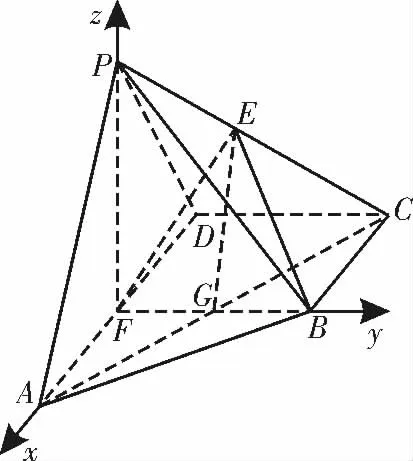
圖7

取平面ABCD 的法向量為n1=（0，0，1），所以

設平面EBF 的法向量為n2=（x，y，z），所 以令z=1，得x=，所以n2=（，0，1）。

總結：先由面面垂直性質定理得到線面垂直，再建立空間直角坐標系。建系時讓一些點、線段盡量與坐標軸重合。在利用法向量解決線面角及二面角大小時，一定要注意正確運用公式，并判斷所求二面角是鈍角還是銳角。

立體幾何解答題通常分步設問，既考查同學們的空間想象能力與邏輯推理能力，也考查運算求解能力。問題情境千變萬化，但萬變不離其宗的是：立體幾何解答題的考查歸結為點、線、面的位置關系，以及角度、距離的求解。空間向量工具是解決立體幾何問題的“尚方寶劍”，空間直角坐標系是“定海神針”，三種建系途徑若能熟練掌握，定能提高分析問題的能力和解題速度。