基于等效模型的鉸制孔螺栓力學設計與優化*

周夕維，陳騰飛，向華平

（南京電子技術研究所，江蘇南京210039）

引 言

螺栓連接形式廣泛應用于工程結構中，特別是那些需要經常裝拆的部件和部位，必須使用螺栓連接。在航空電子產品結構件中，螺栓類連接件的應用則更為普遍[1]。

螺栓連接結構存在的接觸和預緊力等非線性因素對有限元計算結果影響較大。國內外專家學者對螺栓連接結構進行了大量的數值模擬計算和實驗研究。對螺栓連接結構進行模擬計算時，普遍采用三維實體建模法，并對螺栓模型進行細致的網格劃分，以確保數值計算的準確性[2-4]。但是，對于復雜機械結構如多軸伺服轉臺，裝配時會使用大量螺栓進行連接。螺栓數量的增加導致數值模擬計算量顯著增大，計算速度明顯降低。因此，有必要對螺栓模型進行合理簡化，從而提高多螺栓連接模型的計算效率。

本文以某兩軸伺服轉臺為例，通過等效剛度模型對鉸制孔螺栓進行簡化處理，建立系統級有限元模型，仿真得到各處螺栓的三向載荷。根據載荷大小對螺栓布局進行優化，得到布局最優解。在此工況下，按照第四強度理論，對螺栓進行強度和壽命校核，驗證其工程合理性。

1 工程背景介紹

伺服轉臺通過基座與載機平臺連接，驅動負載在規定時間周期內到達指定位置，并保證相應的指向精度。伺服轉臺包括基座、下殼體、電機組件、萬向支架和驅動支臂，其外形見圖1。

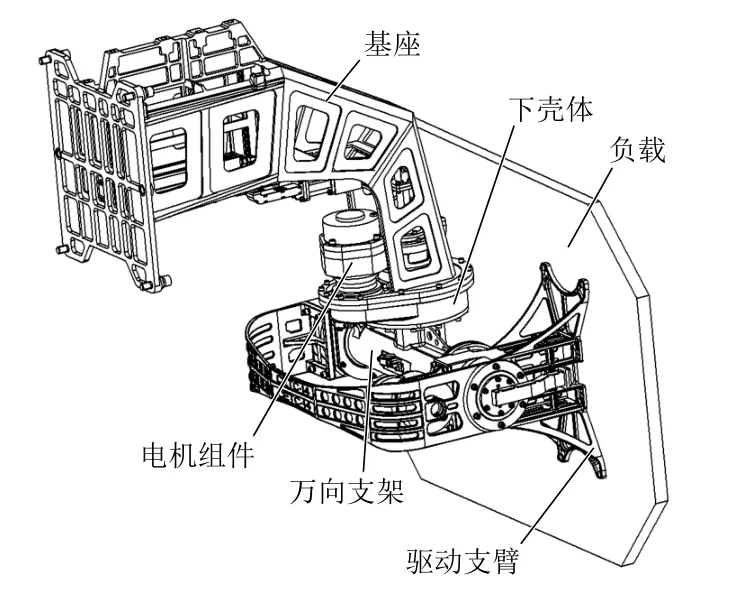
圖1 伺服轉臺外形圖

伺服轉臺與驅動的負載是一個串聯結構，二者形成的組合載荷經由基座傳遞給載機平臺，載機平臺的振動與沖擊載荷也反向通過基座傳遞給整個伺服轉臺。這樣一來，基座和下殼體之間的連接就承擔了系統近95%的載荷，因此其力學設計就顯得尤為重要。同時為了保證良好的裝配精度，基座與下殼體之間通過M6H5 的鉸制孔螺栓進行連接。

基座與下殼體之間的螺栓布局按照連接件剛度匹配原則進行設計，如圖2 所示。對于剛度連續的區域，螺栓對稱密排布；對于剛度不連續的區域，螺栓僅僅起到輔助安裝功能，采用稀疏排列策略[5]。

圖2 基座與下殼體連接螺栓布局

2 有限元力學仿真

2.1 螺栓等效剛度計算

螺栓選擇HB 1-103 型，材料為30CrMnSiA。螺栓連接的基座與下殼體的材料均為2A12（H112）鋁合金，彈性模量E1[6]相同。

對于螺栓的軸向剛度，可以認為在任意垂直于螺栓軸線的截面上的壓應力為均勻分布，將螺栓簡化為空心圓柱體，螺栓的軸向剛度可以表示為：

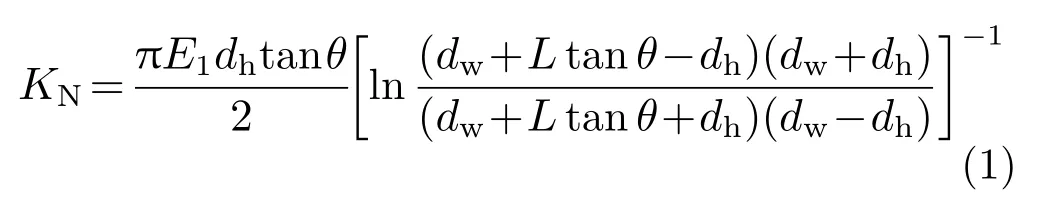
式中：dh為螺栓孔直徑；dw為墊片直徑；L 為連接處基座厚度ts加連接處下殼體厚度tx，即L=ts+tx；θ 為基座和下殼體連接部位壓應力分布的半頂角。

對于螺栓的剪切剛度，基座和殼體之間的連接形式可以認定為搭接形式。螺栓的強度設計將螺栓的承載限定在彈性段內，基于此，螺栓的剪切柔度C 可以表示為：

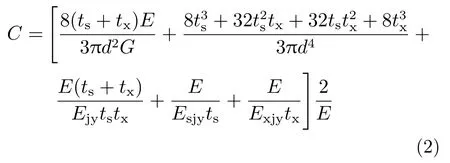
式中：d 為螺栓直徑，由于是鉸制孔，d = dh；E 為螺栓的彈性模量；G 為螺栓的剪切模量；Ejy為螺栓的擠壓模量；Esjy為基座的擠壓模量；Exjy為下殼體的擠壓模量[7]。

螺栓的剪切剛度Kτ為柔度C 的倒數，表示為：

提取模型中基座的厚度ts= 8，下殼體的厚度tx= 10，帶入基座、下殼體及螺栓的材料參數，得到螺栓簡化模型的等效剛度為：

KN=140 000 N·m, Kτ=4 800 N·m

2.2 有限元模型建立

基座與下殼體之間的連接螺栓采用釘元進行模擬，每個釘元使用3 個一維彈簧元進行建模，彈簧的剛度來自螺栓簡化模型的等效剛度。在基座與下殼體配合面的螺栓鉸制孔中心各建立1 個獨立節點，以獨立節點為主節點分別與對應孔壁上所有的節點創建多點約束，約束3 個方向的平動自由度。然后在這兩個獨立節點之間建立彈簧單元，模擬螺栓的軸向拉壓剛度和面內剪切剛度[8]。基座與下殼體連接螺栓簡化情況如圖3 所示，圖中數字為螺栓編號。

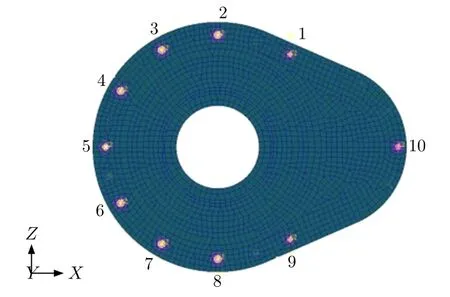
圖3 基座與下殼體連接螺栓簡化模型

按照上述原理及流程對伺服轉臺的其他連接進行同樣處理，最終得到系統的仿真模型，如圖4 所示。

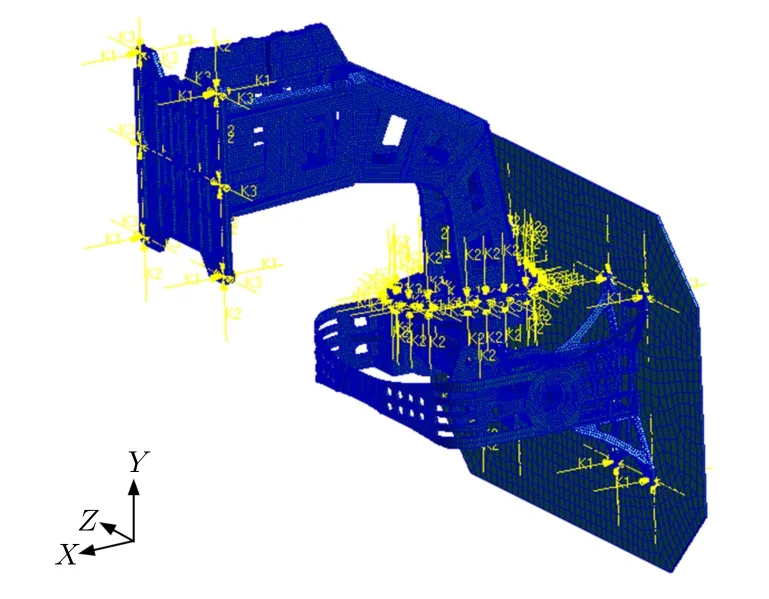
圖4 伺服整體有限元仿真模型

2.3 螺栓應力提取

伺服轉臺工作時需要承受3 軸向后峰鋸齒波沖擊載荷，峰值加速度為20g，脈沖寬度為11 ms。

按照圖4 坐標系定義，選取最為惡劣的Y 向沖擊對伺服轉臺進行系統仿真，提取該方向下各編號螺栓的軸向拉應力與剪切應力，如圖5 所示。

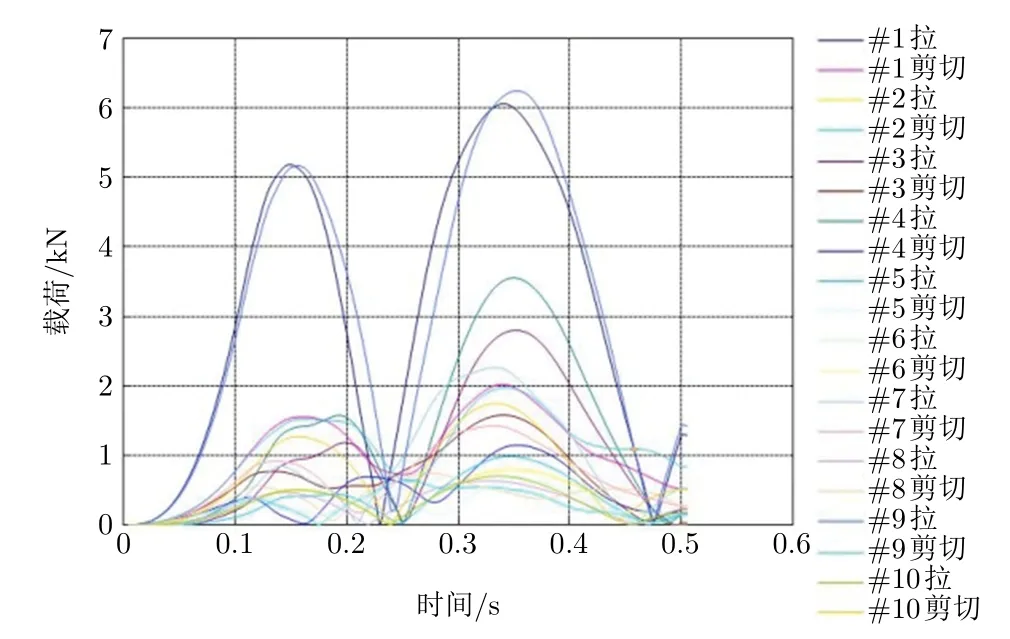
圖5 各螺栓載荷曲線

由圖5 可知，#1 和#9 螺栓相對于其他螺栓，應力水平偏高，這與#1 和#9 螺栓位于傳力主通道邊沿，存在較大的應力集中有關，因此有必要對螺栓分布進行優化。選擇0.35 s 處的應力幅值開展均衡性優化。

3 螺栓布局優化

伺服轉臺的基座與下殼體的連接螺栓位于圖6 所示的黑色中心線上。各螺栓之間的間距和為定值C，C 為本次優化的邊界約束條件。另外，螺栓的間距還需滿足最小扳手空間要求C1。

圖6 螺栓布局邊界曲線

以各螺栓的拉應力均衡性作為優化目標，通過方差函數進行數學表達。以各螺栓之間的間距作為設計變量，同時帶入上述邊界約束，得到本次優化的數學模型，其表達式為：

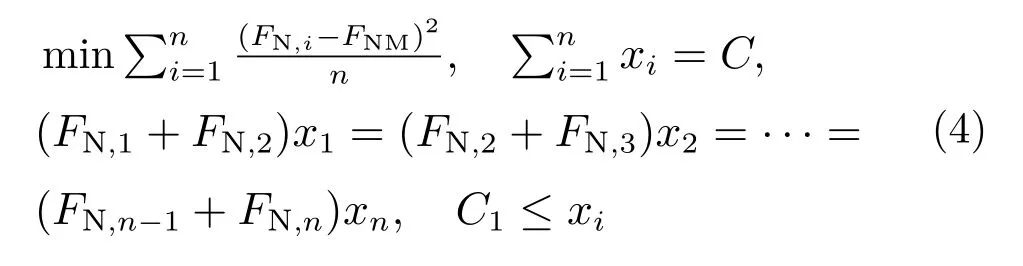
式中：n 為螺栓編號，n = 10；FN,i為編號為i 的螺栓的軸向拉應力；FNM為各螺栓軸向拉應力平均值；xi為i 號螺栓與i+1 號螺栓之間的距離[9]。

固定#10 螺栓位置，帶入已知條件，獲得各螺栓優化后的間距。修訂螺栓孔間距參數，得到圖7 所示的優化后螺栓布局。

圖7 優化后螺栓布局

更新有限元模型后重新計算，得到優化后的螺栓軸向拉應力和剪切應力，如圖8 所示。螺栓最大軸向載荷降低了29.5%，各螺栓的軸向拉應力幅值均衡性已經大幅提升。

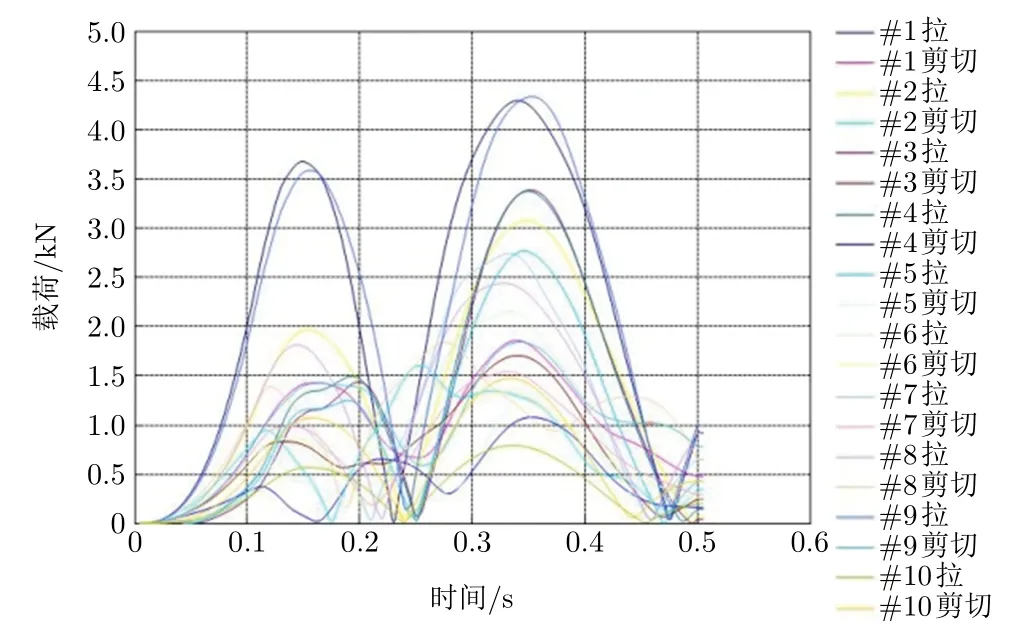
圖8 優化后各螺栓載荷曲線

4 強度與壽命校核

4.1 強度校核

按照軸向拉應力與橫向剪切應力核算螺栓在沖擊載荷下的安全性，螺栓實際的軸向拉應力σ 和橫向剪切應力τ 可以表示為：

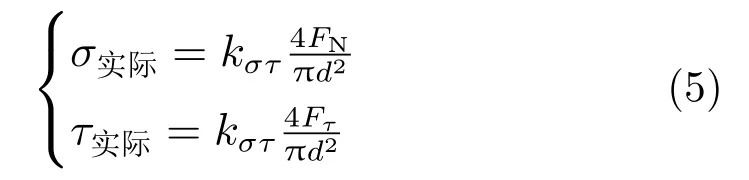
式中：kστ為仿真修正系數；FN為軸向載荷，本次核算取時間周期內的最大值；Fτ為剪切載荷，本次核算取時間周期內的最大值。

根據各螺栓載荷曲線，FN= 4 338 N，Fτ=1 862 N。取kστ=1.3，d=6 mm。帶入式(5)得到：

σ實際=199.4 MPa, τ實際=85.6 MPa

螺釘材料為30CrMnSiA，材料的許用軸向拉應力[σ] = 0.7σs= 716 MPa，材料的許用剪切應力[τ] = 0.25σs= 256 MPa，σs為材料屈服強度。由于螺釘承受交變載荷，因而取許用安全系數[S] = 2.5對螺栓強度進行校核：

σ名義=[S]×σ實際=498.5 MPa ＜[σ]

τ名義=[S]×τ實際=214.0 MPa ＜[τ]

因此，優化后螺栓滿足強度設計要求。

4.2 壽命校核

根據第四強度理論，螺栓組合應力可以表示為：

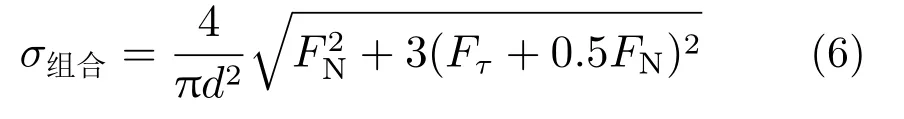
按照保守原則，FN和Fτ取4.1 節中的最大值。帶入這些已知條件得到：

σ組合=290.6 MPa

根據螺栓的材料，螺栓的疲勞強度可以定義為：

式中，σb為材料抗拉強度。帶入材料數據，得到：

σ?1=529 MPa

考慮螺栓的加工因素及應力集中情況，螺栓可以承受的疲勞極限應力幅值為[10]：

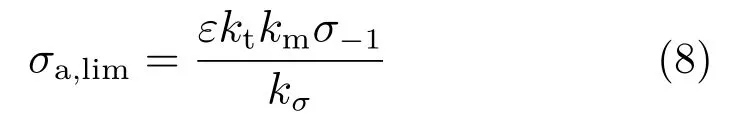
式中：ε 為尺寸系數，取1.1；kt為螺紋制造工藝系數，取1.4；km為螺紋材料系數，取1.4；kσ為螺紋應力集中系數，取1.3；取安全系數[S] = 2.5，得到螺栓的疲勞許用應力幅值為：

因此，優化后螺栓的疲勞壽命滿足設計要求。

5 結束語

本文以某伺服轉臺為例，詳細介紹了系統級產品內部螺栓的載荷獲得、應力提取、布局優化、強度校核及壽命預測的設計全流程。相比傳統有限元仿真，該方法具有以下突出優勢：

1）相較于純理論核算，可以有效體現螺栓的承載不均衡性，降低預測誤差；

2）相較于詳細模型核算，大大減少了有限元建模工作量，減少了計算資源消耗，從而大大提升了有限元仿真校核工作效率；

3）可以快速獲得螺栓的優化布局，降低螺栓間承載的不均衡性，從而大大提升連接可靠性。

該方法對同類工程問題具有一定的應用價值。