展示性學習視角下數學圖形特征的探索

仇小婉 段志貴

【摘 ? 要】展示性學習有助于學生實現自我，與其他學習者共同成長。把展示性學習應用于“三角形三邊關系”教學之中，靈活運用“做”“展”“啟”“練”“評”等方式方法，引導學生發現圖形特征，體會三邊關系，能夠充分調動學生的學習積極性、主動性和創造性，有效構建師生、生生自由平等交往的生態化課堂環境，培養學生的數學思維，提高學生的數學素養。

【關鍵詞】展示性學習;數學圖形特征;三角形三邊關系

展示性學習是一種凸顯兒童自主學習與合作交流的學習方式，具體地說，它是個人或學習共同體通過向他人展示知識、方法、疑難、困惑等，以實現自我，和其他學習者共同成長的學習方式[1]。下面以蘇教版四年級下冊《三角形三邊關系》一課為例，分析展示性學習方式在數學圖形特征探索活動中的具體應用。

一、展示性學習的教學構思

雖然每名學生的成長環境不同、個性不同，表現出的基礎特質也不相同，但他們各有各的優勢，各有各的不足。誠如美國著名學者、心理學大師唐納德·克利夫頓所說，“教育的目的就是發現優勢并發揮優勢”，學校教育就是要喚醒他們，激勵他們，讓他們保持和發揚優勢，修正或彌補不足。本質上，展示性學習就是要讓每名學生都有展示的機會，使他們能夠充分發揮自己優勢并在學習的過程中逐步建立起成長的自信。相比傳統的小組合作學習，展示性學習不僅關注小組內知識和方法的交流，還注重小組代表和全班同學的交流學習，學生可以在辨析與交流中豐富學習內容，進行更深度的學習思考。因此，扎根于“喚醒—展示—成長”理念的展示性學習策略在小學數學教學中的運用，具有十分重要的現實意義和實踐價值。

三角形的三邊關系特征，即任意兩邊之和大于第三邊，是學生在學習三角形定義之后對三角形“邊”基本特征的初次研究。教學上采用展示性學習的方式，組織學生開展動手操作——圍三角形的探索活動，并讓學生先后在小組和全班進行展示交流，再通過教師的有效點撥及有針對性的鞏固訓練，促進學生更深入地理解三邊關系的數學本質。

二、展示性學習的推進過程

展示性學習的實施主要包括合作探究、 展示交流、精講點撥、有效練習和創新評價等具體策略，常常簡稱為“做”“展”“啟”“練”“評”。這五項策略并非完全割裂，也不固化為固定的時間、統一的模式，而是可以根據實際需要靈活推進，優化組織。一般情況下，“做”在展示之前完成，“展”“啟”“練”“評”交互進行。在小學數學圖形特征的展示性教學中，教師著重組織以下三個環節的教學。

（一）小組合作，展示前“做”中學習

上課初始，教師首先讓學生任意選取小棒圍三角形，發現有能圍成三角形和不能圍成三角形兩種情況，在此基礎上順勢而教，引導學生研究三角形三邊長度關系。

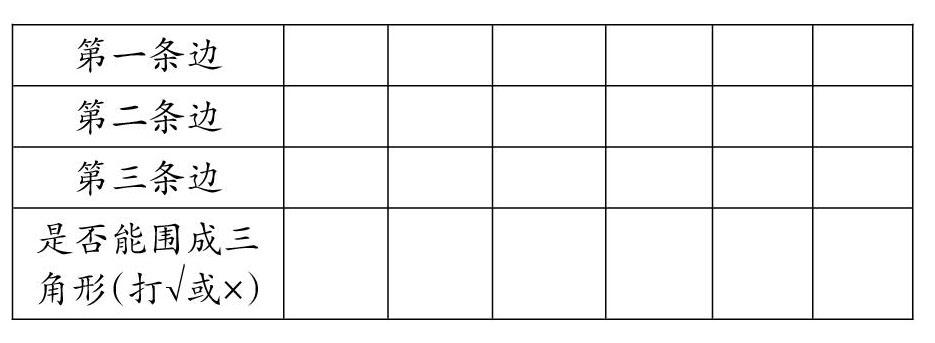
小組合作1：從學具內任意選擇3根顏色不同的小棒，圍一圍，并記錄在學習單上。

[第一條邊 第二條邊 第三條邊 是否能圍成三角形（打√或×） ]

學生選擇顏色不同的3根小棒獨立圍三角形，小棒顏色不同即長度不同，同時請小組記錄員將每人圍的情況一一記錄下來，教師在組內巡視指導。

小組合作2：從圍成三角形的小棒中任選2根，和第3根比一比，你發現了什么？

學生觀察比較圍好的三角形，思考三角形中任意2根小棒與第3根的關系。

小組合作3：剛剛我們只是從3個三角形中發現任意兩邊之和大于第三邊，能說明所有三角形都這樣嗎？（不能）這只是我們的猜想，還需要通過更多的例子來加以驗證。怎么驗證呢？小組討論交流。

小組的有效交流應基于對所有學生動手操作結果的展示與思考。只有每名學生都有機會動手操作，課堂展示才會呈現出真實性和多樣性。如果僅靠一兩個小組與教師的互動交流完成學習，那么課堂呈現出的是虛假的熱鬧，不利于全體學生發展。因此，在展示前小組內應先進行分工，組內成員一起動手操作圍三角形，獲得體驗，并初步形成猜想，為真實有效的課堂展示打下基礎。

（二）激發思考，在“展”“啟”中提升思維

匯報展示1：小組合作完成第一個任務后，請各小組匯報展示圍三角形的情況。

第一小組：我們小組用10厘米、6厘米和8厘米這三根小棒圍成了1個三角形，用4厘米、5厘米和6厘米這三根小棒圍成了1個三角形，還用5厘米、6厘米和8厘米小棒圍成了三角形。

師：那有沒有小組沒能圍成三角形的？

第四小組：我們小組用4厘米、6厘米和10厘米這三根小棒沒圍成三角形。

師（點頭）：嗯，怎么會出現這種情況呢？其他小組呢？

第五小組：我們小組用10厘米、4厘米和5厘米也沒能圍成三角形。

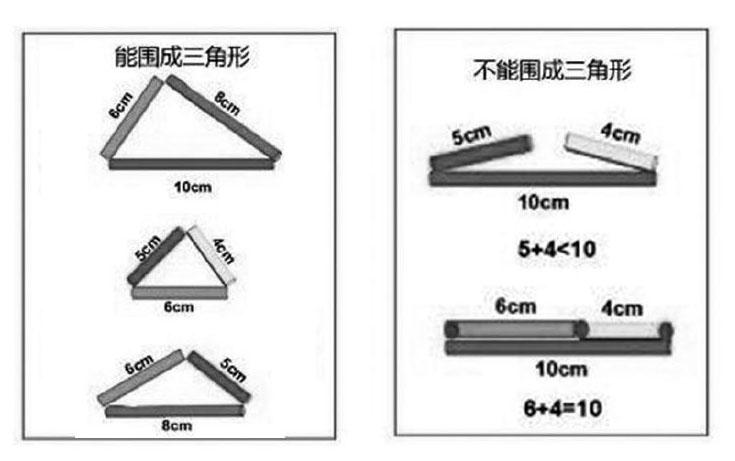
師：我們來看一下，為什么這兩種情況不能圍成三角形？

學生展示圍三角形的各種情況后，教師引導學生先研究三根小棒不能圍成三角形的情況，發現用數學算式表示這兩種情況中三根小棒長度關系，分別是4+5<10和6+4=10，進而猜想能圍成三角形的三根小棒的關系：兩根小棒的長度加起來大于第三根小棒的長度。

匯報展示2：比較三角形中任意兩根小棒與第三根的關系。

小組匯報：我們小組先研究第1個三角形，6+8>10，6+10>8，8+10>6。然后研究第2個三角形，4+5>6，6+4>5，6+5>4。最后研究第3個三角形，5+6>8，5+8>6，8+6>5。我們小組發現：三角形中任意兩根小棒長度之和大于第三根小棒的長度。

師：在三角形中，小棒其實相當于三角形的邊，我們還可以換一種說法：三角形中任意兩邊之和大于第三邊。這句話中“任意”是什么意思？

這里教師的追問即為“啟”。“啟”很重要，是提升學生思維層次的關鍵環節，不能錯過。

師：剛剛在比較時我們有沒有體現出“任意”？

學生思考片刻，逐漸理解：在比較三角形兩邊之和與第三邊關系時，對應寫出三道算式，將三種情況都進行比較，這就是“任意”的體現。

師：可是每次比較時都寫這么多算式很麻煩，有沒有簡單點的方法？

生：其實只要寫出一道就可以了，第1個三角形中只要寫出6+8>10，第2個三角形只要寫4+5>6。

師：為什么？

生：這是比較了較短的兩邊之和與第三邊的長度。較短兩邊之和都大于第三邊了，三角形中其他任意兩邊之和肯定大于第三邊。

教師隨即點撥：既然有較短邊，相應的就有最長邊。我們在比較時不需要把所有情況都寫出來，只要比較短兩邊之和與最長邊之間的關系就可以了。

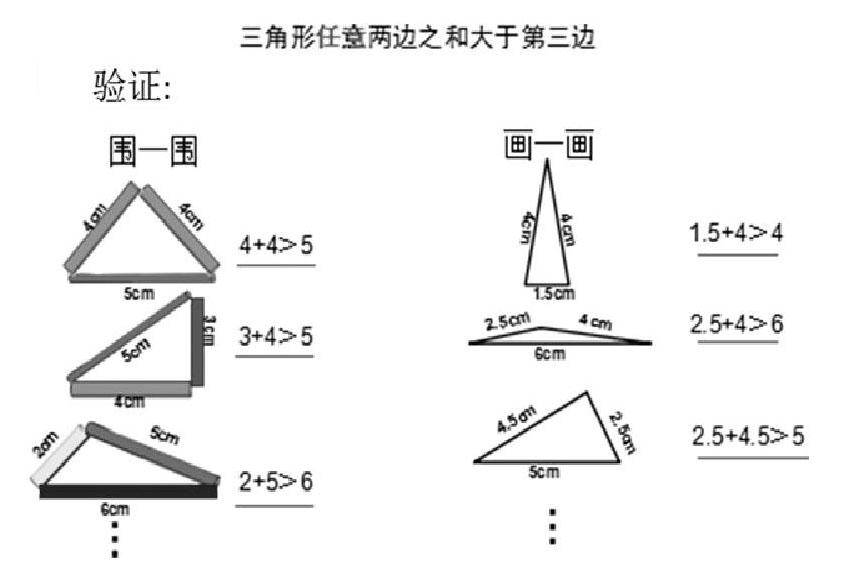
匯報展示3：由3個三角形的三邊關系初步提出猜想后，在組內驗證其他三角形是否也滿足這一猜想，并介紹交流驗證的過程和結果。

以上教學過程，教師引導學生通過動手操作和不完全歸納，在眾多實例中發現其他三角形同樣滿足這一猜想，并且沒有出現反例，大家形成共識：三角形任意兩邊之和大于第三邊。其中，在驗證猜想時，學生通過自己畫三角形發現：三角形三邊的長度不僅可以是整數，小數也同樣適用，擴大了三角形三邊的取值域。

（三）鞏固訓練，在“練”“評”中深化認知

練習1：從學校到少年宮有幾條路線可以走？走哪一條路最近？

練習1的解決并不困難，重在通過問題解決發展學生的推理能力。學生提出猜想，并通過舉例驗證獲得結論的方法是一種合情推理。在小學教學中很多地方會用到合情推理，但合情推理的結果本身不夠嚴謹，所以教師在進一步的討論中隱去“學校—郵局—少年宮”的路線，引導學生觀察上面的三角形，感受從“兩點之間線段最短”得出“三角形任意兩邊之和大于第三邊”的演繹推理思想。這樣合情推理與演繹推理相輔相成，凸顯思維的創新與躍進，符合學生的思維特點，幫助學生從另一個角度再次探索知識，感受數學的趣味性，增強思維的靈活性。

練習2：（1）李叔叔打算從8厘米、5厘米、4厘米和3厘米長的小棒中，選擇3根小棒釘成1個三角架，可以選擇哪3根？

學生選擇3根小棒，并自覺用算式驗證是否能圍成三角形。

（2）李叔叔最后選擇了8厘米、5厘米和4厘米的小棒，如果把其中的4厘米小棒換掉，可以換多長的？

教師結合視頻，幫助學生理解在比較三角形任意兩邊和與第三邊時，最長邊不一定是固定的，而是可以變換的。將8厘米看作最長邊，第三邊要大于3厘米卻不超過8厘米;也可以將第三邊看作最長邊，這時第三邊大于等于8厘米，卻要小于13厘米。由此得到第三邊的取值范圍：小于已知兩邊之和，大于已知兩邊之差。

以上練習能幫助學生在思考中提升對知識的理解，深入理解三角形三邊關系，自覺檢驗三角形第三邊的范圍，感受解決問題過程中數學思維的層次性和操作方法的靈活多樣性。

三、展示性學習的教學反思

（一）尊重學生主體地位是展示性學習的前提

本節課基于學生是學習的主體，教師是學生學習的組織者、引導者、促進者的基本理念，放手讓學生自主探索、匯報展示和交流。通過獨立圍三角形、小組展示、提出猜想、舉例驗證并獲得結論這一過程，學生得以充分展示自主學習的成果。自由發言、動手操作等活動貫穿始終，激發了學生學習的內驅力。正因為有對學生主體地位的尊重，才有后面課堂中展示匯報的精彩。課堂上每個人都積極參與，認真思考，群策群力，課堂氛圍活潑真實，有效地提高了學習效率，增強了學習效果。

（二）實現全體學生共同發展是展示性學習的目標

本節課學生先獨立圍三角形，然后以小組展示匯報為平臺，通過展示，調整完善自己的認知;通過傾聽同伴的補充發言，形成新的信息。“任意”是數學推理中重要的詞語之一，多數學生頭腦中原本的“任意”指隨意、隨便的意思，他們并沒有深入理解本質。小組討論并闡釋對“任意”的理解，從語言、算式等不同方面相互交流，學生在吸收集體智慧的過程中，又反過來促進集體的發展，進入新一輪的學習，在這種生生對話、師生對話中實現對“任意”的深入理解。這種學習展示體現了生命的兩種本性：作為個體的自我需要成長、發展，作為群體中另一個自我需要交流、欣賞或被欣賞、評價或被評價。如此，每個人在數學上都獲得不同的發展，整個學習共同體在課堂教學中煥發了生命的自然活力。

（三）開展行之有效的探究活動是展示性學習的載體

本節課的教學目標之一是引導學生理解和掌握三角形的三邊關系特征，即任意兩邊之和大于第三邊。教學上采用小組合作的形式，沿著猜想—驗證—結論—應用這一線索組織學生通過組內和組際間的互動與展示，開展動手圍三角形的探索活動，在活動中教師輔以示范與啟發，引導學生發現圖形特征，體驗三角形任意兩邊之和大于第三邊。如果不安排圍三角形的活動，也不匯報展示圍的情況并比較三角形的三邊關系，而是直接告訴學生結論，盡管也能完成教學，但學生的體驗和理解不會如此深刻，綜合能力得不到明顯提高，學習效果也不會像現在這樣顯著。開展行之有效的探究活動，可以促進展示性學習，充分調動學生主動性和創造性，構建師生、生生自由平等交往的生態化課堂環境。

綜上，在展示性學習視角下開展圖形特征的探索，促使學生不僅可以從被動地“聽”轉向主動地“做”，擁有更多自由表達、與他人交流的機會，獲得對數學知識的深度理解，還可以通過小組共同合作和展示，對自己所在小組產生歸屬感，改變全班學習氛圍，讓知識、能力和情感自然發展，互相促進。

參考文獻：

[1]汪小珍.展示性學習：自主學習的一種樣態[J].教育研究與評論，2020（2）：23-24.

[2]韓立福.展示對話學習 ? 煥發生命活力[N].中國教育報，2012-08-09.

（江蘇省南京市將軍山小學 ? 210012

鹽城師范學院數學與統計學院 ? 224002）