關于分數階微積分算子的新進展
王秋爽,徐 潤
(曲阜師范大學 數學科學學院,山東 曲阜 273165)
分數階微積分是關于任意階微分與積分及其應用的理論,是牛頓-萊布尼茲整數階微積分的推廣。1987年,Samko等建立了系統的分數階微積分及其應用理論[1]。1993年,Miller等建立了分數階微分方程理論[2],對幾類經典的分數階微積分算子定義均有介紹,例如Riemann-Liouville(R-L),Caputo,Hadamard 分數階微積分算子定義等。許多學者隨后又給出了關于分數階微積分以及分數階微分方程理論的推廣,如文獻[3-6]。近年來,隨著相關分數階積分和導數新定義的不斷引入和推廣,關于分數階和分和差分以及分數階偏微分、偏差分等幾類新的分數階算子也陸續產生,極大地推動了關于分數階微分方程定性性質的研究,如解的振動性、穩定性、解的存在唯一性等。同時由于具有各種初值或邊界條件的分數階積分和分數階微分方程在實際問題中的廣泛應用,分數階方程理論得到了快速發展,并為解決一些復雜現實問題提供了工具。Oliveria等介紹了自分數階微積分出現以來的一些重要分數階積分和導數定義[7];Teodoro等對一些重要分數階導數定義進行了總結,并且對其之間的一些重要性質做出比較[8]。本文主要介紹了近三年所出現的分數階積分和微分算子新定義,并比較了各不同定義之間的關系。
1 預備知識
本文所用到的符號和定義如下:
R為實數集,C為復數集,Z為整數集,N為自然數集,R(x) = {Rex|x∈C},Z-為負整數集;N-為全體非正整數集,[x]=max{z∈Z:z≤x}。
(1)階乘冪函數
分別為上升階乘 (遞進階乘) 和下降階乘 (遞降階乘)。
(2)廣義Mittag-Leffler(M-L) 函數
(1)
其中,α,β,γ,τ,c∈C;R(c),R(α),R(β),R(τ),R(γ) > 0;k>0,p≥0;0 為Gamma函數; 為推廣的Beta函數[9]。 (3)k-Gamma函數 其中,(x)n,k=x(x+k)(x+2k)…(x+(n-1)k)為k-階乘冪函數[10]。 (4)區間值函數 記K={[a,b]×[c,d]|a,b,c,d∈R,a≤b,c≤d}為R上閉區間集族,設 自R-L分數階微積分算子產生以來,許多學者對分數階微積分算子定義進行了完善和推廣,例如2006年Jumarie給出了修正的R-L分數階導數定義[12],使其滿足常數函數的導數為零等。關于分數階微積分算子定義的推廣,大部分的分數階導數定義是由積分構成的,其中最經典的是R-L和Caputo分數階導數,R-L分數階積分算子是由Cauchy公式在實數域上推廣得到,利用R-L分數階積分算子與整數微分算子不同順序的復合分別得到R-L分數階微分和Caputo分數階微分算子。 對于將整數階微積分概念延拓到實數乃至復數的方法有很多種,而大多數的分數階定義是在R-L分數階算子定義的基礎上進行推廣的,分數階微積分算子定義的產生過程大致可以分為四種形式。第一種是在R-L分數階積分定義中利用不同的核函數得到 (實質上是對Cauchy公式的變形并推廣產生) 積分算子,通過對積分算子與整數階微分算子的復合得到微分算子,例如:Hadamard、Katugampola、Prabhakar分數階微積分算子等。第二種是整合分數階微積分算子的產生,首先出現的是整合分數階微分算子,它是對整數階導數定義的自然推廣,而整合分數階積分算子是反常積分的推廣;隨后Jarad 等和Khan等[13-14]通過迭代不同形式的整合分數階積分算子得到整合算子的進一步推廣。第三種是通過對Γ函數的變形得到新的分數階微積分算子定義,例如k-和q-分數階微積分算子等。第四種是對不同分數階微積分算子進行組合,例如Caputo-Katugampola、Caputo-Erdélyi-Kober、ψ-Caputo、ψ-Hilfer、ψ-Atangana-Baleanu、ψ-Prabhakar、Hadamard-k、ψ-k、(k,s)-整合等分數階微積分算子。 隨著分數階微積分算子定義的不斷推廣,在形式上越來越復雜,但在一些性質和應用上有了進一步的優化,并且一般可以退化回經典的分數階微積分算子定義。 2018年, 文獻[9]提出含有個參數的廣義 M-L函數 (見式(1)),并給出了核內含有該廣義M-L函數的左右定新分數階積分算子,是對核含有 M-L函數的分數階積分的進一步推廣;2020年,Farid[15]給出了這類新的分數階積分算子更一般的形式: 設f,k分別為[a,b]→R(0 (2) (3) 注1 若γ(x)=xτ,分數階積分算子(2)(3)是以下算子的推廣:當k(x)=x,ω=p=0時為R-L分數階積分算子;當k(x)=x時為文獻[9]中定義的分數階積分算子;當k(x)=x,p=0時為核包含六參數M-L函數的分數階積分[16];當k(x)=x,l=r=1時為核包含五參數M-L函數的分數階積分[17];當k(x)=x,p=0,l=r=1時為核包含四參數M-L函數的分數階積分[18];當k(x)=x,p=0,l=r=q=1時為核包含三參數M-L函數的分數階積分[19]。 文獻[20]給出左定、右定等Hadamard區間值分數階二重積分: 設F∈IR([a,b]×[c,d]);a,c≤0;α,β>0,定義Hadamard區間值函數分數階積分 (4) (5) (6) (7) 并給出左定、右定等廣義區間值分數階二重積分: 設F∈IR([a,b]×[c,d]);α,β>0;g:[a,b]→R為(a,b]上的單增正函數,且在(a,b)上有連續導函數g′(x);ω:[c,d]→R為(c,d]上的單增正函數,且在(c,d)上有連續導函數ω′(y),廣義區間值函數分數階二重積分定義為 (8) (9) (10) (11) 2014 年,Khalil等第一次給出整合分數階微積分算子定義[21],其中整合分數階積分算子為Riemann反常積分的推廣: 2019年Khan等通過迭代該形式的整合分數階積分算子,得到廣義整合分數階積分[13]。 設f(x)為[p,q]?[0,∞)上整合可積函數,f(x)的β階左定、右定廣義整合分數階積分定義為 (12) (13) 其中,參數α∈(0,1],τ∈R,α+τ≠ 0。 由整合分數階微分算子和廣義分數階積分算子的復合得到左、右定廣義整合分數階微分算子 (14) (15) 其中,Tα為文獻[21]中定義的α階整合微分算子,參數α∈(0,1],p≥0,0<β<1。 注3 定義(12)(13)可退化為以下分數階積分算子:當τ=0時,退化為文獻[14]中定義的R-L型整合分數階積分算子;當α→0時,將得到Hadamard分數階積分算子[2];當α=1時為R-L分數階積分算子[2];當β=1時為整合分數階積分算子[21]。 2017 年,Jarad等提出一種R-L型整合分數階算子[14];在此基礎上,2019年,Mubeen等定義了一類廣義k-分數階積分算子(稱為(k,s)-分數階整合積分算子)[22]。 設f(x)為[0,∞)上的連續函數,α∈C且R(α)>0,參數k>0,s∈R{0},則f(x)的α階(k,s)-分數階整合積分定義為 (16) (17) 注4 對于α>0,p≥1,且f滿足對于任意的x>a成立 則定義的(16)(17)可退化為已有的分數階積分算子。當k=1 時,(16)退化為文獻[14] 中定義的左定整合分數階積分;當a=0,k=1,s=1 時,(17)為左定R-L分數階積分[2];當a=0,α→0 時,退化為Hadamard分數階積分[2];當a=0時,退化為廣義的Katugampola分數階積分[5]。 Tun?等對文獻[23]中定義的廣義k-R-L分數階積分 ((k,s)-分數階積分)做了進一步的推廣,提出與另一個函數ψ有關的(k,s)-R-L分數階積分算子定義,記作ψ-(k,s)-R-L分數階積分[24]。 設ψ:[a,b]→R為(a,b]上單增正函數,且ψ′(x)在(a,b)上連續,左定、右定ψ-(k,s)-R-L分數階積分定義如下: (18) (19) 其中,參數λ,ρ>0;ω∈R;k>0。F的定義如下: 系數σ(m)(m∈N0=N∪{0}) 為有界正實數序列。 注5 分數階積分算子(18)(19)可以退化為已有分數階積分算子:當λ=α,σ(0)=1,ω=0,k=1,ψ(x)=x時,為R-L分數階積分算子[2];當ψ(x)=lnx,λ=α,σ(0)=1,ω=0時,為Hadamard分數階積分算子[2];當k=1,g(t)=t時,(18)和(19)分別退化為文獻[29]、文獻[30]中定義的廣義分數階積分算子;當k=1,λ=α,σ(0)=1,ω=0 時,為ψ-R- L分數階積分算子[2];當ψ(x)=x,λ=α,σ(0)=1,ω=0時,為文獻[26]中定義的k-分數階積分算子;當 時,為文獻[23]中定義的(k,s)-分數階積分算子;當 時,為Katugampola分數階積分算子[5]。 2020年,Sarikaya等給出一類更一般的分數階積分算子[25] (20) (21) 其中Φ:(0,+∞)→[0,+∞)。對于A,B,C>0;θ1,θ2>0滿足: (22) 或 時,是Katugampola分數階積分算子[5];當Φ(θ)=θ(x-θ)α-1時,是文獻[21]中定義的整合分數階積分算子;當 或 在文獻[25]定義的廣義分數階積分的基礎上,Kashuri等提出一類新的廣義整合分數階積分算子[27]: (23) (24) 其中Φ滿足式(22)。 注7 當ζ=1 時,(23)(24)退化為上面定義的廣義分數階積分。 Rahman等定義了一類左定、右定廣義比例Hadamard分數階積分[28]: (25) (26) 其中,比例指數μ∈(0,1],β>0。 注8 當μ=1時,式(25)(26)退化為Hadamard分數階積分[2]。 對分數階微積分近三年來新的算子定義進行了總結,并在此基礎上與已有的微積分算子做了比較。新的分數階微積分算子的產生對于分數階變分、最優控制和復雜系統建模等問題的發展起到了一定的推動作用。相應地,分數階不等式的已有結果可以在新的分數階微積分算子中得以繼續研究。例如文獻[9,15,20-23,25,27-29,31]給出Hermite-Hadamard、Gronwall-Bellman等不等式在新分數階積分算子上的推廣;同時對于新的分數階微分定義可以研究相應分數階微分方程的定性性質[14,18,21]。更深一步地,對分數階微積分算子新定義的研究可以推廣到分數階和分與差分,乃至分數階偏微分以及偏差分的相關問題,通過對這些算子的一些性質進行研究,得到相應分數階差分偏差分等方面方程及不等式的結果。
2 分數階微積分算子新進展
2.1 積分核含有廣義M-L函數的左定和右定分數階積分
2.2 區間值函數的分數階積分
2.3 廣義整合分數階積分和導數
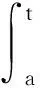
2.4 (k,s)-分數階整合積分
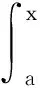
2.5 ψ-(k,s)-Riemann-Liouville分數階積分
2.6 廣義分數階積分
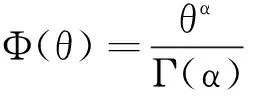
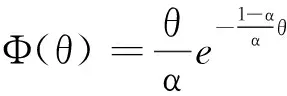
2.7 新的廣義整合分數階積分(廣義FCIO)
2.8 廣義比例Hadamard分數階積分
3 結論

