基于Python語言路徑分析矩陣算法運演

鐘志強 張毅寧

（鞍山師范學院物理科學與技術學院，遼寧 鞍山 114007）

1 引言

多元回歸是一種簡單的因果關系分析，其偏回歸系數（partial regression coefficient）表示在控制其他自變量的條件下，每個自變量單獨對因變量的作用。其中各個自變量處于相同地位，對因變量的作用是并列。如果在兩個變量之間加上中介變量，一個變量既是自變量又是因變量時，存在多個環節，這就構成路徑。多元回歸就不能兼顧這種因果關系。

路（通）徑分析(Path Analysis,Sewall Wright,1921)是相關系數分解的一種統計方法，不僅揭示自變量xi(i=1,2,…m)與因變量y的直接影響力和間接影響力，而且可以在xi,y間的復雜關系中，從某個自變量與其他自變量的“協調”關系中得到對y的最佳影響的路徑信息。目標是探索是事物內在因果關系規律，將因變量與自變量的相互影響的相關系數分解為直接效果的路徑系數和間接效果的路徑系數。這使對模型中的變量的因果關系分析研究更為具體和深入。

路徑分析早期在經濟學領域，被稱為聯立方程模型(simultaneous equation modeling)[1]，多用來分析價格等經濟相關統計數據之間的關系[2,3]。國內相關文獻中，路徑分析研究主要體現在農林科學研究中[4,5],其實現技術有Excel,SPSS,SAS[6-10]。當下，受結構方程模型影響，學者們開始利用R語言（如利用“lavaan”和“semPlot”包）與Mplus工具通過潛變量和中介關系進行路徑分析研究[11]。但當其研究顯變量和無獨立中介模型時，卻要退回利用Excel計算，或利用引入截距項的回歸算法和檢驗方式進行路徑分析。如此造成了研究上的不方便與不科學。本文利用Python語言，實現借助矩陣算法計算決定系數和完成F檢驗，以期進一步說明路徑系數的意義。

2 路徑回歸系數計算

2.1 路徑回歸是標準化的偏回歸系數的推導

y=b0+b1x1+…+bn xn+e

其中bi是自變量xi對因變量y的偏回歸系數。由于各自變量本身變異程度和量綱的不同，使得偏回歸系數絕對值并不能準確反映相應自變量對依變量相對貢獻的大小。為此需將各偏回歸系數標準化，即用相應自變量的標準差與因變量的標準差之比去乘以各偏回歸系數，因而路徑系數為標準的偏回歸系數pyxi，即為自變量對因變量y的直接通徑系數。其推導如下：

由于

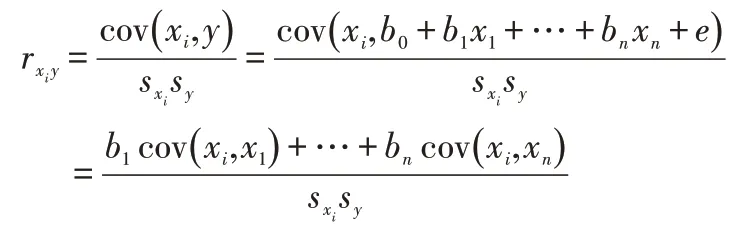
當i=1時，

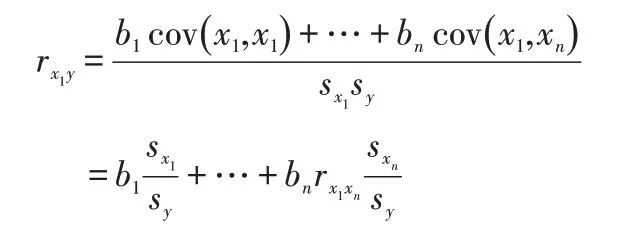
其度量各自變量對因變量的直接效應，其意義上是其它自變量保持不變時，該自變數變動一個單位時，因變量y變動的標準單位數，它不受度量單位和自變量變異程度的影響。

2.2 利用矩陣計算路徑回歸系數

如有三個自變量時：

其中r xiy，rxixj都可以通過已知數據計算得出。令

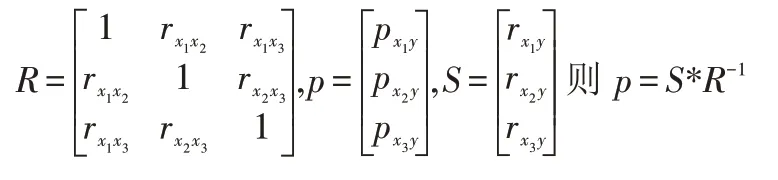
三個自變量的全體路徑系數為P矩陣表示方式為：

這里r x1x2px2y是自變量x1通過自變量x2對y的間接效應。間接通徑系數即自變量xi通過其它相關變量對因變量y的影響，系直接路徑系數乘以二者的相關系數rij pyj。其總間接通徑效果為：

2.3 計算路徑回歸系數Python實現

用于分析的數據“pathdata.csv”為多個參考文獻利用(小麥豐產3號各性狀與單株籽粒產量或腰果種子發芽普遍期天數與氣溫)數據[12-14]，在網絡中亦可得到，見附錄1。其有一個因變量（y）四個自變量（x1-4）,四個自變量間互相關，沒有獨立中介變量。計算路徑回歸Python程序如下（其中變量名與文中公式標識一致，下同）：

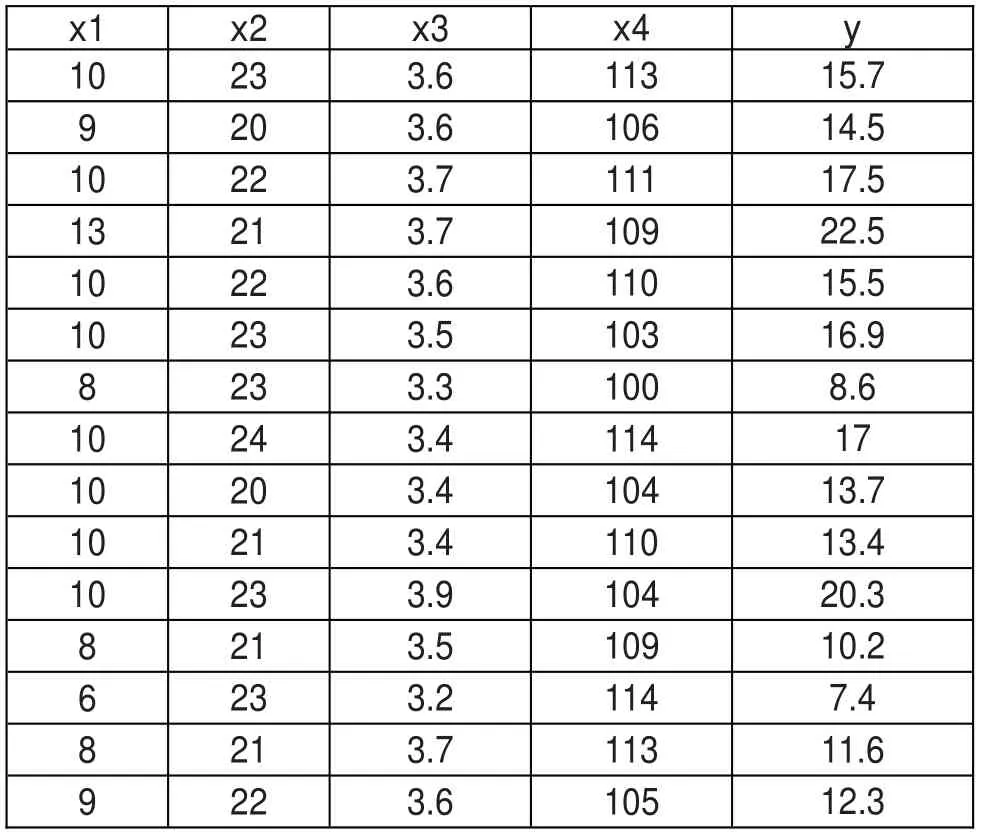
附錄1 路徑分析計算數據

import numpy asnp

import pandas as pd

from scipy.stats import f

df=pd.read_csv("pathdata.csv")#讀取文檔數據

y=df.iloc[:,-1]#得到y值

x=df.iloc[:,:-1]#得到x值

m,n=x.shape#得到x的行列數，為后期F檢驗做準備

r=df[["x1","x2","x3","x4"]].corr()#得到x1-4的相關系數

s=df.corr()["y"][:-1]#得到y對x1-4的相關系數

rni=np.linalg.inv(r)#得到相關系數R的逆矩陣

p=rni.dot(s)#得到直接相關系數

print(p)

a=np.diag(p)

P=r.dot(a)#得到直接、間接系數矩陣

P["sum"]=P.sum(axis=1)#得到直接、間接與總路徑系數矩陣（見表1）

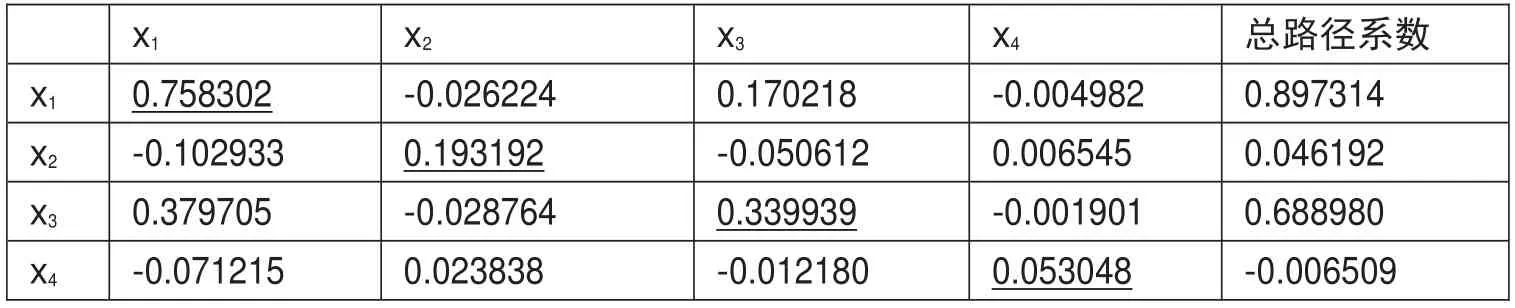
表1 直接、間接與總路徑系數

print("P",P)

del P["sum"]#刪除總路徑系數，為后期計算決定系數做準備

3 路徑系數的顯著性檢驗

3.1 F顯著性檢驗公式

由于路徑系數就是標準偏回歸系數，因而可以利用多元回歸分析中偏回歸系數顯著性檢驗的方法對路徑系數進行顯著性檢驗。檢驗方法可用t檢驗，也可用F檢驗。F值計算如下[15]：

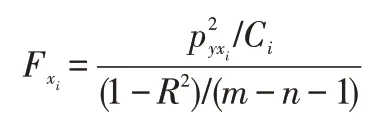
m為樣本容量，n為自變數個數。C是自變量相關系數的逆矩陣的主對角元素的倒數。

3.2 F顯著性檢驗Python實現

c=1/np.diag(rni)

fx=np.power(a,2).dot(c)/((1-r2)/(m-n-1))#計算數據F值

for iin fx:

print(i,f.sf(i,m-1,m*(n-1)))#利用第三方scipy.stats包做F檢驗(結果見表2)

表2 路徑系數F檢驗表

從表2可以得知，除X4路徑系數不顯著為0外，不拒絕零假設（H0），其它系數都達到顯著水平。認為路徑系數有意義。

4 決定系數的計算

4.1 決定系數的推導

決定系數(Coefficient of determination)R2表示y值的變異在其總變異中所占的比率。

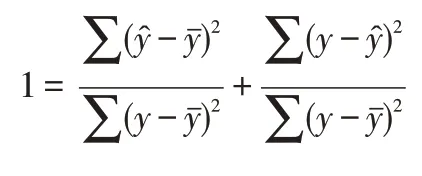
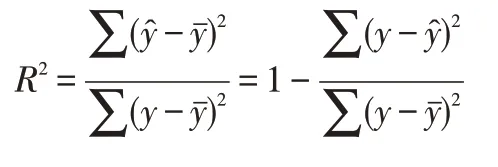
又因為

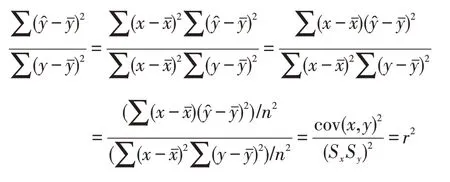
所以，決定系數是相關系數的平方。

在路徑分析中，根據因變量y的方差：

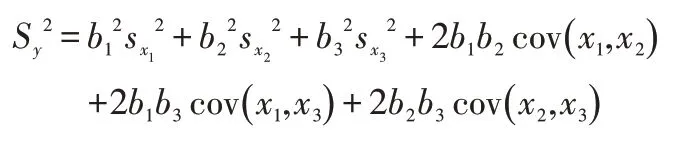
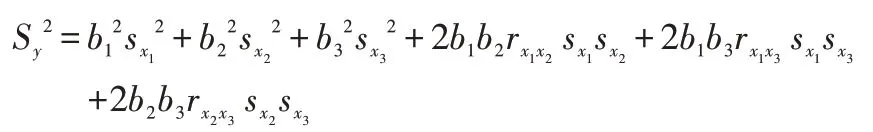
進一步推導：

表示自變量xi，對因變量y的相對決定程度，即直接決定系數；而2rxixj Pxiy Pxjy表示自變量xixj共同對因變量y的相對決定程度，即間接決定系數。總決定系數是直接決定系數與間接決定系數的和。為不可控因素e對因變量y的相對決定程度，稱為剩余決定系數。

4.2 利用矩陣計算決定系數

總決定系數R2=[1 1 1]*D*[1 1 1]T。則剩余決定系數pye2=1-R2。

4.3 決定系數Python實現

def toD(d):#封裝計算成D矩陣函數

5 路徑分析結果進一步探討

路徑分析的使用條件：各變量均為等距以上級別變量，各變量之間為線性關系，各因變量的作用可疊加。因果關系必須是單向，不得包括反饋環節[17]。根據路徑系數的計算結果，可以進行以下分析：按絕對值大小，說明每一路徑對因變量的作用的相對重要性[18]。如果路徑系數接近相關系數，則反映了變量之間的真實關系[19]。如果相關系數大于0，但路徑系數小于0，說明間接效應是相關的主要原因，直接作用是無效的，二者一定通過中介發生作用[20]。一般而言，相關分析僅蘊含著因果關系，但由于大多路徑分析，有時間的先后關系，路徑分析為此進一步驗證了因果關系[21]。