長短時記憶的風電機組故障預測系統

鄭修楷，曾憲文

（上海電機學院電子信息學院，上海 201306）

風力發電是一種新能源發電方式，在全球能源緊缺、環境污染嚴重的情況下，受到了世界各國的高度重視。我國風電設備通常建立在風力資源豐富的西北地區和東南、華北沿海地區，一旦發生停機事故，一方面維修復雜，另一方面根據實際情況，故障會造成3～8天的停機［1］，帶來巨大的經濟損失。考慮到風機設備的故障機理多為應力疲勞的累計，且應力負載的累計難以統計和建模，在實際運行維護過程中，往往槳距角發生明顯的異常后才進行緊急停機處理［2］。

故障預測技術通過監測設備的實時運行數據，在故障發生之前以一定概率對未來的設備運行狀態進行預估［3］，從而做好充分的準備工作，保證風電機組的平穩運行。目前，故障預測技術都是以數據為驅動，對歷史數據進行訓練，形成對未來運行狀態的評估。Zhang等［4］運用自組織神經網絡建立故障發展的描述變量，并對狀態變量進行跟蹤，從而預測軸承剩余壽命。馬玉峰［5］提出了一種小波神經網絡，利用傳感器檢測數據建立故障演變模型，預測軸承剩余壽命。但這些模型仍屬于淺層學習模型，風機運行時，各部件之間具有復雜的耦合關系，淺層學習模型很難表示出其中的關聯性。

深度學習憑借其強大的特征學習能力，已廣泛應用于圖像處理、語音識別等［6］各個領域，但目前在風電機組故障領域的應用較少。文獻［7］將長短時記憶（Long Short Term Memory，LSTM）網絡用于非結構化文本的故障分類。Wang等[8]利用LSTM進行航空發動機的故障檢測，保證發動機正常運行。風電設備各子部件之間相互關聯、耦合，使得數據存在空間上的關聯性，并且時序數據當前時刻值與歷史數據亦存在時間上的關聯性［9］，這與LSTM善于處理高維、強耦合、高度時間相關性數據的特點相吻合。由于風電機組發生故障是一個設備狀態逐漸演化的過程，具有強烈的時間特性，因此，提出了一種基于LSTM網絡的故障預測方法。通過上海電氣集團故障診斷平臺采集數據，驗證了該模型在故障隨時間序列演變過程中，能盡早地做出預測，且具有較高的精確度。

1 風電機組故障預測方法研究

傳統的前饋型神經網絡，輸入信號只能在相鄰信號源之間進行正向傳播，同層級的神經元之間沒有相互連接，因此不能發現數據在時間上的相關性［9］。而循環神經網絡（Recurrent Neural Network，RNN）在前饋型神經網絡同層級神經元之間引入反饋機制，不僅能使隱藏層神經元獲取輸入層的輸出信號，同時也能獲取來自其下一層的神經元反饋信號，使得神經網絡在處理數據時能獲取數據關于時間的相關性。

1.1 RNN

基本的RNN結構可看作同一層神經結構在時間序列方向上的連接，形成完整的神經網絡循環體，如圖1所示。圖中，x t為t時刻的輸入；yt為t時刻的輸出；st為t時刻的隱藏層狀態。神經網絡在計算輸出值yt時會將當前時刻的隱藏層狀態傳遞到下一時刻，從而表達數據在時序上的相關性。

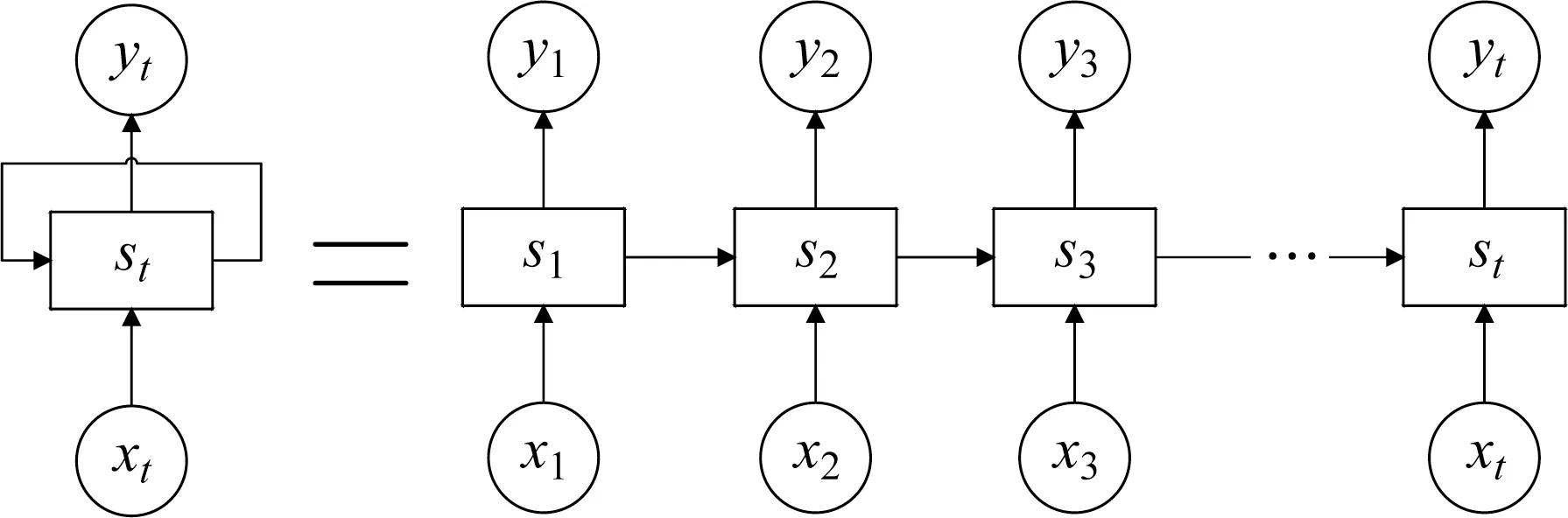
圖1 RNN模型圖

1.2 LSTM神經網絡

RNN的結構比較簡單，相鄰兩個時刻的神經元會相互共享隱藏層的信息，如圖2所示。但RNN在時間序列過長時很容易產生梯度爆炸和梯度消失的問題，導致在訓練時梯度的傳遞性不高［10］，即梯度不能在長序列中傳遞，使RNN無法檢測到長序列的影響。對LSTM神經網絡引入門控機制，提高了網絡的長期依賴能力，解決了RNN的梯度爆炸和梯度消失問題［11］。

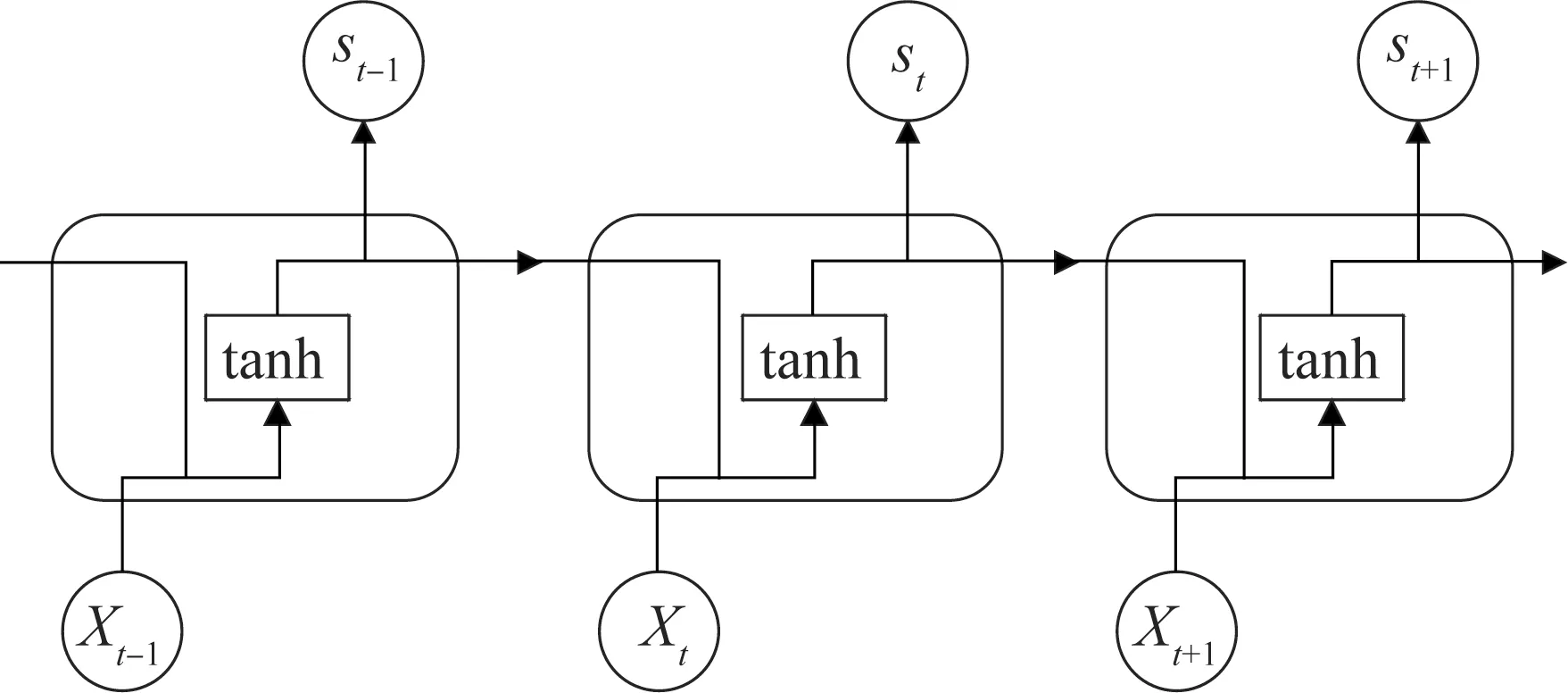
圖2 RNN結構

圖2中，tanh為RNN模型的激活函數，tanh的數學表達式為

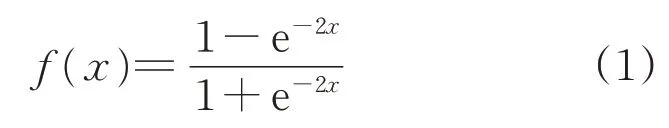
tanh將輸入數據歸算到[-1，1]之間，使RNN模型減少迭代次數。

LSTM模型訓練的關鍵是細胞狀態的更迭，ct表示細胞狀態的這條線水平地穿過圖的頂部。細胞的狀態類似于輸送帶，其在整個鏈上運行，只有一些小的線性操作，保持信息不變流過整個鏈［12］。而LSTM具有刪除或添加信息到細胞狀態的能力，這個能力是由被稱為門（Gates）的結構所賦予。門是一種可選地讓信息通過的方式。LSTM單元中，包含3種類型的門控，通過門控對信息存儲和更新，如圖3所示。

圖3 LSTM模型

門控分別為：輸入門、遺忘門和輸出門。每個門結構包含了一個以Sigmoid為激活函數的神經網絡結構，其輸出值（表示控制信息傳遞的比例）范圍為0～1。輸出值越小，信息傳遞的比例就越小，從而實現對歷史信息的選擇性遺忘。門控的一般形式可以表示為

其中，

式中：W為輸入向量的權重；b為輸入向量的偏置。

LSTM決定了上一步輸出結果st-1的丟失和遺忘。該決定由被稱為“遺忘門”的Sigmoid激活函數來實現。ft為“遺忘門”的門限，即歷史狀態ct-1被遺忘的比例，數學表達式為

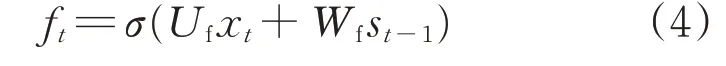
式中：Uf、Wf分別為當前輸入值x t和上一時刻記憶單元中輸出st-1對應的權重系數。

“遺忘門”決定了對上一時刻信息是否保留。當前輸出值為0時，前一時刻輸出值清除；輸出為1時，上一時刻輸出值保留。

“輸入門”決定了當前輸入值x t有多少被保留在ct之中，實現對狀態c的更新，其數學表達式為

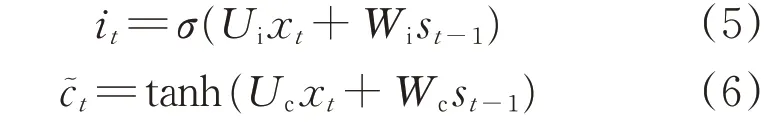
式中：it為經σ結構計算當前輸入x t與歷史輸入st-1后輸入數據被保留下來的比例；Ui、Wi分別為當前輸入x t與歷史輸入st-1的權重系數；c~t為當前時刻記憶單元所更新的狀態值；Uc、Wc為更新細胞狀態ct時刻輸入x t與歷史輸入st-1的權重系數。

“遺忘門”和“輸入門”可以實現對狀態c的刪除和更新。數據經過“遺忘門”與“輸入門”之后被保留下來的狀態數據如下：

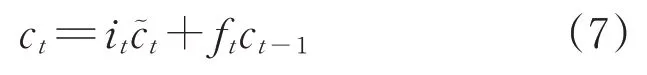
“輸出門”用來表示隱藏層的輸出，其數學表達式如下：

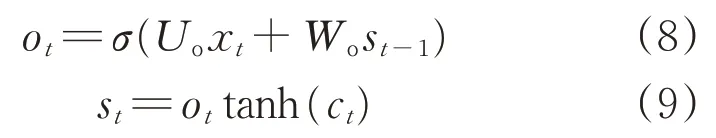
式中：ot為輸出門，決定當前記憶單元（cell）中的信息輸出程度，ot為0時表示數據完全不輸出，ot為1時表示數據完全輸出；Uo、Wo分別為x t、st-1的權重系數。

1.3 基于LSTM的故障預測流程

本文以風電機組的齒輪箱為例，基于LSTM建立故障預測的數學模型，流程如圖4所示。其中，包括對歷史數據的學習和實時數據的監測。通過經驗設定故障閾值，當模型計算數據超出閾值時，發出故障預警信號。

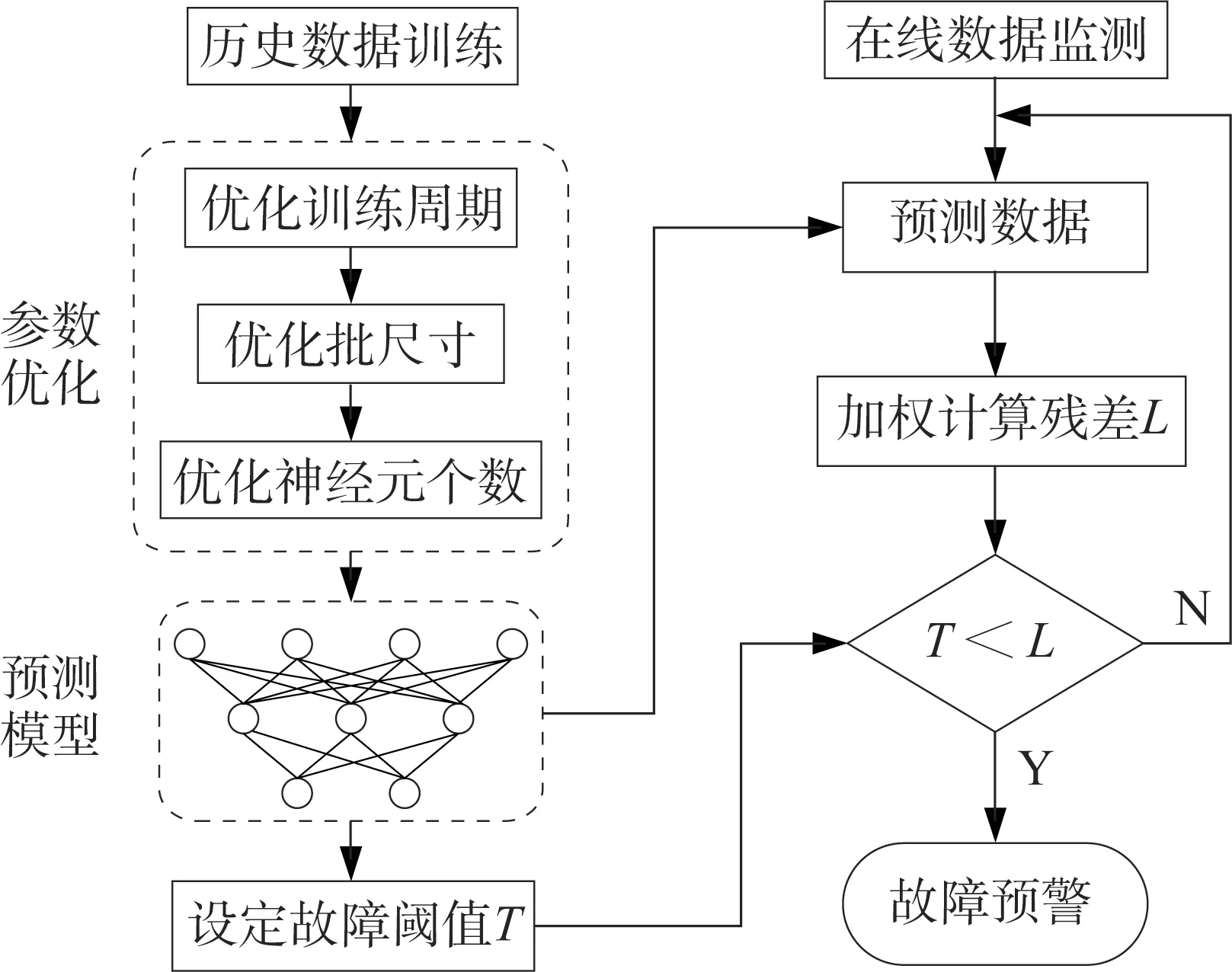
圖4 風電設備故障預測流程

1.3.1 模型構建本文以加速度傳感器采樣得到齒輪在正常、磨損狀況下的振動信號。由于輸入信號維度較多，因此選取輸入軸電機側軸承y1、輸出軸電機側軸承y2，檢測得到數據構造模型。模型的輸入為

1.3.2 模型參數優化在LSTM中，參數的選擇關系到整個模型的性能，其中超參數對模型的復雜性和學習能力起著決定性的作用。因此，對其進行優化能提高模型的學習能力和預測效果。優化參數如下：

（1）激活函數。激活函數能夠給神經網絡加入非線性因素，使得神經網絡可以更好地解決較為復雜的問題［13］。雖然普遍使用tanh激活函數，但在本模型中使用Softsign激活函數代替tanh函數，Softsign函數相比tanh函數，速度更快且不易飽和。Softsign函數公式為

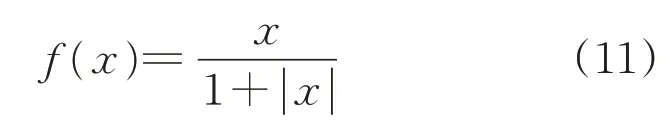
（2）訓練周期。一個訓練周期的定義是完整地遍歷數據集一次。在訓練中，一般應讓訓練持續多個訓練周期，并將迭代次數設為一次。一般僅對非常小的數據集進行完整批次的訓練時，才會采用大于1的迭代次數［14］。若訓練周期數量太少，網絡就沒有足夠的時間選取合適的參數；訓練周期數量太多則有可能導致網絡對訓練數據過擬合。

（3）批尺寸。批尺寸定義為一次訓練所選取的樣本數，其決定了訓練樣本每次訓練的樣本數量，代表控制更新網絡權重的頻率。

（4）正則化。正則化方法有助于避免在訓練時發生過擬合。Dropout是一種常見的正則化方法［15］，可以隨機地臨時選擇一些中間層的神經元，使這些神經在本次迭代中輸出為零，同時保持輸入層和輸出層的神經元數目不變。在反向傳播并更新參數的過程中，與這些節點相連的權值不需要更新。但是這些節點并不從網絡中刪除，并且保留其權值，使這些節點在下一次迭代時重新被選中，作為起始作用點參與權值的更新。

（5）網絡層數和隱藏層神經元個數。采用網格搜索的方法對網絡參數進行優化。對比訓練模型的輸出預測結果在不同模型層數、隱藏層神經元個數下的均方根值和損失后，選擇模型表現最優的參數值［16］。網絡參數如表1所示，模型設定了2層LSTM神經網絡，第1層記憶單元數為32個，第2層為16個。

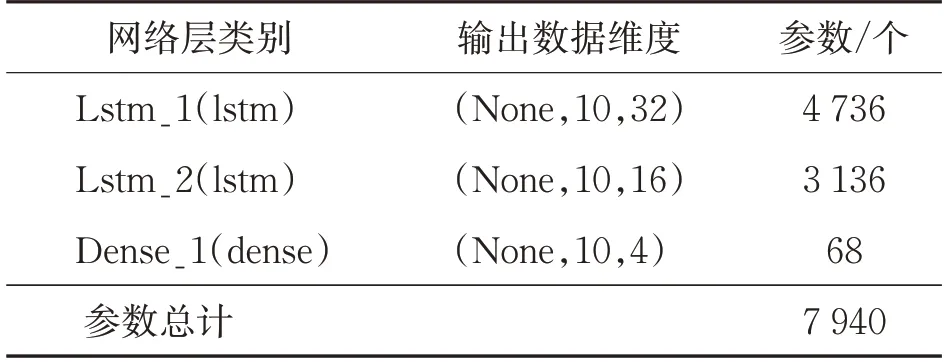
表1 網絡參數

（6）網格搜索法。網格搜索法作為一種常見的調參手段，是一種窮舉方法。給定一系列超參數，在所有超參數組合中窮舉遍歷，從所有組合中選出最優的一組超參數作為最優解。

2 故障預測方法的實驗驗證

2.1 實驗數據來源與分析

本文數據來源于上海電氣集團故障診斷平臺。實驗平臺由風機齒輪箱、變速驅動電機、軸承、傳感器、主軸等各部件組成，通過安裝、調試可模擬齒輪箱的各種故障。

選擇振動能量較為集中和突出的齒輪箱輸出端的軸承座作為測點位置，對輸入軸電機側軸承y1、輸出軸電機側軸承y2進行監測，獲取其振動加速度信號。實驗采用電火花加工技術在不同的齒輪上分別植入損傷點，模擬高速軸小齒輪齒面磨損和低速軸大齒輪斷齒所引起的故障狀態。設定采樣頻率為（2 000×2.56）Hz，利用加速度傳感器在轉速為1 470 r/min，加載電流為0.1 A時正常、磨損狀態下的振動信號，對信號進行預處理得到齒輪振動信號50組，每種狀態各25組。

2.2 故障狀態下的模型測試

對數據劃分后，使用驗證數據集在LSTM模型上進行故障預測，驗證數據集有5 771個數據。為了反映預測模型對于該數據預測的精確程度，數據在迭代訓練中的損失值如圖5所示。由圖可知，訓練集的損失在0～60次訓練中迅速下降，但稍有波動；在60～85次之間逐漸平緩，之后又出現波動。考慮到模型訓練耗時，以及在訓練過程中會出現過擬合的問題，選取訓練次數為80次。

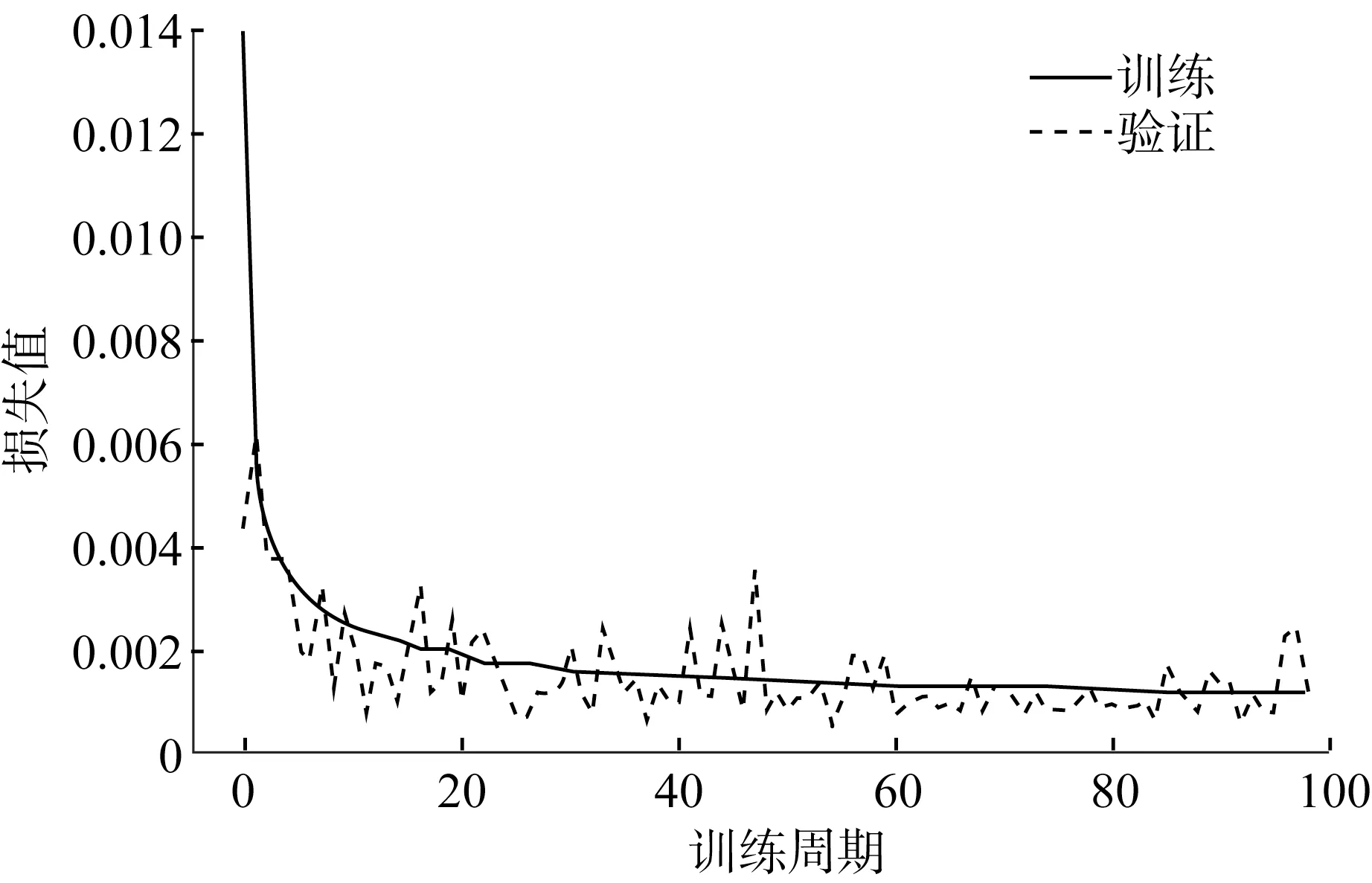
圖5 損失隨迭代次數變化曲線

根據經驗設定閾值（在齒輪故障中設定閾值T=0.2）之后，對比模型輸出預測值和真實值加權殘差，故障殘差預測結果如圖6所示。

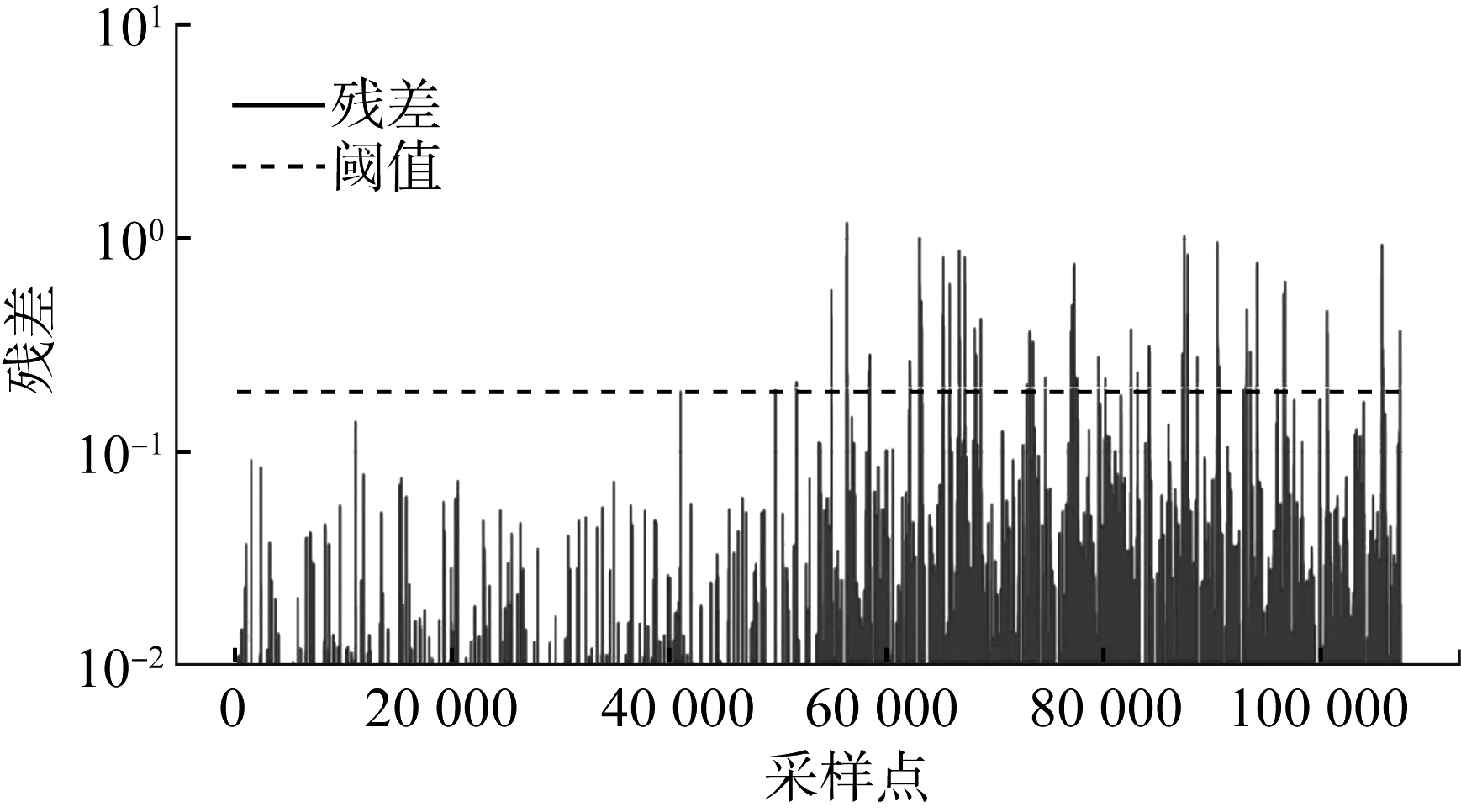
圖6 基于LSTM的故障預測結果

機組在正常運行狀態下其故障殘差很小，但故障狀態出現時數據殘差迅速增大，并且在隨后工作中殘差超出閾值線判定為故障，從而報警以利于盡早安排檢修以及供電計劃，避免故障的發生。

為了更好地反映LSTM模型的預測精確程度，迭代次數為80次時的預測結果分類混淆矩陣如圖7所示。混淆矩陣中，對角元素對應預測結果的精確度。由圖7可知，利用LSTM模型進行故障預測，預測結果具有較高的準確率。

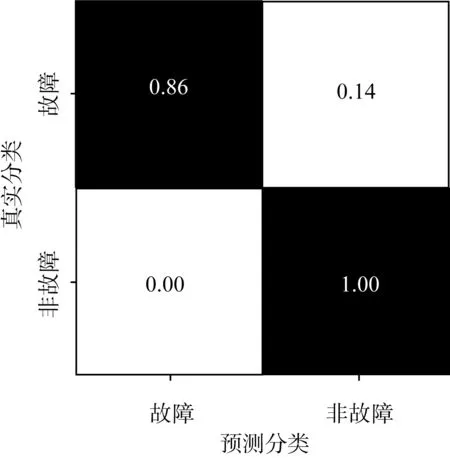
圖7 LSTM模型預測結果的混淆矩陣

3 結 語

本文針對風電機組運行時，各監測數據間耦合關系復雜的特點，提出以LSTM為模型的風電機組故障預測技術。首先，建立健康狀態下的LSTM模型；然后，根據其運行數據與預測數據進行對比計算得出殘差，當殘差超出閾值時，預測其發生故障。但在建立模型過程中，模型計算時間相對較長，可進一步優化隱藏層數與神經元個數，使預測準確率進一步提升，從而使模型能夠更快、更精確地預測出故障的發生，滿足風電正常生產運行的需要。