考慮行波效應(yīng)的大跨度懸索橋地震響應(yīng)分析

張世蒙 王貴春岳凱樂(lè)

（鄭州大學(xué)土木工程學(xué)院，鄭州 450001）

0 引 言

懸索橋是目前世界上廣泛采用的大跨徑橋梁，具有超強(qiáng)的跨越能力。懸索橋由于自身特性以及昂貴的維護(hù)費(fèi)用，成為健康檢測(cè)以及抗風(fēng)抗震研究的主要對(duì)象之一［1-2］。目前對(duì)橋梁進(jìn)行地震分析時(shí)，一致激勵(lì)是常用的分析方法，但由于懸索橋跨度一般較大，還需要考慮地震動(dòng)的空間效應(yīng)［3］。大跨度懸索橋?yàn)殚L(zhǎng)周期結(jié)構(gòu)，當(dāng)遇到大震或地震低頻成分豐富時(shí)，易發(fā)生共振導(dǎo)致橋梁破壞。所以對(duì)大跨度結(jié)構(gòu)進(jìn)行抗震研究時(shí)，長(zhǎng)周期地震作用下行波效應(yīng)的影響分析不容忽視［4-5］。

國(guó)內(nèi)外學(xué)者對(duì)該課題進(jìn)行了一系列的相關(guān)研究。Shehata E.Abdel Raheem等［6］以某一斜拉橋?yàn)槔芯苛说卣饎?dòng)空間效應(yīng)對(duì)斜拉橋地震響應(yīng)的影響，證明了考慮行波效應(yīng)的重要性。焦常科等［7］以泰州長(zhǎng)江大橋?yàn)槔M(jìn)行行波效應(yīng)分析發(fā)現(xiàn)：低視波速對(duì)結(jié)構(gòu)響應(yīng)的影響具有一定的震蕩性，并隨著視波速的增大趨于穩(wěn)定。閆聚考等［8］以泰州長(zhǎng)江大橋?yàn)槔?/40縮尺模型，進(jìn)行全振動(dòng)臺(tái)試驗(yàn)，研究在三種不同縱向約束條件下行波效應(yīng)對(duì)結(jié)構(gòu)響應(yīng)的影響，得出結(jié)論：行波效應(yīng)對(duì)結(jié)構(gòu)影響與結(jié)構(gòu)自身特性和地震動(dòng)特性密切相關(guān)，但文中所選視波速僅為低值，并沒(méi)有選高視波速進(jìn)行分析，也沒(méi)有與一致激勵(lì)結(jié)果進(jìn)行對(duì)比。丁幼亮等［9］以泰州大橋?yàn)槔x取了7條近斷層地震波、7條普通地震波進(jìn)行多塔懸索橋地震響應(yīng)對(duì)比分析，研究發(fā)現(xiàn)：在兩種不同地震作用下，地震響應(yīng)分布規(guī)律基本一致，受地震波自身特性和場(chǎng)地土的影響，峰值有所差別。文中雖對(duì)地震波進(jìn)行了討論，但未分析行波效應(yīng)的影響。目前，做懸索橋行波效應(yīng)研究時(shí)，大多數(shù)僅考慮了安評(píng)報(bào)告提供的加速度時(shí)程或一些常見(jiàn)的普通地震波。在近些年發(fā)生的地震中，長(zhǎng)周期地震動(dòng)對(duì)高層建筑以及大跨度橋梁造成的破壞更大，因此需要對(duì)其進(jìn)一步研究。

以潤(rùn)揚(yáng)長(zhǎng)江大橋?yàn)檠芯繉?duì)象，采用ANSYS有限元分析軟件，建立不考慮土-樁-結(jié)構(gòu)相互作用的懸索橋有限元模型。選取100～8000m/s范圍內(nèi)9組不同的視波速，采用時(shí)程分析方法，分析行波效應(yīng)對(duì)大跨度懸索橋地震響應(yīng)的影響，并探討了在普通地震動(dòng)、遠(yuǎn)場(chǎng)地震動(dòng)及近場(chǎng)地震動(dòng)作用下行波效應(yīng)對(duì)大跨度懸索橋地震響應(yīng)的影響。

1 工程概況

潤(rùn)揚(yáng)大橋?yàn)閱慰珉p鉸簡(jiǎn)支懸索橋，中跨跨徑為1 490 m，邊跨跨徑為470 m，在設(shè)計(jì)成橋狀態(tài)下，中跨主纜理論垂度為149.605 m，垂跨比約為1∶10，橋型圖如圖1所示。主梁為扁平流線型鋼箱梁，正交異性板橋面，梁高3 m，全寬38.7 m。主纜共兩根，中心距為34.3 m，吊索間距為16.1 m，其中近塔吊索距塔中心線20.5 m，為適度增強(qiáng)結(jié)構(gòu)縱向剛度，避免跨中短吊桿的彎折現(xiàn)象，在跨中設(shè)置剛性中央扣。索塔是由兩個(gè)塔柱、三道橫梁組成的門(mén)式框架結(jié)構(gòu)，塔柱為鋼筋混凝土空心箱形結(jié)構(gòu)，塔高210 m。

圖1 成橋狀態(tài)橋型總體布置圖Fig.1 General layout plan of bridge type

2 有限元模型及動(dòng)力特性

圖2為潤(rùn)揚(yáng)大橋的“脊骨梁式”空間有限元模型。橋面系、中央扣和主塔均采用空間梁?jiǎn)卧M，加勁梁按照吊桿的吊點(diǎn)進(jìn)行離散。加勁梁和吊桿采用剛臂連接。主纜和吊桿采用空間線性桿單元進(jìn)行模擬，主纜也按照吊桿的吊點(diǎn)進(jìn)行離散，單元受力模式為只受拉不受壓。下文簡(jiǎn)稱揚(yáng)州側(cè)主塔為北塔，鎮(zhèn)江側(cè)主塔為南塔。橋梁構(gòu)件截面特征和材料參數(shù)參照文獻(xiàn)［2］所設(shè)。

圖2 懸索橋有限元模型Fig.2 Finite element model of suspension bridge

所建模型對(duì)邊界條件的處理如下：在主梁梁端處耦合主梁和主塔的橫橋向、豎橋向以及繞順橋向的轉(zhuǎn)動(dòng)自由度；主纜和主塔頂部自由度全部耦合，不發(fā)生相對(duì)位移；邊纜底部以及主塔底部固結(jié)，不考慮樁土結(jié)構(gòu)相互作用。潤(rùn)揚(yáng)懸索橋有限元建模時(shí)采用的約束和邊界情況如表1所示。

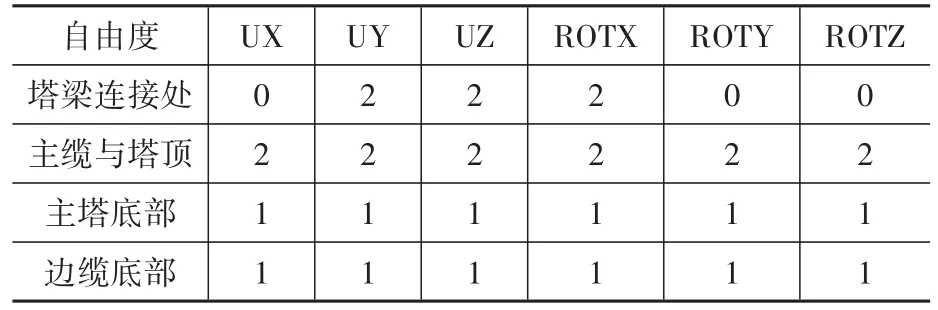
表1 模型約束及邊界條件Table 1 Model constraints and boundary conditions

模態(tài)分析是進(jìn)行抗震分析的基礎(chǔ)。采用Block Lanczos法對(duì)該大跨度懸索橋進(jìn)行模態(tài)分析，計(jì)算模態(tài)數(shù)為200階，表2僅展示前20階自振特性：該橋基頻為0.049 857 Hz，基本周期較長(zhǎng)，該橋的縱飄振型并沒(méi)有在前20階中出現(xiàn)，這主要是受剛性中央扣的影響。前20階主要以主纜和主梁的振動(dòng)為主，符合大跨度懸索橋這種柔性結(jié)構(gòu)體系動(dòng)力特征的一般規(guī)律。

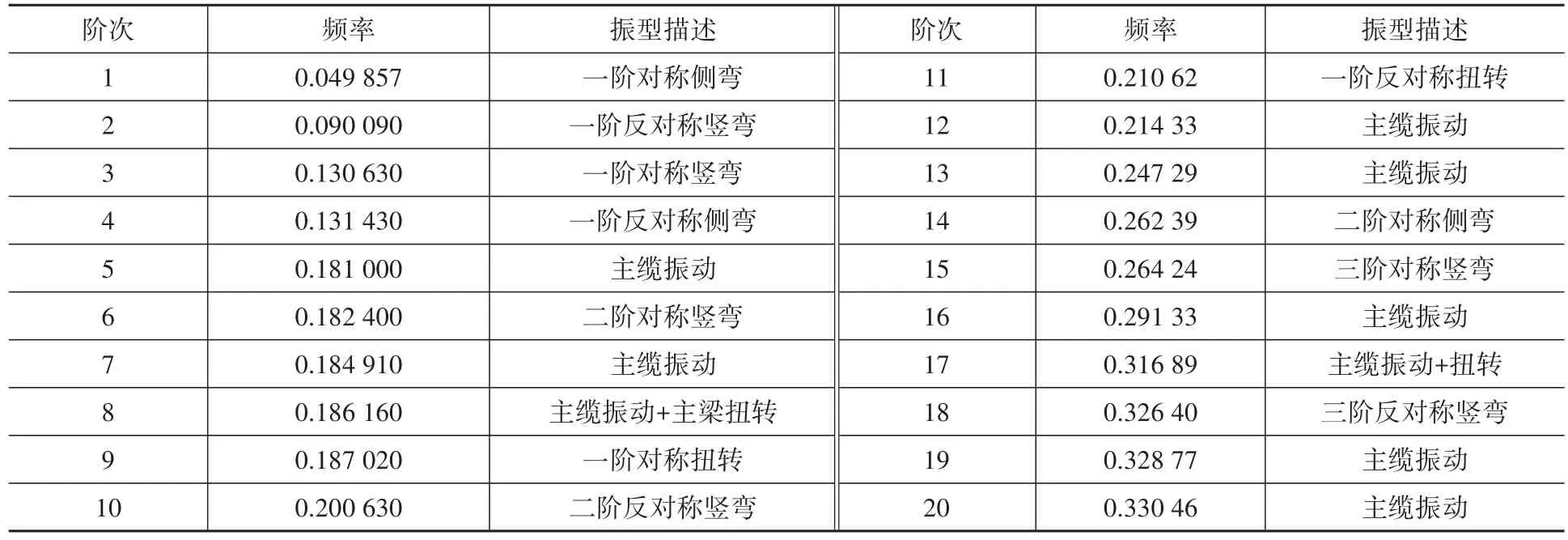
表2 動(dòng)力特性分析Table 2 Dynamic analysis of the suspension bridge characteristics

3 地震波

由于地震動(dòng)本身有很強(qiáng)的隨機(jī)性，不同的地震波有不同的震級(jí)、頻率、加速度峰值以及持時(shí)等［10］。根據(jù)《公路橋梁抗震設(shè)計(jì)細(xì)則》［11］（JTG/T B02-01—2008）規(guī)定，本文采用3條地震波進(jìn)行對(duì)比分析。其中包括El Centro波南北向，另外2條為遠(yuǎn)場(chǎng)地震波Chi-Chi-Taiwan CHY101（簡(jiǎn)稱CHY101）和近場(chǎng)脈沖型地震波Chi-Chi-Taiwan TCU102（簡(jiǎn)稱TCU102）。遠(yuǎn)場(chǎng)地震動(dòng)和近場(chǎng)地震動(dòng)均屬于長(zhǎng)周期地震動(dòng)，但兩者在孕育機(jī)制、頻譜特性等諸多方面都各不相同［12］，因此各選一條典型地震波進(jìn)行計(jì)算。圖3分別是3條地震波的加速度時(shí)程曲線。為防止在進(jìn)行行波效應(yīng)分析時(shí)位移時(shí)程發(fā)生縱飄現(xiàn)象，采用SeismoSignal軟件對(duì)地震波進(jìn)行基線調(diào)整［4，13］，保證地震波速度和位移時(shí)程曲線在地震波結(jié)束時(shí)回到零軸線。圖4以El Centro波為例給出SeismoSignal軟件對(duì)地震波進(jìn)行基線調(diào)整前后地震波速度和位移時(shí)程曲線的差異。

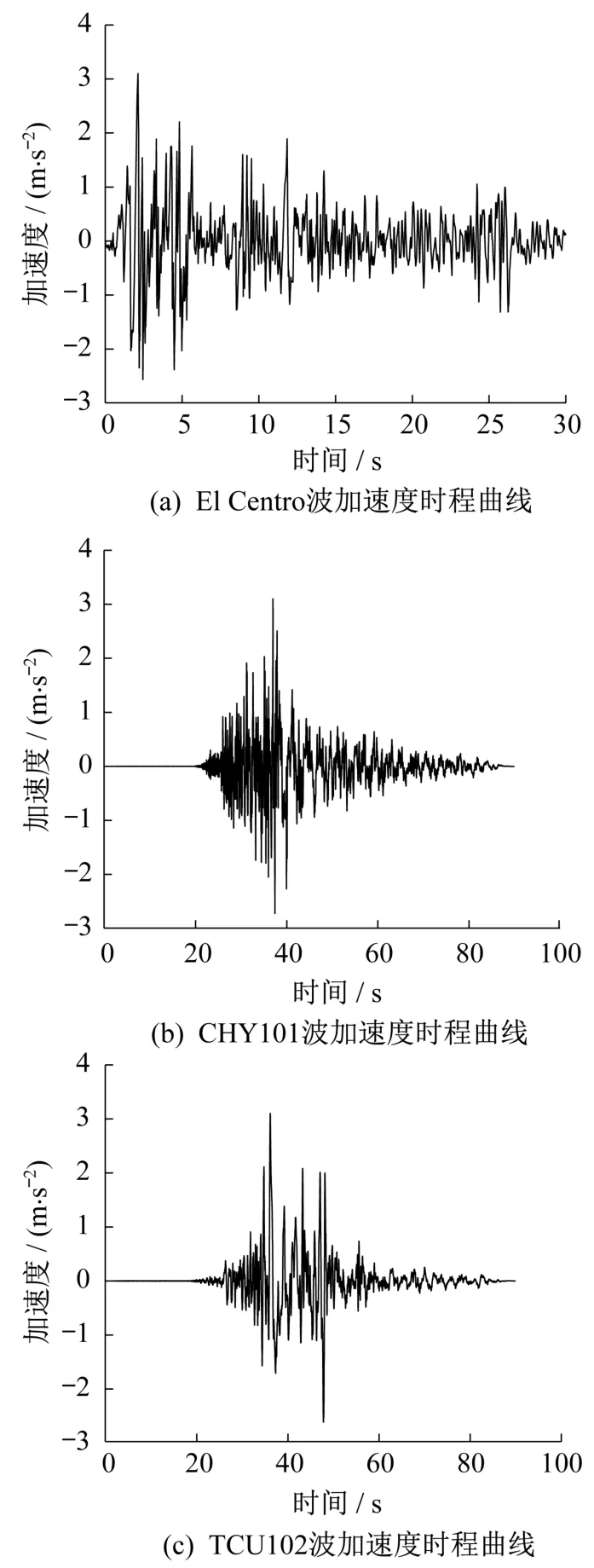
圖3 地震波加速度時(shí)程曲線Fig.3 Time-history curves of seismic wave acceleration

圖4 El Centro波經(jīng)調(diào)整后時(shí)程曲線差異對(duì)比Fig.4 Comparative differences of time-history curves of El Centro seismic wave

4 行波效應(yīng)分析

采用大質(zhì)量法對(duì)所建模型進(jìn)行行波效應(yīng)分析，地震波加速度峰值為0.3g。不考慮土-樁-結(jié)構(gòu)相互作用，阻尼比取0.01。所設(shè)大質(zhì)量為模型總質(zhì)量的106倍，以兩邊纜底部及兩主塔底部為地震波輸入點(diǎn)。做行波效應(yīng)分析時(shí)，視波速是懸索橋地震響應(yīng)的關(guān)鍵影響因素，本文所選視波速為100 m/s、200 m/s、500 m/s、1 000 m/s、1 500 m/s、2 000 m/s、4 000 m/s、6 000 m/s和 8 000 m/s，共 9組。地震波按照到達(dá)時(shí)間差輸入，如表3所列。圖5給出所采用的視波速與地震波持時(shí)之間的關(guān)系。

圖5 視波速對(duì)地震總持時(shí)的影響Fig.5 Effect of apparent wave velocity on total seismic duration

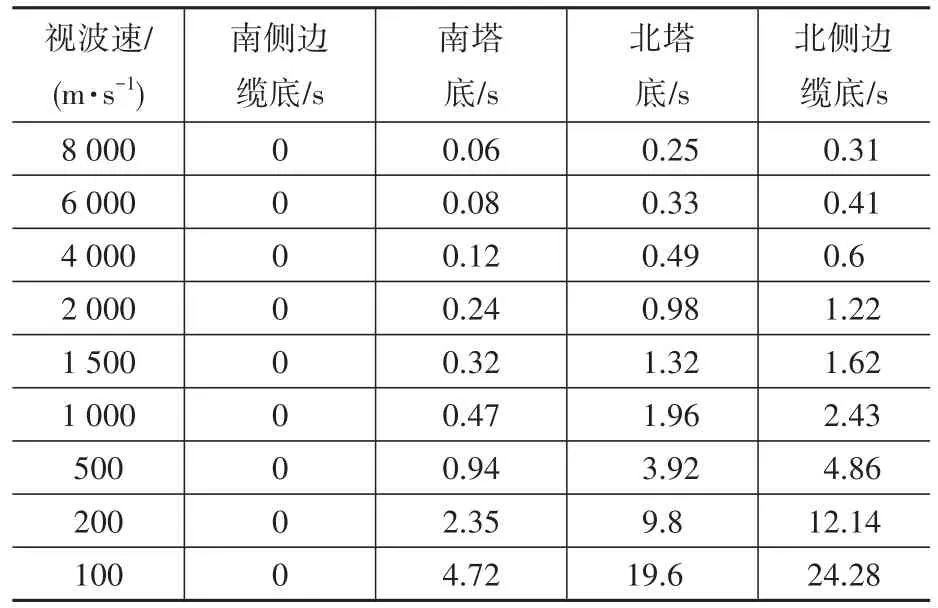
表3 行波效應(yīng)分析時(shí)不同視波速下對(duì)應(yīng)的時(shí)間差Table 3 Time interval at different apparent wave velocity when considering travelling wave effects

限于篇幅，圖6作僅給出在TCU102地震波作用下三組不同視波速的塔梁相對(duì)位移時(shí)程曲線。可以看出，視波速的不同會(huì)影響地震響應(yīng)的峰值以及地震總持時(shí)，視波速為100 m/s時(shí)，地震總持時(shí)明顯增加。以塔梁相對(duì)位移、塔頂順橋向位移、塔底橫向彎矩、塔底順橋向剪力為主要分析結(jié)果展開(kāi)討論。文中所述均為南塔以及主梁南側(cè)的地震響應(yīng)結(jié)果。

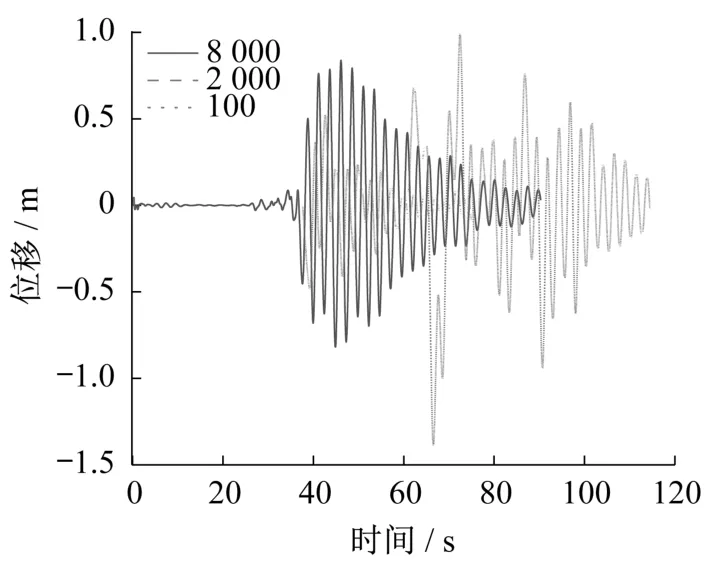
圖6 TCU102波輸入下塔梁相對(duì)位移時(shí)程曲線Fig.6 Time history curves of relative displacement between tower and beams input TCU102

圖7—圖10給出了在三種不同地震波作用下視波速為8 000 m/s時(shí)的地震響應(yīng)時(shí)程曲線。可以看出，近場(chǎng)地震TCU102波產(chǎn)生的地震響應(yīng)最大，遠(yuǎn)場(chǎng)地震CHY101波的次之，El Centro波作用下的對(duì)應(yīng)值最小。

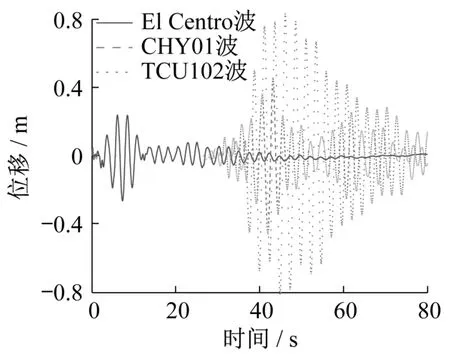
圖7 塔梁相對(duì)位移曲線Fig.7 Time history curves of relative displacement between tower and beams

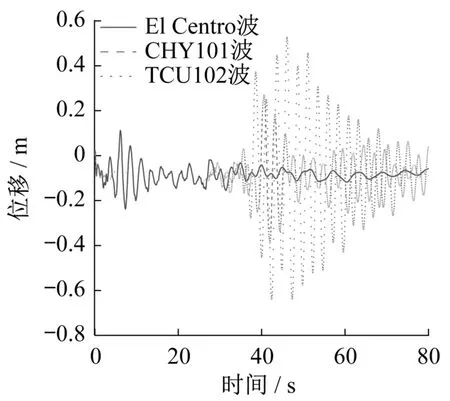
圖8 塔頂位移時(shí)程曲線Fig.8 Time history curves of displacement at tower top

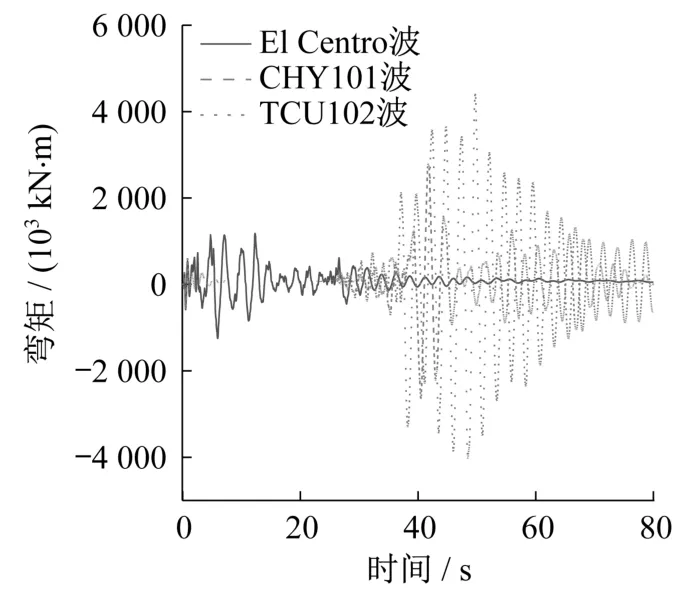
圖9 塔底彎矩時(shí)程曲線Fig.9 Time history curves of bending moment at tower bottom

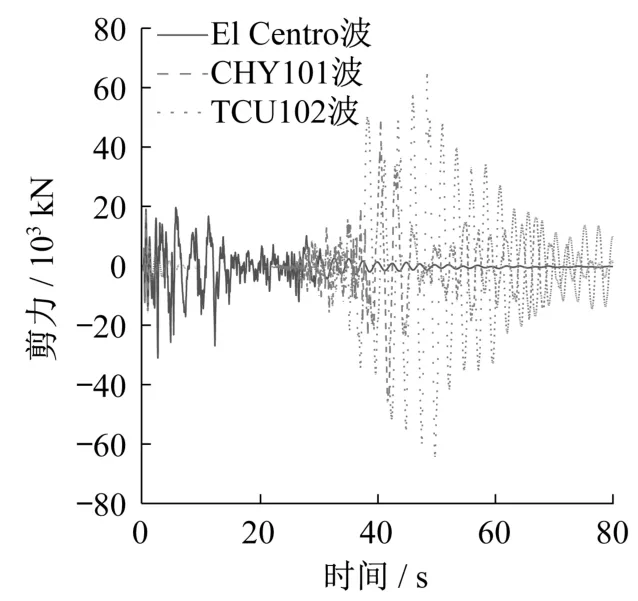
圖10 塔底剪力時(shí)程曲線Fig.10 Time history curves of shear force at tower bottom

在圖7中，近場(chǎng)脈沖型TCU102波作用下的塔梁相對(duì)位移峰值為0.838 1 m，是El Centro波輸入下對(duì)應(yīng)值的3.14倍；遠(yuǎn)場(chǎng)CHY101波作用時(shí)的對(duì)應(yīng)值為0.463 5 m，是El Centro波輸入下對(duì)應(yīng)值的1.73倍。

由圖8可以看出，近場(chǎng)脈沖型TCU102波作用下塔頂位移峰值為0.641 6 m，遠(yuǎn)場(chǎng)CHY101波作用時(shí)的對(duì)應(yīng)值為0.390 2 m，分別是El Centro波輸入下對(duì)應(yīng)值的2.7倍和1.64倍。

圖9顯示，El Centro波輸入下產(chǎn)生的塔底彎矩峰值為1 248 MN·m，比TCU102波作用下的對(duì)應(yīng)值小28.2%；圖10中塔底剪力峰值，TCU102波作用時(shí)較El Centro波作用時(shí)增加了1.62倍。產(chǎn)生上述現(xiàn)象的原因是，大跨度懸索橋?yàn)轱h浮的柔性結(jié)構(gòu)，自身阻尼較小，基頻較小，因此結(jié)構(gòu)響應(yīng)對(duì)地震波中的低頻成分更加敏感。

從圖11給出的功率譜密度曲線可以看出，El Centro波的卓越頻率為1.464 8，遠(yuǎn)場(chǎng)地震波CHY101的卓越頻率為0.336 7，近場(chǎng)脈沖型地震波TCU102的卓越頻率為0.408 9。對(duì)于大跨度懸索橋這種長(zhǎng)周期結(jié)構(gòu)，地震波卓越頻率與結(jié)構(gòu)頻率越接近，引起的地震響應(yīng)越大，當(dāng)?shù)卣鸩ǖ淖吭筋l率等于結(jié)構(gòu)頻率時(shí)，結(jié)構(gòu)的響應(yīng)最大［14］。近場(chǎng)脈沖型TCU102波的低頻成分更加豐富，且卓越頻率更接近于橋梁結(jié)構(gòu)基頻，因此產(chǎn)生的結(jié)構(gòu)地震響應(yīng)更大。

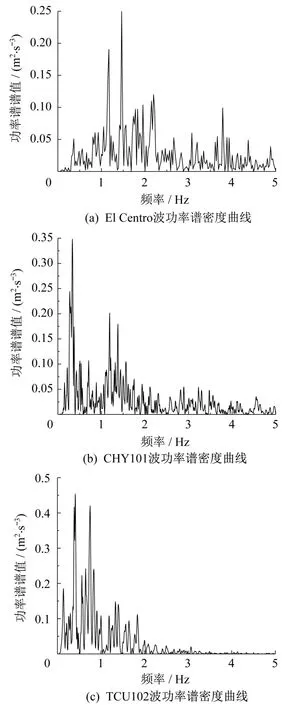
圖11 地震波功率譜密度曲線Fig.11 Wave power spectral density curve

圖12給出了三種地震波沿縱向輸入下，塔梁相對(duì)位移峰值隨視波速變化的關(guān)系。可以看出，在近場(chǎng)脈沖型TCU102波作用下，無(wú)論考慮行波效應(yīng)還是進(jìn)行一致激勵(lì)，所得塔梁相對(duì)位移峰值都是最大的，說(shuō)明大跨度懸索橋?qū)Φ皖l成分豐富的地震波更加敏感。當(dāng)視波速小于2 000 m/s時(shí)，三種地震波作用下塔梁相對(duì)位移峰值總體上呈現(xiàn)下降的趨勢(shì)；視波速大于2 000 m/s時(shí)，峰值逐漸增加并接近一致激勵(lì)的對(duì)應(yīng)值。考慮行波效應(yīng)時(shí)，TCU102波、CHY101波和El Centro波輸入下，塔梁相對(duì)位移峰值分別達(dá)到一致激勵(lì)對(duì)應(yīng)值的1.59倍、1.39倍和1.27倍。

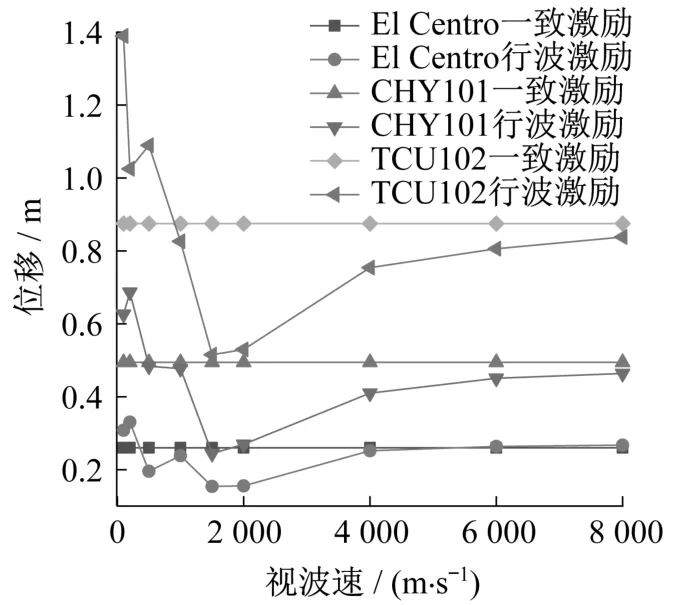
圖12 視波速對(duì)塔梁相對(duì)位移峰值的影響Fig.12 Effect of apparent wave velocity on the peak value of relative displacement between tower and beams

圖13給出了塔頂位移峰值隨視波速變化的趨勢(shì)。對(duì)比三種地震波所得結(jié)果可以看出，TCU102波作用下，塔頂位移峰值更大。視波速小于2 000 m/s時(shí)，響應(yīng)值有所波動(dòng)，在2 000 m/s之后，塔頂位移峰值呈現(xiàn)增加的趨勢(shì)并逐漸接近一致激勵(lì)的對(duì)應(yīng)值。

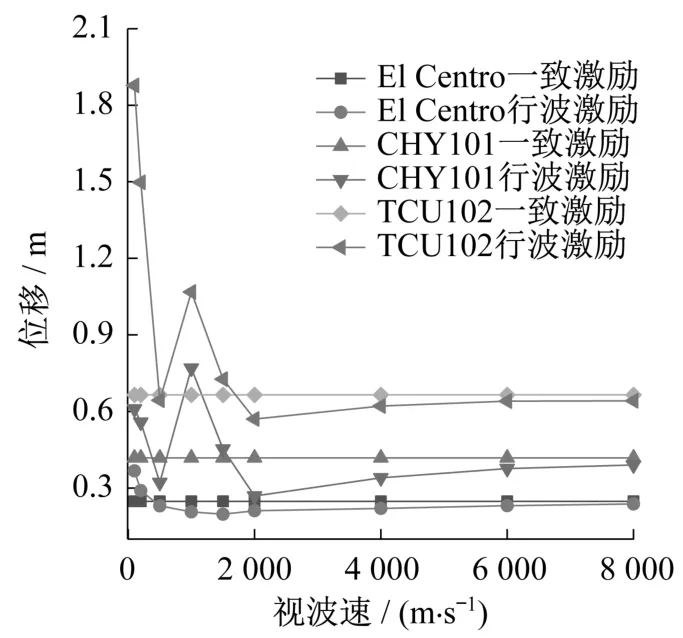
圖13 視波速對(duì)塔頂位移峰值的影響Fig.13 Effect of apparent wave velocity on peak displacement at tower top

在TCU102波輸入下，當(dāng)視波速為100 m/s時(shí)，塔頂位移峰值達(dá)到最大，為一致激勵(lì)對(duì)應(yīng)值的2.83倍。在CHY101波作用下，當(dāng)視波速為1 000 m/s時(shí)，塔頂位移峰值最大，為0.769 3 m，是一致激勵(lì)對(duì)應(yīng)值的1.84倍。在El Centro波作用下，當(dāng)視波速為100 m/s時(shí)，塔頂位移峰值達(dá)到最大值0.367 1 m，是一致激勵(lì)對(duì)應(yīng)值的1.48倍左右。

圖14為塔底彎矩峰值與視波速的變化關(guān)系圖。從圖中得出，近場(chǎng)脈沖型地震波TCU102作用時(shí)地震響應(yīng)更加顯著。在視波速小于2 000 m/s時(shí)，塔底彎矩峰值隨視波速的變化波動(dòng)較大，視波速大于2 000 m/s之后，可以明顯看出塔底彎矩峰值越來(lái)越接近一致激勵(lì)的對(duì)應(yīng)值。

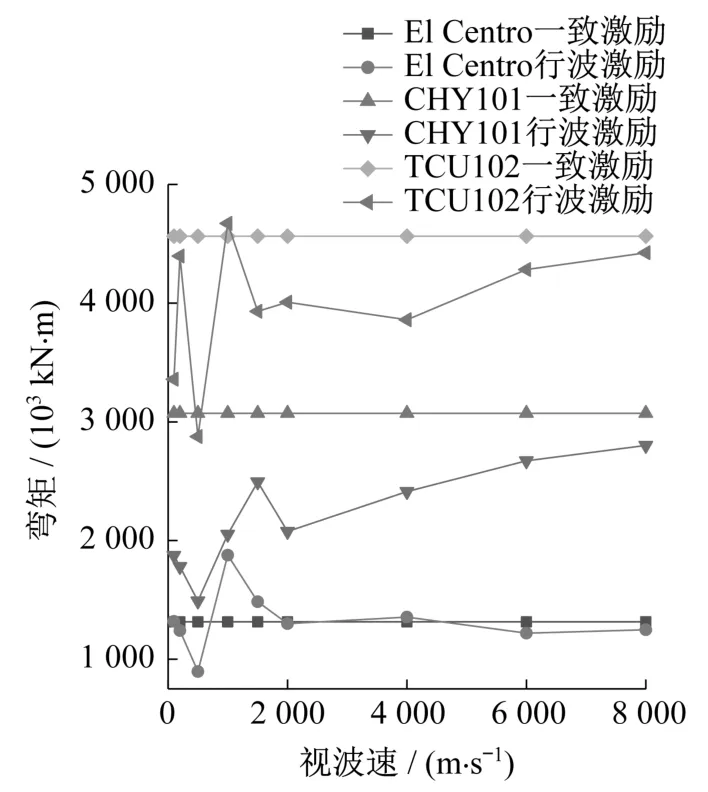
圖14 視波速對(duì)塔底彎矩峰值的影響Fig.14 Effect of apparent wave velocity on peak moment at tower bottom

在TCU102波輸入下，僅當(dāng)視波速為1 000 m/s時(shí)，塔底彎矩大于一致激勵(lì)的對(duì)應(yīng)值，為4 672 MN·m，其余視波速對(duì)應(yīng)的塔底彎矩峰值均小于一致激勵(lì)的對(duì)應(yīng)值，當(dāng)視波速為500 m/s時(shí)達(dá)到最小值，為2 875 MN·m。在CHY101波作用下，考慮視波速時(shí)所得塔底彎矩峰值均小于一致激勵(lì)的對(duì)應(yīng)值，當(dāng)視波速為500 m/s時(shí)，塔底彎矩峰值達(dá)到最小值1 490 MN·m。在El Centro波作用下，在所選視波速范圍內(nèi)，塔底彎矩峰值呈現(xiàn)先減小后增大再減小的趨勢(shì)，當(dāng)視波速為500 m/s時(shí)，其值最小，為896 MN·m；當(dāng)視波速為1 000 m/s時(shí)，其值最大，是一致激勵(lì)對(duì)應(yīng)值的1.43倍。從上述分析可以看出，當(dāng)視波速為500 m/s時(shí)，塔底彎矩值均最小。

圖15給出塔底剪力峰值隨視波速變化的關(guān)系。從圖中可以看出，在兩條長(zhǎng)周期地震波作用時(shí)，產(chǎn)生的塔底剪力峰值均小于一致激勵(lì)的對(duì)應(yīng)值，而在El Centro波作用下，考慮行波效應(yīng)時(shí)所得塔底剪力峰值基本均大于一致激勵(lì)的對(duì)應(yīng)值。在TCU102波作用下，當(dāng)視波速為100 m/s時(shí)，塔底剪力峰值最小，為48 MN；而一致激勵(lì)的對(duì)應(yīng)值為73 MN。在CHY101波輸入時(shí)，當(dāng)視波速取100 m/s時(shí)，塔底剪力峰值達(dá)到最小，為33 MN，而一致激勵(lì)的對(duì)應(yīng)值為52 MN。在El Centro波輸入下，當(dāng)視波速為1 000 m/s時(shí)，塔底剪力峰值最大為40 MN，是一致激勵(lì)對(duì)應(yīng)值的1.62倍。

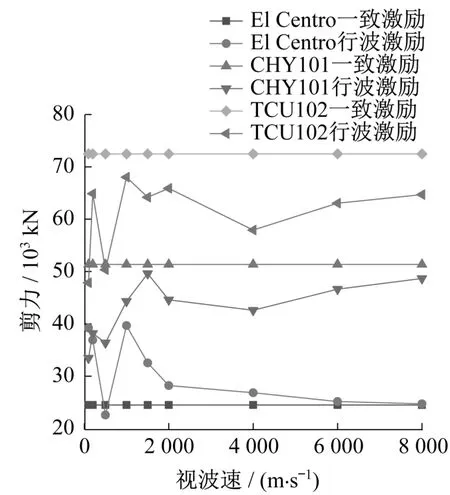
圖15 視波速對(duì)塔底剪力峰值的影響Fig.15 Effect of apparent wave velocity on peak shear force at tower bottom

在圖16中，以東南大學(xué)王春峰［15］所做泰州大橋?yàn)槔c本文潤(rùn)揚(yáng)大橋地震行波效應(yīng)分析對(duì)比，均采用El Centro波沿縱橋向輸入。可以看出：對(duì)于大跨度懸索橋，考慮行波效應(yīng)時(shí)，地震響應(yīng)峰值在低視波速區(qū)間內(nèi)波動(dòng)較大，隨著視波速增大，峰值逐漸接近一致激勵(lì)對(duì)應(yīng)值，驗(yàn)證了行波效應(yīng)分析的正確性。低視波速區(qū)間內(nèi)波動(dòng)較大的現(xiàn)象說(shuō)明抗震分析時(shí)考慮行波效應(yīng)的必要性，并且僅選一種視波速進(jìn)行分析是不科學(xué)的，需要選擇多組合適的視波速進(jìn)行分析，使結(jié)果具有普遍性。從圖中可以看出，不同的橋梁得到的峰值曲線圖不同，說(shuō)明行波效應(yīng)的影響與橋梁自身特性也有關(guān)系。

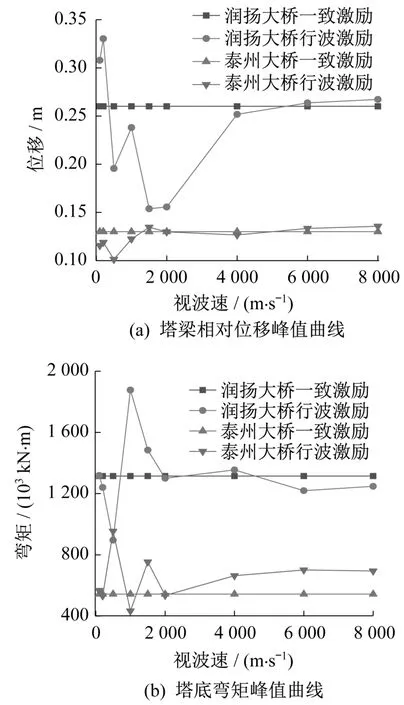
圖16 不同懸索橋地震響應(yīng)對(duì)比圖Fig.16 Comparison of seismic response of different suspension bridges

5 結(jié) 論

（1）采用近場(chǎng)脈沖型地震波Chi-Chi-Taiwan TCU102得到的懸索橋地震響應(yīng)最為顯著，其次為遠(yuǎn)場(chǎng)地震波Chi-Chi-Taiwan CHY101作用下的地震響應(yīng)，El Centro波作用下的對(duì)應(yīng)值最小。近場(chǎng)脈沖型TCU102波的低頻成分更加豐富，且卓越頻率更接近結(jié)構(gòu)基頻，地震響應(yīng)更大。

（2）對(duì)比一致激勵(lì)分析，行波效應(yīng)對(duì)懸索橋的地震響應(yīng)影響較大。在低視波速區(qū)間內(nèi)，塔梁相對(duì)位移最高達(dá)到一致激勵(lì)對(duì)應(yīng)值的1.59倍，塔頂位移最高為一致激勵(lì)對(duì)應(yīng)值得2.83倍。但在高視波速區(qū)間內(nèi)，視波速的影響明顯減低，位移峰值小于一致激勵(lì)的對(duì)應(yīng)值，并開(kāi)始逐步接近一致激勵(lì)的位移峰值，驗(yàn)證了行波效應(yīng)計(jì)算結(jié)果的正確性。

（3）輸入不同地震波時(shí)，行波效應(yīng)的影響也不相同。塔底內(nèi)力峰值，隨視波速的增大逐漸接近一致激勵(lì)對(duì)應(yīng)值；但在低視波速區(qū)間內(nèi)，內(nèi)力峰值波動(dòng)較大。

（4）對(duì)于類似大跨度懸索橋這種長(zhǎng)周期柔性結(jié)構(gòu)的設(shè)計(jì)，應(yīng)充分考慮行波效應(yīng)的影響。在抗震計(jì)算時(shí)，也要充分考慮低頻成分較為豐富的一類地震波對(duì)橋梁地震響應(yīng)的影響。行波效應(yīng)對(duì)結(jié)構(gòu)地震響應(yīng)的影響與結(jié)構(gòu)自身特性及地震波特性均有關(guān)系，所以在分析時(shí)，要正確建模、合理選擇地震波。