逆反射系數動態測試中的坐標系建立方法研究

李丹，楊燁，吳關，孫夢如，齊慕予

[交科院檢測技術（北京）有限公司，北京 100013]

0 引言

逆反射是反射光線從接近入射光線的反方向返回的一種反射。利用這一特性制作的逆反射材料，可有效解決交通安全設施的夜間視認問題[1]。由于逆反射材料是把光源照射的光線，通過材料表面的微觀結構反射回光源處[2]，其反射效果與入射角度、材料特性等因素有著密切聯系。同時，人眼對于光線的感受也存在著差異[3]。國際上，為了科學地表現這種光度性能的差異，研究人員總結出了逆反射系數（coefficient of retroreflection）[4]，1982年國際照明委員會（International Commission on illumination）首先對其做出了定義[5]。

逆反射系數作為交通安全設施的一項重要檢測指標，其測試結果對保障行車安全、提高道路通行效率具有重要意義[6]。根據測試原理的不同，逆反射系數的測試方法主要分為相對測量法和絕對測量法兩種[7]。相對測量法可以在一定的限度內用光度裝置縮短測試距離，其量值傳遞依賴于參考標準物質的標準值[8]。羅語丹[9]通過實驗比對不同檢測機構使用相對測量法的測試數據，結果顯示，在實驗環境可控的條件下，測試結果具有一定的可靠性。趙蓓俊[10]研究了一種基于相對測量法的儀器測試模型，通過重復試驗，驗證了數據的一致性，但是在可溯源性方面存在缺陷。SAMETOGLU[11]搭建了由計算機控制的相對測量法測試系統，可實現異常數據的自動剔除，但在準確性方面依然存在問題。因此，基于相對測量法的逆反射系數測試方法，無法保證測試數據的準確性、有效性和可溯源性，難以實現對逆反射系數的動態測試[12][13]。而絕對測量法是依據基本的光學傳感器，測量角度和距離可以溯源，具有更高的計量學特性[14]。MUZETV[15]通過分析標線逆反射特性，研究出一種基于絕對測量法的標線逆反射系數測試裝置，可實現固定角度的逆反射系數測量。GUTIERREZJA[16]通過研究駕駛員對交通標志的感知效果，建立了基于絕對測量法的測試系統。王義旭[17]等對比了逆反射材料在不同入射角、觀測角下逆反射系數測試數據，建立了測量角度與逆反射系數測關聯模型。當前，國內外尚無統一的逆反射系數動態測試方法，由于測量的幾何系統的建立方式不同，導致了測試結果的差異。

本文通過深入研究CIE54.2 RETROREFLECTION:DEFINITION AND MEASUREMENT中的逆反射測試理論，基于絕對測量法的實驗原理，分析逆反射系數動態測試中測量設備與待測物的三維空間關系。通過研究逆反射動態測量相關設備在道路檢測中的運動狀態，建立包含測量角度、測量距離等關鍵因素的數學模型，為相關逆反射動態測試的研究提供理論基礎。

1 逆反射系數測試概述

1.1 測試原理及設備

逆反射系數測試是對逆反射材料光度性能進行科學定量分析和產品質量控制的重要手段。目前我國交通安全設施逆反射系數的測試方法，主要采用《逆反射系數測試方法 共平面幾何法》（JT/T689—2007）中規定的共平面幾何法[18]，搭建靜態的角度系統，其測量原理如圖1所示。

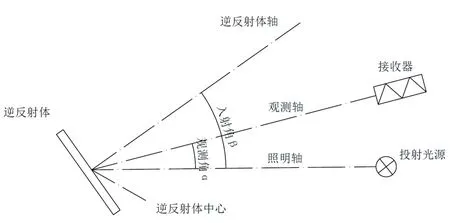
圖1 共平面幾何法測量原理

測試光線由光源發出，沿照明軸射向逆反射體，其反射光線沿觀測軸射向接收器。觀測軸、照射軸和逆反射體軸共同構成了測試幾何系統。其中，觀測角α為照明軸與觀測軸之間的夾角，觀測角不為負值，一般小于10°，通常小于2°；入射角β為照明軸和逆反射體軸之間的夾角，入射角通常不大于90°，但考慮完整性將其規定為0°≤β≤180°。逆反射體軸是指從逆反射體中心發出的一條假想的射線，一般垂直于逆反射體表面。

依據逆反射系數靜態測試原理和測量的可溯源性要求，逆反射動態測量設備主要由投射光源、接收器、角度控制結構組成。對于逆反射系數的測試過程，確定測量角度是提高測試數據準確性的關鍵。而交通工程設施逆反射系數的測量，往往由于待測逆反射體位置的不固定，無法建立準確的測量幾何關系，而導致測量誤差的出現。

1.2 測試的角度系統

實際道路檢測時，測量設備與待測逆反射體的相對位置不固定，需要建立三維空間關系才能確定測量的角度是否滿足要求。按照不同測試環境和待測樣品的固定方式，CIE54.2中共有以下四個系統（圖2）：（1）{α、β1、β2、ε}CIE角度系統；（2）{α、β、γ、ωs}固有系統；（3）{α、β、ε、ωs}應用系統；（4）{a、b、e、d}標線系統。

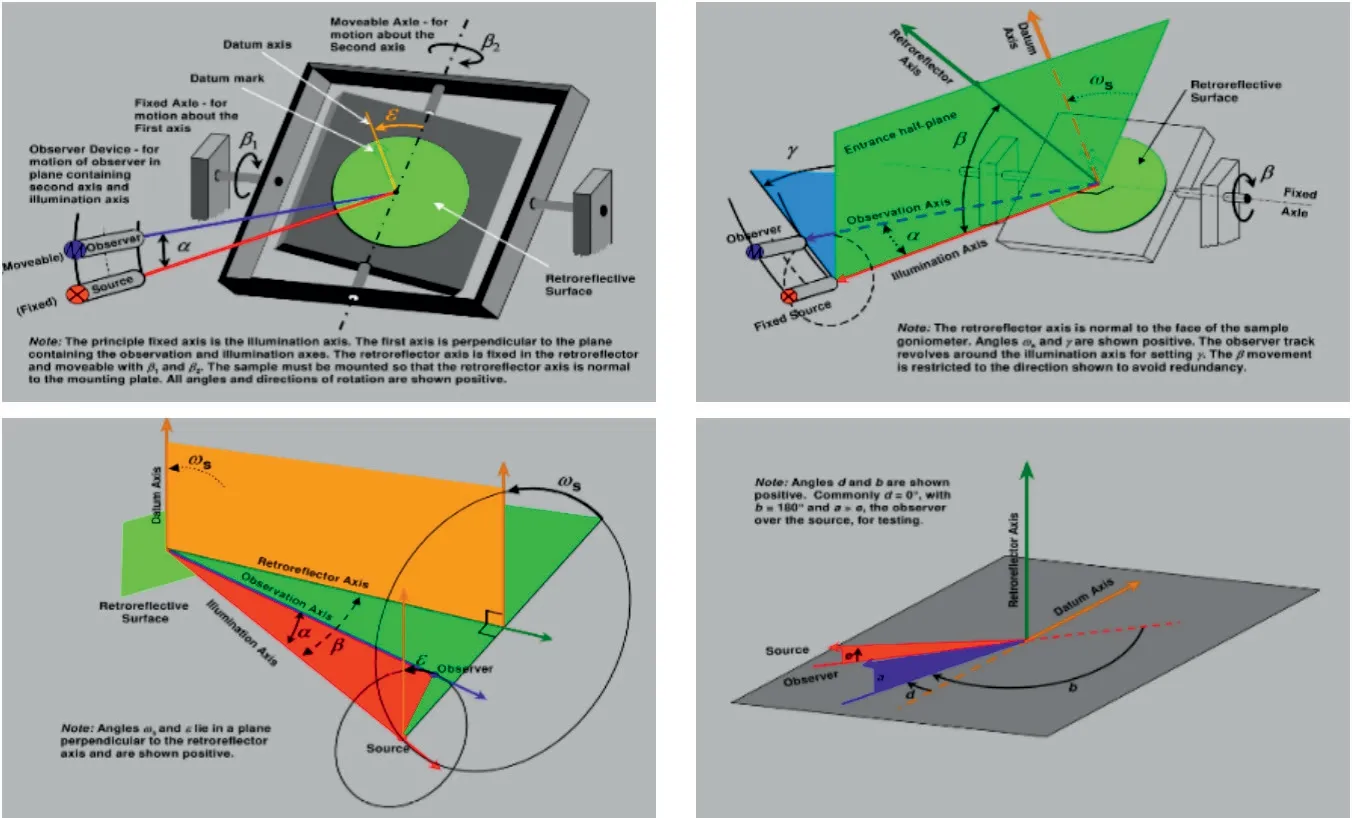
圖2 逆反射測量角度系統（圖片來源：CIE54.2）

這四個系統展示了逆反射體在三維空間不同姿態時的測試方法，值得注意的是，其中接收器及光源的相對固定，觀測角α的大小可通過調整投射光源與接收器的間距來改變，而由于待測試逆反射體的空間位置的不固定，入射角β的變化范圍較大。因此，逆反射系數動態測試的幾何系統可由多個變量簡化為單一變量控制，即入射角β的角度控制。

2 數學模型的建立

2.1 測試場景分析

在實際道路檢測中，交通安全設施由于功能定位不同，其設置位置、角度等都存在較大差異。以交通標志為例，《道路交通標志和標線 第2部分：道路交通標志》（GB 5768.2—2009）規定了多種交通標志類型[19]。

車載逆反射系數測試系統由逆反射動態測量設備和載具構成，測量設備安裝在載具頂部。根據《道路交通反光膜》（GB/T 18833—2012）標準要求，交通標志逆反射系數的測量角度應滿足α=0.2°，β=-4°[20]。通過調整設備姿態，在三維空間的某一平面內建立測量的角度關系（如圖3所示）。系統在達到逆反射系數測試的角度要求的測量距離時進行測量。根據該測試模型，逆反射系數動態測試的角度可由待測物位置和測量距離計算得出。

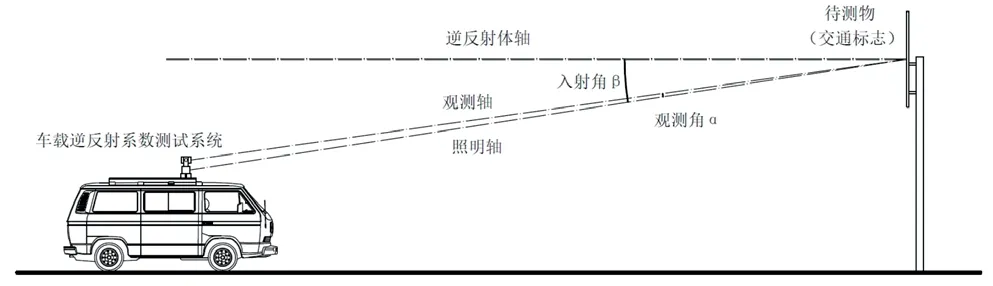
圖3 交通標志逆反射動態測試場景示意圖

根據道路條件，以及逆反射系數動態測試的角度要求，逆反射系數測試設備的姿態調整過程主要由平動i=(x,y,z)T和轉動t=(ω,θ,ψ)T兩個部分組成，符合剛體一般運動的特點，s=(x,y,z,ω,θ,ψ)T。由此，逆反射系數動態測試中的角度控制問題，可以轉化為逆反射系數動態測量設備在三維空間的運動問題。通過建立合理的坐標系，建立與待測物的角度計算關系，指導設備進行姿態調整。

2.2 整體坐標系

整體坐標系是測試幾何系統的基礎。采用笛卡爾直角坐標系，建立空間的點與有序數組關聯的數學模型。結合道路檢測場景，建立逆反射系統動態測試的整體坐標系如下：坐標系原點為測試設備在路面的投影點，設為O點，道路所在平面為坐標系的x-y平面，假設x與行車方向相反，y軸垂直于x軸并指向路肩，z軸通過原點并垂直于x-y平面，以路面上方為正方向。由此，道路檢測直角坐標系Oxyz如圖4所示。

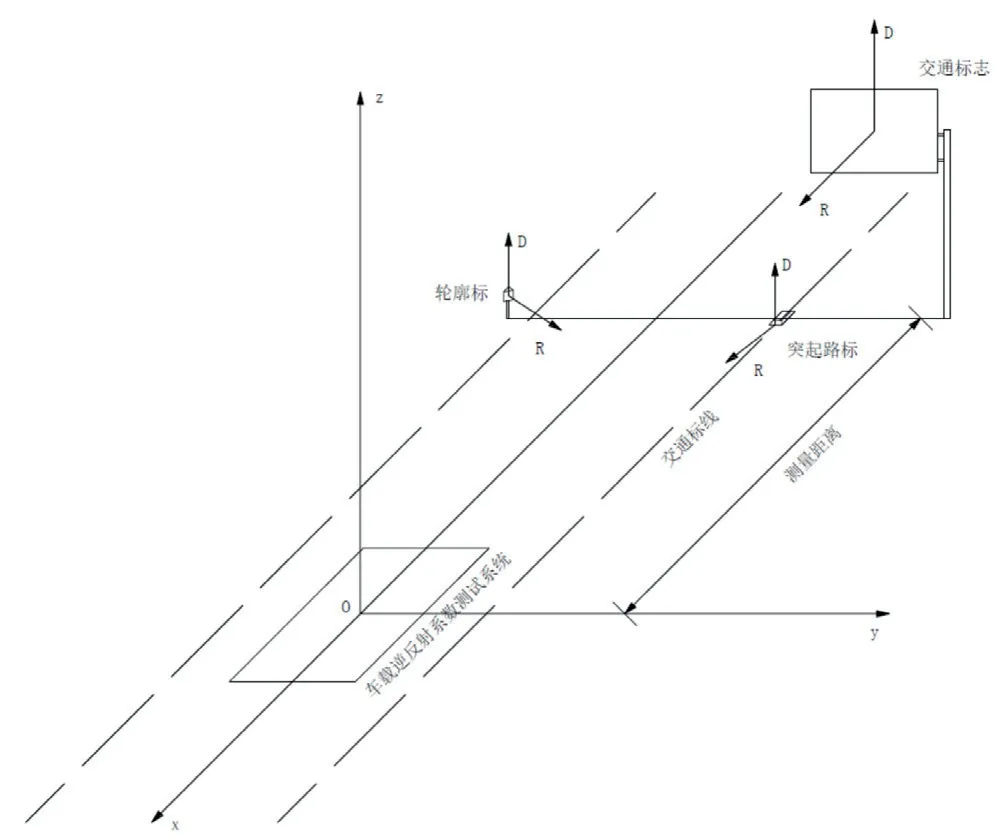
圖4 道路檢測直角坐標系示意圖

根據逆反射系數的測試原理，整體坐標系中的空間點可轉化為向量關系。出于控制變量及模型化考慮，在本文建立的道路檢測模型中，待測物均為理想狀態檢測目標。在逆反射系數動態測試的整體坐標系中，假設待測物的逆反射體軸均可與某一條或多條坐標軸建立垂直或平行關系。基準軸通過逆反射體表面，并與路面所在平面垂直，用于待測物在x-y平面的定位。照明軸由測試光源發出，指向待測逆反射體，測試光源的高度Z在測試系統中相對固定。觀測軸由逆反射系數測試的接受器發出，指向待測逆反射體。由此，得出以下四條逆反射測試空間的向量，如表1。

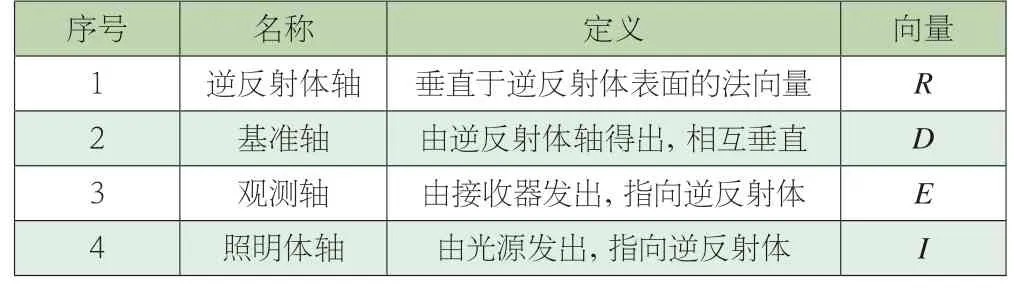
表1 逆反射測試空間的構成向量

在直角坐標系中的表示如下：

根據向量運算法則，可推出測量的觀測角α、入射角β的計算方式如下：

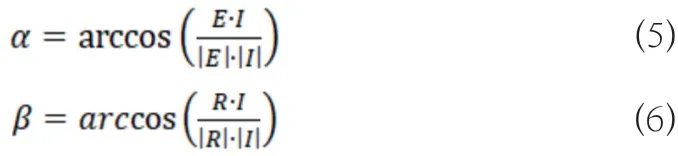
2.3 局部坐標系

上述整體坐標系，建立了測量角度與測量距離的函數關系，但無法解決測試設備的姿態調整問題，即剛體的轉動。因此，需要引入歐拉角，建立測試設備的局部坐標系。歐拉角是用來唯一地確定定點轉動剛體位置的三個一組獨立角參量，由章動角θ、進動角ψ和自轉角φ組成。

假設測試設備的姿態調整為剛體運動，在以原點為O的直角坐標系Oxyz基礎上，建立剛體的坐標系Ox‘y‘z‘。以軸Oz和Oz‘為基本軸，其垂直面Oxy和Ox‘y‘為基本平面。由軸Oz量到Oz‘的角度θ稱為章動角。平面zOz‘的垂線ON稱為節線，它又是基本平面Ox‘y‘和Oxy的交線。在右手坐標系中，由ON的正端看，角θ應按逆時針方向計量。由固定軸Ox量到節線ON的角度ψ稱為進動角，由節線ON量到動軸Ox‘的角度φ稱為自轉角。測試設備的局部坐標系如圖5所示。

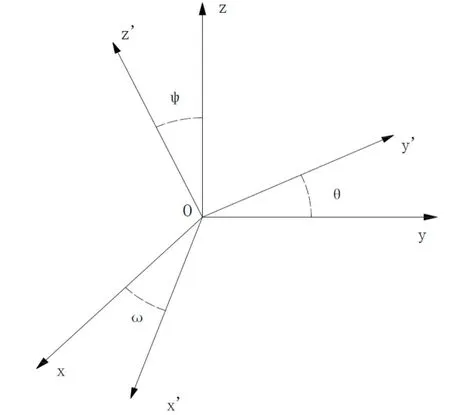
圖5 逆反射測試設備局部坐標系

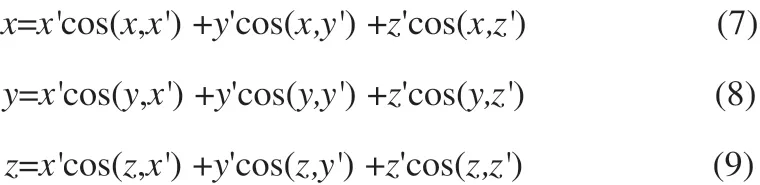
上述三個旋轉雖然在三維笛卡爾直角坐標系下進行，但都是平面旋轉，他們的旋轉矩陣分別是:

根據姿態調整的順序，則從直角坐標坐標系到局部坐標系的歐拉轉換矩陣是：

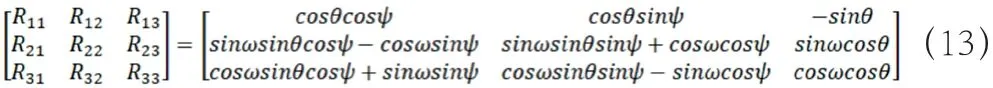
在已知轉換矩陣的條件下，可推出姿態角的計算方式：

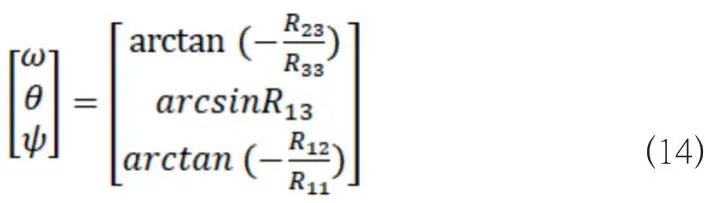
由此，可得出在直角坐標系中確定測量距離、測量角度的前提下，調整測試設備姿態的方法。

3 結語

本文在絕對測量法的基礎上，從逆反射系統動態測試的原理及設備、使用場景等方面對逆反射系數測試方法展開研究，首次提出了逆反射系統動態測試整體坐標系的建立方式，解決了逆反射系數動態測試中的測量角度、測量距離計算等問題。并引入歐拉角，建立以測量設備為中心的局部坐標系，給出了測試三維空間的角度轉換關系，為測量設備的姿態調整提供了計算方法，可為相關逆反射動態測試的方法研究及相關設備的研發提供參考。在后續的工作中，將繼續開展逆反射動態測試的相關試驗。